Көп айнымалы функциялар: анықталу облысы, шегі мен үзіліссіздігі, дербес туындылар және толық пен жоғары ретті дифференциалдар



Көп айнымалы функция туралы түсінік. Екі айнымалы функцияның шегі, үзіліссіздігі. Көп айнымалы функцияның дербес туындылары. Көп айнымалы күрделі функцияның туындысы. Көп айнымалы функцияның толық дифференциалы. Жоғары ретті дифференциалдар

Анықтама. Егер x, y, z, . . . , t айнымалылардың әрбір n мәндер жиынтығына w айнымалысының бір мәні сәйкес қойылса, онда w тәуелсіз n айнымалыдан функция деп аталады да, былай белгіленеді: w=F(x, y, z, . . . , t)
Үш не одан да көп айнымалылардың функцияларының графиктерін кескіндеудің геометриялық мағынасы болмайды.
Көп айнымалы функция туралы түсінік
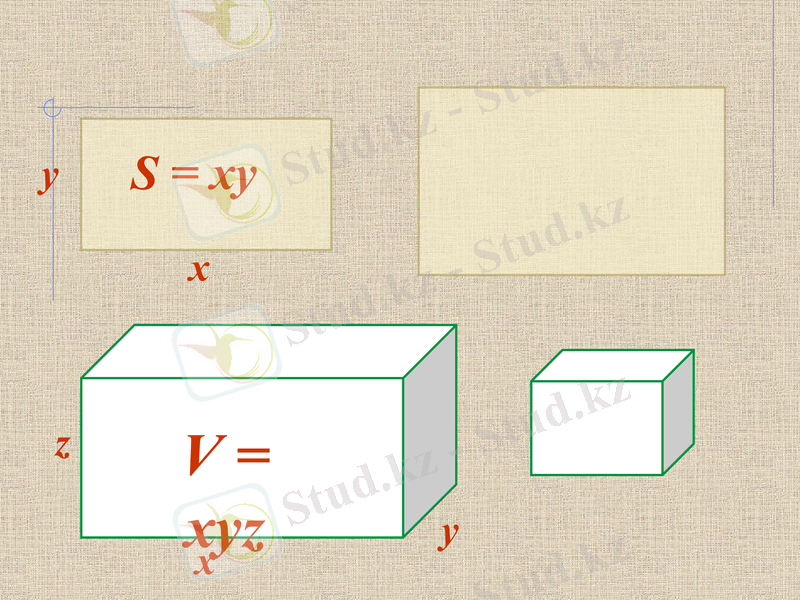
y
x
S = xy
z
x
y
V = xyz

Анықтама. Егер D облысына тиісті x және y тәуелсіз айнымалы шамалардан құралған әрбір ( х, у) жұбы үшін f арқылы z шамасының анық бір мәні сәйкес қойылса, онда z шамасы D облысында анықталған екі тәуелсіз x және y айнымалыдан функция деп аталады және z=f(x, y) түрінде белгіленеді.
Анықтама. z=f(x, y) функциясының мәндері анықталатын x және y мәндерінен тұратын (х, у) жұптарының жиынтығы осы функцияның анықталу облысы немесе бар болу облысы деп аталады.
Екі айнымалы функция және анықталу облысы
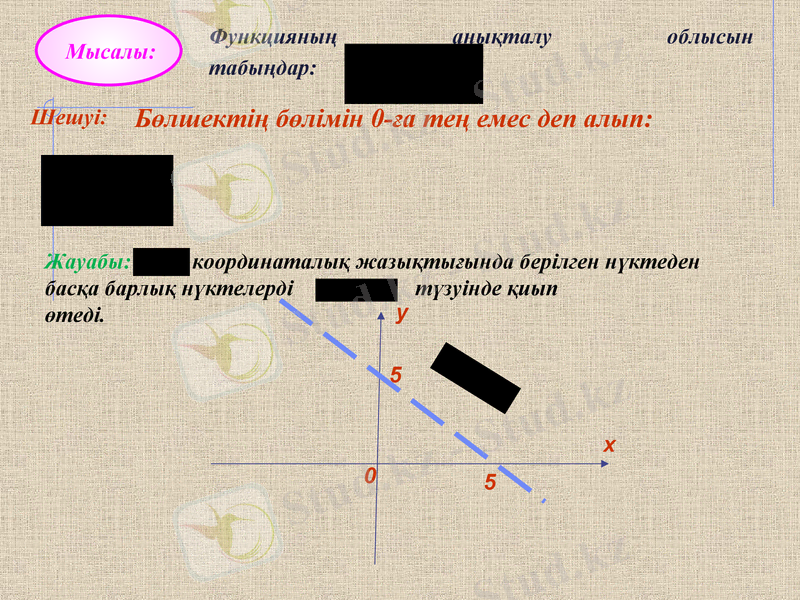
Функцияның анықталу облысын табыңдар:
Шешуі:
Бөлшектің бөлімін 0-ға тең емес деп алып:
Жауабы: координаталық жазықтығында берілген нүктеден басқа барлық нүктелерді түзуінде қиып өтеді.
y
x
5
5
0
Мысалы:

Функцияның анықталу облысын табыңдар:
Шешуі:
Түбірдің астындағы таңба теріс болмауы керек :
Жауабы: жарты жазықтық
у
x
y =
Мысалы:

Функцияның анықталу облысын табыңдар және оның суретін салып көрсетіңдер:
Шешуі:
Түбірдің астындағы таңба теріс болмауы керек:
және, бөлгіш нөлге тең болмайтынын ескере отырып, теңсіздік қатаң болып табылады:
теңдеуі шеңбер болып табылады. Радиусы, координаталық жазықтықты екі бөлікке бөледі- «ішкі» және «сыртқы» шеңберге.
Теңсіздік қатаң болғандықтан, шеңбердің өзі функцияның анықталу облысына кірмейді және сондықтан оны үзік сызықтармен сызу қажет.
Мысалы:
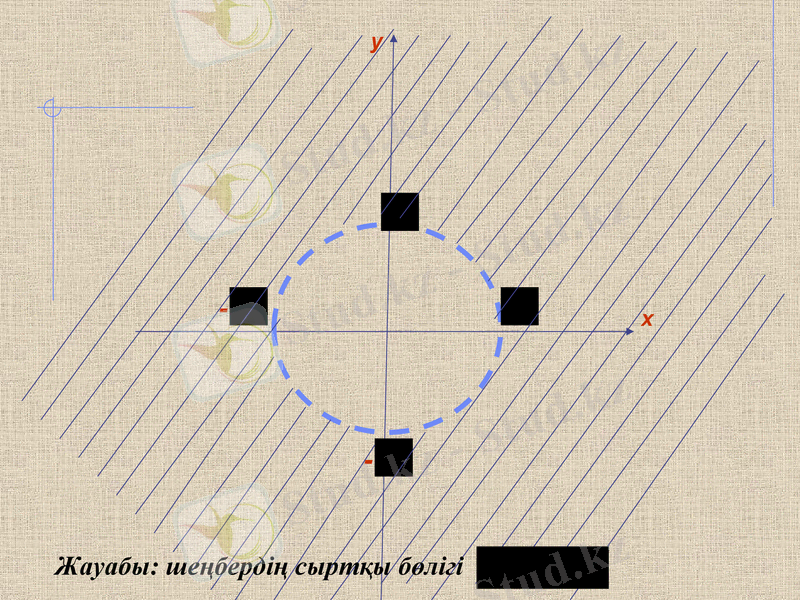
y
x
-
-
Жауабы: шеңбердің сыртқы бөлігі

Оху жазықтығының G облысында анықталған және Охуz тік бұрышты декарттық координаталар жүйесі.
функциясын қарастырайық,
х
у
z
z=f(x, y)
P
O
х
у
G
Нәтижесінде кеңістікте Р нүктесін және х, у, z = f(x, y) координаталарын аламыз.
Көп айнымалы функцияның геометриялық кескіні

Анықтама. Р нүктесінің геометриялық орны функциясының теңдеуінің координаталарын қанағаттандыратын болса, онда ол екі айнымалыдан z= f (x, y) функциясының геометриялық кескіні деп аталады.
Айналу параболоиды
Екі айнымалыдан z= f (x, y) функциясының геометриялық кескіні (графигі) Oxyz кеңістігіндегі бет болып табылады.

Анықтама. M0(x0, y0) нүктесінің радиусы r маңайы деп, координаталары мына теңсіздікті қанағаттандыратын жазықтықтың барлық М (х, у) нүктелерінің жиынын айтады, яғни бұл нүктелер центрі M0(x0, y0) нүктесінде радусы r болатын шеңберге тиісті нүктелер.
Енді Oxy жазықтығының G облысында анықталған z=(х, у) функциясы берілсін және M0(x0, y0) нүктесі осы G облысының ішкі немесе шекаралық нүктесі болсын.
Көп айнымалы функцияның шегі мен үзіліссіздігі

Ескерту: Бұл жерде екі айнымалыдан функцияның шегі М(х, у) нүктесі M0(x0, y0) нүктесіне қалай (қандай сызықтың бойымен) ұмтылуынан тәуелсіз болатынын ескеруіміз керек.

Анықтама. M0(x0, y0) нүктесі f(x, y) функциясының анықталу облысына тиісті болсын. Егер келесі теңдік
орындалса, онда z = f(x, y) функциясы M0(x0, y0) нүктесінде үзіліссіз деп аталады және М(х, у) нүктесі M0(x0, y0) функцияның анықталу облысында қала отырып, кез-келген жолмен ұмтылады.
Осы анықтамадан функция нүктеде үзіліссіз болу үшін келесі
шарттардың орындалуы қажет екендігі шығады:
z = f(x, y) функциясы M0(x0, y0) нүктесінде анықталған;
шегі бар;
Функцияның шегі оның сол нүктедегі мәніне тең:

Функцияның үзіліс нүктесін есепте:
Шешуі: (0; 2) нүктесі функциясында анықталады, олай болса функцияның осы нүктелеріндегі мәнін есептеуге болады. Онда функцияны шешуге мына теңсіздікті қолданамыз:
Сонда:
Мысалы:

Функцияның үзіліс нүктесін есепте:
Шешуі: (0; 3) нүктелері функцияның анықталу облысына кірмейді, онда х = 0 болғанда 0/0 анықталмағандығына келеді. Сондықтан алымында, бөлімінде у-ке көбейтіп бөлеміз және u = xy ауыстыруын жасаймыз.
Сонда:
Мысалы:
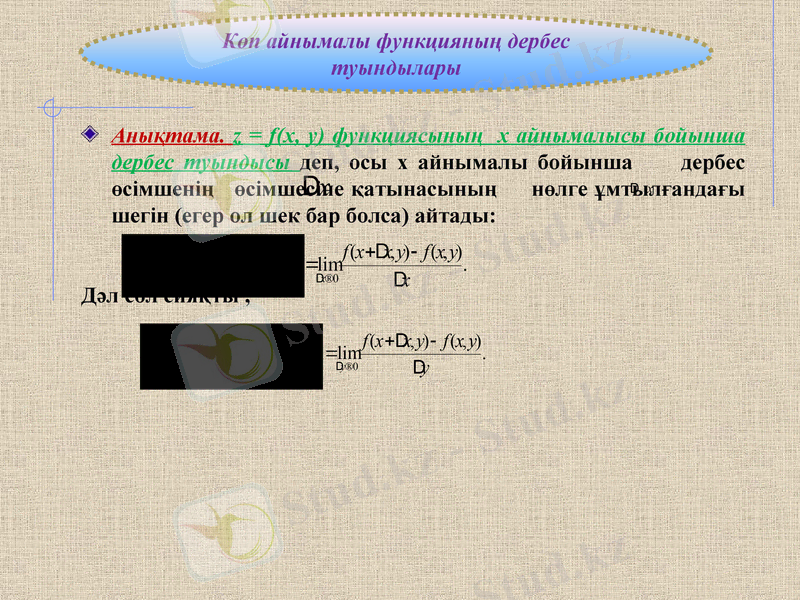
Анықтама. z = f(x, y) функциясының x айнымалысы бойынша дербес туындысы деп, осы x айнымалы бойынша дербес өсімшенің өсімшесіне қатынасының нөлге ұмтылғандағы шегін (егер ол шек бар болса) айтады:
Дәл сол сияқты,
Көп айнымалы функцияның дербес туындылары

Функцияның дербес туындыларын табыңдар:
1)
Шешуі: Дербес туындысын у мәні бекітілген (өзгермейтін) деп алып есептейік:
Ал есептегенде х мәні өзгермейді деп аламыз:
2)
Шешуі: Бұл функцияның х аргументі бойынша дербес туындысын есептеген кезде, оны тек осы бір ғана х айнымалыдан тәуелді деп есептейміз, яғни, у мәні өзгермейді. Осы кезде функциясы х аргументіне тәуелді дәрежелік функция болады, яғни . Бұдан бізге белгілі формула бойынша . Осылайша талқылай отырып, дербес туындысын көрсеткіштік функциясынан аламыз. Сонда .
Мысалы:

функциялары берілсін, сонда функциясы x, у аргументтерінен тәуелді күрделі функция болады. Берілген функциялары өз аргументтері бойынша дифференциалданатын функциялар. Мына дербес туындыларды есептейік:
x аргументіне өсімшесін берейік те, y аргументін өзгеріссіз қалдырайық, сонда u, v функциялары сәйкес өсімшелерін, ал z = f(u, v) функциясы өсімшесін алады:
Соңғы теіңдіктің екі жағын да -ке бөліп мынаны аламыз:
Егер онда себебі u, v үзіліссіз функциялар, және та
орындалады. Осыларды ескере отырып шекке көшсек
Осылайша, х-ті өзгеріссіз қалдырып у-ке өсімше берілсе
аламыз.
Көп айнымалы күрделі функцияның туындысы

Төмендегі функцияның дербес туындыларын табыңдар:
Шешуі:
Мысалы:

функциялары берілсін. Осы күрделі функциясынан толық дифференциал алайық:
бірақ
сондықтан
немесе
Осы жерде біз КАФ толық дифференциалының өрнегі (бірінші ретті дифференциал) u, v - тәуелсіз айнымалы немесе тәуелсіз айнымалылардан функция болғанына қарамастан бірдей түрде жазылатынын көрсеттік. Бұл бірінші ретті дифференциал түрінің инварианттығы деп аталады.
Көп айнымалы функцияның толық дифференциалы

Берілген
функциясы бойынша оның толық дифференциалы dz-ті табу керек.
Шешуі: Дербес туындылар:
демек,
2. функциясы берілген. dz- ті табу керек.
Шешуі:
болғандықтан,
Мысалы:

z = f(x, y) функциясының бірінші ретті дифференциалы - функцияның толық өсімшесінің аргументтер өсімшелеріне қатысты сызықты бөлігі аталады:
z=f(x, y) функциясының II ретті дифференциалы оның I ретті дифференциалынан x, y айнымалыларының функциясы ретінде (dx, dy бекітілген мәндерінде) алынған дифференциал, яғни:
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz