Бастауыш сыныпта теңдеулерді оқыту әдістемесі

Теңдеуді оқыту әдістемесі

Орындаған:Қанапия А.

Кіріспе

Болашақтың бүгіннен де нұрлы болуына ықпал етіп, адамзат қоғамын алға апаратын күш тек білімде ғана. Ал бастауыш сынып оқушыларының білуге деген ынтасы мен мүмкіндіктерін оқу үрдісінде үздіксіз пайдаланып отыру және сабақ барысында алған білімдерін тәжірибеде қолдану дағдыларын қалыптастыру үшін алгебра элементтерін оқытудың маңызы зор.

Бастауыш математика курсы бағдарламасында алгебра элементтерінің ішінде дидактикалық тұрғыдан алғанда аса маңыздысы - теңдеу жайында түсінік беру және оны шешудің тәсілдерін оқытып, үйрету, сондай-ақ есепті алгебралық тәсілмен (теңдеудің көмегімен) шешудің мән-мағынасын ашу болып табылады.

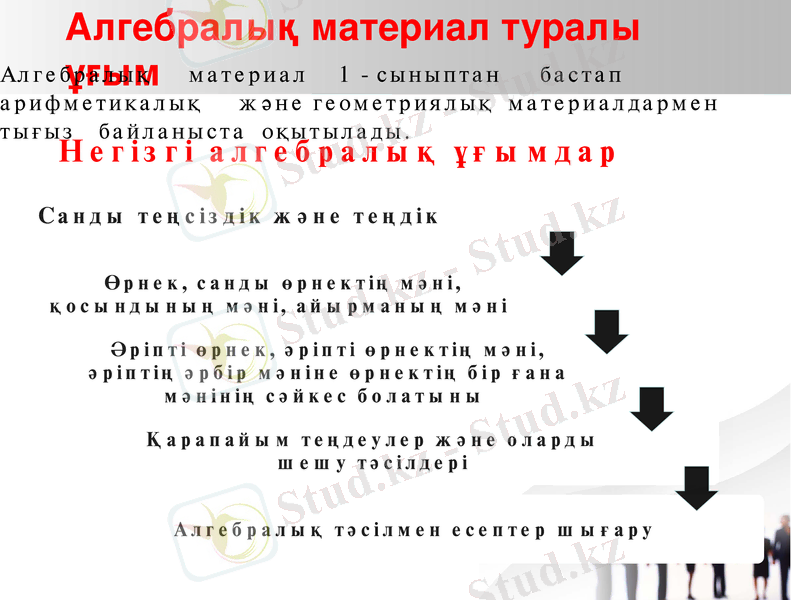
Негізгі алгебралық ұғымдар

Алгебралық материал туралы ұғым

Алгебралық материал 1 - сыныптан бастап арифметикалық және геометриялық материалдармен тығыз байланыста оқытылады.

Теңдеу деп құрамында әріп болатын және онымен белгіленген санды іздеу мақсаты қойылатын теңдікті айтады. Белгісіз санның теңдеуді тура санды теңдікке айналдыратын мәнін теңдеудің түбірі деп атайды.

Теңдеуді шешу дегеніміз оның түбірлерін табу.

1-сыныпта х-2=8, 10-х=4

2-сыныпта х-3=10+5

3-сыныпта х·3=12, 5·х=10, 6:х=3

4-сыныпта 96:х=3, у-230=110+265, 5×х=150:3, 60×у=900-420 түрдегі күрделі теңдеулер енгізіледі.

Теңдеумен танысу дерексіз сандармен берілген есептерді шығарғанда болады, мысалы мынадай: «Белгісіз санға 3-ті қосып, 8 алған. Белгісіз санды табу керек». Осы есеп бойынша белгісіз саны бар мысал құрастырылады, оны былай жазуға болады +3=8. Содан кейін мұғалім математикадан белгісіз сан латын әріптерімен белгіленеді деп түсіндіреді. Бір әріптің мысалы х (икс) әрпінің жазылуы және оқылуы беріледі. Белгісіз санды әріппен белгілеу және мысалды оқу ұсынылады. Мынадай мысалдарды шығаруды үйрену мақсаты қойылады.

х+3=8

х=8-3

х=5

Теңдеуді шешудің тәсілдері

Теңдеу шешудің бірінші тәсілі «сынап көру» 1-сыныпта қарастырылады. а әріпінің орнына тура санды теңдік шыққанша, сандарды кезекпен қойып көреді.

Мысалы:

демек, а=4 - теңдеудің

шешімі.

Екінші тәсілі теңдеуді теңбе-тең түрлендіруге негізделген:

х+2=5

х+5=5 - теңдеудің екі бөлігінен де бірдей санды азайту;

х=5-2 - теңдеудің екі бөлігінен де 2-ні азайтамыз

х=3

Тексеру:

3+2=5

5=5

Теңдеудің шешуін тексергенде х-тің орнына оның мәні қойылады, егер теңдеудің сол бөлігіндегі санды өрнектің мәні оның оң бөлігіндегі санға тең болса, онда теңдеу дұрыс шешілген.

Теңдеуді шешудің үшінші тәсілінде қосу мен азайтудың, көбейту мен бөлудің өзара кері амалдар екендігі пайдаланылады:

57-х=7, санынан х-ті азайту дегеніміз х-ке қандай санды қосқанда, 57 шығады деген сөз. Ондай сан 7, ендеше х+7=57, осылайша таныс тәсілге, яғни екі бөлігінен де бірдей санды азайтуға келтіріледі, ол сан - 7,

х+7=57

х=57-7

х=50

Тексеру:

50+7=57

57=57

Есепті теңдеу құру арқылы шығару

Алгебралық тәсілмен шығарылатын есептің ең бір қиын кезеңі теңдеу құру болып табылады.

Осы мақсатта дерексіз сандармен берілген есептерді ұсыну тиімді. Осы кезеңде мына сияқты есептерді қарастыруға болады.

1. Егер белгісіз санды 26-ке арттырса, онда 725 шығады. Белгісіз санды табыңдар. (М-4, 14-б. )

Келесі кезеңде арифметикалық амалдардың белгісіз компоненттерін табуға байланысты есептер теңдеудің жәрдемімен шығарылады.

M. 1. Жәшікте бірнеше килограмм алма болды. Жәшіктен 8 кг алма алынғаннан кейін онда тағы 13 килограмм алма қалды. Бастапқыда жәшіктер неше килограмм алма болған? (М-4, 152б. )

Бұл кезеңде арифметикалық амалдың компоненті мен нәтижесінің санды өрнек түрінде болып келуіне байланысты теңдеулер құруға есептер ұсынылады. Мұнда құрама есепті теңдеу жәрдемімен шығарудың мүмкіндігі көрсетіледі.

1. 643 пен белгісіз санның айырмасы 585 пен 5-тің бөліндісіне тең. (М-4, 88-89б. )

2. 1200 бен ойлаған санның айырмасы 18 бен 6-ның көбейтіндісіне тең. Ойлаған санды тап. (М-4, 88-89б. )

Енді теңдеу құруға мүмкін болатын мәтінді құрама есептер қарастырылады. Оларды шығару барысында алгебралық тәсілді енгізу қажеттігін және оның мәнді ерекшелігі мен артықшылығын нақты көрсетіп беруге болады.

Ұқсас жұмыстар

Бастауыш сыныпта әріпті өрнектер мен теңдеулерді оқыту әдістемелері

Бастауыш сыныпта дүниетану сабағын өткізу әдістемесі

Бастауыш сыныпта қазақ тілінен етістікті оқытудың әдістемесі

Бастауыш сыныпта сан есімді оқыту әдістемесі: психопедагогикалық ерекшеліктері және жалғаулар мен жұрнақтардың маңызы

Мұхтар Шаханов шығармашылығы мен Желтоқсан оқиғасын бастауыш сыныпта оқыту әдістемесі

Бастауыш мектеп математикасындағы алгебралық ұғымдар мен оларды оқыту әдістемесі

2-сыныпта 20-ға дейінгі сандарды оқыту әдістемесі

Бастауыш сыныпта математиканы сын тұрғысынан ойлау технологиясы арқылы оқыту

Бастауыш сыныптарда ойын арқылы оқыту әдістемесі

Бастауыш сыныпта Ыбырай Алтынсарин шығармаларын оқыту: теориялық негіздер мен әдістемелік сабақ жүйесі

Пәндер