Симметрия топтары

Презентация қосу

Халықаралық Қазақ –
Түрік университеті
Буланбаева Бахытнур ЖФЗ - 011
\

Симметрия топтары
Класс немесе симметрия түрлері деп көпжақты кристаллдарда
кездесетін толық симметрия элементтері тобын айтады. Көпжақты
кристаллдардағы барлық симметрия элементтері бір-бірімен өзара
байланыста болады. Бір симметрия элементінің екінші симметрия
элементіне тәуелділігінен және кристаллдарда бесінші және
алтыншы реттен жоғары симметрия осьтерінің болмағандығынан,
көпжақты кристаллдарда кездесетін симметрия элементтер тобының
саны шектелген болады. Симметрия элементтерінің мүмкін болған
комбинация топтарының саны 32 тең екендігі анықталған. Басқаша
айтқанда, 32 кристаллографиялық класс немесе симметрия түрі бар
(2 кесте). 32 симметрия классының болуын 1830 жылы И.Гессель,
кейін Гессельден тәуелсіз 1867 жылы орыс академигі А.В.Гадолин
математика жолымен қорытып тапқан. 2 кестеде класстарды белгілеу
түрлері және симметрия класстарының атаулары көрсетілген.
Әрбір симметрия классына симметрия элемент топтары негізінде
кристаллдар топтасқан немесе бір симметрия элементі бар, басқа симметрия
элементі жоқ кристаллдар топтасқан.
Симметрия формуласы берілген кристаллдың барлық симметрия
элементтеріне жазылған. Бірінші орында жоғарыдан төмен симметрия осі,
екінші орында симметрия жазықтығы, ары қарай симметрия орталығын
(мысалы, тетрагональды призмаға – L44 L25РС) жазу қалыптасқан.
Симметрия классын анықтау үшін алдымен екі немесе үш симметрия
элементін алады (симметрия элементін тудыратын), содан кейін қалған басқа
симметрия элементін табады.
Әрбір симметрия классы белгілі симметрия элементіне сәйкес өздерінің
аттары бар. Қарапайым класс тек бас симметрия осіне ие; егер сонымен
қатар симметрия орталығына ие болса, онда классты орталық деп атайды.
Егер көпжақты кристаллдарда симметрия осімен қатар симметрия
жазықтығы болса, онда планальды класс деп атайды (грек тілінде планум
деген сөз жазықтық деген мағынаны береді). Аксиальды симметрия классы
әр түрлі ретті бірнеше симметрия осіне ие (грек тілінде аксон деген сөз ось
деген мағынаны береді). Мүмкін болған максимальды осьтер жазықтықтар
симметриясына ие. Сонымен қатар симметрия орталығы болса, ондай
симметрия классын планаксиальды деп атайды. Егер кристаллда
инверсионды – қарапайым (тек ) немесе инверсион-планальды ( және Р)
симметрия классы деп атайды.
Бірлік және симметриялық эквивалентті
бағыттар

Бірлік бағыт деп кристаллда бір ғана басқа қайталанбайтын бағыттың
болуын айтады. Мысалы, алтыжақты призмадағы немесе призмадағы 6
ось, төртжақты призмадағы немесе пирамидадағы 4 ось бірлік бағытқа
жатады.
Сонымен қатар, кубтағы немесе октаэдрдегі 4 ось бірлік бағыт емес,
мұндай осьтер бұл жерде үшеу. Көрсетілген бұл үш ось кубтың кез-келген
симметрия жазықтығына шағылу көрінісі арқылы бір-біріне
сәйкестендіруге болады. Симметрия элементімен байланысқан
кристаллдағы қайталанатын бағыттарды симметриялы тең немесе
эквивалентті бағыттар деп аталады.
Кубта және октаэдрде бірлік бағыт жоқ, оларда симметриялы
эквивалентті бағыттар бар. Симметрия элементі жоқ немесе симметрия
орталығы бар көпжақты кристаллдарда әрбір бағыт бірлік бағыт болып
қайталанбайтын бағыт болады, мұнда симметриялы тең (эквивалентті)
бағыт болмайды.
Кристаллографиялық категориялар,
сингониялар

Симметриясымен және бірлік бағыт санымен кристаллдар үш
категорияға бөлінеді: жоғары, орта және төмен. Басқаша айтқанда
сәйкесінше a=b=c; a=b≠c; a≠b≠c кристалдар. Жоғары категориялық
кристаллдарда бірлік бағыттары болмайды, бірақ бұларда бірнеше
симметриялы – эквивалентті бағыттар болады, олар екіден жоғары
осьтерде бір-біріне сәйкес келеді. Бұл бағыттарда кристаллдың
қасиеттері бірдей болады, сондықтан жоғарғы категориядағы
кристаллдарда анизотропиялық қасиет жоқтың қасы. Жоғары
категориялы кристаллдардың жылу өткізгіштік, электр өткізгіштік,
сыну көрсеткіші сияқты физикалық қасиеттері изотропты, ал
серпімділігі, электрооптикалық, физикалық қасиеттерінің
анизотроптылығы басқа категориядағы кристаллдардың
анизотроптылығынан әлдеқайда төмен. Кристаллдың сыртқы
көрінісі изо, метрлі, мысалы куб, октаэдр, тетраэдр.
Орта категориядағы кристаллдар жоғары ретті (3, 4, 6, , )
осьтеріне бағыттас бір бірлік бағытқа ие. Бұл кристаллдардың
анизотропиялық физикалық қасиеттері жоғары категориядағы
кристаллдардың анизотропиялық қасиеттеріне қарағанда
жоғары. Әсіресе кристаллдың бас симметрия бойы және оған
көлденең бағыттағы анизотропия қасиеті елеулі айқын көрінеді.
Орта категориядағы кристаллдардың сыртқы көрінісі призма,
пирамида және т.б. болады.
Төменгі категориядағы кристаллдарда екінші ретті симметрия
осінен жоғары симметрия осі болмайды, ал бірлік бағыттар
бірнеше болады. Бұл кристаллдардың анизотроптық қасиеті өте
жоғары болады, кристаллдың сыртқы көрінісі ең төменгі
симметрияда болады
3 категория 7 сингонияға бөлінеді (сингония грек тілінде
бұрыш-сәйкестік-сходноугольность мағынасын береді). Бір
сингонияға бірнеше топтар бірігеді, ол біріккен топтарда
бірлік бағыт саны бірдей болып, ұқсас симметрия элементтері
бір немесе бірнеше болады. Көпжақты кристаллдарды
математикалық түрде сипаттау үшін, әрбір сингония өзінің
қарапайым (элементар) параллелепипедпен сипатталады.
Әрбір элементар параллелепипед (4 суретке қара) элементар
ұяшығы бір-біріне тең а, в, с үш осьтік сызықпен және , ,
координата осьтер арасындағы бұрыштармен сипатталады.
Кристаллографияда әр уақытта оң координата жүйесін
қолданады, жалпы жағдайда тік бұрышты емес координата осі
бойынша бір-біріне тең емес (а в в) сызық қолданылады. а, в,
с,
, , шамалар кристаллдың метрикасы болып есептеледі
және оларды кристалл торының параметрлері немесе
периодтары деп аталады
Сонымен, сингония бойынша кристаллдарды
классификациялау үшін кристаллографиялық координата
жүйесін таңдау арқылы анықталады, яғни түрлерге
бөлінеді екен, яғни кристаллдың элементар ұяшығын
таңдау (анықтау) арқылы бөлінеді.
Кристаллдарды мұндай классификацияға бөлудің себебі,
симметрия элементтер түрі кристаллдың ішкі
құрылымына тәуелді, ал әрбір кристаллдың ішкі
құрылымы элементар ұяшыққа және олардың
параметріне тәуелді.
Кристаллдардың қарапайым
формалары және
олардың комбинациялары
Әрбір кристалл белгілі симметрия элементтер комплексімен
сипатталады. Сонымен қатар кристаллдардың формасы әр түрлі
болып, олардың симметрия элементтері бірдей болуы мүмкін, мысалы,
куб және октаэдрлерде (3L4 4L3 6L2 9PC). Көпжақты кристаллдарды
жан-жақты сипаттайтын мәліметтерді бірнеше сипаттайтын типке
келтіру, көпжақты кристаллдарды сипаттауға жеңілдік тудырады.
Әлемде белгілі кристаллдарды, (барлығы~104 жуық кристаллдарды) 47
түрлерге бөліп сипаттайды (90-сурет). Кристаллдың сыртқы көрінісі
деп (кристаллдың габитусы) сол кристаллдық жақтар қосындысын
айтады. Бұл жақтарды симметриялы бір-біріне тең жақтар топтарына
бөлуге болады. Бір жақтан симметриялық өңдеу арқылы алынған
жақтар тобын қарапайым форма деп атайды. Қарапайым форманың
жақтары симметриялы теңдігі тек геометриялық формасымен ғана
емес, олар физикалық және химиялық қасиеттерімен де тең.
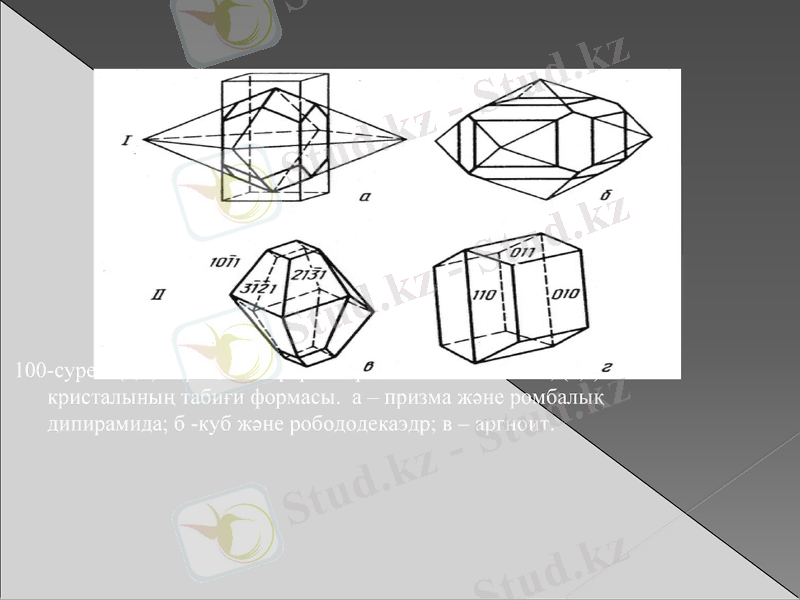
100-сурет. (а,б) қарапайым формалардың комбинациясы, (в,г)
кристалының табиғи формасы. а – призма және ромбалық
дипирамида; б -куб және робододекаэдр; в – аргноит.
Егер кристалл бірнеше жақтар түрінен құралған болса, онда ол кристаллдың
сыртқы формасы бірнеше қарапайым формалардың комбинацияларынан
құралған болады. Екі немесе бірнеше қарапайым формалар симметрия
элементтері арқылы қосылса, оны комбинация деп атайды.
Қарапайым формалар ашық және жабық болады.
Егер қарапайым форманың жақ топтары кеңістікті жаппаса, онда оны ашық
деп атайды; егер кеңістікті жапса – жабық форма деп атайды. Ашық
қарапайым форма тек қарапайым формалар комбинациясын құрайтын басқа
қарапайым формалармен бірге кристаллда кездеседі.
Қарапайым форма деп аталуы грек тіліндегі сан (моно – бір, ди – екі, три –
үш, тетра – төрт, окта – сегіз, дека – он, додека – он екі) сөз (эдра – жақ,
пинакс – тақтай, скаленос – қисық, тегіс емес, тропеци – стол) түбірінен
шыққан атаулар.
Ашық қарапайым формаға мыналар жатады: моноэдрлер (34), пинакоид (32),
диэдр (31), призмалар (15-21) және пирамидалар (1-7). Жабық қарапайым
формаға дипирамидалар (8-14)
Геометриялық
кристаллографияның заңдары
Кристаллография нақты ғылым саласы болып
қалыптасуы кристаллдардың сыртқы формасын
зерттеуден басталған. Формасының сыртқы көрінісін
көру, яғни жазық жақтарын, олардың арасындағы
бұрыштарын және байқалған олардың арасындағы
заңдылықтарды зерттеу кристаллдың ішкі құрылымының
идеал екендігіне дәл көз жеткізуге мүмкіндік берді.
Кристалл жақтарының және олардың қырларының өзара
орналасу заңдары кеңістік торларының бар екендігінің
макроскопиялық көрінісі екендігіне алып келді.
Кеңістік бұрыштарының заңы

Кристаллдардың шектелуін бірінші олардың жазық жақтарының
болуымен сипатталады. Белгілі заттың кристаллы әр түрлі түрде
болуы мүмкін, бірақ міндетті түрде оларда көп кездесетін жақтарды
ажыратуға болады. Егер бір заттың бірнеше кристаллдарын
қарастырсақ, онда олардың кейбір жақтары бір-біріне параллель
екендігін көреміз, бұл жақтарды кристаллдың сәйкестік жақтары
деп атайды.
Бұрыштардың тұрақтылығы заңы мынадай дейді:
Термодинамикалық тұрақты шартта (T=const, P=const) берілген
кристаллдық сәйкестік жақтар арасындағы бұрыш тұрақты.
Кристалл жақтарының өлшемдері олардың формалары
кристаллизация шартына байланысты әр түрлі болуы мүмкін, бірақ
әрбір затың сәйкестік жақтары арасындағы бұрыштар еш уақытта
өзгермейді
Көптеген кристаллдар бұрыштарының тұрақтылығы минуттың бір
бөлігіне дейін үлкен дәлдікпен сақталады. Кристаллдың химиялық
құрылымының ауытқуы, қоспа атомдардың болуы және т.б., сонымен
қатар сыртқы әсерлер бұрыштарды елеусіз шамаға өзгертуі мүмкін.
Кристалл бұрыштарының тұрақты болуының себебі, бір заттың
барлық кристаллдар құрылымы бірдей болуынан келіп шығады. Бір
заттың әр түрлі кристаллдарының сәйкестік жақтары, құрылымы да
бірдей жазық торға ие болып, олар бірдей бұрышты тудыруы керек.
Бұл кристаллографиядағы негізгі заңды 1669 жылы дат минерологы
Н.Стенон, бірнеше кварц кристаллдарды зерттеп және айтқан
қорытындыларын жүз жылға жақын аралықтарда ұмтылып, бір-
бірінен тәуелсіз 1749 жылы М.В.Ломоносов және 1783 жылы Ромэ-
Делия қайтадан ашты. Сондықтан бұрыштың тұрақтылық заңын көп
жағдайда Стенон-Ломоносов-Роме-Делия ашты деп айтуға болады.
Сондықтан бұрыштық тұрақтылық заңын көп жағдайда Стенон-
Ломоносов-Роме-Делия заңы деп атайды.
Кристаллдық сәйкестік арасындағы бұрыш кристаллды сипаттайтын
болғандықтан, белгісіз кристаллды олардың бұрышын белгілі кристаллдардың
бұрыштарымен салыстыра отырып, белгісіз кристаллды анықтауға мүмкіндік
береді. Бұл жағдай, 1910-1919 жылдары орыс кристаллогрофы Е.С.Федоровтың
басшылығымен жасалған арнайы тәсілі практикада қолдануға мүмкіндік
тудырды.
Кристалл жақтары арасындағы бұрыштарды арнайы гониометрлер
қондырғылары арқылы өлшейді (грек тілінде «гониа» деген сөз бұрыш деген
мағынаны береді), ганиометр қондырғыларының түрлері: шағылдыратын-
прикладты, шеңберлі және екішеңберлі ганиометрлер.
Көпжақты кристаллдардың симметриясы және формасы туралы зерттеулер
бірінші міндетті түрде ганиометр өлшеулері нәтижелеріне негізделген.
Қазіргі кезде кристалл жақтары арасындағы бұрыштарды рентген сәулесі
арқылы алынған рентгенограмма арқылы өлшейді. Мұнда өлшеулерге
ганиометриялық өлшеудегі сияқты тура жақты кристаллдың қажеті жоқ, тек
зерттелетін заттың ұнтақтары болса жеткілікті
Параметрлер қатынастары заңдарының
рационалдығы (бүтін сан заңы)

1784 жылы француз кристаллогрофы Аббат Р.Гаюи
параметрлер қатынас заңының рационалдығын ашты,
мұны Гаюи заңы деп атайды. Әрбір кристалл зат
жақтарының кеңістікте орналасуын рационалды
қатынастан алынған сандар арқылы сипаттау мүмкін
екендігін анықтады.
Егер бір «О» нүктеде қиылысатын кристаллдың үш
компленарлы емес қабырғаларын координата осьтері
ретінде алсақ, онда ол қабырғалармен (x, y, z) қиылысатын
кез-келген параметр деп аталатын екі жақтың бір-біріне
қатынасы бүтін санның қатынасындай болады
Шынында да, Р1Р2Р3 жақ үш ОР1, ОР2 және ОР3 параметрлерімен
сипатталады, ал Р 1Р 2Р
3 және ОР 1, ОР 2, ОР
3 параметрлермен
сипатталады. Бір жақтың параметрін екінші жақтың параметріне
бөлсек, мынаны аламыз:
ОР1 /ОР 1, ОР2 /ОР 2, ОР3 /ОР 3 =p : q : r, мұндағы p, q және r бүтін
сандар және аса үлкен сандар емес. Сонымен, Гаюи заңы былай
оқылады: үш компленарлы емес кристаллдың кез-келген екі
қабырғасын қиятын екі параметрдің қатынасы бүтін сандардың
қатынасына тең және бұл сандар аса үлкен емес.

Ұқсас жұмыстар

Дұрыс көпжақтардың симметриясы

Осьтік симметрия

Поэзиядағы симметрия

Медициналық гельминтология өзекті мәселелер

Осьтік және центрлік симметрия

Кристаллохимия

САЛУ ЕСЕПТЕРІН ШЕШУ ӘДІСТЕМЕСІ

КОСТЮМ КОМПОЗИЦИЯСЫ

Күн жүйесі планеталары қозғалысының заңдары

Инерция моменті Инерция тензоры

Пәндер