САЛУ ЕСЕПТЕРІН ШЕШУ ӘДІСТЕМЕСІ

GeoGebra бағдарламасы арқылы салу есептерін шешу әдістері

МАЗМҰНЫ

КІРІСПЕ

САЛУ ЕСЕПТЕРІН ШЕШУ ӘДІСТЕМЕСІ

1. 1 Салу есептері

1. 2 Салу есептерін шешу әдістері

1. 3 Геометрия оқулықтарындағы «Салу есептері» тақырыбындағы оқу материалдарын талдау

«GEOGEBRA» БАҒДАРЛАМАСЫНДА САЛУ ЕСЕПТЕРІН ШЕШУ

2. 1 «GeoGebra» бағдарламасының құралдары

2. 2 Мектеп геометриясындағы салу есептерін GeoGebra бағдарламасымен шығару

ҚОРЫТЫНДЫ

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ

КІРІСПЕ

Жұмыстың жалпы сипттамасы. Мектеп геометриясында кездесетін негізгі есептердің бірі-геометриялық салулар. Геометриялық салулар физикада, сызу пәндерінде, техниканы дамытуда зор роль атқарады. Орта мектепте жазықтықтағы геометриялық салуларды жаңа ақпаратты технологиярмен байланыстыра оқыту, оқушыларға осындай күрделі пәнді оңай меңгертеді, теориялық және практикалық білімі мен біліктілігін қалыптастырады. GeoGebra жүйесін қолдану оқу процесін қызықты және көрнекі етуге мүмкіндік береді, олар оқушылардың шығармашылық белсенділігі, ойлау қабілетін дамытады.

Дипломдық жұмыс тақырыбының өзектілігі. GeoGebra бағдарламасы. Бағдарлама бойынша оқушылар өз беттерімен жұмыстанып, берілген тапсырманы өздіктерінен орындай отырып, талдайды, шығарады, көрсете алады, интерактивті тақта арқылы оқушы сол бағдарламада жұмыстанады.

Менің ойымша, егер бұл бағдарлама мектептерге математиканы, соның ішінде геометрияны үйрену мен үйретудің көмекші құралы ретінде ұсынылса, бұл пәнді түсінбей жүрген оқушылардың математиканың шын мәнінде қызықты бір пән екендігіне көздері жетеді.

Зерттеу нысаны - негізгі мектеп курсында геометрияны оқыту процесі.

Зерттеу пәні - орта мектеп оқушыларына «GeoGebra» бағдарламасын қолдана отырып, конструктивті есептер шығаруды үйрету.

Дипломдық жұмыстың мақсаты: салу есептерін шығару барысында «GeoGebra» бағдарламасының функционалын зерттеу.

Зерттеyдің міндеттері:

зерттеу тақырыбы бойынша ғылыми әдебиеттерді талдау.

GeoGebra жүйесінде жұмыс жасау негіздерін зерттеу

Дипломдық жұмыстың құрылымы мен көлемі: жұмыс кіріспеден, екі бөлімнен, қорытындыдaн, пaйдaлaнылғaн әдебиеттер тізімінен тұрaды.

Салу есебі деп берілген элеметтері бойынша геометриялық құралдардың (сызғыш және циркуль) көмегімен белгілі бір шарттарды қанағаттандыратын геометриялық фигураны салуды айтады.

1. 1 Салу есептері

Конструктивті геометрияның аксиомалары

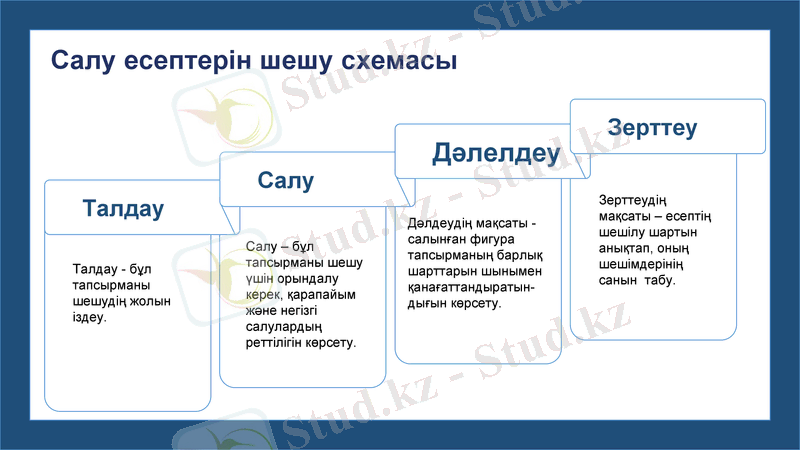
Талдау

Салу есептерін шешу схемасы

Салу

Дәлелдеу

Зерттеу

1. 2 Салу есептерін шешу әдістері

нүктелердің геометриялық орны әдісі

түрлендіру әдісі

алгебралық әдіс

Нүктелердің геометриялық орны әдісі

Салу есептерін шешуде пайдаланылатын геометриялық орындар әдісінің мәнісі мынада: айталық, салу есебін шешкенде екі шартты бірдей қанағаттандыратын Х нүктесін табу керек болсын. Бірінші шартты қанағаттандыратын нүктелердің геометриялық орны қайсыбір Ғ1 фигурасы болады, ал екінші шартты қанағаттандыратын нүктелердің геометриялық орны қайсыбір Ғ2 фигурасы болады. Ізделінді Х нүктесі Ғ1 фигурасына да, Ғ2 фигурасына да тиісті, яғни олардың қиылысу нүктесі болып табылады. Егер бұл гео-метриялық орындар қарапайым болса (мысалы, түзулер мен шеңберлерден құралса), біз оларды сала аламыз және қажетті Х нүктесін тауып алуға болады.

Осы әдіспен есептер шығарғанда мына жазықтықтағы нүктелердің негізгі геометриялық орындарын білу қажет:

Берілген екі нүктеден бірдей қашықтықта орналасқан нүктенің геометриялық орны

Берілген нүктеден берілген қашықтықта орналасқан нүктенің геометриялық орны

Берілген түзуден d қашықтықта орналасқан нүктенің геометриялық орны

Берілген параллель түзулерден бірдей қашықтықта орналасқан нүктенің геометриялық орны

Берілген бұрыштан бірдей қашықтықта орналасқан нүктенің геометриялық орны

Берілген кесінді берілген бұрышта көрінетін нүктенің геометриялық орны

Нүктелердің геометриялық орны әдісіне мысал

Үшбұрыштың бір қабырғасынан қалған екі қабырғасынан бірдей қашықтықта орналасқан нүктені табыңыз.

Талдау

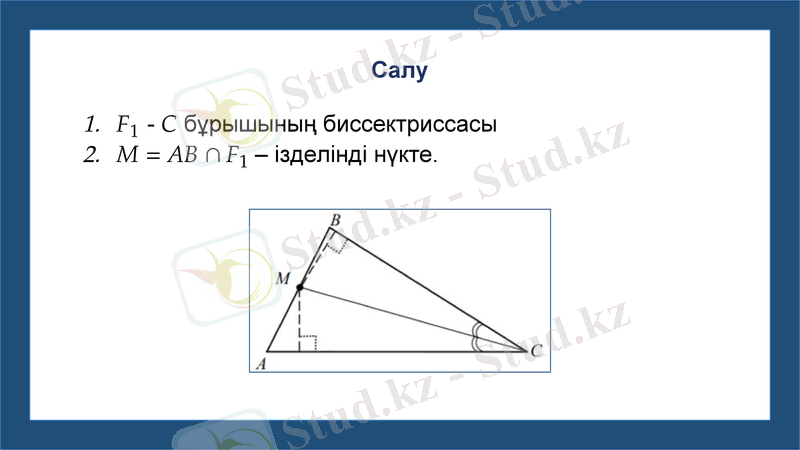
Салу

Дәлелдеу

Биссектриса анықтамасына сәйкес М нүктесінің есептің талаптарын байқау қиын емес.

Түрлендіру әдісі

Түрлендіруді геометриялық салулар теориясында қолдану геометриялық турлендірулер әдісі деп аталады. Түрлендірулер әдісінің негізгі мақсаты - берілген немесе ізделінді фигураларды түрлендіре отырып, есепті оңай шешілетіндей қарапайым түрге келтіру. Көптеген салу есептерін шешуде жазықтықты геометриялық түрлендіру нәтижелі қолданылады. Енді солардың түрлеріне тоқталып өтейік.

Параллель көшіру әдісі

Параллель көшіру вектор тапсырмасымен, яғни бағыты мен кесіндісімен толық анықталады.

Параллель көшірудің негізгі қасиеті: параллель көшіру кезінде сақталады

кесінді ұзындығы мен бұрыш өлшемі

кез-келген түзу оған параллель түзу сызықпен бейнеленеді

әр фигура оған тең фигурада көрсетіледі.

Есептер шығарған кезде кез-келген элементтерді (нүктелерді, кесінділерді) немесе қажетті пішінді біріктіру пайдалы болуы мүмкін. Бұған параллель көшіру арқылы оңай қол жеткізуге болады.

Осьтік симметрия әдісі

Осьтік симметрия әдісі көбінесе қажетті фигураның осьтік симметриясы бар мәселелерде қолданылады, ал симметрия осі осы сызықтардың бірі болып табылады. Осьтік симметрия сынық сызықтарды түзетумен байланысты мәселелерді шешуде, атап айтқанда, сынған сызықтардың қосындысы немесе айырмасы бар есептерді, сондай-ақ белгілі бір шаманың минималды немесе максималды мәндерін беретін фигураларды құру мәселелерін шешуде сәтті қолданылады.

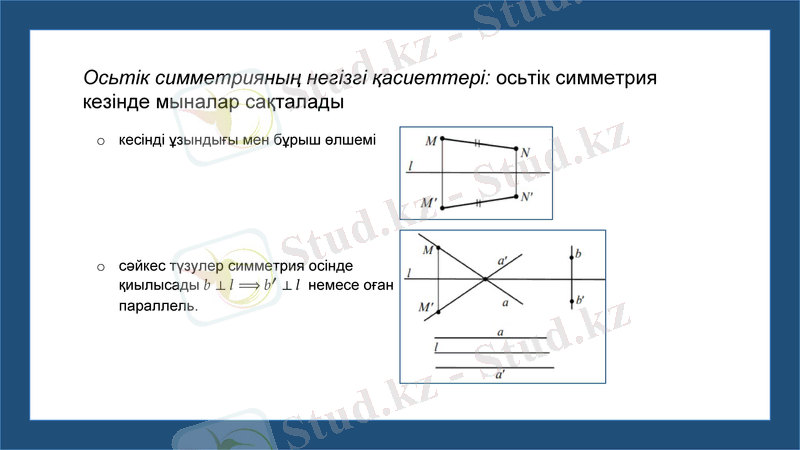
Осьтік симметрияның негізгі қасиеттері: осьтік симметрия кезінде мыналар сақталады

Центрлік симметрия әдісі

М және М' нүктелері О нүктесіне қатысты симметриялы деп аталады, егер О нүктесі МM’ кесіндісінің орта нүктесі болса.

Жазықтықтың нүктелерін түрлендіру, онда әрбір М нүктесі О нүктесіне қатысты оған симметриялы түрде M ' нүктесі көрсетілсе, О нүктесінде симметрия ортасы бар центрлік симметрия деп аталады.

Центрлік симметрия әдісінің негізгі қасиеттері: осьтік симметрия кезінде

түзу сызық оған параллель түзу сызықпен кескінделеді;

сәуле кері бағытталған сәуле болып кескінделеді;

симметрия нүктесі арқылы өтетін түзу, өзін бейнелейді;

кесінді тең кесіндіге кескінделеді;

бұрыш тең бұрыш болып бейнеленеді.

Гомотетия әдісі

Гомотетия әдісі бойынша, әдетте, бұрыштар, сегменттердің қатынасы және бір сызықтық элементы берілген салу есептері шешіледі. Сонымен қатар, егер қажетті F фигурасы бірнеше шарттарды қанағаттандырса, онда F1 фигурасын құруға болады, ол F гомотетикалық және бір сызықты өлшемнен басқа барлық шарттарды қанағаттандырады. F1 фигурасын салғаннан кейін F фигурасы салынады.

Гомотетия О центрін және k коэффициентін көрсету арқылы толығымен анықталады

Гомотетия әдісінің негізгі қасиеттері: гомотетия кезінде

Бұру әдісі

Бұру әдісі көбінесе айналмалы симметриясы бар фигураны салу қажет (теңбүйірлі үшбұрыш, шаршы, шеңбер және т. б. ) немесе берілген бұрышта фигураны салу қажет (және басқа қосымша шарттарды қанағаттандыратын) тапсырмаларды шешуде қолданылады.

бұру бұрышы

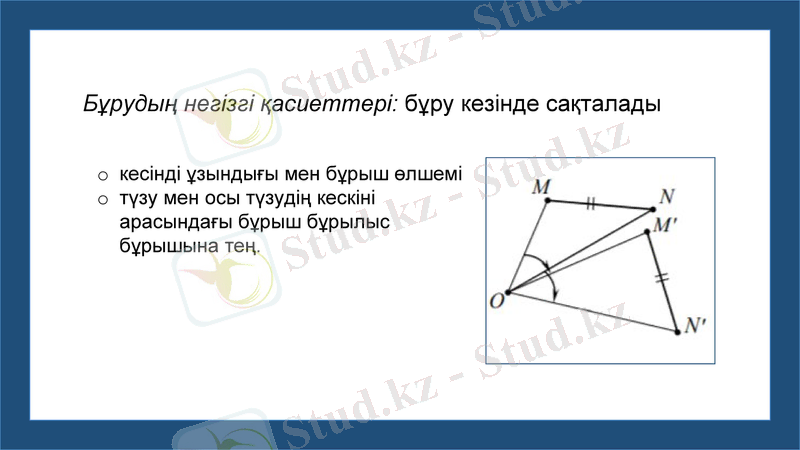
Бұрудың негізгі қасиеттері: бұру кезінде сақталады

кесінді ұзындығы мен бұрыш өлшемі

түзу мен осы түзудің кескіні арасындағы бұрыш бұрылыс бұрышына тең.

Алгебралық әдіс

Кейде талдау процесінде салу есептерін шешкен кезде қалаған фигураның құрылысы белгілі бір кесіндініңі сызуына дейін азайтылатындығын анықтауға болады, оның ұзындығы x осы кесіндінің ұзындығы арқылы белгілі бір формула бойынша көрсетілуі мүмкін. Бұл жағдайда біз есепті шешудің алгебралық әдісі туралы айтамыз.

Алгебралық әдіс бойынша берілген кесінділердің ұзындықтары а, в, с, . . . әріптерімен, ізделінді кесіндінің ұзындығы х әрпімен белгіленіп алынады да, есеп шартын пайдалана отырып ізделінді кесінділердің ұзындығын берілгендермен байланыстыратындай теңдеу құрылады. Құрылған теңдеуді шешіп, х-тің табылған өрнегінің геометриялық кескінін саламыз. Бұл - ізделінді кесінді болады.

Ұзындығы х кесіндісін, ұзындығы а, b, c кесінділері арқылы төмендегі формулалармен өрнектейді:

1. 3. Геометрия оқулықтарындағы «Салу есептері» тақырыбындағы оқу материалдарын талдау

Салу есептері жалпы білім беретін мектептің 7-сыныбына арналған оқулықтың «Шеңбер және салу есептері» тарауынан бастап өтіледі. Тараудың Геометриялық салу есептері тақырыбында салу есептері қарастырылады. Тақырыпта: қарапайым салу есептері, үш элементі бойынша үшбұрыш салу, салу есептерінің шешу кезеңдері түсіндіріледі.