Сызба геометриясы: нүктелер, түзулер және жазықтықтардың ортогональды проекциялары



Түзу сызбасы. Жазықтық.

СЫЗБА ГЕОМЕТРИЯСЫ -
бейнелерді құрастырумен айналысады және графикалық әдістерді қолдана отырып, олардың кескіндерінен кеңістік объектілерін зерттейді
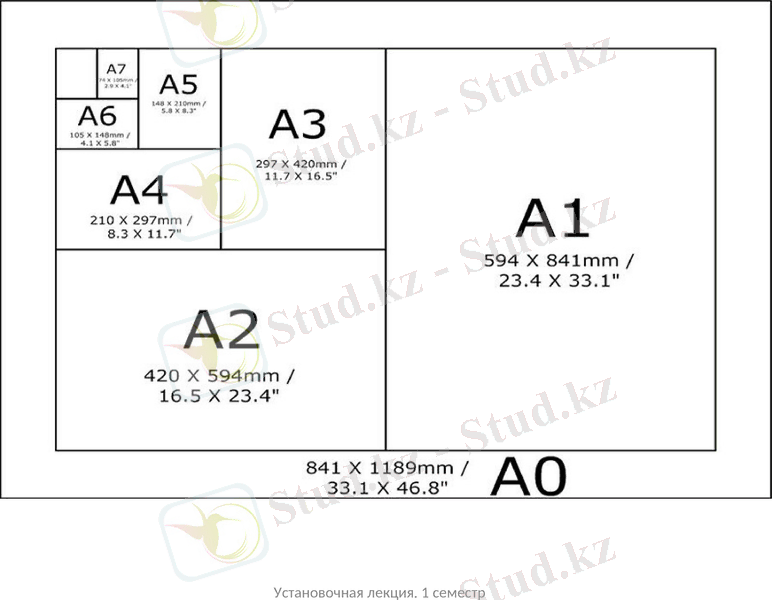
Установочная лекция. 1 семестр
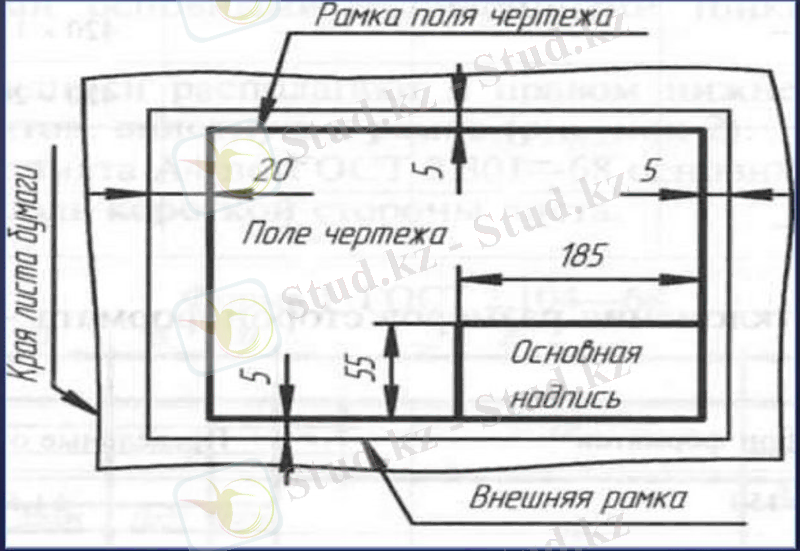
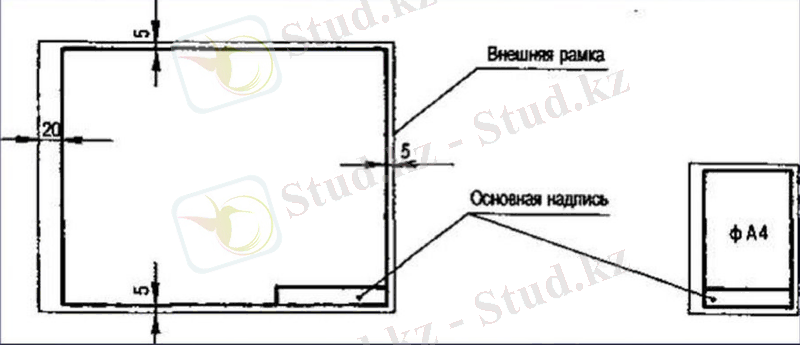
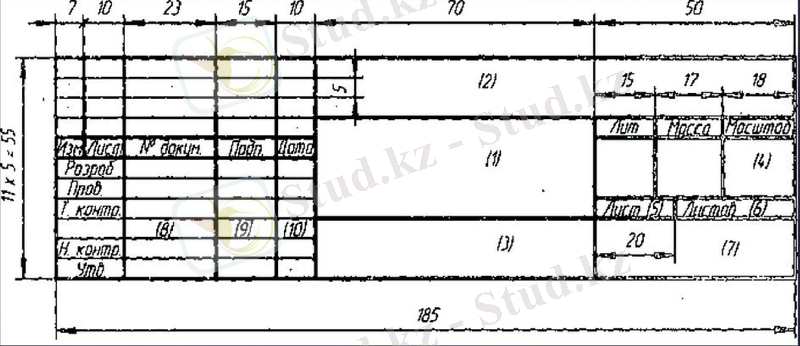


Установочная лекция. 1 семестр
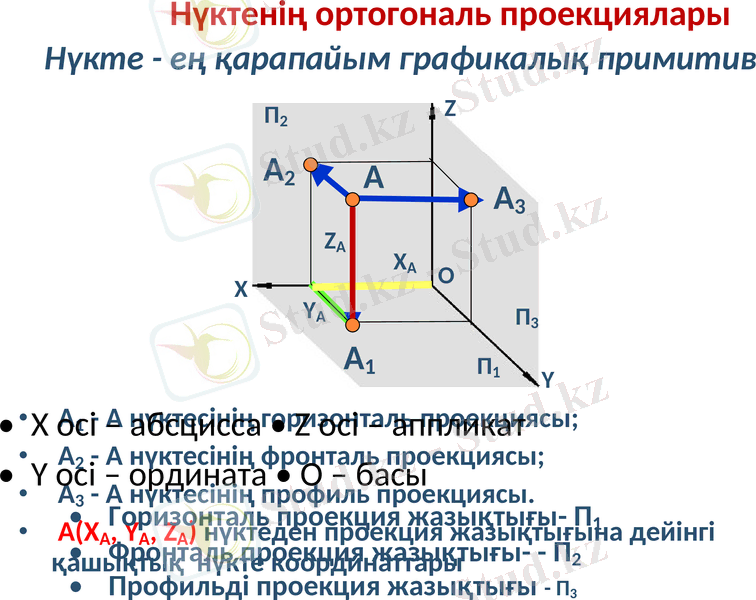
Нүктенің ортогональ проекциялары
А1 - А нүктесінің горизонталь проекциясы;
А2 - А нүктесінің фронталь проекциясы;
А3 - А нүктесінің профиль проекциясы.
А(XА, YА, ZА) нүктеден проекция жазықтығына дейінгі қашықтық нүкте координаттары
X
Y
O
П1
П3
П2
XA
Z
А
А1
А2
А3
YA
ZA
Нүкте - ең қарапайым графикалық примитив
Горизонталь проекция жазықтығы- П1
Фронталь проекция жазықтығы- П2
Профильді проекция жазықтығы - П3
X осі - абсцисса • Z осі - аппликат
Y осі - ордината • O - басы
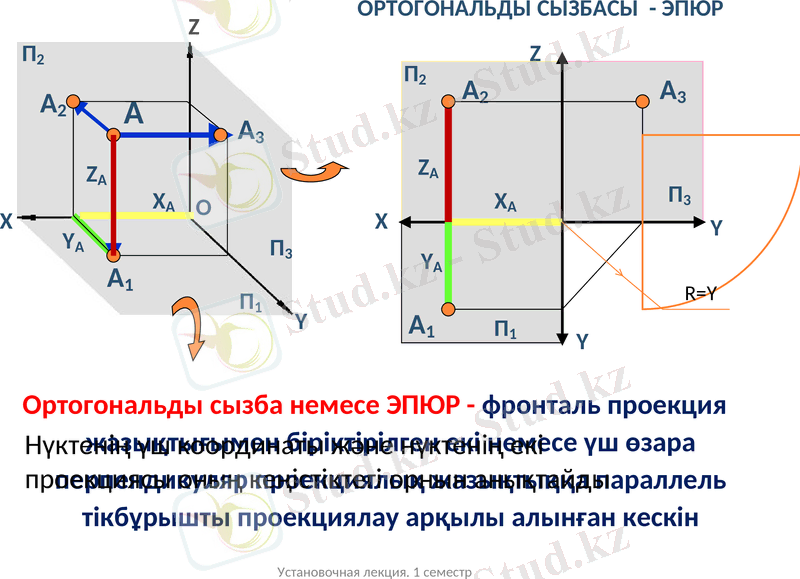
ОРТОГОНАЛЬДЫ СЫЗБАСЫ - ЭПЮР
Ортогональды сызба немесе ЭПЮР - фронталь проекция жазықтығымен біріктірілген екі немесе үш өзара перпендикуляр проекциялық жазықтыққа параллель тікбұрышты проекциялау арқылы алынған кескін
Z
Y
Y
X
П3
П1
П2
XA
А2
А3
YA
ZA
X
Y
O
П1
П3
П2
XA
Z
А
А1
А2
А3
YA
ZA
А1
Нүктенің үш координаты және нүктенің екі проекциясы оның кеңістіктегі орнын анықтайды
Установочная лекция. 1 семестр
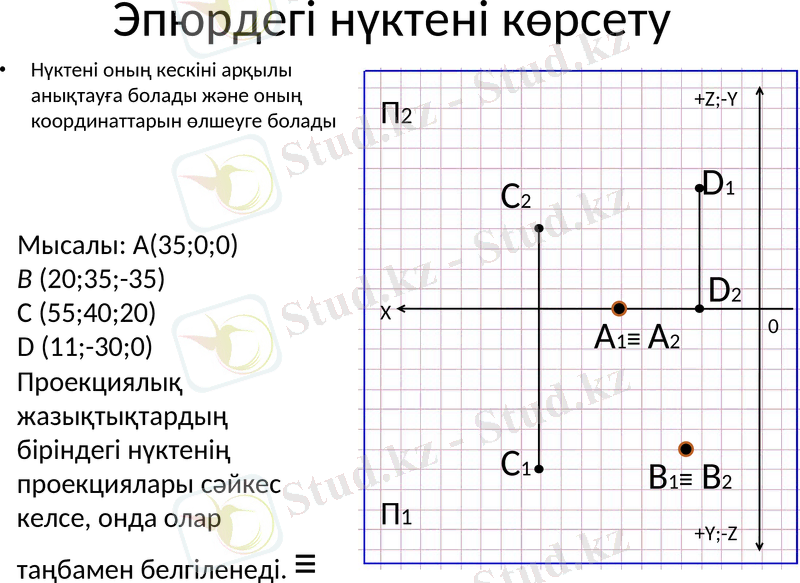
Эпюрдегі нүктені көрсету
Нүктені оның кескіні арқылы анықтауға болады және оның координаттарын өлшеуге болады
X
+Z; -Y
+Y; -Z
0
С1
С2
B2
B1≡
П1
П2
Проекциялық жазықтықтардың біріндегі нүктенің проекциялары сәйкес келсе, онда олар таңбамен белгіленеді. ≡
Мысалы: A(35; 0; 0)
В (20; 35; -35)
С (55; 40; 20)
D (11; -30; 0)
A2
A1≡
D1
D2
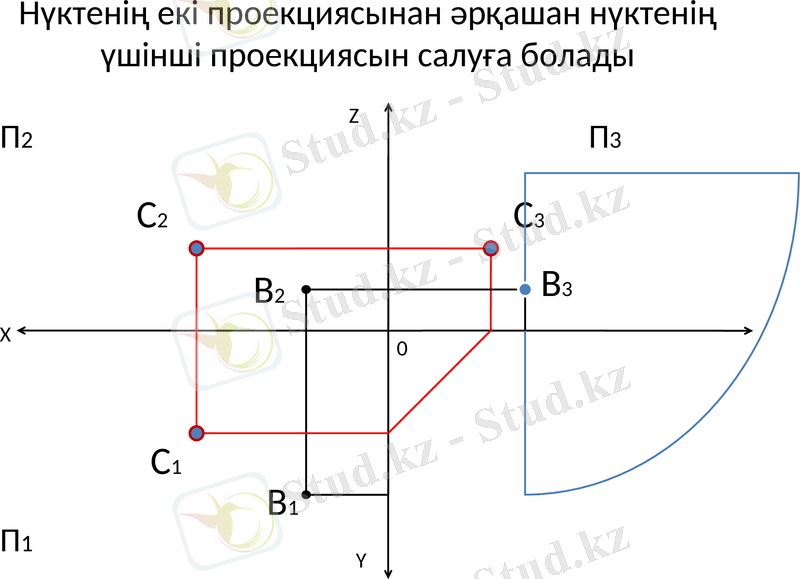
Нүктенің екі проекциясынан әрқашан нүктенің үшінші проекциясын салуға болады
X
Z
Y
0
B2
B1
П1
П2
С2
С1
С3
П3
В3
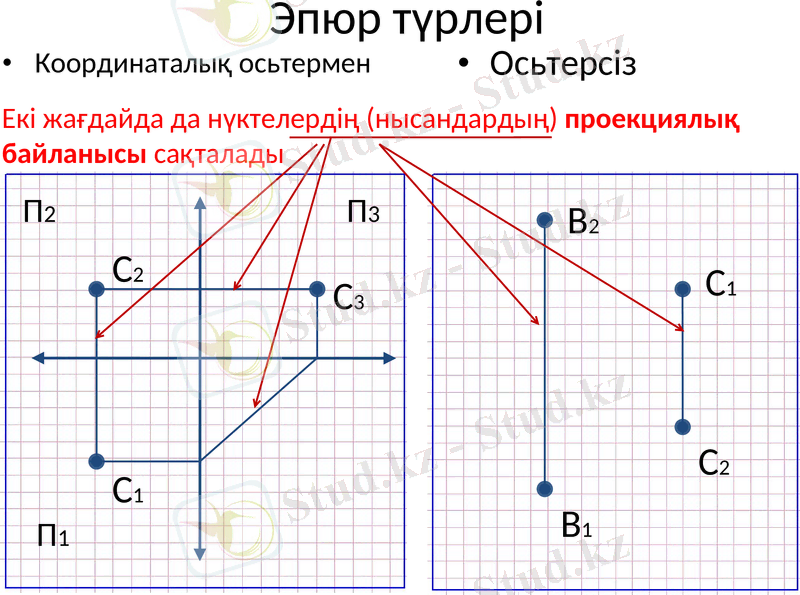
Эпюр түрлері
Координаталық осьтермен
Осьтерсіз
B2
B1
П1
П2
С2
С1
С3
П3
С1
С2
Екі жағдайда да нүктелердің (нысандардың) проекциялық байланысы сақталады

Түзу сызық - екі нүкте арасындағы ең қысқа қашықтық

Кеңістіктегі сызықтар жалпы және жеке позицияларды алуы мүмкін
Жалпы түзулер проекция жазықтықтарының ешқайсысына параллель де, перпендикуляр да емес
Жартылай түзулер проекция жазықтықтарына параллель немесе перпендикуляр болады
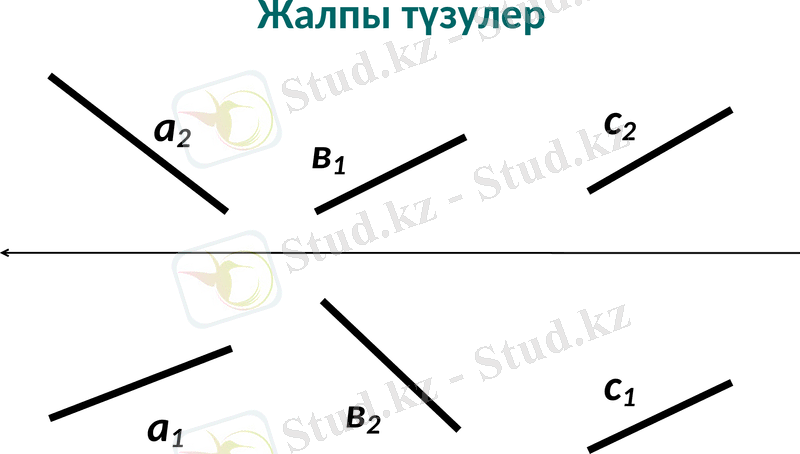
Жалпы түзулер
а2
в1
с2
а1
в2
с1

Жеке позицияның тікелей сызықтары
• проекциялық жазықтықтарға перпендикуляр түзулер - проекциялаушы түзулер
• проекция жазықтықтарына параллель түзулер - деңгей түзулері

Проекциялар жазықтықтарына перпендикуляр белгілі бір позиция түзулері 1. Проекциялық түзулер
Көлденең проекция сызығы
А
B1
А1
B2
А2
B
Ξ
Z
X
Y
Z
X
Y
А1 Ξ B1
B2
А2
О
О
AB ┴ П1
IА2В2I = I АВ I
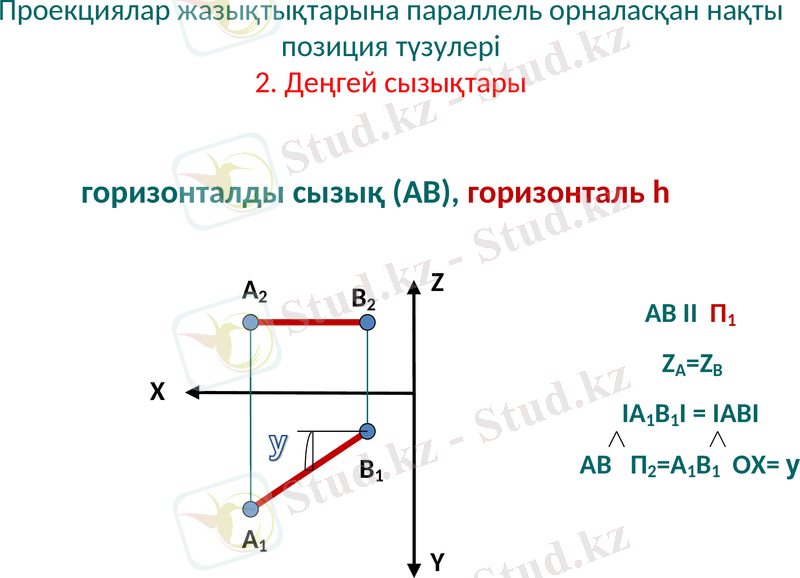
Проекциялар жазықтықтарына параллель орналасқан нақты позиция түзулері 2. Деңгей сызықтары
горизонталды сызық (АВ), горизонталь h
X
Z
Y
А2
А1
В2
В1
AВ II П1
ZА=ZB
IА1В1I = IАВI
АВ П2=А1В1 OX= y
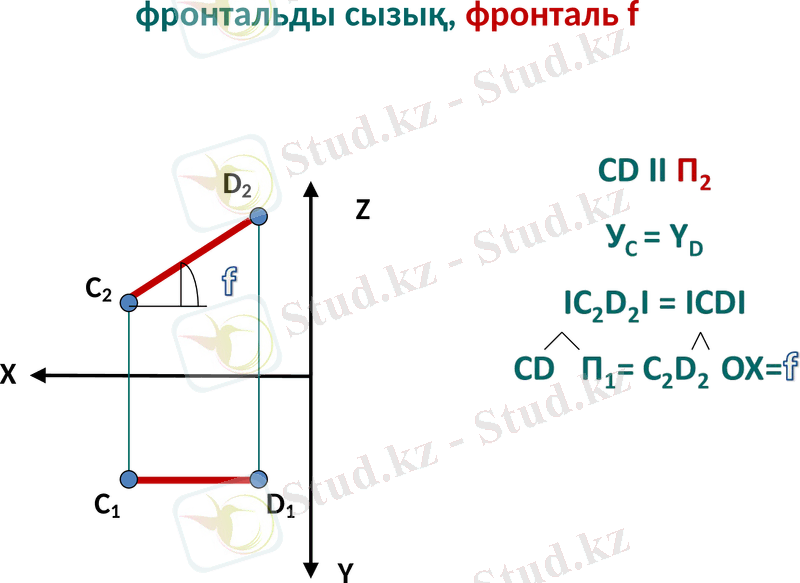
фронтальды сызық, фронталь f
X
Z
Y
C2
C1
D2
D1

Жазықтық
Эпюр бойынша жазықтықты көрсету
Жазықтықтың арнайы сызықтары
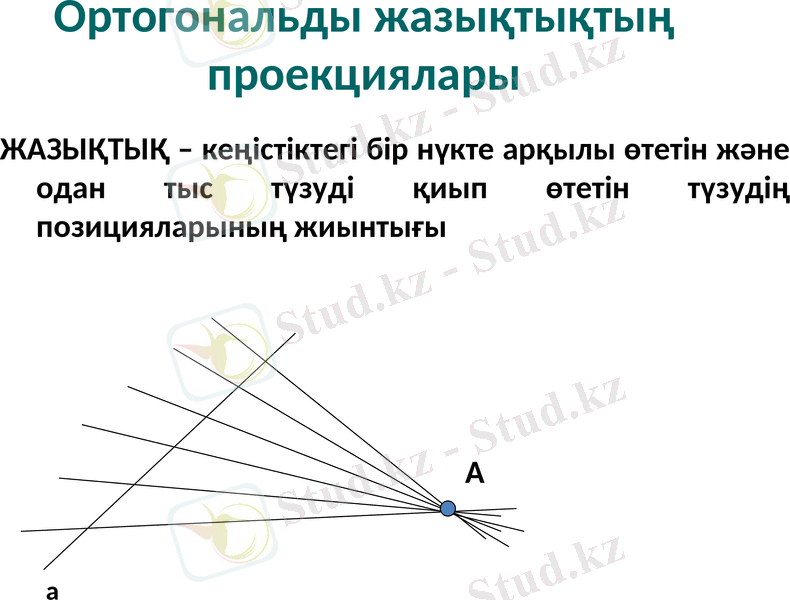
Ортогональды жазықтықтың проекциялары
ЖАЗЫҚТЫҚ - кеңістіктегі бір нүкте арқылы өтетін және одан тыс түзуді қиып өтетін түзудің позицияларының жиынтығы
A
a
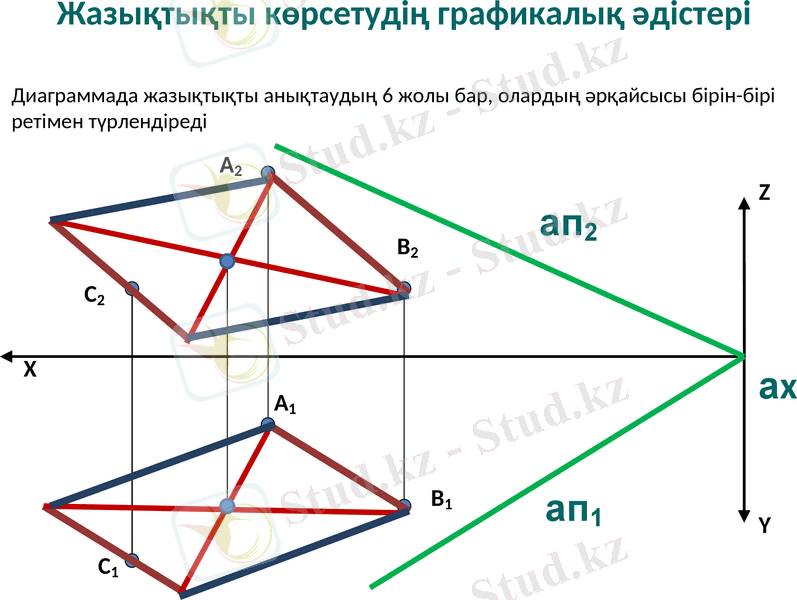
Жазықтықты көрсетудің графикалық әдістері
X
Z
Y
А2
А1
В1
C2
C1
В2
Диаграммада жазықтықты анықтаудың 6 жолы бар, олардың әрқайсысы бірін-бірі ретімен түрлендіреді
ax
aп2
aп1
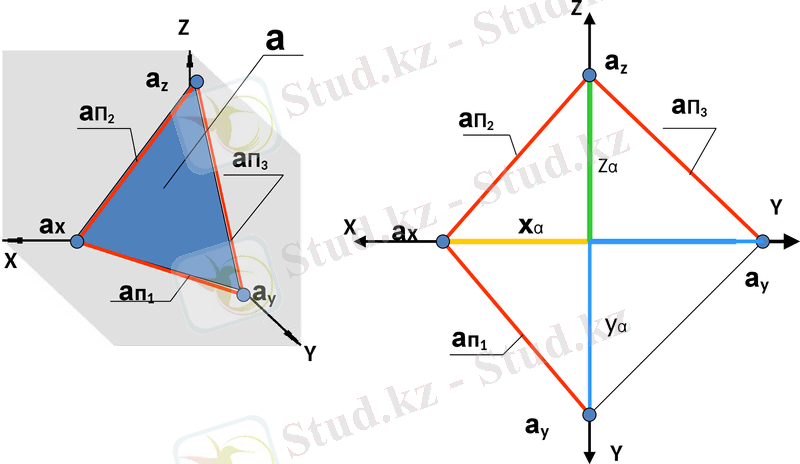
Z
X
Y
Y
aП2
aп1
aП3
ax
ay
az
Z
X
aп1
aП3
aП2
ax
ay
az
a
ay
Y
xα
yα
Zα

Жазықтықтың орналасуы
Проекциялық жазықтықтарға қатысты кеңістіктегі жазықтықтар:
• жеке позиция
• жалпы жағдай
2. Жеке позициядағы жазықтықтар бөлінеді
проекция жазықтықтарына параллель жазықтықтар - деңгей жазықтықтары
проекциялық жазықтықтарға перпендикуляр жазықтықтар - проекциялаушы жазықтықтар
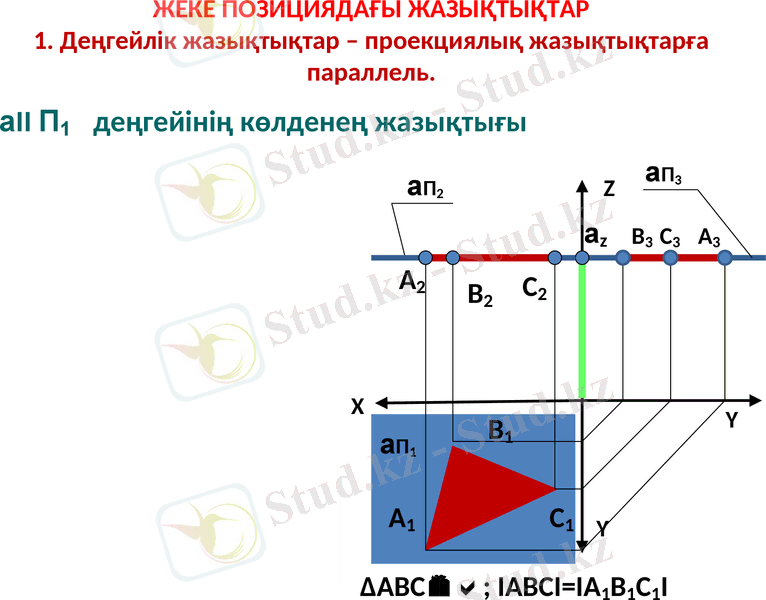
ЖЕКЕ ПОЗИЦИЯДАҒЫ ЖАЗЫҚТЫҚТАР 1. Деңгейлік жазықтықтар - проекциялық жазықтықтарға параллель.
aII П1 деңгейінің көлденең жазықтығы
Z
X
Y
Y
aП2
aП3
az
Y
Z
X
aП3
aП2
az
a
А1
В1
С1
А2
В2
С2
А1
С1
В1
А2
В2
С2
ΔАВС; IABCI=IA1B1C1I
В3 С3 А3
aП1
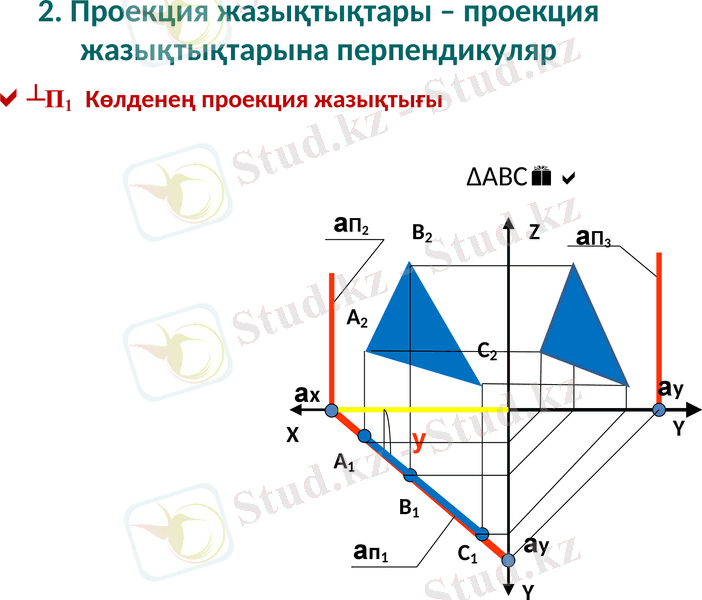
2. Проекция жазықтықтары - проекция жазықтықтарына перпендикуляр
┴П1 Көлденең проекция жазықтығы
X
Y
Y
aП2
aП3
Z
X
aп1
aП2
ax
ax
Z
aп1
aП3
a
Y
ay
y
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz