Функцияның қасиеттерін үйрену

Презентация қосу

Сабақтың тақырыбы:
Сабақтың мақсаттары:

Функцияның қасиеттерін үйрену.
Есептерді шығару барысында
функцияның қасиеттерін тани білу.
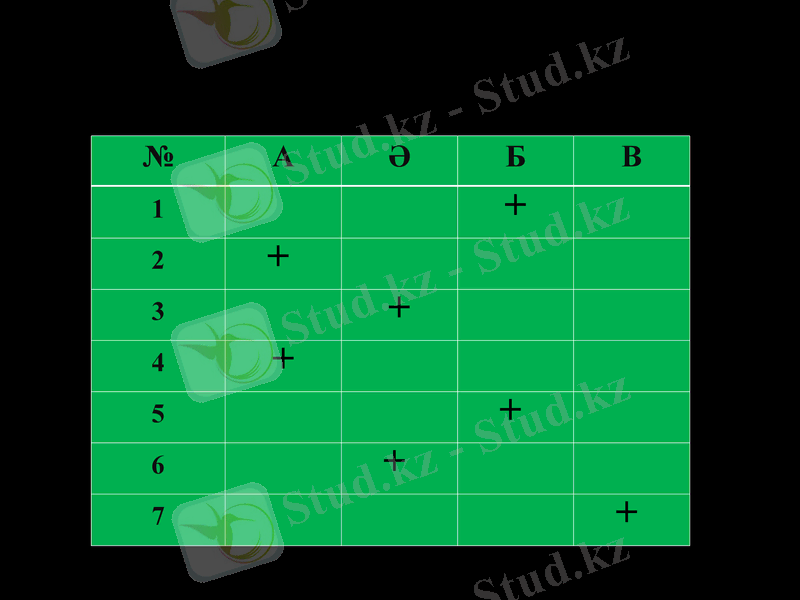
Жауапты тексеріңіз!
№ А Ә Б В
1 +
2 +
3 +
4 +
5 +
6 +
7 +
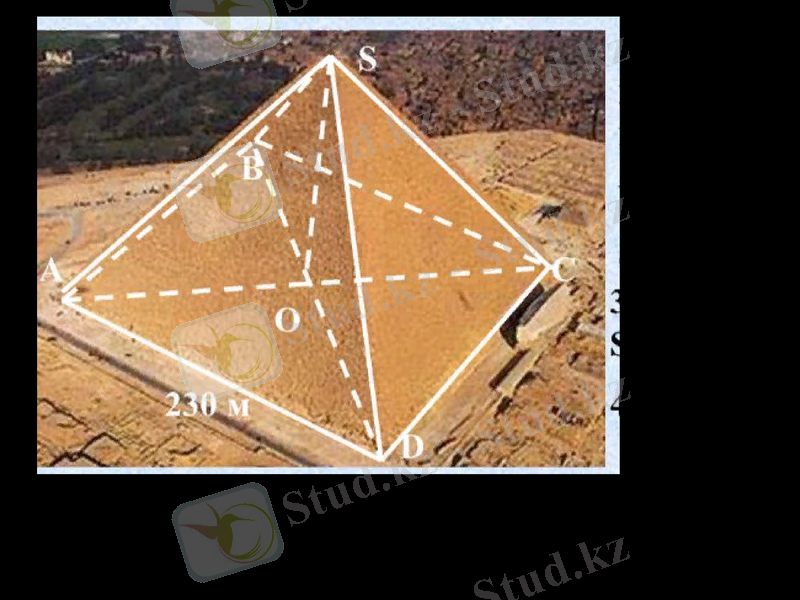
• Оқулықтан 2.12 суретты немесе
интернеттен нур султандағы
бейбітшілік пен келісім сарайы
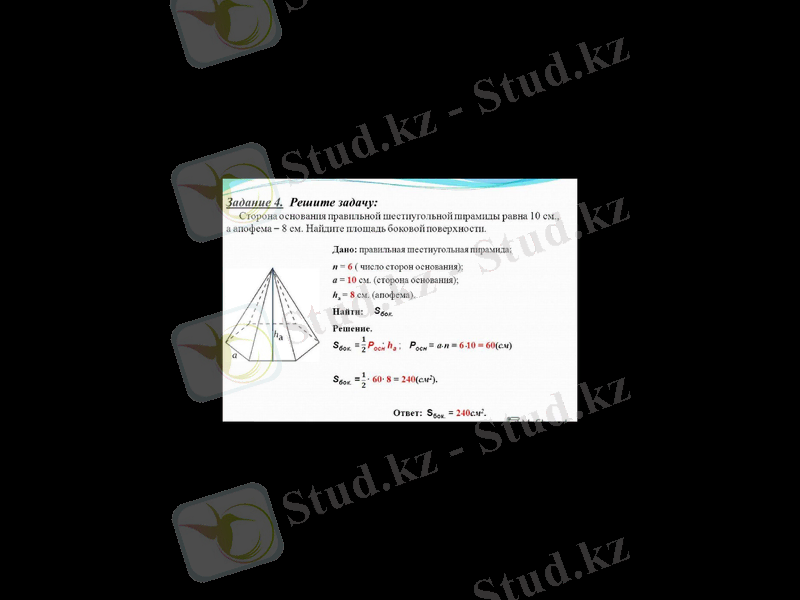
В деңгейі есептері
Пирамиданың табаны
қабырғалары 6 см және 8 см
болатын тіктөртбұрыш;
пирамиданың әр қабырғасы 13 см-
ге тең. Пирамиданың биіктігін
тап.
Бaғaлaу кpитеpийі: Білім aлушы
•Берілген тапсырмаға қандай фоpмулaлap пайдаланатынын
aнықтaйды;
•Фоpмулaлaрды есептеp шығapудa тиімді қолдaнaды;
•Сызбаларын сызады.
Дескpиптоp:
•Есепке қажетті фоpмулaлapын біледі;
•Бүйір қырларын aнықтaйды,
•Пирамида биіктігін табады;
•Дұрыс пирамиданың бүйір бетінің және толық бетінің
ауданын табады;
•Сызбаларын салады.
Анықтама
• Анықталу облысының кез келген
нүктесіндегі f(х) функцияның мәндерінің
абсолют шамасы белгілі бір b>0 санынан
кіші
немесе оған тең болса, яғни |f(x)|≤b, x
X, онда ол осы жиында шектелген
функция деп аталады.
• Мысалы: y=sinx, y=cosx функцияларының
мәндерінің абсолют шамалары 1 санынан
аспайды.
Анықтама

• Анықталу облысының қайсыбір
аралықтарында функция тек оң мәндерді
(оның графигі Ох осінің жоғарғы жағында
орналасқан), ал басқа аралықтарында тек
теріс мәндерді (график Ох осінің төменгі
жағында орналасқан) қабылдаса, онда
мұндай аралықтарды функция
таңбасының тұрақтылық аралықтары
деп атайды.
Анықтама
• Егер у = f(х) функциясының анықталу
облысындағы
x1 x 2 f (x ) f (x )
1 2
кез келген сандары үшін f ( x1 ) f ( x 2 )
теңсіздігі орындалса, онда функция өспелі, ал
теңсіздігі орындалса, онда ол кемімелі
деп аталады
• xЕгер
1 x 2 у = f(х) функциясының анықталу
f ( x1 ) f ( x 2 )
облысындағы f ( x1 ) f ( x 2 )
кез келген сандары үшін
теңсіздігі орындалса, онда функция кемімейтін,
ал теңсіздігі орындалса, онда ол өспейтін
функция деп аталады. Өспелі, кемімелі,
кемімейтін, өспейтін функцияларды
бірсарынды(монотонды) функциялар деп атайды.
• а нүктесінің аймағы деп осы нүктені қамтитын
кез келген аралықта айтады.
Анықтама
• Егер x0 нүктесінің қандай да бір аймағынан
алынған барлықf ( x) хf үшін
( x0 ) теңсіздігі x 0
орындалса, онда нүктесі f(х) f ( x) f ( x0 )
функциясының минимум, ал
теңсіздігі орындалса, максимум нүктесі
деп аталады. Минимум және максимум
нүктелерін экстремум нүктелері деп атайды.

1-сурет
Анықтама
• Егер у = f(х) функциясы Х анықталу
облысында бірсарынды өспелі(кемімелі)
функция болса, онда осы функцияның У
мәндер жиынында анықталған бірсарынды
өспелі(бірсарынды кемімелі) функция оның
кері функциясы болады.
• Егер f функциясының анықталу облысы g
функциясының мәндерінің облысы болса, f
функциясының мәндерінің облысы g
функциясының анықталу облысы болса, онда g
функциясы f функциясына кері функция деп
аталады
• D(f)=E(g) және D(g)=E(f)
• Мысалы: у=3x+5 функциясына кері
функция анықтаңыз.
Ол үшін х айнымалысын у аынымалысы
арқылы өрнектейміз.
y 5
3x=y-5;x
; енді х пен у
айнымалыларының орнын ауыстырамыз
х 5
Сонда у
шығады. Осы функция
у=3x+5 функциясына кері функция.
х 5
Сонда у=3x+5 тура функция,3
у

кері функция.

2-сурет

Ұқсас жұмыстар

Анықталған интеграл және оның қолданылулары

Интегралдық есептеу термині мен интеграл таңбасы Лейбництен бастап қолданылып

Ондық логарифм

Квадрат теңсіздік

Бүгінгі сабақта менің білгенім

Дифференциалданатын барлық нақты функцияларды табыңдар, егер

Периодты функциялар

Аргумент өсімшесі

Анықталмаған интеграл қасиеттері

Көрсеткіштік функцияның графигі мен қасиеттері

Пәндер