Геометрия: төртбұрыштар мен көпбұрыштар, аудан мен ұқсастықтар; негізгі теоремалар және тригонометриялық қатынастар



Геометрия.
Райымбекова А. А
НИШ ФМН Астана

Мазмұны
Төртбұрыштар
Көпбұрыштар
Параллелограмм
Трапеция
Фалес теоремасы
Тіктөртбұрыш
Ромб
Остік және централік симметрия
Аудан
Ауданның қасиеттері
Тіктөртбұрыштың ауданы
Параллелограмның ауданы
Үшбұрыштың ауданы
Трапецияның ауданы
Пифагор теоремасы
Ұқсас үшбұрыштар
Ұқсас үшбұрыштар анықтамасы
Үшбұрыштардың ұқсастық белгілері
Үшбұрыштың орта сызығы
Тікбұрышты үшбұрыштың қабырғалары және бұрыштарының арасындағы қатынас
А
В
С
D
E
F

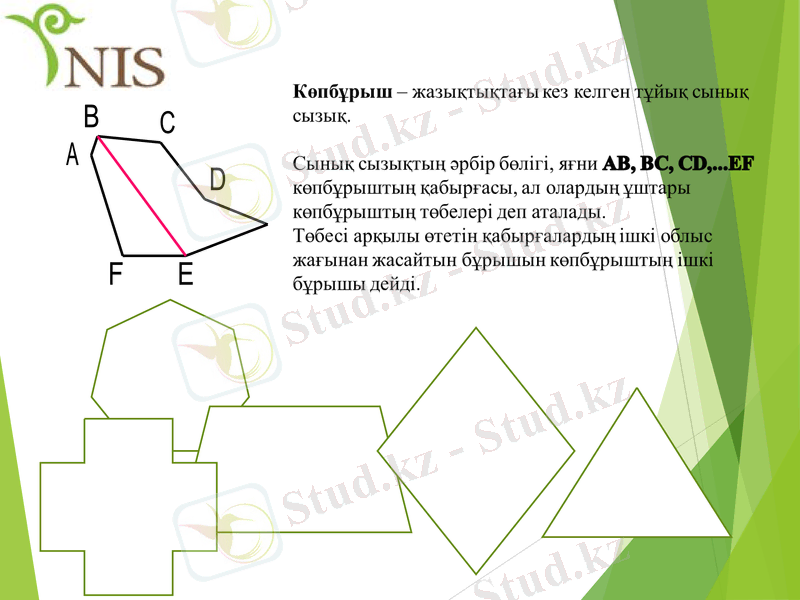
Көпбұрыш ішкі бөлігі
Көпбұрыштын сыртқы бөлігі
(көпбұрыш жазықтығынан тыс жазықтық бөлігі)
(көпбұрыш жазықтығы)
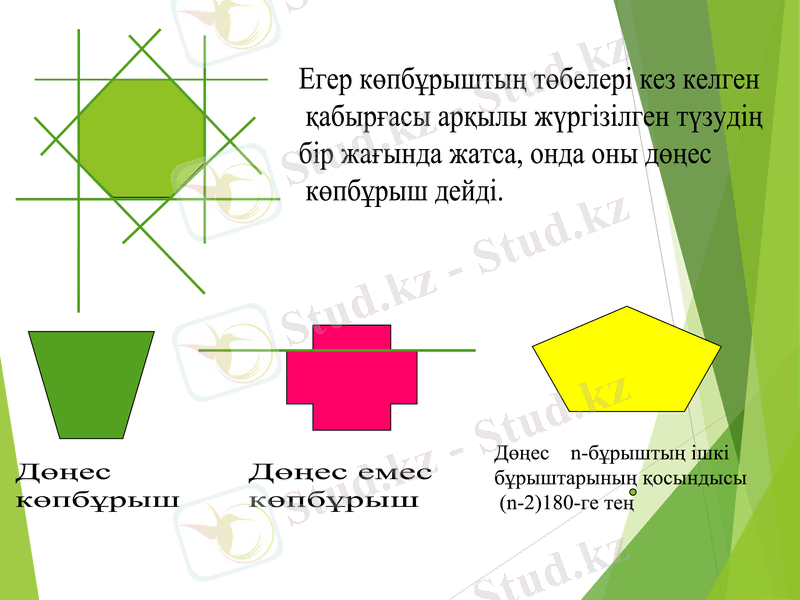
Егер көпбұрыштың төбелері кез келген
қабырғасы арқылы жүргізілген түзудің
бір жағында жатса, онда оны дөңес
көпбұрыш дейді.
Дөңес
көпбұрыш
Дөңес емес
көпбұрыш
Дөңес n-бұрыштың ішкі
бұрыштарының қосындысы
(n-2) 180-ге тең

Төртбұрыш
Іргелес емес екі бұрышы
қарама-қарсы бұрыштар деп аталады
А
B
C
D
Дөңес төртбұрыштың
бұрыштарының қосындысы 360-қа тең
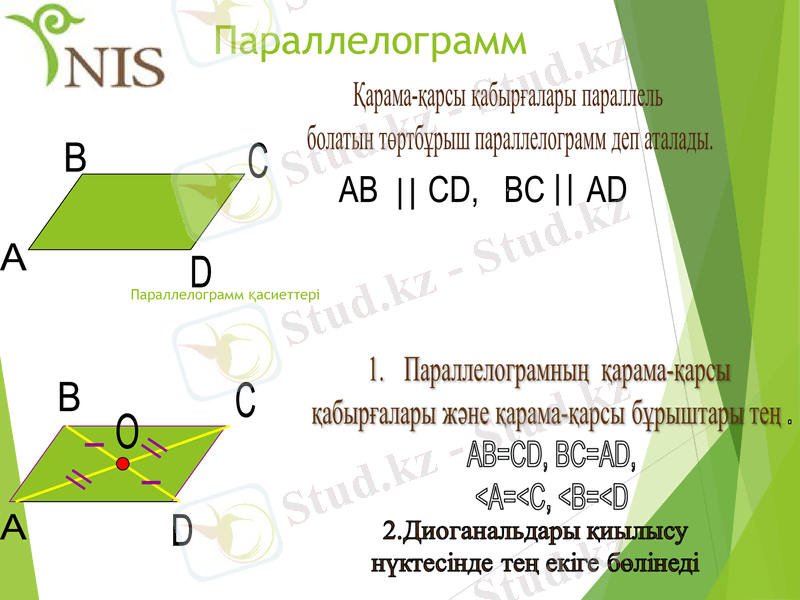
Параллелограмм
А
В
С
D
AB CD, BC AD
Параллелограмм қасиеттері

Параллелограмның белгілері
Егер төртбұрыштың екі қабырғасы тең және параллель болса, онда ол-параллелограмм
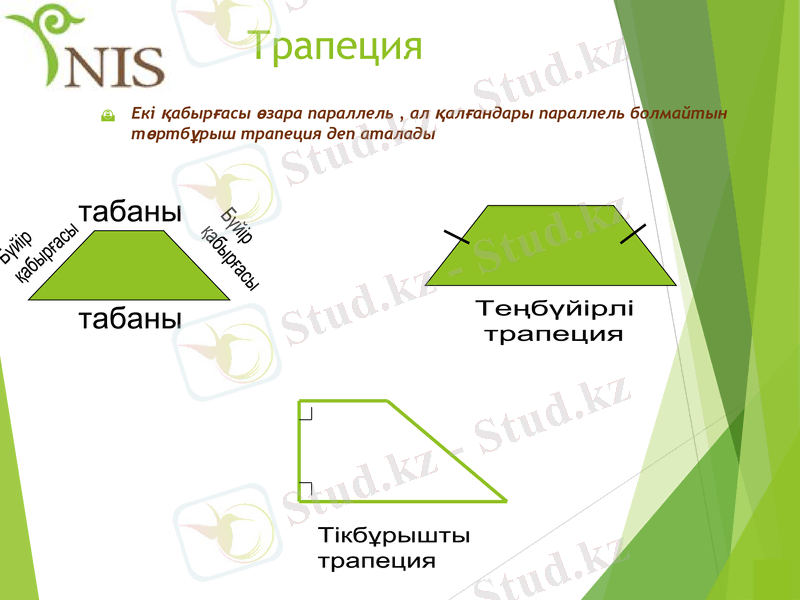
Трапеция
Екі қабырғасы өзара параллель, ал қалғандары параллель болмайтын төртбұрыш трапеция деп аталады
табаны
табаны
Бүйір
қабырғасы
Бүйір
қабырғасы
Теңбүйірлі
трапеция
Тікбұрышты
трапеция
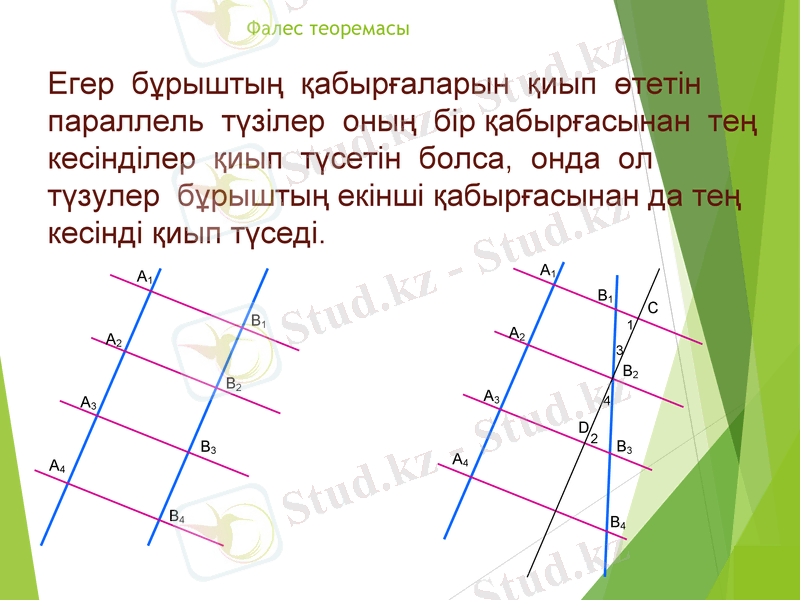
Егер бұрыштың қабырғаларын қиып өтетін параллель түзілер оның бір қабырғасынан тең кесінділер қиып түсетін болса, онда ол түзулер бұрыштың екінші қабырғасынан да тең кесінді қиып түседі.
Фалес теоремасы
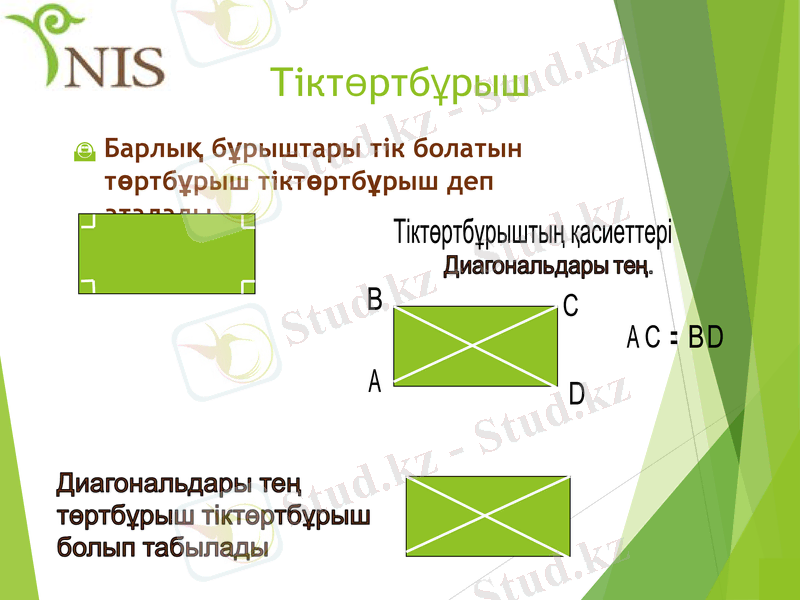
Тіктөртбұрыш
Барлық бұрыштары тік болатын төртбұрыш тіктөртбұрыш деп аталады.
Тіктөртбұрыштың қасиеттері
А
В
С
D
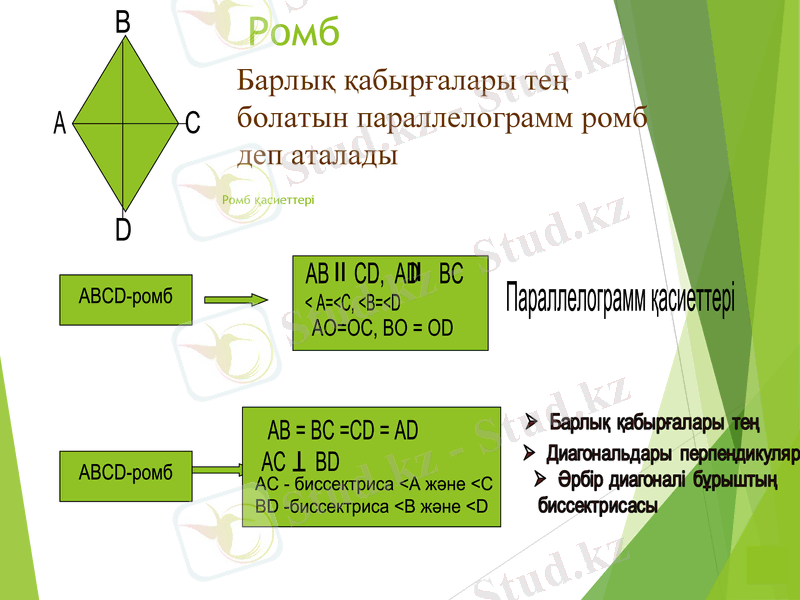
Ромб
АВ СD, АD ВС
< A=
AO=OC, BO = OD
Параллелограмм қасиеттері
А
В
D
С
Барлық қабырғалары тең
болатын параллелограмм ромб
деп аталады
Ромб қасиеттері
а
Екі және нүктелері а түзуіне қарағанда симметриялы деп аталады, егер а түзуі кесіндісінің ортасынан өтіп оған перпендикуляр болса
а симметрия осі деп аталады.
Фигура а түзуіне қарағанда симметриялы деп аталады, егер фигураның а түзуіне қарағанда симметриялы әрбір нүктесі осы фигураға тиісті болса
а түзуі фигураның симетрия осі деп аталады
а
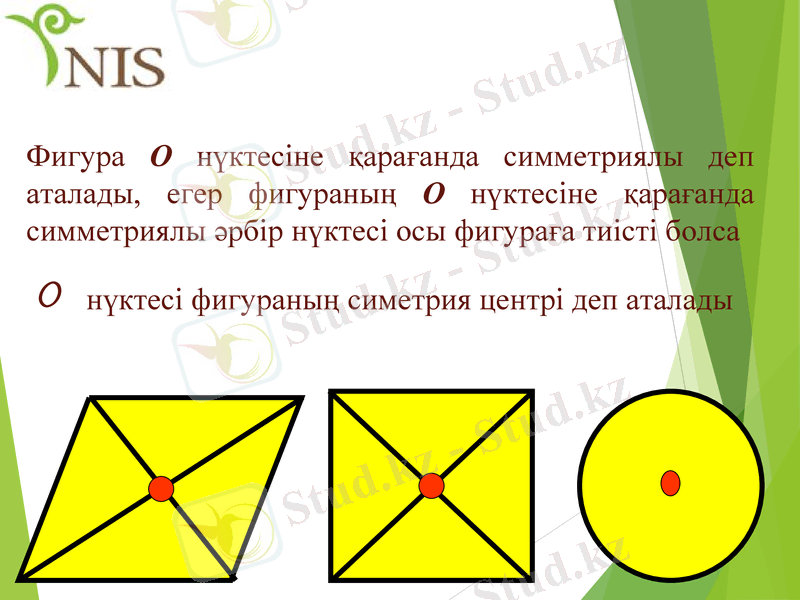
Фигура О нүктесіне қарағанда симметриялы деп аталады, егер фигураның О нүктесіне қарағанда симметриялы әрбір нүктесі осы фигураға тиісті болса
О нүктесі фигураның симетрия центрі деп аталады
Аудан ұғымы. Ауданның қасиеттері.
Жазық пішіндерді қамтитын бірлік квадраттардың (қабырғалары ұзындықтың бірлігіне тең) санымен анықталады
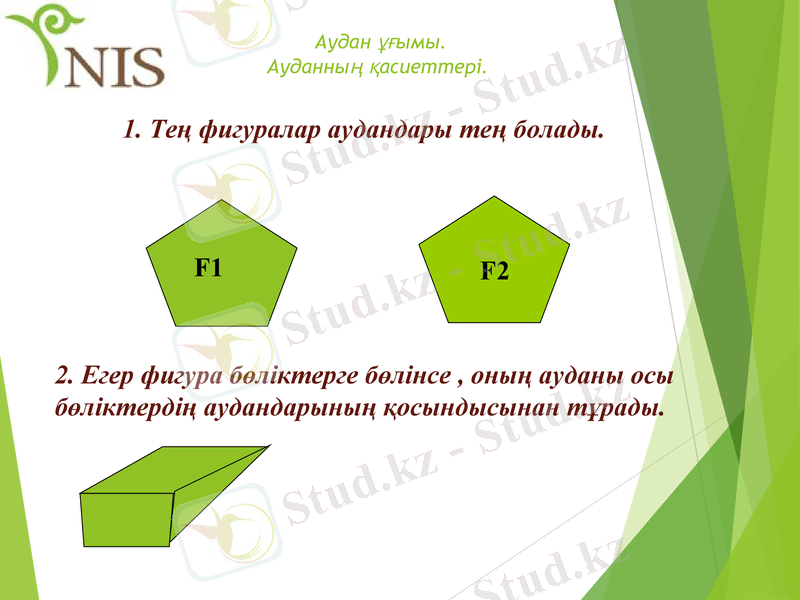
1. Тең фигуралар аудандары тең болады.
2. Егер фигура бөліктерге бөлінсе, оның ауданы осы бөліктердің аудандарының қосындысынан тұрады.
Аудан ұғымы.
Ауданның қасиеттері.
Теорема.
Тіктөртбұрыштың ауданы оның іргелес қабырғаларының көбейтіндісіне тең
А
В
С
D
S =ab
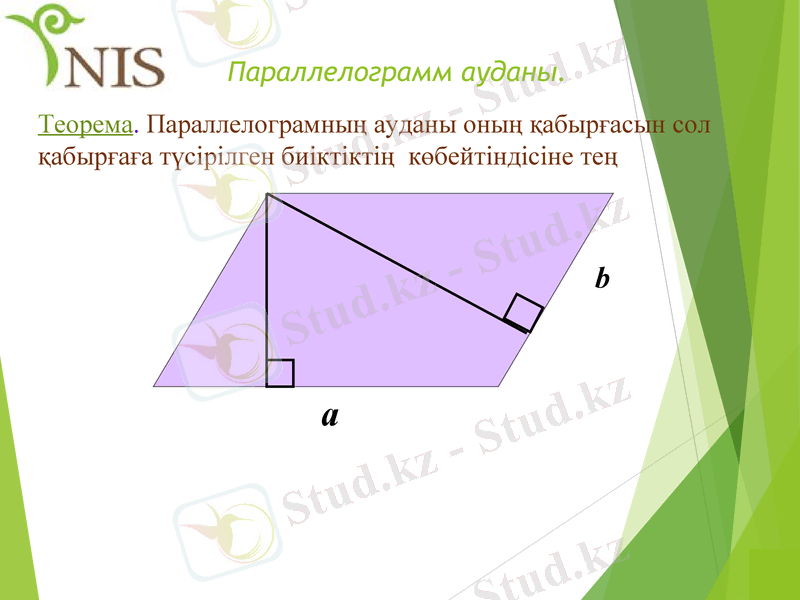
Параллелограмм ауданы.
Теорема. Параллелограмның ауданы оның қабырғасын сол қабырғаға түсірілген биіктіктің көбейтіндісіне тең
a
b
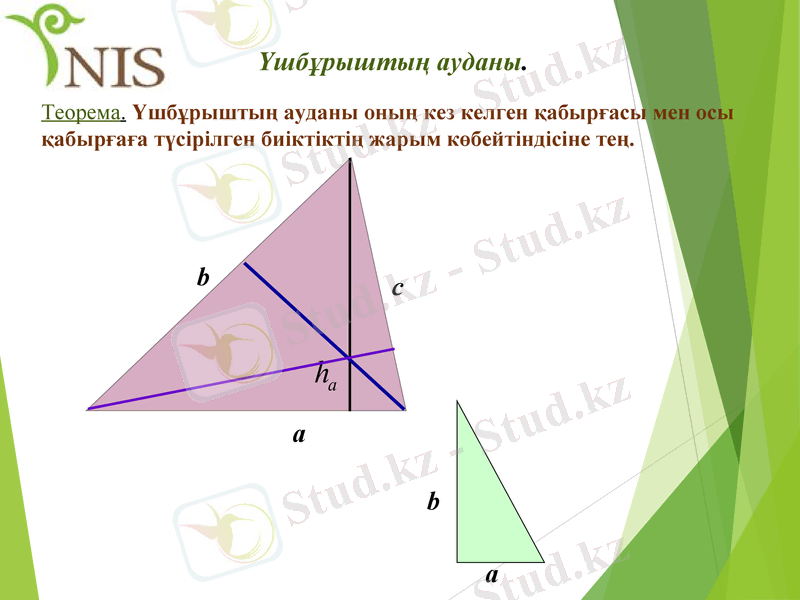
Үшбұрыштың ауданы.
Теорема. Үшбұрыштың ауданы оның кез келген қабырғасы мен осы қабырғаға түсірілген биіктіктің жарым көбейтіндісіне тең.
a
b
c
b
a
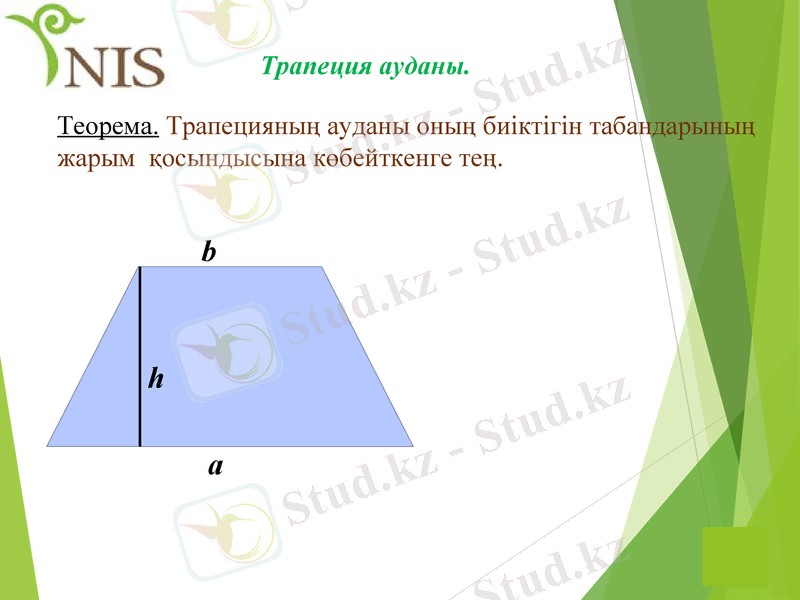
Трапеция ауданы.
Теорема. Трапецияның ауданы оның биіктігін табандарының жарым қосындысына көбейткенге тең.
Тікбұрышты үшбұрыштың гипотенузасының квадраты оның катеттерінің квадраттарының қосындысына тең
c²=a²+b²
с - гипотенуза
a, b - катеттер.
Пифагор теоремасы
Үшбұрыштар ұқсастығы
С
А
В
A1
C1
B1
AB и A1B1, BC и B1C1, AC и A1C1 - сходственные стороны
Екі үшбұрыш ұқсас болып табылады, егер олардың сәйкес бұрыштары тең және қабырғалары пропорционал болса.
Теорема!
I ұқсастық белгісі
Егер бір үшбұрыштың екі бұрышы екінші үшбұрыштың екі бұрышына тең болса, онда бұл үшбұрыштар ұқсас
II ұқсастық белгісі
Егер бір үшбұрыштың екі қабырғасы екінші үшбұрыштың екі қабырғасына пропорционал және олардың арасындағы бұрыштар тең болса, онда бұл үшбұрыштар ұқсас.
Теорема!
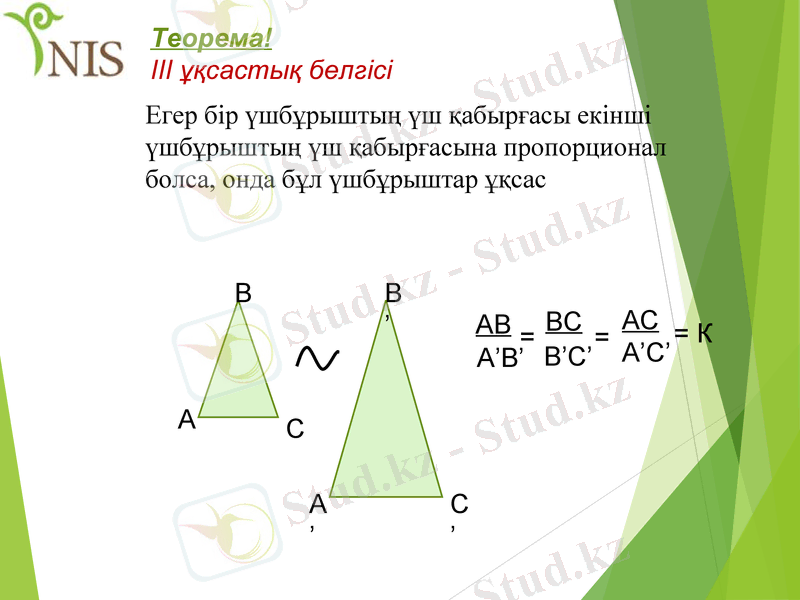
III ұқсастық белгісі
Егер бір үшбұрыштың үш қабырғасы екінші үшбұрыштың үш қабырғасына пропорционал болса, онда бұл үшбұрыштар ұқсас
АВ
A’B’
=
BС
B’C’
AC
A’C’
=
= К
В
А
С
A’
B’
C’
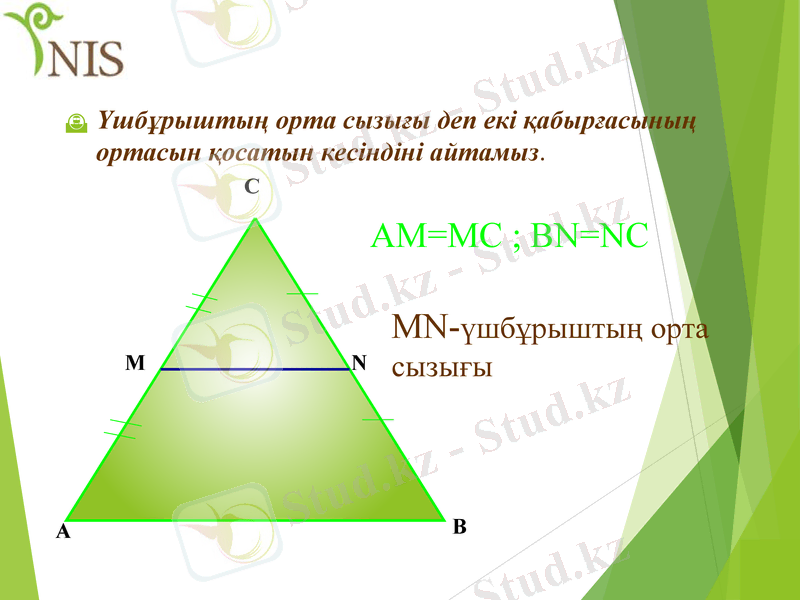
Үшбұрыштың орта сызығы деп екі қабырғасының ортасын қосатын кесіндіні айтамыз.
А
В
С
М
N
AM=MC ; BN=NC
MN-үшбұрыштың орта сызығы
Үшбұрыштың орта сызығы оның бір қабырғасына параллель және ұзындығы оның жартысына тең
А
В
С
M
N
1
2
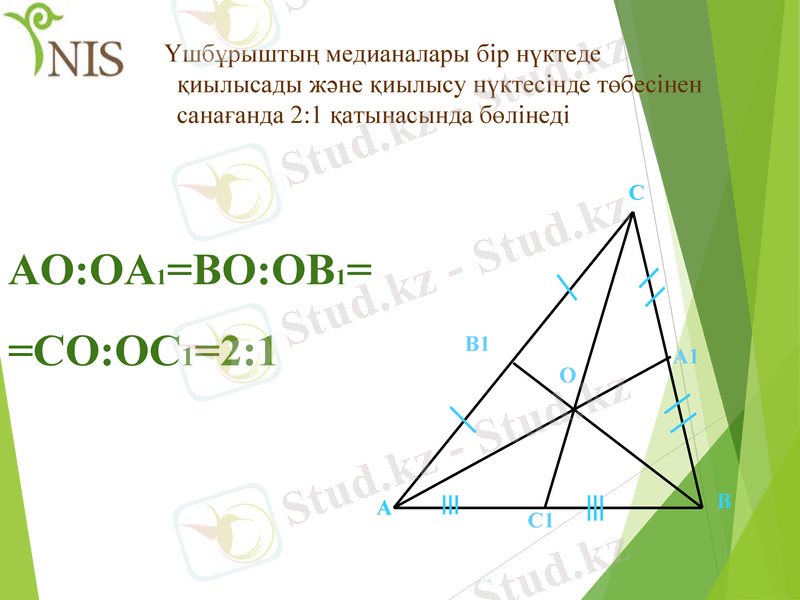
Үшбұрыштың медианалары бір нүктеде қиылысады және қиылысу нүктесінде төбесінен санағанда 2:1 қатынасында бөлінеді
А
В
С
С1
В1
А1
О
АО:ОА1=ВО:ОВ1=
=СО:ОС1=2:1
Тікбұрышты үшбұрыштың тік бұрышынан гипотенузаға түсірілген биіктік оны







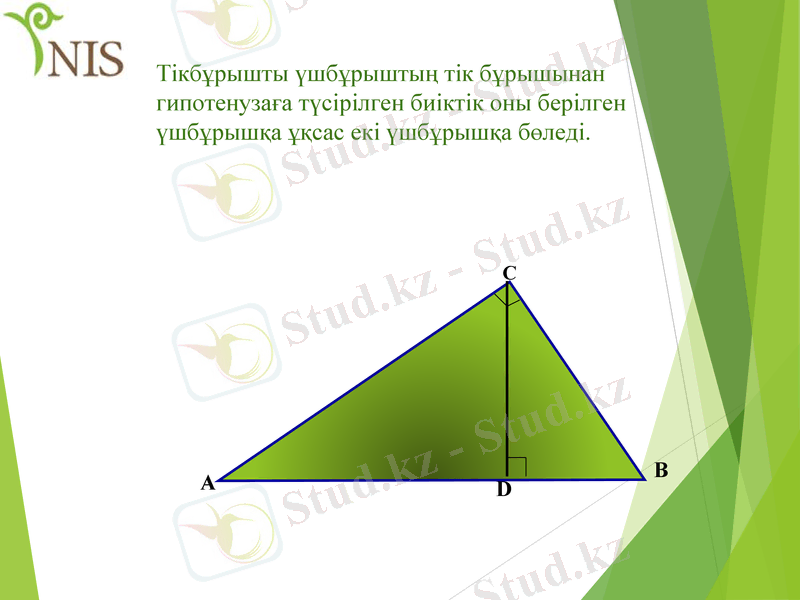
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz