Сыбайлас және вертикаль бұрыштар: анықтамалары мен қасиеттері



Сыбайлас және вертикаль бұрыштар
Сабақ тақырыбы

7. 3. 2. 2
сыбайлас және вертикаль бұрыштар анықтамаларын біледі, оларды анықтай және кескіндей алады;
7. 3. 2. 3
вертикаль және сыбайлас бұрыштардың қасиеттерін қолданады.
Сыбайлас және вертикаль бұрыштар анықтамалары мен қасиеттерін біледі, оларды анықтай және кескіндей алады.
Оқу мақсаттары
Сабақ
мақсаттары

Оқушы
Сыбайлас және вертикаль бұрыштарын ажыратады;
Сыбайлас және вертикаль бұрыштардың анықтамасы мен қасиеттерін қолданады;
Сыбайлас және вертикаль бұрыштардың қасиеттерін қолданып, бұрыштың градустық өлшемін табады;
Дәлелдеу үшін сыбайлас және вертикаль бұрыштардың қасиеттерін пайдаланады.
Бағалау критерийлері:

Қайталау сұрақтары:
Бұрыш ұғымына байланысты сұрақтар (білімді жандандыру) :
Геометриялық фигура - бұрыштың анықтамасы.
Бұрыштың қандай түрлері бар?
Сүйір бұрыш деп қандай бұрышты айтады?
Қандай бұрышты доғал бұрыш деп айтады?
Қандай бұрышты тік бұрыш деп айтады?
Тік бұрыш деп қандай бұрышты айтады?
Бұрыштың өлшем бірлігі.
Бұрышты қандай құралмен өлшейді?
Бұрышты өлшеу қасиеттері (аксиомалар) .
Қандай бұрыштарды тең бұрыштар деп айтамыз?

Жаңа сабақты меңгерту
Балалар, бәріміз дәптерімізге сүйір бұрыш салайық. Осы сүйір бұрыштың бір қабырғасын созайық. Сонда неше бұрыш пайда болды?
Осы пайда болған бұрыштарды сыбайлас бұрыштар деп атайды.

Анықтама: Егер екі бұрыштың бір қабырғасы ортақ, ал қалған екі қабырғалары толықтауыш сәулелер болып келетін екі бұрыш сыбайлас бұрыштар деп аталады.
О - бас нүкте, ОВ - ортақ қабырға.
ОА, ОС қабырғалары - бір -біріне толықтауыш сәулелер.
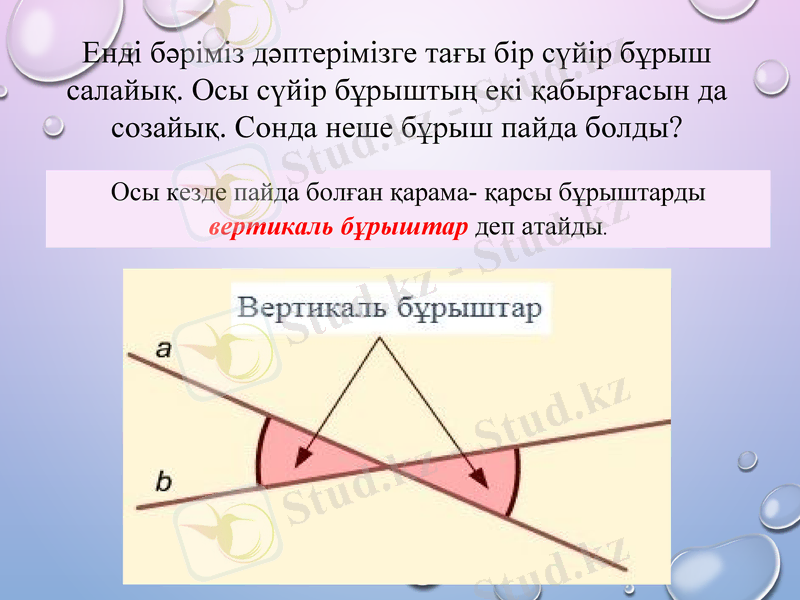
Енді бәріміз дәптерімізге тағы бір сүйір бұрыш салайық. Осы сүйір бұрыштың екі қабырғасын да созайық. Сонда неше бұрыш пайда болды?
Осы кезде пайда болған қарама- қарсы бұрыштарды вертикаль бұрыштар деп атайды.
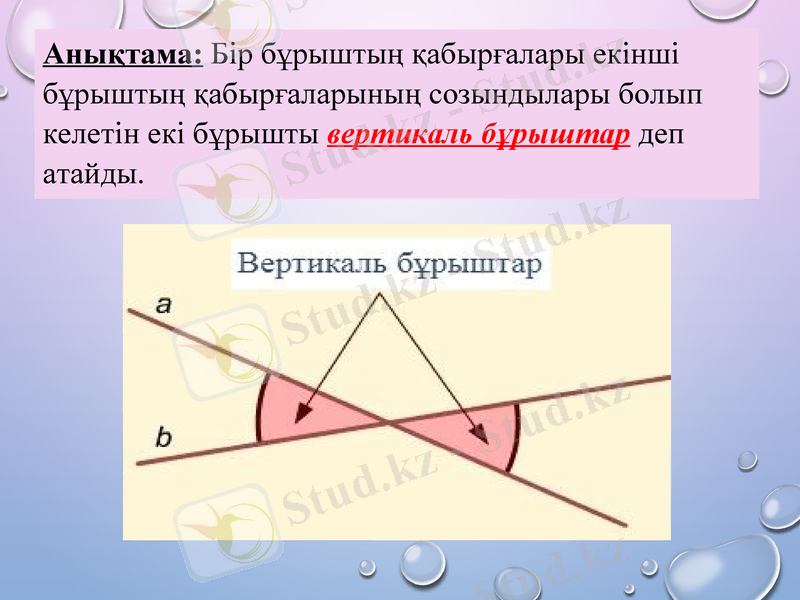
Анықтама: Бір бұрыштың қабырғалары екінші бұрыштың қабырғаларының созындылары болып келетін екі бұрышты вертикаль бұрыштар деп атайды.

Назар аударыңыз!!! Екі түзу қиылысқанда, екі жұп вертикаль бұрыш пайда болады.
1 және 3 бұрыштар
2 және 4 бұрыштар
Вертикаль бұрыштар

Сыбайлас және вертикаль бұрыштардың қасиеттері
Сыбайлас бұрыштардың қасиеттері
Вертикаль бұрыштардың қасиеттері
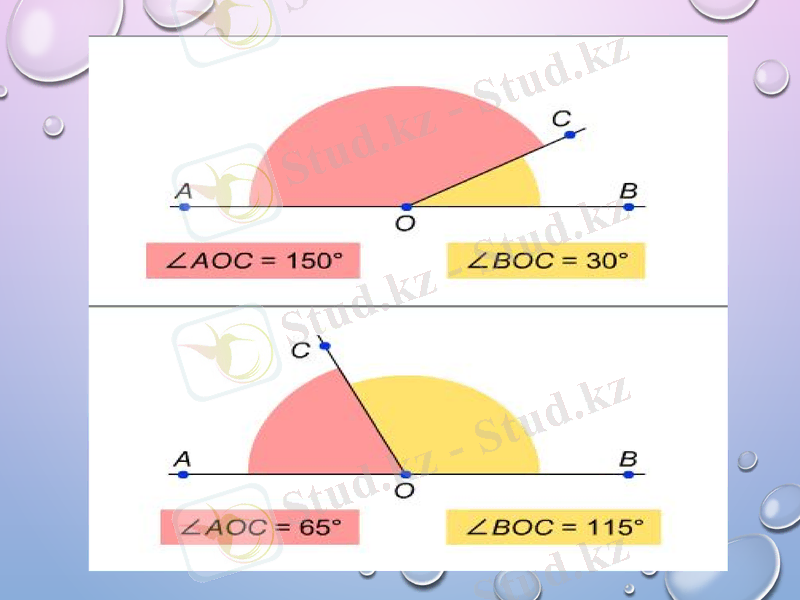
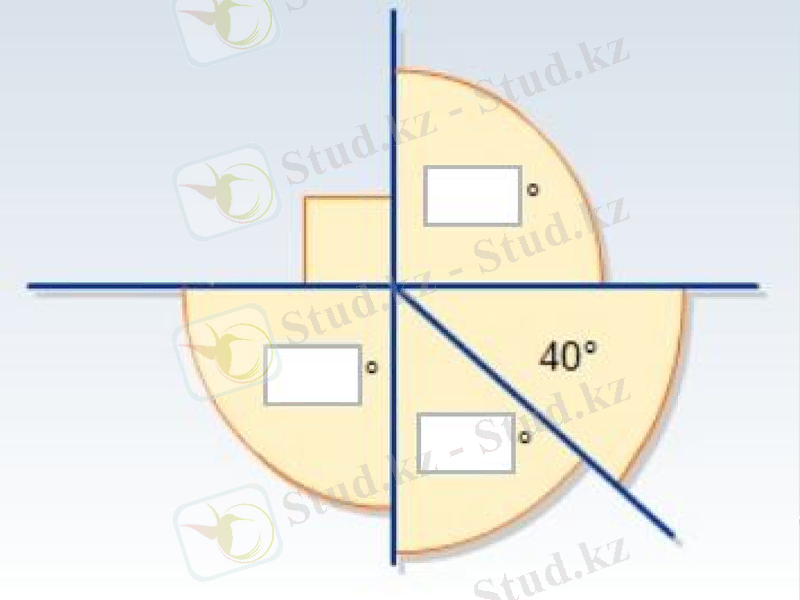
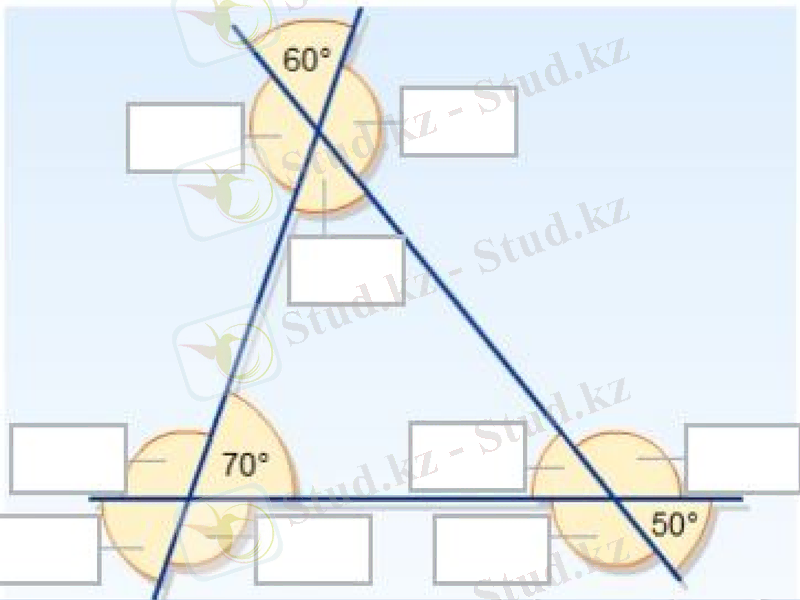
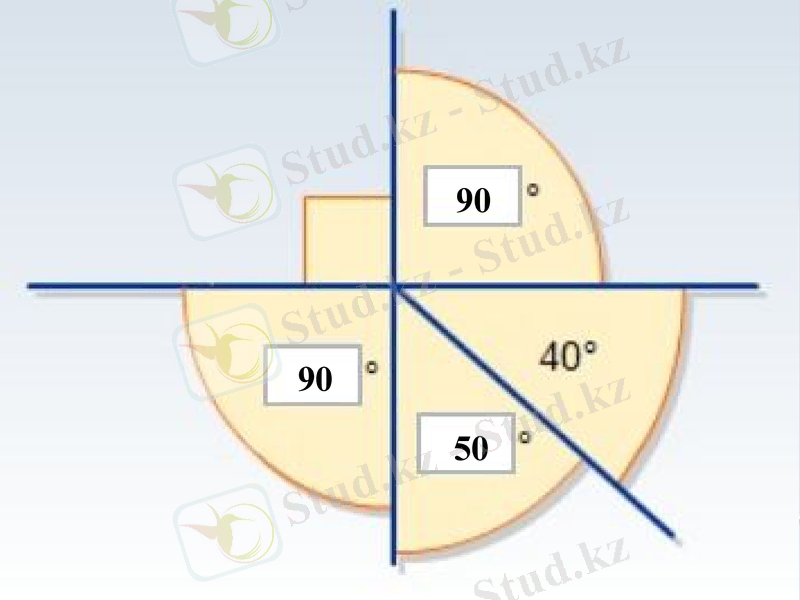
ТАПСЫРМА:
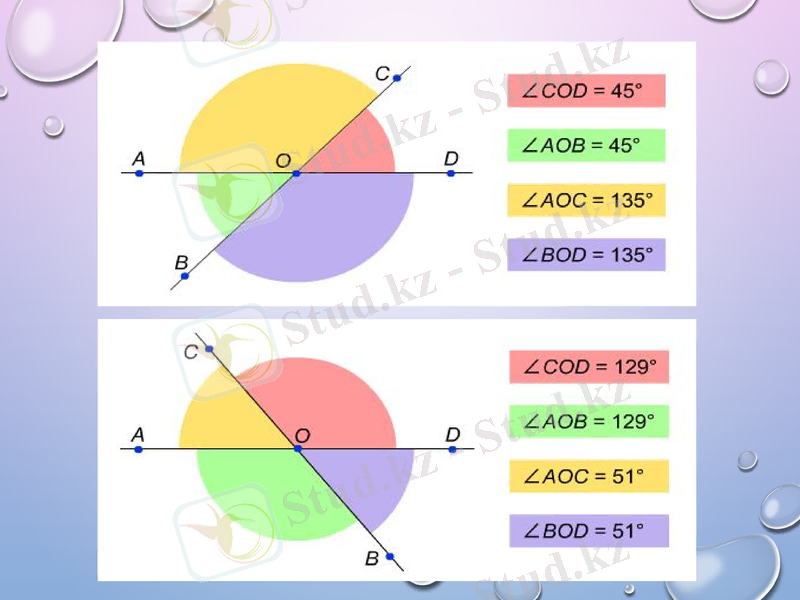
Берілген суреттегі бұрыштардың градустық өлшемдерін ТРАНСПОРТИР көмегімен өлшеп, қорытынды жасаңыздар.
қорытынды
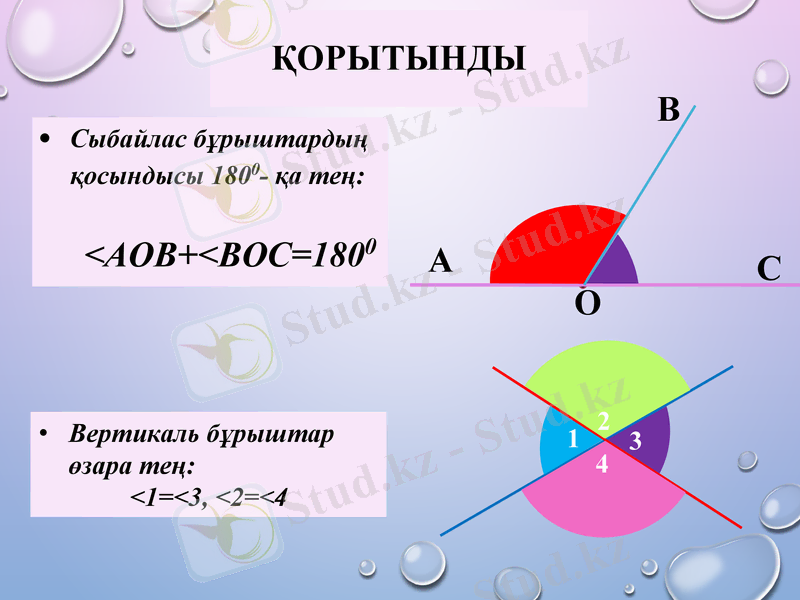
Сыбайлас бұрыштардың қосындысы 1800- қа тең:
Вертикаль бұрыштар өзара тең:
<1=<3, <2=<4
Күнделікті өмірмен байланыс
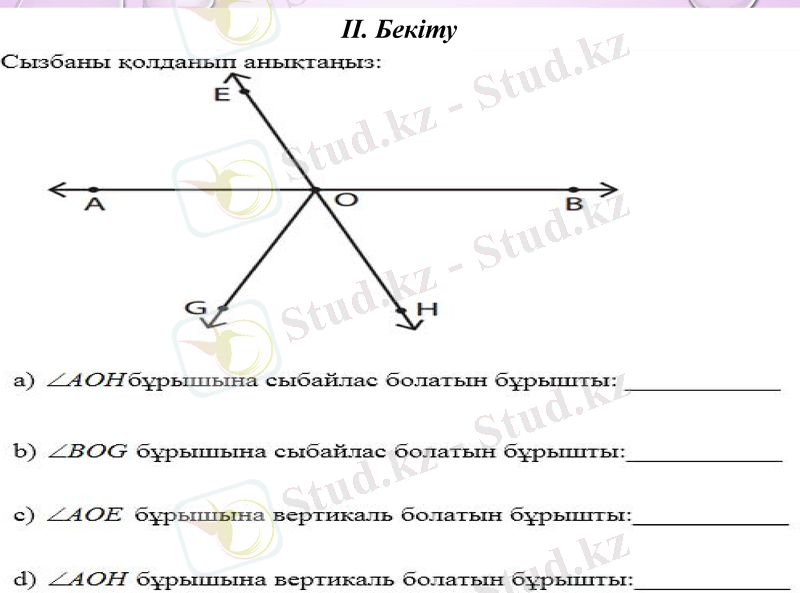
II. Бекіту
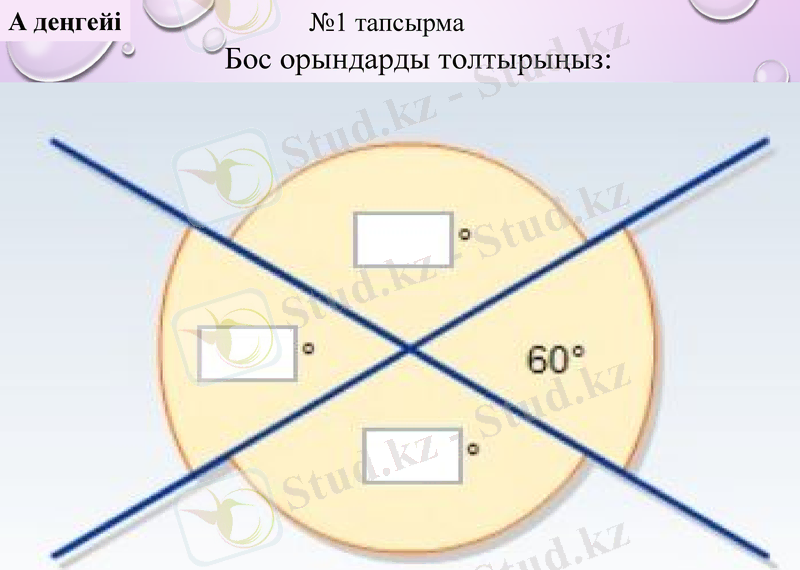
Бос орындарды толтырыңыз:
№1 тапсырма
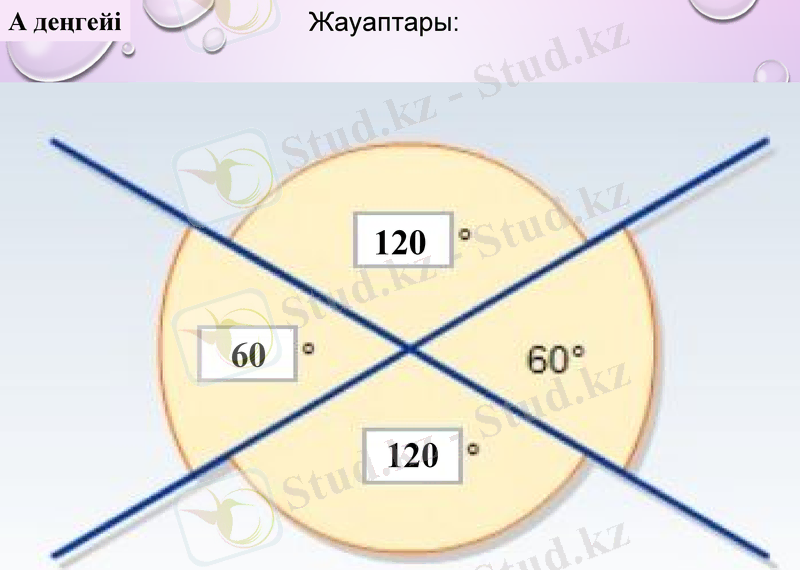
А деңгейі
В деңгейі
3-тапсырма
Төмендегі суретте О нүктесінде қиылысатын үш түзу бейнеленген. <1+<2+<3=1800 болатындығын дәлелдеңіз.
С деңгейі
Жауаптары:
А деңгейі
В деңгейі 1- тапсырма:69 о, 111 о, 69 о, 111о. 2- тапсырма: 45 о, 135 о, 45 о, 135 о. С деңгейі <3=<4(вертикаль бұрыштар) <1+<4+<2=180o => <1+<2+<3=180o (планиметрияның 5 аксиомасы- әрбір бұрыштың нөлден үлкен градустық өлшемі болады. Жазыңқы бұрыштың шамасы 1800 -қа тең. Бұрыштың градустық өлшемі осы бұрыштың қабырғаларының арасы арқылы өтетін кез келген сәулемен бөлінетін бөліктерінің градустық өлшемдерінің қосындысына тең)
Рефлексия
Жетістік критерийлері
жеттім
талпындым
1. Сыбайлас және вертикаль бұрыштарын ажыратады;
2. Сыбайлас және вертикаль бұрыштардың анықтамасын біледі;
3. Сыбайлас және вертикаль бұрыштардың қасиеттерін біледі;
4. Сыбайлас және вертикаль бұрыштардың қасиеттерін қолданып, бұрыштың градустық өлшемін табады.
Үйге тапсырма: № 6. 25-6. 27











- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz