Презентациялар

Гармоникалық тербелістердің дифференциалдық теңдеуі

11-лекция

Гармониялық тербелістердің жалпы сипаттамалары. Гармониялық тербелістердің дифференциалдық теңдеуі.

Тербелістер

Тербелістер деп белгілі бір қайталауға ие қозғалыстар немесе процестер аталады.

Синус (косинус) Заңы бойынша болатын тербелістер гармоникалық деп аталады .

Ψ шамасының гармоникалық тербелістерін келесі теңдік сипаттайды

Ψ (t) = Acos(t+ 0) .

Гармоникалық тербелістер серпімді немесе квазисерпімді күштің әсерінен болады. Бұл күштер пропорционалды және тепе-теңдік жағдайына бағытталған, яғни Гук заңына бағынады:

F(x) = - kx,

мұндағы k - серпімділік коэффициенті.

Жүйеде пайда болатын тербелістер еркін деп аталады, егер ол қысқа мерзімді әсердің нәтижесінде тепе-теңдік жағдайынан шығарылса және одан кейін өз еркіне ие болса.

Егер мұндай жүйенің ауытқуы ішкі күштердің әсерінен ғана орын алса, олар әдетте серпімді немесе квазисерпімді, онда мұндай тербелістер өздік деп аталады. Нақты жағдайларда еркін тербелістер өшетін тербелістер болып табылады, өйткені олар әртүрлі қарсылық күштерінің әсерінен болады.

Сыртқы мерзімдік мәжбүр күштің әсерінен болатын тербелістер еріксіз деп аталады .

Тербелістің сыртқы әсерінің сипаты бойынша еркін және мәжбүрлі болады.

Гармоникалық тербелістер параметрлері Ψ (t) = Acos(0t+ 0)

Ψ - гармоникалық заң бойынша өзгеретін жалпыланған параметр;

А - тербелістердің амплитудасы, тең мағынадан Ψ параметрінің ең үлкен ауытқуы;

(0t+ 0) - тербеліс фазасы;

0 - бастапқы фаза;

0 - меншікті циклдік тербелістер жиілігі, 2 π секунд уақыт ішінде тербелістер саны;

 - тербелістердің сызықтық жиілігі, уақыт бірлігіндегі тербелістер саны; 0 = 2, ωο = dφ/dt

Т - тербеліс периоды, бір толық тербеліс уақыты;

Т = 1/  = 2 / 0

Гармоникалық тербелістердің кинематикасы

Ψ (t) = Acos(0t+ 0)

Тербелмелі бөлшектердің жылдамдығы

υ = = -A0sin(0t+ 0) = A0 cos(0t+ 0+/2)

Тербелмелі бөлшектердің үдеуі

a = = -A02cos(0t+0) = A02 cos(0t+0+)

а = - 02Ψ

Гармоникалық тербелістердің дифференциалдық теңдеуі

Гармоникалық тербелістердің дифференциалдық теңдеуі:

Оның шешімі Ψ = Acos(0t+0)

а+ω02Ψ=0 или:

k

Fупр

m

х

Серіппелі маятник

Х

ma = - kx,

где k/m = ω02,

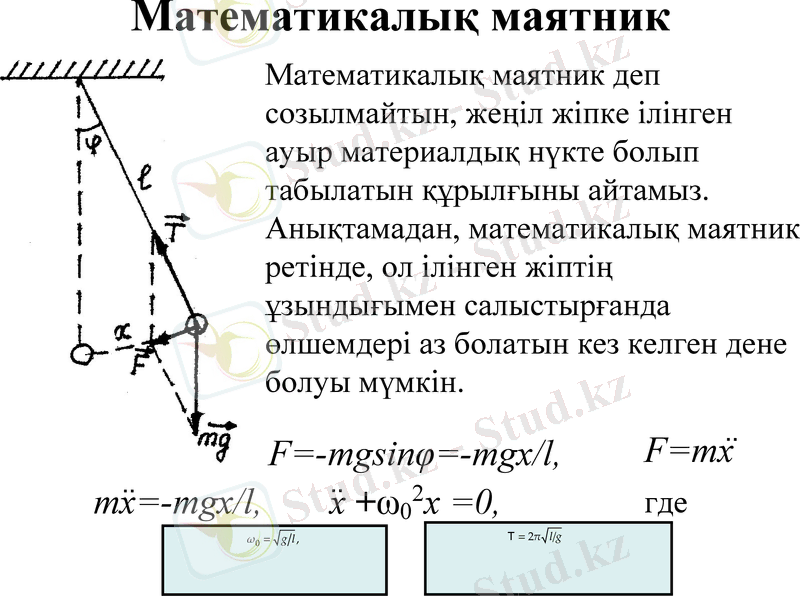
Математикалық маятник

Математикалық маятник деп созылмайтын, жеңіл жіпке ілінген ауыр материалдық нүкте болып табылатын құрылғыны айтамыз.

Анықтамадан, математикалық маятник ретінде, ол ілінген жіптің ұзындығымен салыстырғанда өлшемдері аз болатын кез келген дене болуы мүмкін.

F=-mgsinφ=-тgx/l,

где

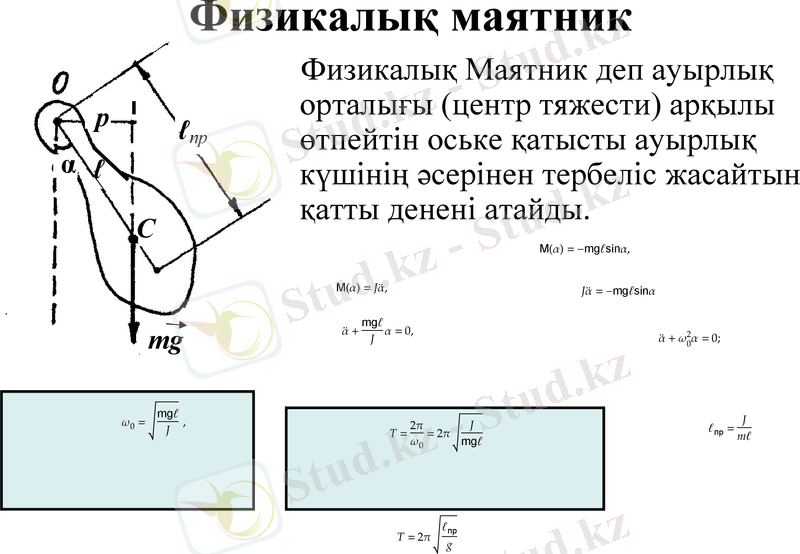
Физикалық маятник

Физикалық Маятник деп ауырлық орталығы (центр тяжести) арқылы өтпейтін оське қатысты ауырлық күшінің әсерінен тербеліс жасайтын қатты денені атайды.

.

Ұқсас жұмыстар

ТОЛҚЫН ТЕҢДЕУІ

Тербеліс түрлері

Еркін өшетін тербелістердің дифференциалдық теңдеуі және оның шешімі

Тербелмелі контур

ГАРМОНИКАЛЫҚ ТЕРБЕЛІСТЕР

Бейсызықты автоматты басқару жүйелері

Дыбыс биіктігі

Материялық нүктенің түзу сызықты тербелістері

Біртекті және біртекті емес коэфиценнті тұрақты екінші ретті сызықтық дифференциалдық теңдеулер

Дыбыс. Дыбыстың сипаттамалары

Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

Ақпарат

Қосымша

Email: info@stud.kz