Тура және кері дирекциондық бұрыштар

Жер ресурстарын басқару, сәулет және дизайн факультеті

Пән: ГЕОДЕЗИЯ

Оқыту бағдарламасы: «Геодезия және картография»

Білім беру бағдарламасының тобы: В074-«Қала құрылысы, құрылыс жұмыстары және азаматтық құрылыс»

Дайындау бағыты: 6В073-«Сәулет және құрылыс»

Білім беру саласы: 6B07 -«Инженерлік, өндеу және и құрылыс саласы»

«Жергеорналастыру және геодезия» кафедрасы

Оқытушы туралы мәліметтер: Капасова Айзада Зарлыковна- т. ғ. к, «Жергеорналастыру және Геодезия» кафедрасының аға оқытушысы, ЖРБСжД факультеті, (каб. 6113), байланысу телефон: 39-79-47; 8-700-669-75-34; идентиф. номер ZOOM № 427-809-09-13; пароль 1953, электрондық почта kapasova_77@mail. ru

Триместр апталары

Барлығы

Дәрістер

ЗЖ

СОӨЖ

СӨЖ

Барлығы

150

ПӘН БОЙЫНША ОҚУ УАҚЫТЫН ШАМАМЕН БӨЛУ

ӘДЕБИЕТТЕР ТІЗІМІ

Негізгі әдебиеттер:

Нурпеисова М. Б. Геодезия. - Оқулық. -Алматы: Эверо, 2015. -276 б.

Г. Г. Поклад, С. П. Гриднев. Геодезия: учебное пособие для вузов. - М. : Академический проект, 2017. -592с.

Игильманов Ж. А., Кусаинова Г. Д., Игильманов А. А. Геодезия. - Оқу құрал. - Астана, 2013-145с.

Капасова А. З. Геодезия. - Оқу құрал. -Қарағанды, 2014. -120 б.

Кочетова Э. Ф., Акрицкая И. И., Л. Р. Тюльникова, А. Б. Гордеев Н. Инженерная геодезия: учебное пособие. Новгород: ННГАСУ, 2017. - 158 с.

Қосымша әдебиеттер:

Инструкция по топографической съемке в масштабах 1:5 000, 1:2000, 1:1000, и 1:500. http://www. racurs. ru/

Инструкция по топографической съемке в масштабах 1:5 000, 1:2000, Москва, ЦНИИГАиК.

Условные знаки для топографических планов масштабов 1: 5000, 1:2000, 1:1000, 1:500. http://geo-fond. ru/docs/uz-top. pdf

4-Дәріс

Сызықты бағдарлау. Тура және кері геодезиялық есептер. (2-сағ)

Дәріс жоспары:

1. Сызықтарды негізгі және магниттік меридиандар бойынша бағдарлау

2. Сызықтарды осьтік меридиан бойынша бағдарлау

3. Румбтар және олардың дирекциондық бұрыштармен байланысы

4. Келесі сызықтың дирекциондық бұрышын анықтау

5. Тура және кері геодезиялық есептер

1 Сызықтарды негізгі және магниттік меридиандар бойынша бағдарлау

Жер бетінде орналасқан заттарды, сызықтарды бағдарлау дегеніміз, олардың меридианнан бастап есептелген бағытын анықтау. Бағдарлау кезінде негізгі тұрақты бағыт географиялық, магниттік меридиан, сондай-ақ, осьтік меридиан (Х-осі) немесе оған параллель сызықтар да алынады. Жергілікті жердегі заттарды компас немесе буссоль арқылы бағдарлауға болады. Компастың (буссольдың) шеңбері 360°-қа бөлінеді. Меридианның солтүстік басынан бір затқа қарай сағат тілінің бағытымен есептелген жергілікті немесе картадағы горизонталь бұрышты азимут деп атайды, ал азимут арабшадан аударғанда «бағытты» білдіреді.

Берілген бір нүктеде меридианды астрономия тәсілімен тапсақ, онда меридиан негізгі (географиялық), ал магнит стрелкасы арқылы тапсақ, магниттік меридиан болып аталады.

Осыған сәйкес өлшенетін азимутта негізгіАн және магниттікАмаг азимут болып келеді. Әр нүктенің магниттік меридианы оның географиялық негізгі меридианына сәйкес келмейді (19, б-сурет), олардың арасындағы бұрыш магнит стрелкасының бұрылу бұрышы (δ) деп аталады. Егер стрелканың солтүстік ұшы негізгі меридианнан шығысқа қарай бұрылса, шығыстық бұрылу оң (+), батыстық бұрылу бұрышы болса, онда батыстық бұрылу теріс (-) болып келеді. Егер магнит тілінің бұрылу бұрышы δ-ның мәні белгілі болса, магниттік азимуттан негізгі азимутқа мына төмендегі формуланы пайдаланып, көшуге болады:

(9)

мұндағы δ ш,, δ6 - магнит тілінің шығыс және батыс бұрылулары.

Шығыс бұрылуды оң (+), ол батыс бұрылуды теріс (-) деп қабылдаймыз.

Магнит тілінің бұрылуы жер бетінің әр жерінде әртүрлі болып келеді. ТМД елдерінде δ-ның шамасы 0°-тан 20°-ға жуық шамаға екі жаққа ауытқиды. Демек, сызықтарды магниттік меридиан бойынша бағдарлау тек қана жер бетінің шағын учаскелерінің пландарын жасағанда ғана қолданылады.

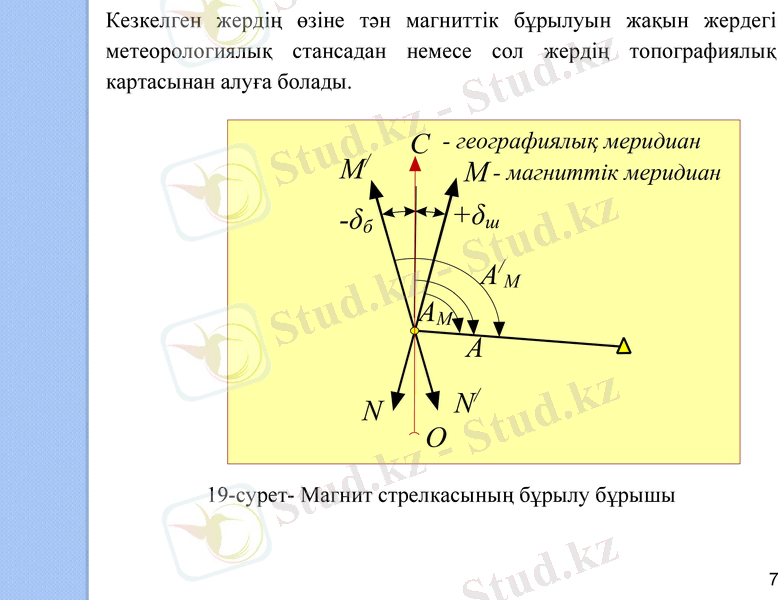
Кезкелген жердің өзіне тән магниттік бұрылуын жақын жердегі метеорологиялық стансадан немесе сол жердің топографиялық картасынан алуға болады.

19-сурет- Магнит стрелкасының бұрылу бұрышы

2 Сызықтарды осьтік меридиан бойынша бағдарлау

Карталар мен пландар координаталардың зоналық тік бұрышты жүйесінде жасалатындықтан, геодезияда дирекциондық бұрыштар жиі қолданылады. Дирекциондық бұрыш () деп осьтік меридианның солтүстік жағынан сағат тілінің бағытымен бағдарланғыш сызыққа дейінгі горизонталь бұрышты айтады. Дирекциондық бұрыштар азимуттар сияқты 0°-тан 360°-қа дейін өзгереді.

Бағдарланып отырған сызықтың дирекциондық бұрышы азимуты сияқты тура және кері бола алады және бір-бірінен 180-қа айырмашылығы болады (20- сурет) .

20- сурет- Тура және кері дирекциондық бұрыштар

Ал жалпы жағдайда:

Геодезиялық өлшеулердің барлығы да сызықтар дирекциондық бұрыштар арқылы бағдарланады, өйткені сызықтың дирекциондық бұрышы жер бетінің кезкелген нүктесінде өз мәнін өзгертпейді, яғни тұрақты. Бұлдирекциондық бұрыштың азимутқа қарағандағы бір ерекшелігі. Ал, тура және кері азимуттар арасындағы байланысты мына формулада көруге болады:

Акері=Атура+180+γ, мұндағы γмеридиандардың жақындасу бұрышы; яғни меридиан мен осьтік меридиан (х) немесе оған параллель сызық арасындағы бұрыш. Бұл бұрыштың мәні әр нүктенің О-дік меридианнан қашықтауына байланысты ауытқып отырады. 21-сурет бойынша АВ сызығының негізгі азимуты Ан, ал дирекциондық бұрышы αАВ десек, онда:

γ=АВ-Ан,

яғни, нақты бір нүктедегі кез келген сызықтың негізгі азимутымен дирекциондық бұрышының айырмашылығы (γосы нүктедегі негізгі меридиан мен осьтік меридианның жақындасуына тең.

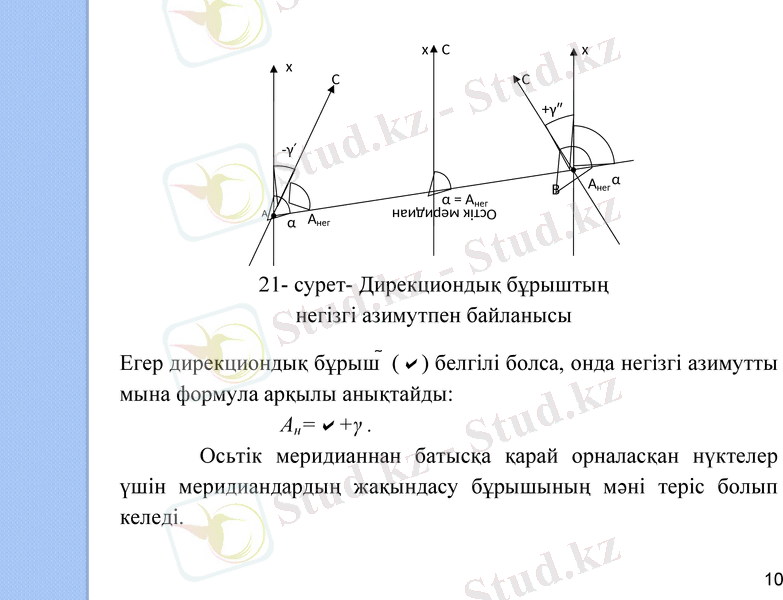
Егер дирекциондық бұрыш  () белгілі болса, онда негізгі азимутты мына формула арқылы анықтайды:

Ан=+γ . Осьтік меридианнан батысқа қарай орналасқан нүктелер үшін меридиандардың жақындасу бұрышының мәні теріс болып келеді.

3. Румбтар және олардың дирекциондық бұрыштармен байланысы

Сызықтарды бағдарлау және өлшеу нәтижелерін өңдеу кезінде румб деп аталатын сүйір бұрыш пайдаланылады. Шамасы 0°-тан 90°-қа дейін өзгеретін осьтік меридианның солтүстік не оңтүстік жағынан екі жаққа қарай бір нақты сызыққа дейін есептелетін сүйір бұрышты румб дейді.

22-суретте әр ширекте алынған төрт сызықтың румбтары көрсетілген. Бағытты румб арқылы табу үшін оның сан мәнінің алдына ширектің аты көрсетіледі. Мысалы, СШ (солтүстік-шығыс), ОШ (оңтүстік-шығыс), ОБ (оңтүстік-батыс), СБ (солтүстік-батыс) деп белгіленеді және осы суреттен әрбір ширекте румбтар (таблицалық бұрыштар) мен дирекциондық бұрыштар арасындағы байланысты көруге болады. Ол байланыс формулалары 4-кестеде берілген.

Дирекциондық бұрыштарды румбтарға (таблицалық бұрыштарға) аударғанымыз, тригонометриялық функциялардың 0°-ден 90° аралығындағы таблицалық нақтылы мәндерін пайдалануға мүмкіндік береді.

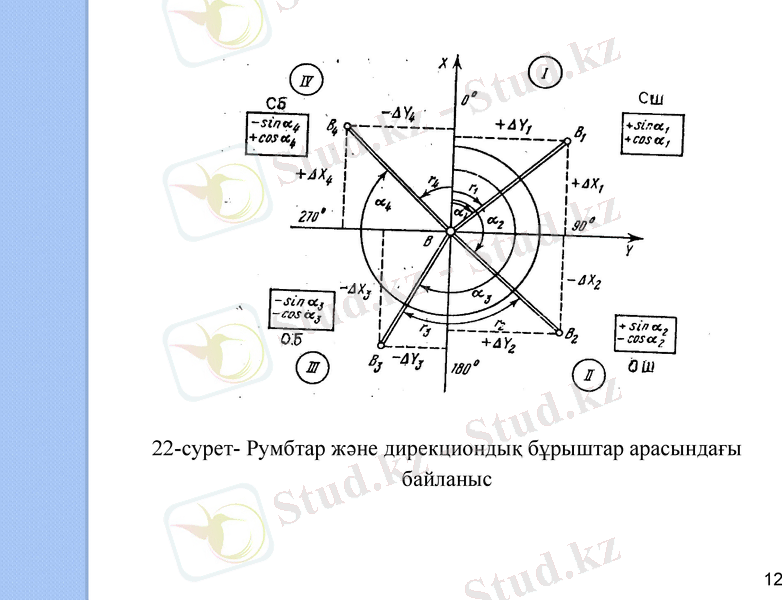
22-сурет- Румбтар және дирекциондық бұрыштар арасындағы байланыс

Ширектер нөмірлері

Дирекциондық бұрыштардың өзгеруі аралықтары

Румбтардың аттары

Байланыс формалары

00 ≤  ≤ 90

СШ

r1 = 1

900 ≤ 2 ≤ 1800

ОШ

r2 =180-2

III

1800 ≤ 3 ≤ 270°

ОБ

r3 =3 -180

2700 ≤ 4 ≤ 3600

СБ

r4 =360-4

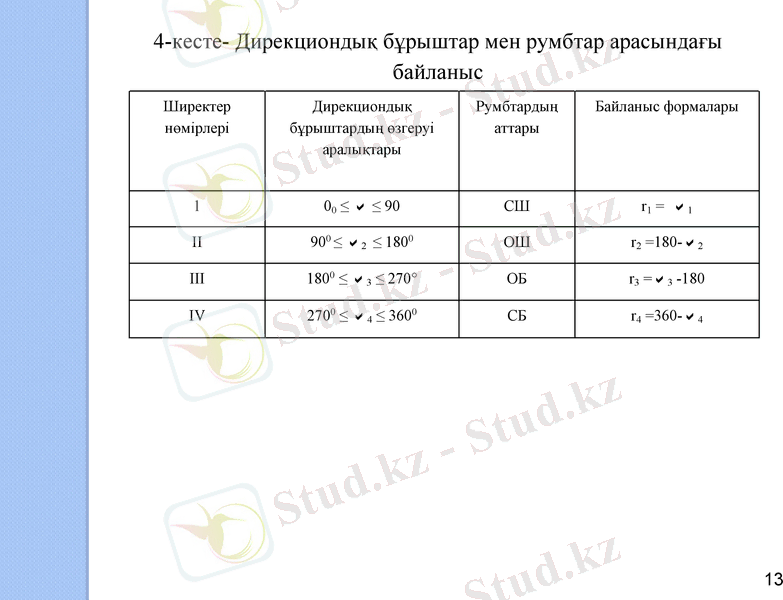
4-кесте- Дирекциондық бұрыштар мен румбтар арасындағы байланыс

4 Келесі сызықтың дирекциондық бұрышын анықтау

Полигонды теодолиттік жүрісте жер беті мен жер астында горизонтальды (оң немесе сол) бұрыштар өлшенеді. Дирекциондық бұрыштар мен полигон бұрыштары арасындағы байланыс 23, а, б- суреттерінде көрсетілген.

Жалпы жағдайда дирекциондық бұрыштарды келесі формулалармен есептейді:

а) жүрістің оң жағындағы горизонталь өлшенген бұрыштар үшін

(I4)

б) жүрістің сол жағындағы горизонталь өлшенген бұрыштар үшін

(I5)

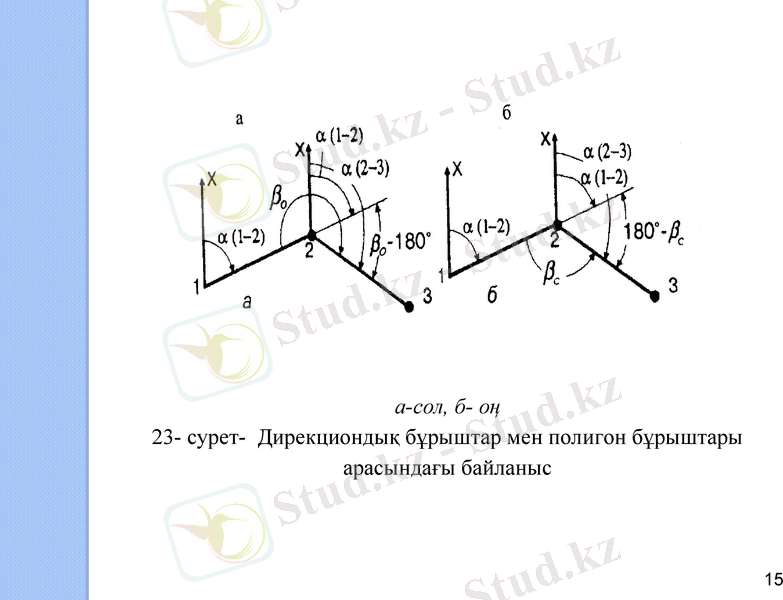
а-сол, б- оң

23- сурет- Дирекциондық бұрыштар мен полигон бұрыштары арасындағы байланыс

5 Тура және кері геодезиялық есептер

Геодезиялық және маркшейдерлік жұмыстарда пункттер координаталары, олардың арақашықтықтары мен дирекциондық бұрыштары тікелей немесе кері геодезиялық есептерді шешу арқылы анықталады.

Тура геодезиялық есеп. Егер координаталары белгілі А пунктінен, екінші В пунктіне дейінгі арақашықтық d және дирекциондық бұрыш аАВ белгілі болса, онда В пунктінің координаталарын табуға болады. Координаталардың бір пунктте осылайша берілуін тура геодезиялық есеп деп атайды. АВ полигонның бір қабырғасы, оның жазықтағы проекциясы d, ал дирекциондық бұрышы АВ делік (24-сурет) .

Бастапқы А нүктесінің (ХА, УА) координаталары белгілі де, шарт бойынша В-нүктесінен (ХА, УА) координаталарын (Хв, Ув) анықтау керек. 24-сурет бойынша:

мұндағы Δх пен Δу-координата өсімшесі деп аталады. Тік бұрышты үшбұрыш АВС-дан Δх -пен Δу былайша анықталады:

Тексеру:

Координаталар өсімшелері Δх пен Δу-тің таңбалары соs  мен sin -ға байланысты оң және теріс болып келеді. Дирекциондық бұрыш -ның әртүрлі мағынасына сәйкес Δх пен Δу таңбаларының өзгеруі 5-кестеде көрсетілген.

Координаталар өсімшелері

Ширектер

І-СШ

ІІ-ОШ

ІІІ-ОБ

IV-СБ,

Δх

Δу

5-кесте-Координаталар өсімшелерінің ширектегі таңбалары

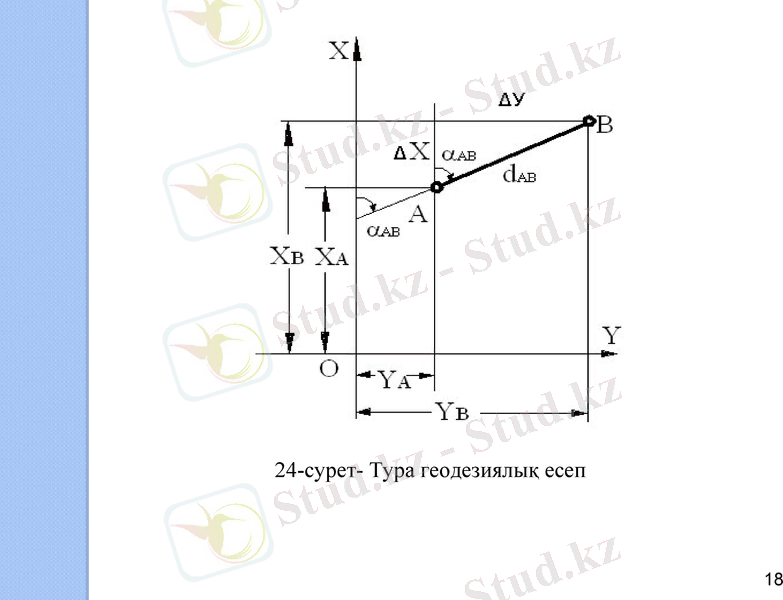
24-сурет- Тура геодезиялық есеп

Анықталған өсімшелер Δх пен Δу арқылы екінші В пунктінің координаталары есептелінеді:

ХВ=ХА+Δх,

YВ=YА+Δу.

Координаталардың бастапқы пункттен екінші пунктке осылайша берілуін тура геодезиялық есеп деп атайды.

Кері геодезиялық есеп. Координаталары белгілі екі пункт 1 және 2 арқылы 1-2 түзуінің дирекциондық бұрышы 1-2 және ұзындығы d1-2 анықтау керек болған жағдайда, кері геодезиялық есеп деп аталатын тәсіл қолданылады X1Y1 Х2, Y 2-1 және 2 пункттерінің координаталары.

25-суретте координаталар өсімшелері былайша анықталады:

ΔХ=Х2-Х1,

Δу=У2-У1.

Ал таблицалық бұрыш (румб) 1-2-1 үшбұрышынан анықталады:

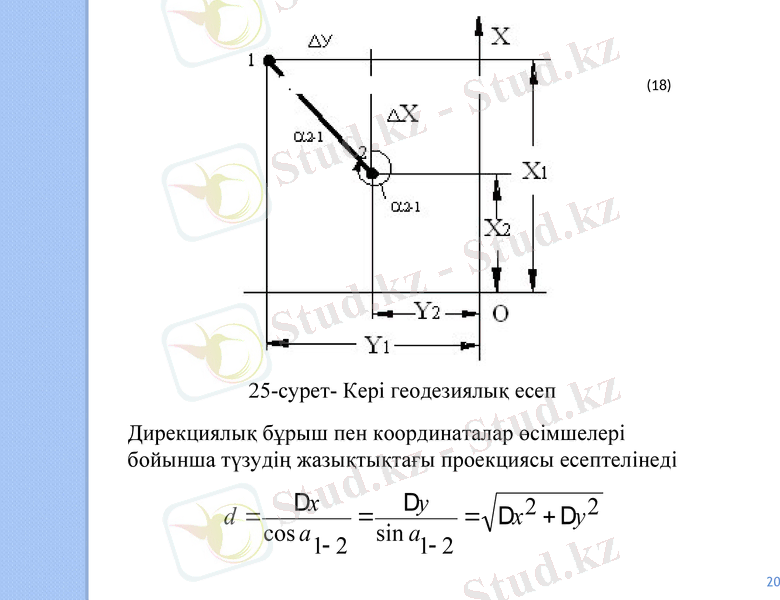
25-сурет- Кері геодезиялық есеп

Дирекциялық бұрыш пен координаталар өсімшелері

бойынша түзудің жазықтықтағы проекциясы есептелінеді

. (18)

СӨЖ тақырыб бойынша тестке дайындық: 4-Дәріс Сызықты бағдарлау. Тура және кері геодезиялық есептер

1. Жердің бедері және оны пландар мен карталарда бейнелеу

(Конспект жазу)

28 Координаталар өсімшесін келесі формуланың қайсысымен есептеледі :

А)  d cos ,  d sin  ;

В)  d sin ,  d cos  ;

С)  Xn-1 - X,  Yn-1 - Y

D)  D cos 2,  D sin 2 ;

Е)  d tg ,  d ctg  .

33 Гаусс - Крюгер проекциясындағы жазық тік бұрышты координаталар жүйесінде ординатаға жазылады:

A) меридиандар мен параллелдер сызығынан

B) километрлік торлар сызығынан

C) 60 зоналардың номері

D) нүктелер арасындағы сызықтардан

E) геодезиялық сызықтардан

63 Румбаның (кесте бұрыш) мәнін анықтаңыз, егер бағыттың дирекциондық бұрышы =29125

А) r = 29125;

В) r = 6835;

С) r = 2125;

D) r = 125;

Е) r = 9135.

64 Сағат тілі бағытымен берілген бағытқа дейінгі есептелетін горизонталь бұрыш дирекционды бұрыш деп аталады. Бастапқы бағыты:

A) ОХ өстік меридианының оңтүстік бағытынан;

B) ОХ өстік меридианның солтүстік бағытынан;

C) шын меридианның оңтүстік бағытынан;

D) шын меридианның солтүстік бағытынан;

E) магниттік меридианның солтүстік бағытынан.

67 Дирекциондық бұрышы   25319 бағыты үшін кестелік бұрышты анықтаңыз:

А) r  7319;

В) r  25319;

С) r  1641;

D) r  10641;

Е) r  16319.

68 Тура және кері дирекциондық бұрыштар айырмасы:

A) 2700;

B) 900;

C) 00;

D) 1800;

E) 3600.

70 1-2 сызықтың кері дирекциондық бұрышын анықтау формуласын көрсет.

A) 21 = Амаг. - 

B) 21 = 12  180

C) 12 = 180 - 

D) 21 = А12 - 

E) 12 = 180 - 

71 АВ жағының дирекциондық бұрышы АВ 2314 тең. Кері дирекциондық бұрышты есепте?

A) 135 20

B) 55 25

C) 203 14

D) 85 15

E) 68 25

74 Дирекциондық бұрыштың мәні 100 00. Румбтың мәні неге тең?

A) rОШ = 80 00

B) rСШ = 55 25

C) rОБ = 135 20

D) rСШ = 95 15

E) rОШ = 68 25

77 Дирекциондық бұрыш қандай шартты бағыттан өлшенеді?

A) негізгі меридианнан

Ұқсас жұмыстар

ТУРА ЖӘНЕ КЕРІ АЗИМУТ

Сызықтарды бағдарлау

Теореманы логикалық дидактикалық талдау және теоремамен жұмыс істеу әдістемесі

Полигонометриялық ығысу құжаттары мен журналдары

Бірінші ойыншыны іріктеу сұрағы

Сыбайлас бұрыштар Вертикаль бұрыштар

СЫБАЙЛАС ЖӘНЕ ВЕРТИКАЛЬ БҰРЫШТАРДЫҢ ҚАСИЕТТЕРІ

Үшбұрыштың ішкі бұрыштарының қосындысы. Қайталау сабағы

Параллель түзулерге шынайы өмірден мысалдар

Вертикаль бұрыштар

Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

Ақпарат

Қосымша

Email: info@stud.kz