Дискреттік математика негіздері: жиындар, функциялар, қатынастар және графтар теориясы



Сабақтың тақырыбы: Дискреттік математика негіздері

Жоспары:
Жиындар теориясы
Жиындар және олармен орындалатын амалдар
Функциялар
Қатынастар
Графтар теориясы
Негізгі түсініктері.
Графтың түрлері.
Ағаштар.

Жиын. Негізгі түсініктер
Жиын деп анықталған нысандардың бірге топтасуын айтады.
Жиынның элементі деп жиынның жекеше
нысанын айтады.
Бос жиын деп, құрамында бір де бір элемент жоқ жиынды айтады.
Әмбебап жиын (универсум) U деп, қарастырылған барлық қолданылатын элементтер жиынын айтады

Жиындармен орындалатын амалдар
Біріктіру AB = {x xA xB}
Қиылысу AB = {x xA & xB}
Айырым A\B = {x xA & xB}
Симметриялық айырым
A/B = (AB) \(AB ) = {x (xA & xB) (xA & xB) }
Толықтыру = {x x A} = U\A, мұндағы U - әмбебап жиын.

Біріктіру
А және В жиындарын біріктіру деп А немесе В жиындарының ең болмағанда бірінің құрамына енетін элементтерден тұратын
А В жиынын айтады.
Қасиеттері
1) рефлексивтік А А = A
2) коммутативтік А В = В А
3) ассоциативтік
А (ВС) = (АВ) С = А В С
4) Бос жиынмен біріктіру А = А
5) Әмбебап жиынмен біріктіру А U = U

Қиылысу
А және В жиындарының қиылысуы деп, А немесе В жиындарының құрамына бірдей енетін элементтерден тұратын А В жиынын айтады.
Қасиеттері:
1) рефлексивтік А А = A
2) коммутативтік А В = В А
3) ассоциативтік
А (ВС) = (АВ) С = А В С
4) Бос жиынмен қиылысу А =
5) Әмбебап жиынмен қиылысу А U = А
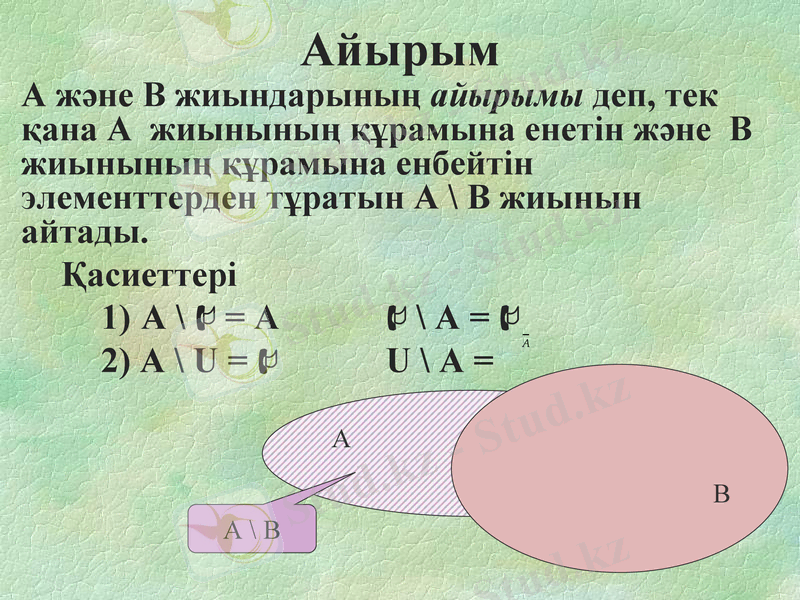
Айырым
А және В жиындарының айырымы деп, тек қана А жиынының құрамына енетін және В жиынының құрамына енбейтін элементтерден тұратын А \ В жиынын айтады.
Қасиеттері
А \ = А \ А =
2) А \ U = U \ А =

Симметриялық айырым
А және В жиындарының симметриялық айырымы деп тек қана А және В жиындарының бірігуінде жататын және олардың қиылысуында жатпайтын элементтерден тұратын жиынды айтады.
Қасиеттері:
1) Коммутативтік А / В = В / А
2) Ассоциативтік А/(В/С) = (А/В) /С =А/В/С
3) А / = А
4) А / U =

Толықтыру
А жиынын әмбебап U жиынмен толықтыру деп, тек қана әмбебап жиынның құрамына енетін және А жиынының құрамына енбейтін элементтерден тұратын жиынды айтады.
Қасиеттері:
А = U А =
U
A

Функциялар
Функция дегеніміз - бір айнымалының өзгеруіне байланысты өзгеріп отыратын шама.
(x1, y1) f және (x2, y2) f
x1 = x2 -ден y1 = y2 шығады.
Кез келген (x, y) f үшін y = f(x), яғни у х-ке тәуелді функция. у-тәуелді, х-тәуелсіз айнымалы
Функция бір немесе бірнеше тәуелсіз айнымалылар арқылы тәуелді айнымалыны көрсететін формулалармен беріледі.
f = { (x, y) XY y = f(x) }
f - (x, y) жұбын анықтайтын сәйкестік
f(x) - xX элементіне сәйкес
yY элементінің белгіленуі

Қатынас
Қатынас деп әр түрлі нысандар қасиетін және олардың арасындағы байланысты анықтайтын математикалық құрылымды айтады.
(Х, R) жиындар жұбын қатынас деп атайды, мұндағы RХn.
Жиында берілетін n-орынды (n-арнды) қатынас деп, жиындардың тура көбейтіндісінің ішкі жиындары аталады

Қатынастар түрлері
Бір орынды немесе унарлы қатынас деп бір айнымалымен орындалатын қатынасты айтады (терістеу амалы, санның дәрежесін табу) .
Екі орынды қатынастарды бинарлы деп атайды және оларды инфиксті жазбамен жазады: хRу. (конъюнкция, дизъюнкция)
Үш орынды қатынастарды тренарлы деп атайды.
“Би” сөзі “екі”, “уно” сөзі “бір” деген мағынаны береді.

Қатынастар қасиеттері
Рефлексивтік
х R х - ақиқат ;
Антирефлексивтік
х R х - жалған;
Симметриялық
х R у у R х ;
Антисимметриялық
(х R у) &(у R х) x=y ;
Сызықтық
Егер (х R у) - ақиқат, онда (у R х) - жалған;
Транзитивтік
(х R у) &(у R z) x R z .

Граф деп өзара байланысқан нысандар жиынтығын айтады. Нысандар-шыңдар деп аталады және нүктелер арқылы белгіленеді. Ал шыңдар арасындағы байланыс-доғалар немесе қабырғалар деп аталады
Граф G = (V, Е) V және Е соңғы жиындар жұбымен беріледі. Бірінші жиын элементтері v1, v2, . . . , v M графтың шыңы деп аталады (графикалық көріністе оларға нүктелер сәйкес) . Екінші жиын элементтері el, e2, . . . , e N қабырғалар деп аталады. Әр қабырға шыңдар жұбымен анықталады (графикалық көріністе қабырғалар графтың екі шыңын қосады) .
Графтар
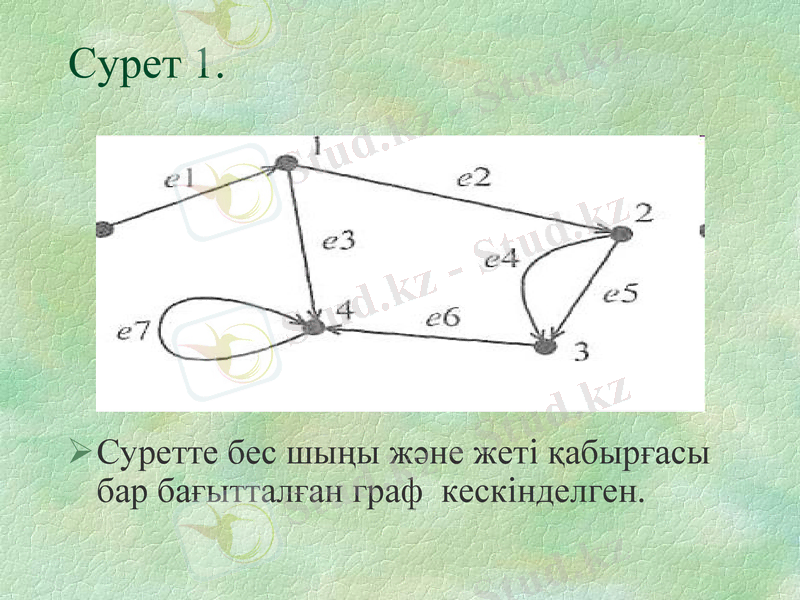
Сурет 1.
Суретте бес шыңы және жеті қабырғасы бар бағытталған граф кескінделген.

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz