Периодты синусоидалық емес токтар мен кернеулер: гармоникалық талдау, пайдалы мәндер, қуат және электрлік фильтрлер


Кіріспе
Қазіргі уақытта электр энергиясы барлық өнеркәсіп салаларында, транспортта, ауыл шаруашылығында, үй тұрмысында, тағы да басқа халықтың тұрмыс қажетіне кеңінен пайдаланылады. Осы курстың негізгі бір міндеті, ол құбылыстарды токтар, кернеулер, қуаттар, магнит ағындары т. б. түсініктер арқылы есептеу, зерттеу. Сондай - ақ тағы бір атқаратын міндеті, ол әрбір құбылыстарды электр кернеулігі, магнит өрісінің индукциясы, қуат ағындары, т. б. түсініктер арқылы есептеу, зерттеу. Осы міндеттердің біріншісі тізбектерді есептеу мен зерттеуге, ал екіншісі электр магниті өрістерін есептеуге, зерттеуге арналған.
Синусиолды тербеліс периодты процестың ең қарапайым формасы болып табылады. Электр энергетикалық жүйе торында айнымалы синусоидалық форманың тоқтарымен қуаттарын бір қалыпты ұстау үшін қолданады. Бірақ, мысалға, электр байланыс тізбегінде, электронды және жартылай өткізгіштік құралдарында синусоидалық форма ауытқуы жиі кездеседі, және де ол шартты түрде жұмыс процессінде анықталады. Сондықтан да синусоидалық емес периодты тоқтың элементтерін білу автоматтық құралдарға, электронды құралдарға және қазіргі заманға сай жаңа әр түрлі аппаратура мен техникалық құралдарды игеру үшін тығыз байланысты.
I Негізгі бөлім
1. 1 Синусоидалық емес токтардың алғы шарттары.
Синусоидалық емес периодтың функциясы мына шартта қанағаттандырылады:
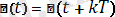
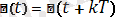 , мұнда Т - функция периоды, яғни қайталануға кеткен процесстің уақыт аралығы, к - бүтін сан.
, мұнда Т - функция периоды, яғни қайталануға кеткен процесстің уақыт аралығы, к - бүтін сан.
Математикадағы курстардан белгілі болған, осындай периодты функция, гармоникалық тізбекте анықталуы мүмкін және жалпы жағдайдағы шексіз, бірақ, электірлік тізбектердегі есептеулер бойынша “n” саны бар шектеумен синусоидалық не гармоника депте атайды. Мысалға, синусионалды емес ток
i=
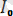
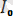 +
+
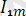
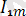 sin(wt+
sin(wt+
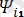
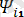 ) +
) +
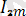
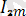 sin(2wt+
sin(2wt+
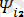
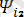 ) +…+
) +…+
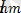
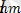 sin(nwt+
sin(nwt+
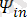
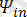 )
)
немесе бұдан
i=
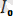
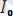 +
+
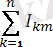
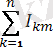 sin(kwt+
sin(kwt+
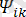
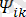 ) .
) .
Бұл формулада
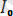
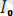 - тұрақты тоқ;
- тұрақты тоқ;
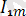
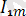 sin(wt+
sin(wt+
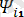
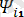 ) - бірінші гармоника, мұнда функция жиілігі синусоидалық емес периодты токка (i) тең. Қалған функциялар жоғары гармоникалар болып табылады;
) - бірінші гармоника, мұнда функция жиілігі синусоидалық емес периодты токка (i) тең. Қалған функциялар жоғары гармоникалар болып табылады;
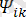
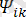 - k-шы гармониканы құрайтын, бастапқы уақытқа (t=0) тәуелді болатын, бастапқы фаза. Осыдан келе, периодты синусоидалық емес токты тұрақты ток пен әр түрлі бастапқы фазаларынан тұратын синусоидалық токтардың жалпы қосындысы деп алсақ болады. Бұндай тұжырымдаманы периодты синусоидалық емес токтарды есептегенде жиі қолданылады.
- k-шы гармониканы құрайтын, бастапқы уақытқа (t=0) тәуелді болатын, бастапқы фаза. Осыдан келе, периодты синусоидалық емес токты тұрақты ток пен әр түрлі бастапқы фазаларынан тұратын синусоидалық токтардың жалпы қосындысы деп алсақ болады. Бұндай тұжырымдаманы периодты синусоидалық емес токтарды есептегенде жиі қолданылады.
1. 2 Синусоидалық емес кернеу
4. 1 - суретте тек бірінші
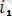
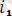 және екінші
және екінші
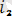
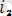 гармоникадан тұратын периодты синусоидалық емес тоқтың графигі көрсетілген. Бұл суретте (4. 1) тізбектің кез келген бөлігінде кернеу:
гармоникадан тұратын периодты синусоидалық емес тоқтың графигі көрсетілген. Бұл суретте (4. 1) тізбектің кез келген бөлігінде кернеу:
u=
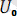
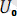 +
+
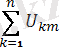
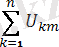 sin(kwt+
sin(kwt+
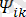
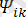 ),
),
ал ЭҚК
e=
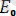
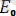 +
+
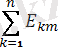
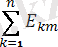 sin(kwt+
sin(kwt+
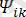
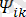 ) - тең.
) - тең.
Ал сызықты тізбек үшін периодты синусоидалық емес тоқты (r, L, C элементтері ток пен кернеуге тәуелді болмайтын тізбек) беттестіру әдісін қолданамыз. Гармоникалық құраушылар мен тұрақты құраушыларды (егер болса) әр қайсысын жеке анықтаймыз ( тәуелсіз турде) .
1. 3 синусоидалық емес тоқтың ЭҚК
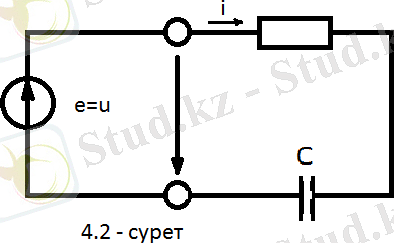
Осыған орай жай қарапайым мысал келтірейік, резисторлы элементтері бар кедергіден r және электр сыйымдылығынан тұратын 4. 2 - суреттегі схеманы қарастырайық. Берілген кернеудегі оның периодты синусоидалық емес тоқтың ЭКҚ:
u=e=
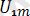
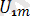 sin(wt) +
sin(wt) +
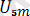
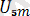 sin(5wt+
sin(5wt+
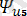
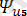 ) .
) .
Бұл тізбекте ток:
i=
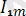
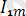 sin(wt-
sin(wt-
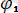
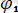 ) +
) +
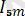
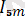 sin(5wt
sin(5wt
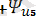
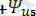 -
-
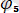
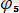 ),
),
осыдан Ом заңы бойынша бірінші гармоника үшін
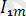
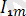 =
=
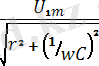
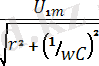 ,
,
Бесінші гармоника үшін
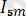
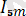 =
=
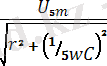
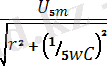 ,
,
Бұл жағдайда фазаларында есептесек
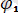
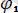 =arctg(-1/wCr) ;
=arctg(-1/wCr) ;
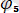
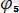 =arctg(-1/5wCr) .
=arctg(-1/5wCr) .
Арине, күрделі тізбек үшін гармоникалық құраушыларды анықтау үшін тізбектің синусоидалық тоқты анықтайтын кез келген әдісті (комплексті әдісті қоса) қолданса болады.
2. 1 Периодты синусоидалық емес тоқтың пайдалы мәні.
Жалпы токтың мәнін және басқада өлшемдерді жоғарыда атап өткендей беттестіру әдісімен есептесе болады. Бірақта, практика жүзінде токтың пайдалы мәндерін (кернеу, ЭКҚ) амперметр (вольтметр) есептеу маңызы зор.
Келтірілген кез келген периодты токтың мәнін тұрақты токтың жылулық қозғалысты ескере отырып, периодты синусоидалық токтың мәнін былайша есептейміз:
I=
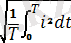
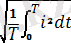 . (4. 3)
. (4. 3)
4. 1 - суреттегі интегралды ескерсек
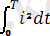
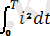 =
=
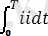
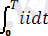
Төрт типті интеграл мәнін анықтайық
- ==,
Бұл интегралдың анықталуы бойынша квадраттанған
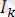
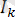 мәніндегі k-сыншы реттік гармоникалық құраушыға тең. Осыдан:
мәніндегі k-сыншы реттік гармоникалық құраушыға тең. Осыдан:
- =- құраушы тұрақты токтың квадраты;
- ==0,
Осыдан:
Мұнда k, l - гармоникалардың номерлері, және де k
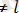
 ; синусоидалды функцияның көбейтінділерін косинусоидалылардың әр түрлілігіне ауыстыруға болатындықтан, интеграл нөлге тең:
; синусоидалды функцияның көбейтінділерін косинусоидалылардың әр түрлілігіне ауыстыруға болатындықтан, интеграл нөлге тең:
sinβ

 sinγ=
sinγ=
 ,
,
яғни, интегралдардан 4-ші типі екі косинусоидалдың әр түрлігі болып келеді, әр бүтін сан үшін интеграл период саны нөлге тең.
Осыдан қорыта отырып, периодты синусоидалық емес токтың мәні:
I=
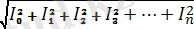
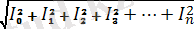 ,
,
Немесе
I=
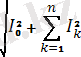
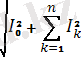 , (4. 4)
, (4. 4)
Яғни, периодты синусотдалдық емес пайдалы токтың мәні түбір астындағы тұрақты және гармоникалық құраушыларының квадраттарының қосндысындыларына тең. Осылайша периодты синусоидалық емес пайдалы кернеудің мәнін есепке алсақ болады:
U=
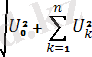
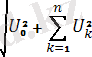 (4. 5)
(4. 5)
Осыған ұқсас периодты синусоидалық еместің басқада өлшемдерін.
2. 2 Периодты синусоидалық емес токтың қуаты.
Жалпы кедергіні есептеу үшін
p=iu (4. 6)
Кез келген периодты ток үшін активті қуаты жартылай периодтағы жалпы қауттың мәніне тең:
P=
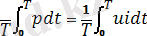
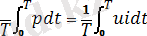 . (4. 7)
. (4. 7)
қуаттың (4. 6), кернеудің (4. 2) және де токтың (4. 1) анықталғанан кейін периодты синусоидалдық емес токтың активті қуаттың қатары төрт түрлі типті интегралдарға юөлсек болады:
- , мұнда;
- ;
- ;
;
- ; ( kl ескере)
Сайып келгенде, активті кедергі:
P=
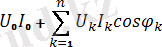
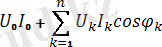 , (4. 8)
, (4. 8)
Яғни, периодты синусоидалдық емес токтың қуаты барлық гармоникалық және тұрақты құраушылардың активті кедергілерінің қосындыларна тең.
Периодты синусоидалдық емес токтардың реактивті қуатының мөлшерін мына формуламен есептесе болады:
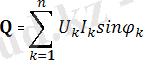
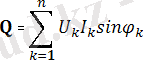 ; (4. 9)
; (4. 9)
Периодты синусоидалдық емес токтың толық қуаты анықталады:
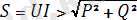
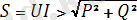 ; (4. 10)
; (4. 10)
2. 3 Электірлі фильтрлер.
Тізбектегі периодты синусоидалдық емес токтың әр түрлі гармоникалық құраушылары осы токтағы катушканың индуктивті кедергілері kwL және кондесатордың сыйымдылық кедергілері 1/kwC бірдей емес, себебі гармоникалық құраушының рет номеріне k тікелей байланысты. Сондықтанда қисықтардың формасындағы кернеу мен токтың жалпы мәнін және токтардың лайықты таңдалған тізбектегі элементтерінің параметрлерін өзгертсе болады.
Тізбектегі токтың элементтерінің параметрлерінің кисықты формаға әсер етуін түсіну үшін екі қарапайым мысал келтірейік.
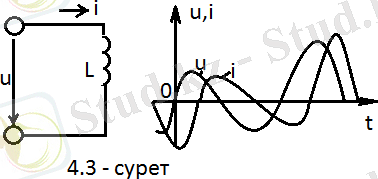
Периодты синусоидалық емес токтың кернеуі индуктивті элементке қосымша тіркелген (4. 3 - суретте), жәнеде ол мына мәнге ие:
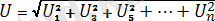
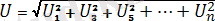 . (4. 11)
. (4. 11)
Ом заңы бойынша k-шы гармоникалық ток
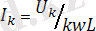
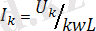 .
.
Демек, жұмыс істейтін токтың мәні (4. 4) -дан
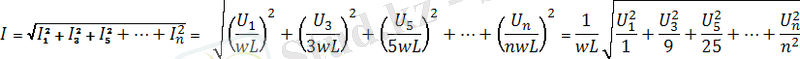
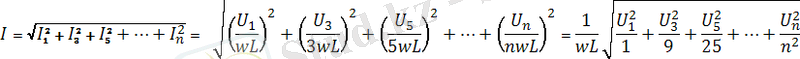 .
.
Осы жоғарыдағы токтың мәнін кернеудің (4. 11) мәнімен салыстырсақ, индуктивтік элементте периодты синусоидалдық емес токтың жоғарғы гармоникалық құраушыларының мәні гармоникалық құраушының реттік номері артқан сайын басым болады. Сол себептен, қисықтың кернеуінен қарағанда, осы қисық токтың мәні синусоидалық токтың мәнінен айырмашылығы аз болады (4. 3 - суретте) .
Сыйымдылықтың элементі үшін (4. 4 - суретте) кернеудің осы мәнімен (4. 11) k-сыншы гармоникалық токтың мәнін салыстырамыз:
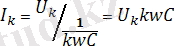
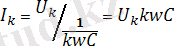 .
.
Демек, жумыс істейтің токтың мәні (4. 4) -ден
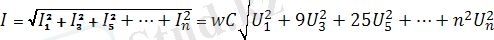
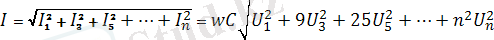 . (4. 12)
. (4. 12)
(4. 12) мен (4. 11) -ының мәндерін салыстыра отырып, қисық токқа қатысты жоғарғы гармоникалық құраушылары қисық кернеудегінен көп болуы мүмкін екендігін көреміз. Сол себепті, осы қисық ток қисық кернеуден қарағанда синусоидты токтан айырмашылықтары көбірек (4. 4 - суретте) .
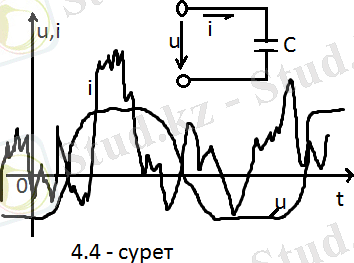
Егер сыйымдылық пен индуктивтіліктің элемент параметрлерін өлшеген кезде синусоидалық емес ток пен кернеуді есерке алмасақ, бұл үлкен қателікке алып соғады. Ұұсыныс жасайық, кондесатор сыйымдылығын өлшеу кезінде оның аралық периоды периодты синусоидалық деп, яғни жумыс істейтің кернеу мәні (4. 11) -ден берілсін. Кернеу мен ток синусоидалық деп есептесек, кондесатордың сыйымдылығын мыналар арқылы табамыз:

 ;
;
Осыдан
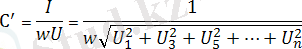
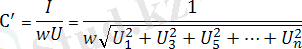 ;
;
Содан (4. 12) -мен байланыстырсақ:
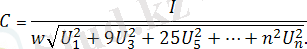
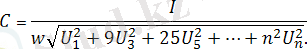 .
.
C’ мен С сыйымдылықтарды салыстырсақ, біріншісі улкен болады. Осыған ұқсас индуктивтіліктіде салыстырсақ болады ; )
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz