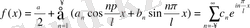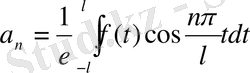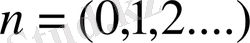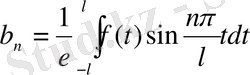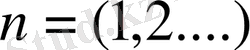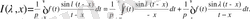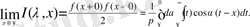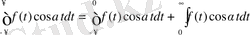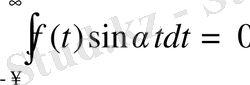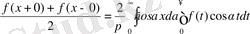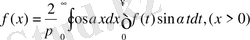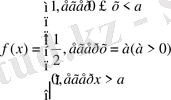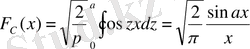Жалпы білім беру курсында Фурье интегралы мен Фурье қатарларының оқыту әдістемесін жетілдіру


Мазмұны
Кіріспе . . . 3
Негізгі бөлім . . . 5
1. Фурье интегралы . . . 5
1. 1 Фурье түрлендіруі . . . 9
1. 2 Фурье интегралының комплекс түрі . . . 13
1. 3 Функцияны Фурье интегралымен жазып көрсету . . . 14
2. Фурье қатарының шектік жағдайы . . . 15
2. 1 Фурье формуласының әр қилы түрлері . . . 19
2. 2 Периоды 2π функцияның Фурье қатары . . . 21
2. 3. Жұп және тақ функциялардың Фурье қатары . . . 25
Қорытынды . . . 27
Пайдаланылған әдебиеттер . . . 28
Кіріспе
Қазақстан Республикасының білім беруді жетілдірудің басты міндеті - білім берудің қазіргі заманғы сапасын қамтамасыз ету және білім беру жүйесінің барлық мемекеттің өзекті әрі болашақ сұранысына сәйкестікке келтіру болып табылады.
Қазіргі таңда фундаментальді ғылыми пәндер бойынша бағыттағы білікті мамандар дайындауды соның ішінде математикалық білім деңгейінің жоғары болуына аса көңіл бөлініп отыр.
Табиғаттану ғылымдарымен техникада математика баяндалуы периодты функциялармен өрнектелетін алуан түрлі тербеліс процесімен кездестіруге тура келеді. Фурье қатарларымен олардың екінші бір көрінісі - Фурье интегралы осындай құбылыстарды зерттеудің қуатты аппараты болып табылады.
Фурье қатарлары теориясының математиканың қолданылуында айта қалғандай маңыздылығы ескеріліп, ол жоғары математика курсының фундаменттік негіздерінің бірі ретінде жобада баяндалады.
Фурье, Эйлер сияқты, мүшелеп интегралдауды қолданып функцияның тригонометриялық жіктеу коэффициенттері үшін интегралдық формулалар тағайындайды. Осы формулалар бойынша «кез-келген функциялар» үшін коэффициенттерді есептеудің оңай екендігіне қарап, оның осындай барлық функциялар үшін жіктеудің мүмкін болатындығына көзі жетті. Фурье замандастарына аралықтың әр түрлі бөліктерінде әр түрлі заңға бағынатын функциялардың жіктелуі қатары әсер етті.
Бірқатар жағдайларда Фурье құрған жіктеулердің сәйкес функцияларға жинақталатынын тікелей тексеру мүмкін болды. Екінші жағынан, бұл жіктеулер математикалық физикада кеңінен қолданылатын болды. Солай бола тұрса да, Фурье идеяларын бастапқы кезде көпшілік мақұлдай қоймайды: мүшелеп интегралдау ол тұста әдетте бір болатын, алайда ол жіктеу мүмкіндігін дәлелдемейді, тек білдереді міне, әңгіме енді осы мүмкіндікті дәлелдеуге келіп тіреліп қалды.
Шынын айтқанда, Фурье өз шығармасының аяқ жағында функцияның тригонометриялық жіктелуі дұрыстығын дәлелдемек болып әрекет жасайды, алайда оның келтірген талқылаулары аналитикалық дәлдігі жағынан мүлтіксіз емес еді, бірақ оның геометриялық формаға келтірген негізгі идеясы дұрыс болатынды. Бұдан кейін басқа авторлар да, соның ішінде Коши де, талаптанып көрді, бірақ бұларға қарсы пікір айтушылар да табылды.
Фурье айтқан ұйғарымның бірінші болып шын мәніндегі мүлтіксіз дәлелдемесін келтірген Дирихле еді.
Функцияның тригонометриялық жіктеуінің бірден-бірлігі жөніндегі мәселе туды: өйткені осындай жіктеудің коэффициенттерін беретін Эйлер-Фурье формулалары қатарды мүшелеп интегралдау жолымен табылды, ал өткен ғасырдың екінші жартысында бұл сияқты тәсізді сөзссіз қолдану мүмкін еместігі жете түсінілді.
f(x) функциясының бірден-бір жіктеуінің коэффициенттері қандай болмақ? Олар қашан да сол Фурье коэффициенттері болмақ па? Әрине бұл сұрақты Эйлер-Фурье формулаларындағы интегралдардың жалпы мағынасы болатын функциялар жөнінде қойған дұрыс болар еді. Бір тамашасы, ол сұраққа мақұлдап жауап беруге болады екен, бұны алдымен 1872ж үздіксіз функциялар үшін Асколи ал меншікті мағынасында интегралданатын функциялар үшін дю Буа-Реймон тағайындады. Бертін келе бұл нәтиже анағұрлым жалпылау мағынада интегралданатын функцияларға да қолданылатын болды. Зерттеушілердің функцияларды Фурье қатарларына жіктеу мәселесіне соншалықты төтенше назар аударғандығы осы еңбектермен ақталғандай болды.
Енді тағы бір мәселеге тоқтап өтейік. Дирихле периды 2π әрбір үздіксіз функция Фурье қатарына жіктеледі деп нық сенді, алайда мұны ол дәллдей алмады. Біл пікірді, сірә басқа математиктер де қолдаған сияқты. Алайда дю Буа-Реймон Дирихле ұйғарымының дұрыстығын дәлелдемек болып бірқатар әрекеттенгеннен кейін, 1876ж. мысалмен оны теріске шығарды, бұл үшін ол мейілінше кішкене аралықтағы шектеусіз көп нүктелер жиынында Фурье қатары жинақты болмайтын үздіксіз функция құрды.
Курстық жұмыстың мақсаты Жалпы білім беру курсында Фурье интегралы тақырыбын оқыту әдістемесін жетілдіру.
Осы мақсатқа сәйкес курстық жұмысты орындауда мынадай міндеттер қойылды:
- Фурье интегралы
- Фурье түрлендіру
- Фурье қатарының шектік жағдайы
Зерттеу пәні Жалпы білім беру курсында Фурье интегралымен, қатарының шектік жағдайын жалпы түсінікті қалыптастыру.
Курстық жұмыстың құрылымы кіріспеде зерттеу мәселесі, нысаны, зерттеу мақсаты, әдіснамалық негізі теориялық және практикалық маңыздылығы анықталады.
1 Фурье интегралы
1. Егер функция f(x)
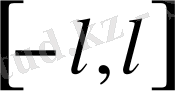 сегментінде берілсе және Фурье қатарының жинақтылық шарттарын қанағаттандыратын болса, онда
сегментінде берілсе және Фурье қатарының жинақтылық шарттарын қанағаттандыратын болса, онда
немесе
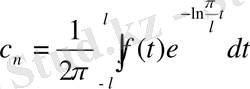
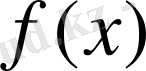 функцияны периодты етіп жалғастырмай-ақ,
функцияны периодты етіп жалғастырмай-ақ,
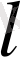 -ді шексіздікке ұмтылып
-ді шексіздікке ұмтылып
 айнымалы х-тің барлық нақты мәндерінде анықталған периодсыз функция үшін аналитикалық өрнекті қалай табу керек?
айнымалы х-тің барлық нақты мәндерінде анықталған периодсыз функция үшін аналитикалық өрнекті қалай табу керек?
Берілген
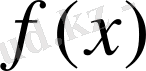 функцияның әрбір шектеулі аралықта абсалют интегралданатын туындысы болсын және (-∞, ∞) аралықта бұл функцияның өзі абсалют интегалданатын болсын, яғни
функцияның әрбір шектеулі аралықта абсалют интегралданатын туындысы болсын және (-∞, ∞) аралықта бұл функцияның өзі абсалют интегалданатын болсын, яғни
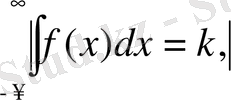
мұнда к- тұрақты сан.
Егер х - үзіліс нүктелерін сипаттайтын болса, онда бұл нүктелердегі функцяның мәндерін былай анықтаймыз:
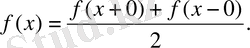
Жоғарыда қойылған сұраққа келесі теорема жауап болып табылады.
Теорема
Егер
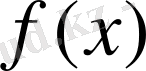 функцияның әрбі шектеулі аралықта абсалют интегралданатын туындысы болса және (-∞, +∞) аралықта бұл функцияның өзі абсалют интегралданатын болса, онда айнымалы х-тің барлық мәндері үшін төмендегі теңдік
функцияның әрбі шектеулі аралықта абсалют интегралданатын туындысы болса және (-∞, +∞) аралықта бұл функцияның өзі абсалют интегралданатын болса, онда айнымалы х-тің барлық мәндері үшін төмендегі теңдік
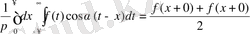 (1)
(1)
орындалады.
Осы тұжырымдалған теореманы Фурье теоремасы деп, ал (1) теңдіктің сол жағындағы интегралды Фурье интегралы деп атайды.
(1) формуланың дұрыстығын дәлелдеу үшін, келесі теңдіктің
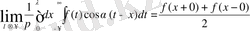
дұрыстығын дәлелдеу керек.
Кейінгі теңдіктің сол жағындағы интегралды
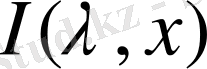 арқылы белгілеп, интегралдау ретін ауыстырайық.
арқылы белгілеп, интегралдау ретін ауыстырайық.
(2)
функция
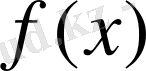 абсалют интегралданатын болғандықтан мына меншіксіз интеграл
абсалют интегралданатын болғандықтан мына меншіксіз интеграл
(3)
α-ның барлық мәндерінде де бірқалыпты жинақты болады. Сондықтан (3) интегралды параметр α бойынша интеграл таңбасы ішінде интегарлдауға болады. Ендеше (2) формула дұрыс, яғни
.
Енді осы кейінгі теңдіктің оң жағындағы қайталама интегралдың ішкі интегралын α бойынша интегралдап табамыз:
Бұл теңдіктің оң жағында тұрған бірінші интегралдағы (t-x) -тың орнынан - z-ті, екінші интегралдағы (t-x) -тың орнынан z-ті қойып табамыз:
(4)
Енді біз мына теңдіктердің
(5)
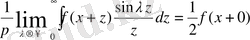
дұрыстығын дәлелдейік.
 - алдын-ала берілген оң құнарсыз аз сан болсын. Егер z>1 болса, онда λ қандай болса да
- алдын-ала берілген оң құнарсыз аз сан болсын. Егер z>1 болса, онда λ қандай болса да
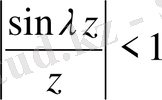 болады, ал фунция f(x-z) теореманың шарты бойынша
болады, ал фунция f(x-z) теореманың шарты бойынша
 аралықта абсалют интегралданатын болғандықтан, бірден артық соншама үлкен N cаны (N>1) табылып, λ қандай болса да келесі теңсіздік орындалады:
аралықта абсалют интегралданатын болғандықтан, бірден артық соншама үлкен N cаны (N>1) табылып, λ қандай болса да келесі теңсіздік орындалады:
(6)
Енді төмендегі теңдікті
(7)
пайдаланамыз. Екінші жағынан
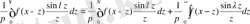 (7)
(7)
Енді λ-ны шексіздікке ұмтылтып, (7) теңдіктің екі жағынан шек алайық. Сонда
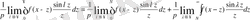
(5) және (6) қатыстарды еске алып табамыз:
(8)
Дәл осы сияқты
(9)
(4) теңдіктің екі жағынан шек алып табамыз:
сонымен теорема дәлелденді.
2 Функция f (x) жұп болсын. Сонда
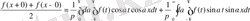
ішкі интегралды жеке алайық:
Бұл теңдіктің оң жағында тұрған бірінші интегралдағы t-нің орнына - t-ні алсақ, онда
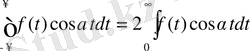
Ал
Сонымен, жұп функция үшін
Егер f(x) - тақ болса, онда
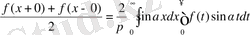
Егер функция f(x) тек (0, ∞) аралықта ғана анықталса, онда оны тетелес (көршілес) жатқан (-∞, 0) интервалда жұп не тақ түрде жалғастырамыз. Сонда,
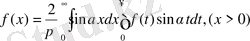
1. 1 Фурье түрлендіруі
Біздің ұйғарым жасағанда Фурье формуласы (10) х-тің барлық мәндері үшін (-∞, +∞) аралықта дұрыс болады. Бұл формуланы мынадай екі формуланың суперпозиициясы ретінде көрсетуге болады:
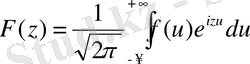
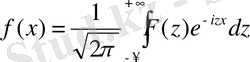 (13)
(13)
f(x) функциясының бірінші формуласы бойынша салыстырылатын F(z) функциясы оның Фурье түрлендіруі деп аталады. Ал екінші формула бойынша F(z) функциясы функциясы үшін f(x) функциясы (кері) Фурье түрлендіруі болып табылады (айырмашылығы тек і-дің таңбасында ғана) . F функциясы, жалпы айтқанда f заттық болғанның өзінде комплекс функция екендігін ескертеміз. Алайда мұнда бастапқы f функциясын комплекс функция деп те алуға болатын еді.
Мына теңдікті
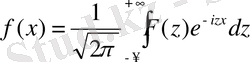
(f(x) функциясы берілген) интеграл астындағы белгісіз F(z) функциясына қатысты интегралдық теңдеу ретінде қарастыруға болады. Теңдеудің шешуі мына формуламен орындалады:
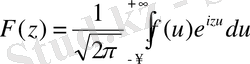
бұл теңдіктердің рольдерін алмастыруға болатыны түсінікті.
Енді (11) формулаға қайта оралайық. Ол х-тің барлық оң мәндері үшін орындалады және оны бұл жолы нақты және де нағыз симметриялы екі формуланың суперпозициясы ретінде көрсетуге болады
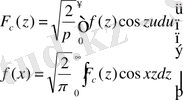 (14)
(14)
Тап осылайша (12) формула да екі формулаға ажыратылады:
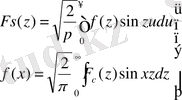 (15)
(15)
F c (z) және F s (z) функциялары сәйкес түрінде Фурьенің f(x) функциясы үшін Фурьенің косинус- түрлендірулері немесе синус- түрлендірулері деп аталады. Көріп отырғанымыздай f функциясы F c (не F s ) бойынша нақ F c (не F s ) функциясы f бойынша F c ( F s ) сияқты шығады. Басқаша айтқанда, f және F c ( F s ) функциялары өзара косинус (синус) түрлендірулер болмақ. Коши f пен F c не f пен F s функцияларды қосарлап сәйкес түрде бірінші және екінші текті түйіндес функциялар деп атаған. Бұл жерде де (14) (не (15) ) теңдіктердің әрқайсысын (интегралдан тыс функция берілген де, ал интеграл астындағысы ізделінеді) интегралдық теңдеу ретінде қастыруға болады. Шешуі басқа теңдікпен беріледі.
F, F c , F s функцияларын салыстырып былай деуге болады. f(x) функциясы жұп болған жағдайда шығатыны
F(z) =F c (z)
(z<0) мәндерінде F c (z) функциясы жұп түрінде таралады. Ал f(x) функциясы тақ болған жағдайда
F(z) =іF s (z)
(z<0) мәндерінде F s (z) функциясы nf0 түрінде таралады. Жалпы алғанда f(x) функциясы жұп және тақ функциялардың қосындысына ажырайды:
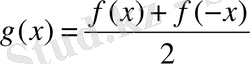
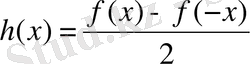
Сонда
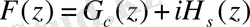
Осы жағдаймен байланысты косинус-синус түрлендірулерімен қанағаттану жеткілікті.
1) Айталық
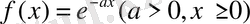 болсын, сонда оның косинус-түрлендіруі мына функция болмақ
болсын, сонда оның косинус-түрлендіруі мына функция болмақ
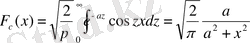
ал синус-түрлендіруі - мына функция
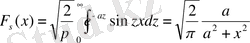
e -ax функциясы [0, ∞] аралықта интегралданатын болғандықтан, мына өзара қатынастар да дұрыс болуы тиіс:
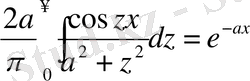
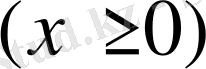
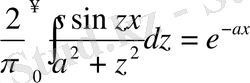
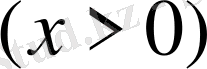
немесе
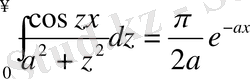 ,
,
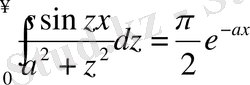
Біз бұл интегралдардың Лаплас интегралдары екендігін көреміз.
[n 0 308, 4 0 ]
Сонымен, мына қос функция
е
-ах
,
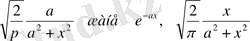
бірінші және екінші текті (Коши бойынша) түйіндес функциялардың мысалдары болмақ. Егер бізге Лаплас интегралдары белгілі болмаса, онда баяндалып отырған теорема оларды есептеп шығаруға жол нұсқар еді.
- Енді мына теңдіктермен анықталатын функцияны қарастырайық:
Бұл жағдайда
Осы мысал арқылы да Фурье формуласын тексеріп көру мақсатымен табылған функция үшін косинус-түрлендіруді табамыз:
Егер бұл интегралды мына түрде қайта жазсақ:
онда, шынында да, оның бастапқы f(x) функциясымен дәл келетіні анық болады.
3) Фурьенің
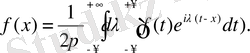 түріндегі интегралын өзгертіп былай жазуға болатыны анық:
түріндегі интегралын өзгертіп былай жазуға болатыны анық:
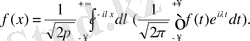
Сонда формула
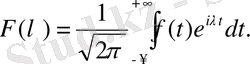
f(x) функциясы үшін Фурьенің тура түрлендірмесі деп аталады. Демек, бұл формула мына түрге келеді:
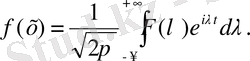
Бұл формула F(
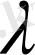 ) функциясы Фурьенің кері түрлендірмесі деп аталады.
) функциясы Фурьенің кері түрлендірмесі деп аталады.
1. 2 Фурье интегралының комплекс түрі
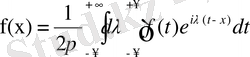
Шынында бұл формуладағы
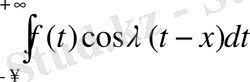 өрнегін параметр
өрнегін параметр
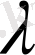 -ның (-∞, +∞) аралығында анықталған жұп функциясы, ал
-ның (-∞, +∞) аралығында анықталған жұп функциясы, ал
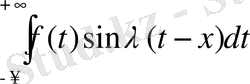 - тақ функция деп қарастырсақ,
- тақ функция деп қарастырсақ,
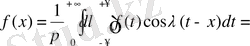
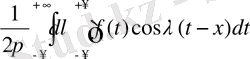 (1)
(1)
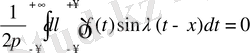 (2)
(2)
болар еді.
- (2) - ны біріктіріп, әрі
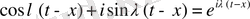
екенін ескерсек, онда интегралды формуланың комплекс түріндегі жазылысын аламыз.
1. 3 Функцияны Фурье интегралымен жазып көрсету
n 0 402 теоремаға толық ұқсас болатын мына теорема да дұрыс.
Теорема f(x) функциясы әрбір шектеулі аралықта үзінді-дифференциалданатын болсын және де [-∞, +∞] аралық абсалют интегралданатын болсын. Сонда әрбір х=х 0 нүктеде оның Фурье интегралы жинақталады және мәні
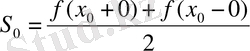
болады (егер функция х=х 0 нүктесінде үздіксіз болса, оның f(x 0 ) -ге тең болатыны түсінікті) .
Дәлелдеме Теңдіктің екі жақ бөлігін де
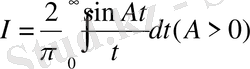
[n 0 293, ескерту n 0 308, 2 0 ] тұрақты S 0 санына көбейтіп, нәтижені (5) теңдіктен мүшелеп шегереміз: сонда:
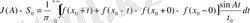 (6)
(6)
Тұрақты h>0 санын алып, бұл интегралды мына түрде көшіріп жазамыз:
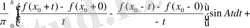
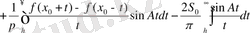
Бірінші интегралдың А→∞ жағдайда нольге ұмтылғандағы n 0 402 теореманы дәлелдегендей тағайындалады. Екінші интегралдағы бөлшек өрнек, f-пен қоса, [h, ∞] аралықтың кез келген шектеулі бөлігінде үзінді-үздіксіз функция болмақ; оның үстіне бұл функция аталған аралықта абсалют интегралданады. Олай болса, алдыңғы n 0 -тың аяғында келтірілген ескерту бойынша екігші интегралдың да А→∞ жағдайдағы шегі нольге тең болады. Ақтығында, соңғы интегралда Аt=z деп алып, оны мына түрге келтіреміз:
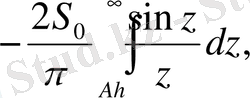
Ендеше бұл да А→∞ жағдайда нольге ұмтылады. Бұдан жасайтын қорытындымыз: (6) өрнектің А→∞ жағдайындағы шегі ноль болады, яғни (2) интеграл болады және S 0 -ге тең.
2. Фурье қатарының шектік жағдайы
Егер f(x) функциясы шектеулі [-l, l] аралықта берілген болса, онда белгілі бір шарттар орындалғанда оны осы аралықта тригонометриялық қатар арқылы жазып көрсетуге болады:
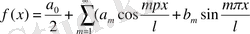 ,
,
мұнда
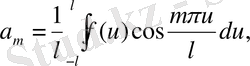
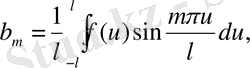
(m=0, 1, 2, …) (m=1, 2, …)
a m және b m коэффициенттерінің орнына олардың өрнектерін қойып, қатарды мына түрде қайта жазуға болады:
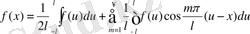 (1)
(1)
Енді f(x) функциясы бүкіл шектеусіз (-∞, +∞) аралықта анықталған болсын, бұл жағдайда, х қандай болса да, сәйкес f(x) мәні кез келген [x] <l мәнінде (1) жіктеумен өрнектеледі. Бұл жерде l→+∞ жағдайда шекке көшіп, осы жіктеудің «шектік формасын» тағайындап көреміз.
(1) теңдіктің оң жақ бөлігіндегі бірінші мүшесін нольге ұмтылады деу орынды. Шектеусіз қатар болған жағдайда косинус таңбасының астындағы
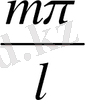
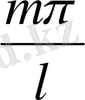 көбейткіштерді қандай да бір z айнымалының z
0
=0-ден +∞ дейін ылғи өзгеріп отыратын
көбейткіштерді қандай да бір z айнымалының z
0
=0-ден +∞ дейін ылғи өзгеріп отыратын
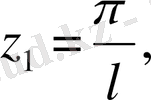
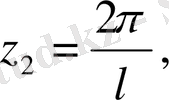 . . . ,
. . . ,
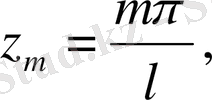 . . .
. . .
дискретті мәндері деп қарастырыуымызға болады; сонда өсімше
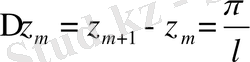
l→+∞ жағдайда нольге ұмтылатыны айқын. Мұндай белгілеулерден кейін біздің қатарымыз былай жазылады:
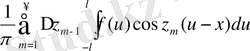
Ол мына z-тің функциясы үшін
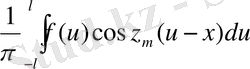 [0, +∞] аралықтағы интегралдық қосындыны білдіреді. l→+∞ жағдайда шекке көшіп, қатардың орнына интеграл шығарып аламыз; тап осындай жолмен Фурьенің интегралдық формуласына келеміз:
[0, +∞] аралықтағы интегралдық қосындыны білдіреді. l→+∞ жағдайда шекке көшіп, қатардың орнына интеграл шығарып аламыз; тап осындай жолмен Фурьенің интегралдық формуласына келеміз:
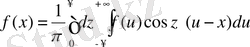
Айырманың косинусы өрнегін жайып жазып, бұл формуланы мына түрге қайта жазуға болады:
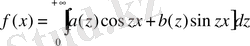
мұнда
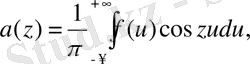
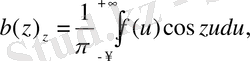
Бұл жерде тригонометриялық жіктеумен ұқсастықтың бар екендігі анық байқалады: тек натурал қатар мәндеріне ие болатын параметр m ғана ылғи өзгеріп отыратын параметр z-пен, ал шектеусіз қатар интегралымен алмастырылған a(z) және b(z) коэффициенттері де өзінің құрылысы жағынан Фурье коэффициенттеріне ұқсас.
Әрине, осы айтылғандардың барлығы салыстырудан шығып отыр. Фурье формуласы дұрыс болу үшін қолайлы нақты шарттарды әлі анықтау қажет болады. Алайда, тәпіштеп талқылайтын болғанда Фурье қатарымен байланысты талқылаулардың басты кезеңдерін қалдырмай орындайтын боламыз.
Ескертулер f(x) функциясын енді ол 1) әрбір шектеулі аралықта үзінді-үздіксіз және 2) шектеусіз [-∞, +∞] аралықта абсалют интегралданады деп аламыз. Осылай ұйғарып алып, мына интегралды қарастырамыз:
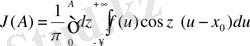
мұнда А- кез келген шектеулі оң сан, ал х 0 дегеніміз х-тің кез келген белгіленген мәні. Бұл интеграл Фурье қатарының дербес қосындысына ұқсас: одан Фурье интегралы
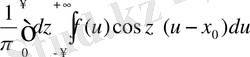 (2)
(2)
A→+∞ жағдайдағы шегінде шығады.
Кез келген шектеулі В>0 болғанда, 4- теорема бойынша [n 0 298] шығатыны
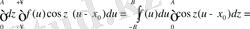
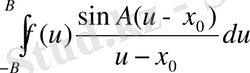 (3)
(3)
Егер f(u) функциясы [-B, B] аралықта үздіксіз болса, айтылған теоремадан бұл тікелей шығады; кері жағдайда теореманы функция үздіксіз болатын аралықтардың әрбіреуіне жеке-жеке қолдануға тура келер еді.
Алайда интеграл
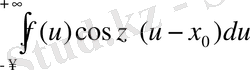 (4)
(4)
Ұйғару бойынша жинақталатын
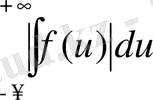
интегралымен мажоранттанады, олай болса z-ке қатысты алғанда оның мәндерінің кез келген аралығы үшін (u=+∞ және u=-∞ болғанда да) бір қалыпты жинақталады. Сонымен, интеграл
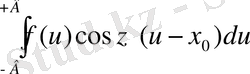
В→+∞ жағдайда өзінің (4) шегіне бір қалыпты ұмтылады. Сондықтан, (3) теңдікте В→+∞ жағдайда шекке көше отырып, интегралдың сол жағында шектік көшуді интеграл таңбасының астында орындауға болады. Бұдан I(A) үшін интеграл
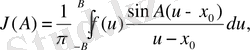
Бұл Дирихле интегралына ұқсас [n 0 399] және шынында да, тап сондай рольді атқарады. Оңай түрлендіру жасап, оны мына түрге келтіруге оңай:
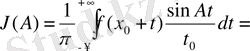
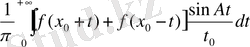 (5)
(5)
Баяндау жолын әрі қарай жалғастыра түсу үшін n 0 400-тегі негізгі лемманы былайша толықтыру керек болады.
g(x) функцияcы [а, +∞] аралықтың әрбір шектеулі бөлігінде үзінді-үздіксіз болып және осы шектеусіз аралықта абсалют интегралданатын болса, онда
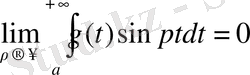
болады, тап солай
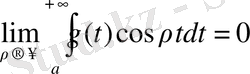
Шынында да, кез келген сан
 алып,
алып,
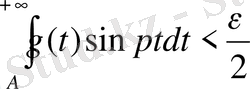
орындалатындай етіп біз алдымен А-ны соншалықты үлкен етіп аламыз, сонда сөзсіз
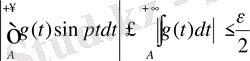 орындалады және p-нің мәніне тәуелді болмайды. Ал бұдан кейін мына интегралға
орындалады және p-нің мәніне тәуелді болмайды. Ал бұдан кейін мына интегралға
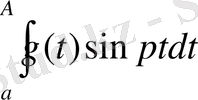
n 0 400 лемманы тікелей қолданамыз сонда жеткілікті үлкен p-лер үшін
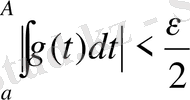
болады, р-нің сол мәндері үшін
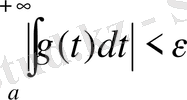
орындалатыны айқын, дәлелдемекшіміз де осы болатын.
2. 1 Фурье формуласының әр қилы түрлері
Фурье формуласының жоғарыда көрсетіп өтілген қолданылу шарттары орындалады деп ұйғарып, оңай болу үшін қарастырылып отырған х нүктесінде f(x) функциясы үздіксіз немесе егер үзілісті болса онда мына шартты:
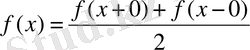
қанағаттандырады деп есептейміз. Сонда қалай да мынау шығады:
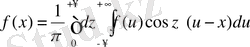
Ішкі интеграл z-тің жұп функциясы болып табылатын себепті, бұл формуланы былай көшіріп жазуға да болады:
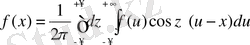 (8)
(8)
Енді n 0 410-та f(x) функциясы жөнінде жасалған жалпы ұйғарымдардан кейін мына интегралдың да
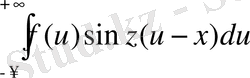 (9)
(9)
болатынын көрсеу оңай. Бұл интеграл, мұнымен бірге z-тің үздіксіз функциясы да, әрі тақ.
Жалпы алғанда, бұл функция үшін -∞-тен +∞-ке дейінгі меншікті емес интеграл болады деп кесіп айтуға болмайды.
Қандай да ψ(х) функциясы үшін -∞-тен +∞-ке дейінгі интеграл болмайтын жағдайда, мына шек
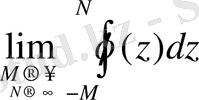
M мен N тәуелсіз түрде шексіздікке ұмтылғанда болмаса, дербес M=N ұйғарымға сәйкес шектің бар болып шығуы мүмкін. Мұндай шекті Кошиге еліктеп, интегралдың бас мәні деп атайды және V. p. (Valeur principale) әріптерімен белгілейді.
V. p.
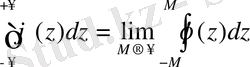
Егер интеграл меншікті емес интегралдың кәдімгі анықтамасына сәйкес түрде бар болса, онда ол оның бас мәнімен бірдей болатыны түсінікті.
z-тің (9) функциясы тақ болатын себепті,
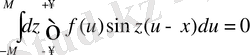
және М→∞ жағдайда шекте бұл жолы да ноль шығады. Сонымен, қалай да
V. p.
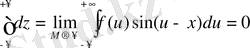
Осы теңдікті
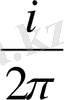 -ге көбейтіп және (8) бен қосып, мына қатысты табамыз:
-ге көбейтіп және (8) бен қосып, мына қатысты табамыз:
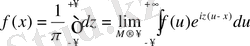 (10)
(10)
мұндағы сыртқы интеграл бас мән деп түсініледі. Формуланы бұл түрде алғаш рет жазып көрсеткен Коши еді.
(7) формулаға қайта оралып, оны мына түрде жазамыз:
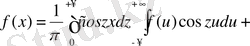
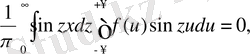
Енді біз тек косинустар ғана енетін ықшам формуланы шығарып аламыз:
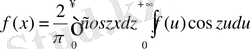 (11)
(11)
Осыған ұқсас f(x) функциясы тақ болғанда тек синустар ғана енетін формулға келеміз:
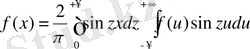 (12)
(12)
Енді f(x) функциясы тек [0, +∞] аралықта ғана берілген болсын және осы аралықта бүкіл (-∞, +∞) аралық тұсында бұрын қойылғандарға ұқсас шарттылықтарды қанағаттанырады делік. Сонда f(x) функциясын
f(-x) =f(x) немесе f(-x) =-f(x) теңдіктер көмегімен (-∞, 0) аралықта таратып (x>0), біз (-∞, +∞) бірінші жағдайда жұп функция, екінші жағдайда тақ функция шығарып аламыз.
Егер х=0 нүктесінде f(x) функциясын үздіксіз деп алатын болсақ, онда (11) формула бұл нүктеге де қолданылады, өйткені жұп түрінде алынған функция бұл жерде өзінің үздіксіздігін сақтап қалады. Ал (12) формула х=0 нүктесіне жалпы қолданылмайды: ол f(0) мәнін, егер ол тек ноль болғанда ғана көрсете алады.
2. 2 Периоды 2π функцияның Фурье қатары
[-π, π] кесіндісінде анықталған Т = 2π болатын
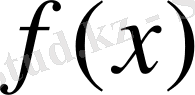 функциясы бір қалыпты жинақталатын тригонометриялық қатарға жіктелсін, яғни:
функциясы бір қалыпты жинақталатын тригонометриялық қатарға жіктелсін, яғни:
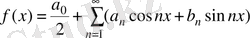 (1)
(1)
болсын. Енді осы қатардың коэффициенттерін табу формуласын қорытайық.
(1) қатар бір қалыпты жинақталады деп жорылғандықтан, оны мүшелеп интегралдауға болады, яғни
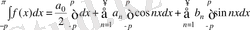 (2)
(2)
Сондай - ақ
 пен
пен
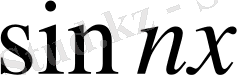 функциялары [-π, π] аралығында ортогональ болғандықтан:
функциялары [-π, π] аралығында ортогональ болғандықтан:
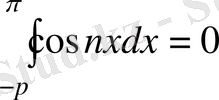 және
және
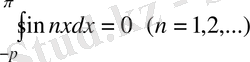 (3)
(3)
Демек, (2) теңдіктен
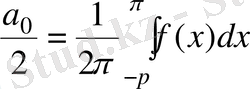 (4)
(4)
болып анықталады. Ал қалған
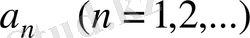 коэффициенттерін анықтау үшін (2) қатардың екі жағын да
коэффициенттерін анықтау үшін (2) қатардың екі жағын да
 өрнегіне көбейту болады, яғни:
өрнегіне көбейту болады, яғни:
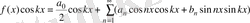 (5)
(5)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz