Евклид және Гильберт кеңістіктері: скаляр көбейтінді, норма, ортогоналдық жүйелер мен базис


Мазмұны
Кіріспе: . . . 3
І тарау. Евклид кеңістігінің элементтері . . . . . . 3
- Скаляр көбейтінді анықталған сызықты кеңістік . . . 4
- Евклид кеңістігінің анықтамасы . . . 5
- Евклид кеңістігінің нормасы . . . 6
- Евклид кеңістігінің мысалдары . . . 8
- Гильберт кеңістігі . . . 10
- Вектордың ұзындығы, екі вектор арасындағы бұрыш . . . 11
- Ортогонал векторлар . . . 12
- Базис . . . 15
- Бессель теңсіздігі . . . 16
- Гильбер кеңістіктерінің изоморфизм19
Қорытынды . . . 23
Пайдаланған әдебиеттер . . . 24
Кіріспе.
Александрия мектебінде ғылым мен өнер, мейлінше құрметтеліп, аса үлкен беделге ие болып тұрды. Математика дамытылып, жаңа сапаға көшеді.
Энгельстің айтуы бойынша: «ғылымның шын мәнінде даралануы алғаш рет осы Александрия мектебінен басталады. О баста философияны, математиканы және жаратылыстануды біріктіретін біртұтас ғылым енді бірнеше дербес ғылымдарға бөлініп, өз алдарына отау тігеді. Бұл ғылымдар ең әуелі астрономия, математика және механика болды.
Александриялық ұлы математиктердің көш бастаушысы, алғашқы қарлығашы Евклид еді. Ол біздің заманымызға дейінгі III ғасырда Александрияға шақырылып, онда математикадан сабақ береді;
Евклидтің өмірі туралы мағлұматтар жоқтың қасы. Ол туралы ел аузында не бары екі аңыз ғана сақталған: «Бірде Птоломей (б. э. дейінгі 300-285 жылдар) патшаның: «геометрияны бейнетсіз, оп-оңай түсінудің жолы бар ма» деген сауалына Евклид: «Геометрияда патшалар үшін айрықша жол жоқ», - деп жауап қайтарыпты. Бірде шәкірті Евклидтен: «геометрияны үйрену нендей пайда береді», - деп сұраса керек, сонда Евклид қызметшіні шақырып алып: «Оқудан пайда тапқысы келіп тұр екен, мына балаға үш теңге беріңіз», - деген екен.
Евклид математика; физика, астрономия, музыка ғылымдары бойынша көптеген еңбектер жазған, Солардың ішінде атақты «Бастамалар», «Берілгендер», «Оптика», «Катоптрика» (айналар теориясы), «Сектио кано-нис» (музыка теориясы), «Фенемондер» (теориялық астрономия) біздерге келіп жетті. Алайда ғылым тарихында Евклид ең әуелі «Негіздер» немесе «Бастамалар» («Начала», грекше «Стихия») деп аталатын классикалық математикалық шығарманың авторы ретінде бағаланады.
Евклидті, бір жағынан, Александрия математикалық мектебінің бастаушысы десек, екінші жағынан, оны ежелгі грек математикасынын соңғы өкілі деп айтуға да болады. Өйткені оның математикадағы жетістіктері өзіне дейінгі грек математикасының 300 жылғы жуық даму нәтижесі, қорытындысы болып табылады.
Евклидтің «Бастамалары» екі мың жылдан аса уақыт дүние жүзі математиктерінің қолынан түспес шығарма болды.
Евклидтің «Бастамалары» 15 кітаптан тұрады. Оның 13 кітабын Евклидтің өзі жазған, қалған екеуі кейінгі грек математиктерінен қосылған. Евклид «Бастамаларының» бірінші кітабын анықтамалар мен аксиомалардан бастайды. Мысалы, бірінші кітаптың басында 23 анықтама, сонан кейін бес постулат және бес аксиома келтіріледі. Сонан соң математикалық сөйлемдер - теоремалар мен салу есептері беріледі. Анықтамалары «Нүкте дегеніміз бөлігі жоқ нәрсе», «сызық дегеніміз еңсіз ұзындық» сияқты өте қысқа да нұсқа келеді.
- Скаляр көбейтiндi анықталған сызықтық кеңiстiк.
Анықтама. Екі вектордың скалярлық көбейтіндісі деп осы векторлардың модульдері мен олардың арасындағы бұрышының косинусының көбейтінділерін айтады:
. (1)
Equation. 3
0 φ
В
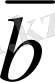
1-мысал.
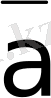 және
және
 векторларының арасындағы бұрыш
векторларының арасындағы бұрыш
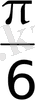 және
және
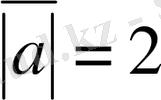 ,
,
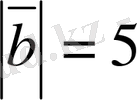 .
.
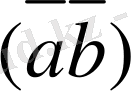 скалярлық көбейтіндісін табыңыз:
скалярлық көбейтіндісін табыңыз:
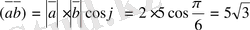 .
.
2-мысал.
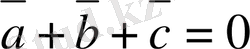 теңдігін қанағаттандыратын
теңдігін қанағаттандыратын
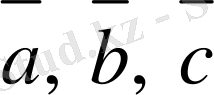 векторлары берілген және
векторлары берілген және
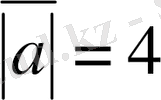 ,
,
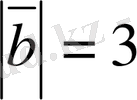 ,
,
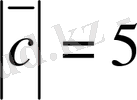 .
.
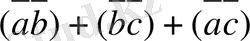 қосындысын табыңдар.
қосындысын табыңдар.
Алдымен
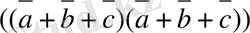 скалярлық көбейтіндісін қарастырайық
скалярлық көбейтіндісін қарастырайық
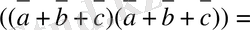
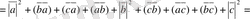
=
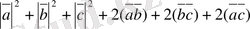 .
.
Есептің шарты бойынша
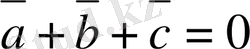 , сондықтан бұл көбейтінді нөлге тең. Ендеше
, сондықтан бұл көбейтінді нөлге тең. Ендеше
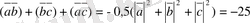 .
.
Кез-келген
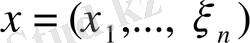 және
және
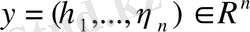 векторлары үшiн олардың скаляр көбейтiндiсi
векторлары үшiн олардың скаляр көбейтiндiсi
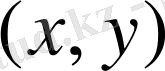 түрiнде таңбаланып, және
түрiнде таңбаланып, және
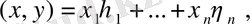 (1. 1)
(1. 1)
теңдігімен анықталады.
Анықтама.
Егер
Е
- сызықтық кеңістiгiнде кез келген
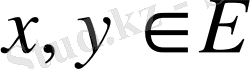 үшін екі айнымалылы, сан мәндi функция
(х, у)
анықталған және ол төмендегі шарттарды қанағаттандыратын болса:
үшін екі айнымалылы, сан мәндi функция
(х, у)
анықталған және ол төмендегі шарттарды қанағаттандыратын болса:
1.
(симметриялық қасиетi) ;
- (аддитивтiк қасиетi) ;
- (комплекс кеңiстiк жағдайында) (біртектiлiк қасиетi) ;
- жәнетек қанаболғанда ғана мүмкiн, ондаЕкеңiстiгiнде скаляр көбейтiндi анықталған деймiз. 1 - 4 шарттары скаляр көбейтіндiнiң аксиомалары деп аталады.
Скаляр көбейтiндi анықталған сызықтық кеңiстiк, әдетте, Евклид кеңiстігi деп аталады. Евклид кеңiстiгiн Е әрпiмен белгiлейік.
Егер анықтама бойынша скаляр көбейтiндiнiң мәндерi нақты (комплекс) сандар болса және векторлар нақты (комплекс) сандарға көбейтілетін болса, онда анықталған Евклид кеңiстiгi нақты (комплекс) кеңiстiк деп аталады. Комплекс кеңiстiк жағдайында симметриялық шарты (х, у) =
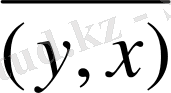 түрiнде жазылады, яғни элементтердiң орындары ауысқанда скаляр көбейтіндiнiң мәні түйіндес комплекс санға өзгередi.
түрiнде жазылады, яғни элементтердiң орындары ауысқанда скаляр көбейтіндiнiң мәні түйіндес комплекс санға өзгередi.
2- және 3- аксиомалар бiрiнші аргументке қатысты болса да, симметриялық аксиоманың салдарынан олар екiншi аргумент үшiн де орындалады. Шынында да,
 (2)
(2)
Осыған ұқсас, 3-аксиомадагы
λ
санын екiншi аргументтің қасынан көбейтiндiнiң алдына шығаруға болатынын, яғни
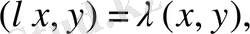 екенiн байқаймыз. Бұл теңдiк комплекс кеңістік жағдайында
екенiн байқаймыз. Бұл теңдiк комплекс кеңістік жағдайында
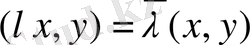 түрiнде болады. Шынында да,
түрiнде болады. Шынында да,
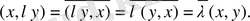 (3)
(3)
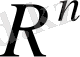 кеңiстiгiнде (1) теңдiгiмен анықталған скаляр көбейтінді үшін 1 - 4 аксиомалары орындалатынын тексеру қиын емес. Сондықтан
кеңiстiгiнде (1) теңдiгiмен анықталған скаляр көбейтінді үшін 1 - 4 аксиомалары орындалатынын тексеру қиын емес. Сондықтан
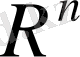 Евклид кеңiстiгiнiң мысалы болады.
Евклид кеңiстiгiнiң мысалы болады.
Евклид кеңiстiгiнде скаляр көбейтiндi арқылы
 элементiнiң нормасын
элементiнiң нормасын
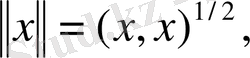 (4)
(4)
теңдiгiмен анықтауға болады.
Анықтама.
Егер әрбір
 үшін нақты сан мәнді
үшін нақты сан мәнді
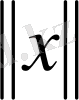 функциясы анықталса және мына шарттарды қанағаттандыратын болса:
функциясы анықталса және мына шарттарды қанағаттандыратын болса:
1)
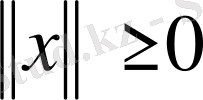 және тек
және тек
 болғанда ғана
болғанда ғана
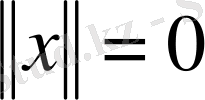 (норманың теріс еместік шарты) ;
(норманың теріс еместік шарты) ;
2) кез-келген
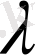 саны үшін
саны үшін
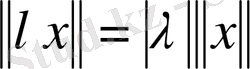 (норманың біртектілік шарты) ;
(норманың біртектілік шарты) ;
3) кез-келген
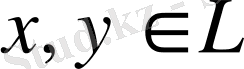 үшін
үшін
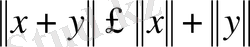 (үшбұрыш теңсіздігі ),
(үшбұрыш теңсіздігі ),
онда
 кеңістігінде
норма
анықталған дейміз.
кеңістігінде
норма
анықталған дейміз.
Дәлелдеуі;
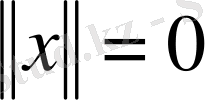 болса, онда барлық
болса, онда барлық
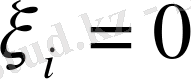 болады. Себебі, егер қайсыбір
болады. Себебі, егер қайсыбір
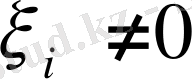 болса, онда (1) теңдігінің оң жағындағы өрнектің мәні оң сан болатыны айқын . Сонымен, егер
болса, онда (1) теңдігінің оң жағындағы өрнектің мәні оң сан болатыны айқын . Сонымен, егер
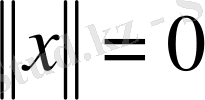 болса, онда
х
векторының барлық координаттары нөлге тең :
болса, онда
х
векторының барлық координаттары нөлге тең :
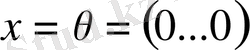 . Керісінше егер
. Керісінше егер
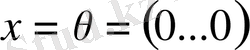 болса, онда
болса, онда
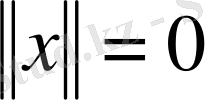 екені айқын.
екені айқын.
Норманың бiрiншi аксиомасы скаляр көбейтiндiнің төртiншi аксиомасынан тiкелей шығатыны айқын. Норманың екiншi аксиомасы орындалатыны да скаляр көбейтiндiнiң үшiншi қасиетiнен тiкелей шығады:
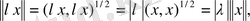
Енді (4) теңдiгiмен анықталған норма үшбұрыш теңсiздігін қанағаттандыратынын дәлелдейiк. Сол мақсатпен кез-келген
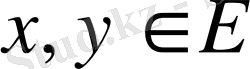 элементтерi және кез-келген
λ
саны үшiн
элементтерi және кез-келген
λ
саны үшiн
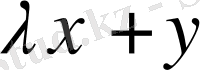 элементiнiң скаляр квадратын қарастырайық:
элементiнiң скаляр квадратын қарастырайық:
 (5)
(5)
Скаляр көбейтiндiнiң 4-аксиомасы бойынша элементтiң скаляр квадраты терiс емес сан, демек,
λ
санының мәнi қандай болса да
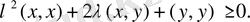 Басқаша айтқанда, квадрат үшмүшенің дискриминанты оң сан емес:
Басқаша айтқанда, квадрат үшмүшенің дискриминанты оң сан емес:
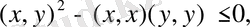 яғни
яғни
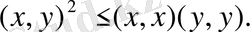 (6)
(6)
Осы теңсiздiктiң екi жағынан квадрат түбiр алып, мына түрде жазайық:
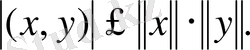 (7)
(7)
Соңғы теңсiздiктен скаляр көбейтiндiнiң абсолют шамасы көбейткiш векторлардың нормаларының көбейтiндiсiнен аспайтынын көремiз. Бұл (7) теңсiздігi Шварц теңсiздiгi деп аталады.
Ендi үшбұрыш теңсiздiгiнiң дәлелiне оралайық. (5) тендiгiнде λ= 1 болғанда, норманың анықтамасы (4) бойынша мына теңдiкке келеміз:
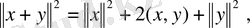
осыдан (7) теңсiздiгiн қолданып, келесi теңсiздiктi аламыз
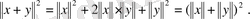 (8)
(8)
Екi жағынан квадрат түбiр алса, (8) теңсiздiгiнен үшбұрыш теңсіздiгi шығады.
Осымен (4) теңдiгi арқылы норма анықталатыны дәлелдендi. Бұл норманы Евклид кеңiстiгiндегi табиғи норма деп атаймыз.
Евклид кеңiстiгiнде табиғи норма анықталғандықтан онда
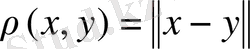 метрикасы анықталған, демек, Евклид кеңiстiгi- метрикалық кеңiстiк.
метрикасы анықталған, демек, Евклид кеңiстiгi- метрикалық кеңiстiк.
Евклид кеңiстiгiнiң мысалдары.
1.
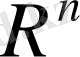 . Бұл кеңiстiкте скаляр көбейтiндi (1) теңдiгiмен анықталғаны белгiлi.
. Бұл кеңiстiкте скаляр көбейтiндi (1) теңдiгiмен анықталғаны белгiлi.
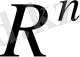 кеңiстiгiнде анықталған Евклид нормасы мен осы пунктте (4) теңдігiмен анықталған норма бiрдей екенi айкын:
кеңiстiгiнде анықталған Евклид нормасы мен осы пунктте (4) теңдігiмен анықталған норма бiрдей екенi айкын:
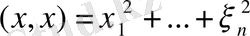 . Мұндай жағдайда норманың екi анықтамасы өзара үйлесiмдi деймiз.
. Мұндай жағдайда норманың екi анықтамасы өзара үйлесiмдi деймiз.
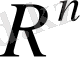 кеңістігiнiң Евклид метрикасы бойынша толық екендiгi дәлелдi . Сонымен,
кеңістігiнiң Евклид метрикасы бойынша толық екендiгi дәлелдi . Сонымен,
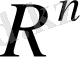 - ақырлы өлшемдi, толық Евклид кеңістігі.
- ақырлы өлшемдi, толық Евклид кеңістігі.
2.
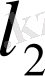 . Бұл кеңістікте кез-келген екі элемент
. Бұл кеңістікте кез-келген екі элемент
 және
және
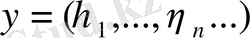 үшін скаляр көбейтіндіні
үшін скаляр көбейтіндіні
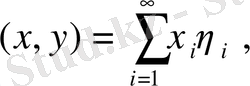 (9)
(9)
теңдігімен анықтайық. Қатарлар үшін Коши теңсіздігінен бұл (9) қатарының кез-келген
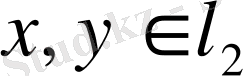 элементтері үшін жинақты екенін қорытамыз. Скаляр көбейтіндінің аксиомалары орындалатыны да айқын. Осы скаляр көбейтiндi аркылы (4) теңдiгiмен анықталған табиғи норма
элементтері үшін жинақты екенін қорытамыз. Скаляр көбейтіндінің аксиомалары орындалатыны да айқын. Осы скаляр көбейтiндi аркылы (4) теңдiгiмен анықталған табиғи норма
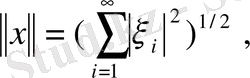 (10)
(10)
((12) ) теңдiгiмен анықталған нормамен үйлесiмдi. Ал бұл норма арқылы анықталған метрика бойынша
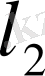 толық кеңiстiк (ІІ. 3) . Демек
толық кеңiстiк (ІІ. 3) . Демек
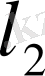 өлшемi ақырсыз, толық Евклид кеңiстiгiнiң мысалы болып табылады.
өлшемi ақырсыз, толық Евклид кеңiстiгiнiң мысалы болып табылады.
Ендi толық емес Евклид кеңiстiгiнiң бiр мысалын келтiрейiк.
3.
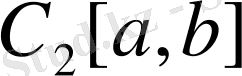 .
.
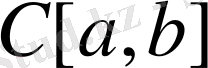 сызықтық кеңiстiгiнiң кез-келген элементтері x(t)
сызықтық кеңiстiгiнiң кез-келген элементтері x(t)
және у(t) үзiлiссiз функцияларының скаляр көбейтiндісiн
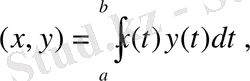 (11)
(11)
теңдiгiмен анықтайық. Бұл анықтама скаляр көбейтiндінiң аксиомаларына сай екенiн тексеру қиын емес. Скаляр көбейтінді (11) теңдiгiмен енгiзiлген
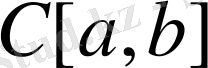 жиыны Евклид кеңiстігіне айналады. Осы кеңiстiктi
жиыны Евклид кеңiстігіне айналады. Осы кеңiстiктi
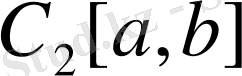 түрiнде белгiлейiк. Мұндағы табиғи норма
түрiнде белгiлейiк. Мұндағы табиғи норма
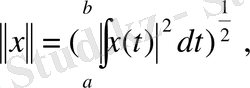 (12)
(12)
екендігі (11) теңдігінен айқын. Бұл норма бойынша
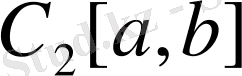 кеңістігінде анықталған метрика
кеңістігінде анықталған метрика
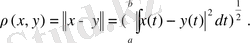 (13)
(13)
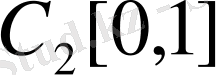 кеңістігінде
кеңістігінде
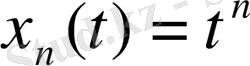 функцияларының тізбегін қарастырайық. Егер тізбек нөмірлері
функцияларының тізбегін қарастырайық. Егер тізбек нөмірлері
 және
және
 болса, онда
болса, онда
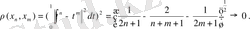
Демек,
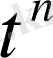 функциялары
функциялары
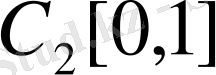 кеңiстiгiнде фундаменталь тiзбек болғаны. Ал [0, 1] кесiндiсiнде
кеңiстiгiнде фундаменталь тiзбек болғаны. Ал [0, 1] кесiндiсiнде
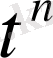 тiзбегi әр нүктеде жинақты, бiрақ оның шегi үзiлiстi функция, яғни
тiзбегi әр нүктеде жинақты, бiрақ оның шегi үзiлiстi функция, яғни
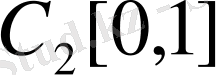 кеңiстiгiне жатпайды. Демек,
кеңiстiгiне жатпайды. Демек,
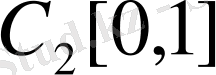 толық кеңiстiк емес.
толық кеңiстiк емес.
Анықтама. Өлшемi ақырсыз, толық Евклид кеңiстiгi Гильберт кеңiстiгi деп аталады.
Мұнан әрi бiз бұл кеңiстiктi Н әрiпiмен белгiлеймiз және тек сепарабель кеңiстiктердi қарастырамыз. Сонымен, келесiде Н арқылы белгiленген кеңiстiк мына шарттарға сай екенiне зейiн салайық:
1) Н - скаляр көбейтiндi анықталған сызықтық кеңiстiк, яғни Евклид кеңiстiгi;
2)
Н
- скаляр көбейтiндi арқылы анықталған нормаға сәйкес
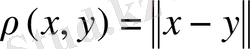 метрикасы бойынша толық кеңiстiк;
метрикасы бойынша толық кеңiстiк;
З) Н - өлшемi ақырсыз кеңiстiк;
4) Н - сепарабель кеңiстiк.
Жоғарыда келтiрiлген Евклид кеңiстiктерiнiң мысалдарынан тек
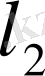 кеңiстiгi ғана осы шарттардың бәрiне де сай, демек
кеңiстiгi ғана осы шарттардың бәрiне де сай, демек
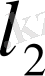 Гильберт кеңiсiтігi екенiн көремiз.
Гильберт кеңiсiтігi екенiн көремiз.
Бұл кеңiстiк Евклид кеңстiгiнiң дербес жағдайы болғандықтан, мұнда да норма (4) теңдiгiмен анықталған. Н нормаланған сызықтық кеңiстiк болғандықтан, жоғарыда метрикалык және нормаланған сызықтық кеңiстiктер үшiн енгiзiлген ұғымдар мен дәлелденген тұжырымдар мұнда да орын алады. Оған қоса, Н кеңiстiгiне тән ұғымдар мен тұжырымдарды ендi қарастыра бастаймыз.
Гильберт кеңiстiктерi математикалық теорияларда кең орын алады.
Алдымен бұрын анықталған кейбiр ұғымдардың Н кеңiстiгiнде қандай түрде болатынына зейiн аударайық.
Н
кеңiстiгiнде
 тiзбегi
х
элементіне жинақталады дегенiмiз,
тiзбегi
х
элементіне жинақталады дегенiмiз,
 кезде
кезде
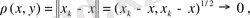
яғни
 айырымының скаляр квадраты нөлге ұмтылады деген сөз.
айырымының скаляр квадраты нөлге ұмтылады деген сөз.
Скаляр көбейтiндi өзiнiң екi аргументi бойында үздiксiз функция екенiн дәлелдейiк.
Шынында да, егер
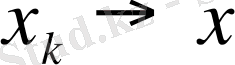 және
және
 болса, онда скаляр көбейтiндiнiң аддитивтiк қасиетiн және Шварц теңсiздiгiн пайдаланып,
болса, онда скаляр көбейтiндiнiң аддитивтiк қасиетiн және Шварц теңсiздiгiн пайдаланып,
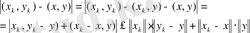
теңсiздігiне келемiз. Ал мұнда
 шенелген тiзбек, себебi
шенелген тiзбек, себебi
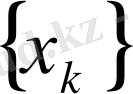 i шегi бар тiзбек. Шарт бойынша
i шегi бар тiзбек. Шарт бойынша
 кезде
кезде
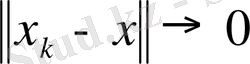 және
және
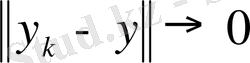 демек,
демек,
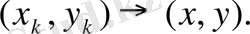
2. Скаляр көбейтiндiлi кеңiстiктегi геометрия
Скаляр көбейтiндi арқылы Евклид кеңiстiгiнде геометриялық ұғымдар енгiзiледi және, осыған байланысты, геометриялық мазмұнды фактылар айкындалады.
1
. Вектордың ұзындығы
.
 векторының ұзындығы деп
векторының ұзындығы деп
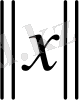 санын айтамыз.
санын айтамыз.
2.
Екi вектордың арасындағы бұрыш
. Екi
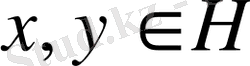 векторларының арасындағы
векторларының арасындағы
 бұрышының косинусы
бұрышының косинусы
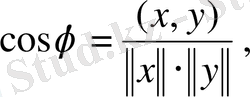 (2. 1)
(2. 1)
теңдігімен анықталады.
Шварцтың (1. (7) ) теңсiздiгiнен (2. 1) тендiгiнiң оң жағында тұрған бөлшектiң абсолют шамасы 1-ден аспайтыны шығады, сондықтан ол санды бұрыштің косинусы ретiнде алуға болады.
Евклид кеңiстiгiнiң кез-келген екi элементi (векторлары) арасындағы бұрыш анықталуына байланысты екi элементтің ортогонал болу шарты анықталады:
Егер
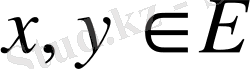 элементтерiнiң скаляр көбейтіндiсi
элементтерiнiң скаляр көбейтіндiсi
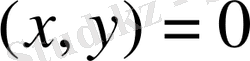 болса,
х
пен
у
өзара ортогонал векоторлар деп аталады. Бұл анықтама бойынша, ортогонал элементтердiң (векторлардың) арасындағы бұрыш
болса,
х
пен
у
өзара ортогонал векоторлар деп аталады. Бұл анықтама бойынша, ортогонал элементтердiң (векторлардың) арасындағы бұрыш
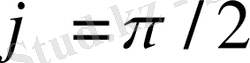 болғаны.
болғаны.
Егер
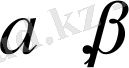 - кез-келген нақты сандар болса, онда
- кез-келген нақты сандар болса, онда
 (2. 2)
(2. 2)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz