ФИЗИКАДАН ЕСЕПТЕР ШЫҒАРУДЫҢ МАҢЫЗЫ

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 60 бет
Таңдаулыға:

МАЗМҰНЫ

КІРІСПЕ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . 3

I ФИЗИКАДАН ЕСЕПТЕР ШЫҒАРУДЫҢ МАҢЫЗЫ ... ... ... ... ... ... .7

1. Физика есептері және олардың
түрлері ... ... ... ... ... ... ... ... ... ... ... ..7

2. Физика есептерін шығару
методикасы ... ... ... ... ... ... . ... ... ... ... ... ... .11

3. Физика шамаларының өлшеу
бірліктері ... ... ... ... ... ... . ... ... ... ... ... ... ... .

ІІ МЕХАНИКА БОЙЫНША ЕСЕПТЕР ШЫҒАРУ ... ... ... ... ... ... ... . ... ...22

2.1 Механика бойынша есептер шығарудың ерекшеліктері
... ... ... ... ... .22

ҚОРЫТЫНДЫ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .27
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР ТІЗІМІ ... ... ... ... ... ... ... ... ... ...

Кіріспе

Қазіргі заманда ғылым мен техниканы бір-бірінен ажыратып бөлуге
болмайды, бірін білмейінше, екіншісін меңгеру қиын. Тіпті қарапайым
техниканың өзін меңгеру үшін физика негіздерін білетін, оны іс жүзінде
саналы түрде қолдана алатын адам керек. Ғылым мен техниканың ұштасып, бір-
бірімен байланысты екенін мынадай мысалдардан көруге болады: атом
энергетикасы, космос кеңістігін игеру, зерттеу; жартылай өткізгіштер
дүниесі, лазерлер, мазерлер, кибернетика мен бионика сияқты жаңа
бағыттардың дамып, өндіріске келуі - оны игеретін, іске қосатын адамның,
демек, келешектегі жастардың білімді болуын талап етеді.
Жаратылыстану пәндеріне оның ішінде физика пәнінің мектепте оқытылу
жайына көңіл аудару – тәуелсіз еліміздің болашақ мамандары үшін аса
маңызды. Елімізде 300-дей мамандық түрлері бар десек, соның 80 пайызынан
астамы түрлі сала инженерлері, ауылшаруашылық мамандары. Ендеше мектеп
қабырғасынан бұл пәндерді терең меңгермеген адамнан келешекте нашар маман
шығатыны еш күмән туғызбайды. Кеңес заманынан бері бұл пәнге берілген сағат
қысқартыла берді. Осының салдарынан физика пәнін оқытуда есептер шығаруға,
лабораториялық жұмыстар жасауға аз уақыт бөлінеді. Осыдан оқушылардың
физика пәніне деген қызығушылығын және оны оқыту сапасын қалай арттыруға
болады деген сұрақ туындайды.
Қазақстан Республикасындағы экономикалық өсудің маңызды ресурстары мен
интеллектуалды білім беру әлеуеті оның әлемдегі рөлін анықтайды. Кез-келген
мемлекет үшін қоғамның болашағын қалыптастыру міндеттері ең алдымен жас
жеткіншектерге ғылым негіздерінен заман талаптарына сай білімдер беру мен
тәрбиелеу жұмыстарынан басталады.
Зерттеу мақсаты: физиканың идеяларын, заңдарын оқушыларға тиісті дәрежеде
жеткізудің жолдарын анықтау, оқушылардың теориялық білімдерін есеп
шығарумен ұштастыру жолдарын табу. Физикадан есептер шығару оқушылардың
алған білімін бекітуге, ойлауын дамытуға, физикаға қызығуын арттыруға,
проблемалық оқытуға жағдай жасауға қолданылуын түсіндіру және физикадан
есептердің классификациясын беру.
Соңғы он жылдың ішінде орта мектеп көлемінде оқылатын физика курсы
түбірімен өзгерді, жаңартылды, оның теориялық мазмұны жоғары сатыға
көтерілді, физика ілімінің соңғы жетістіктері еске алынды. Мысалы, кванттық
теория, салыстырмалық теория негіздері енгізілді, классикалық механиканың
математикалық негіздері арттырылды. Жалпы алғанда, жаңа курстардың
методологиялық жағы да күшейтілді. Осыған байланысты, мектеп қабырғасында
физиканы оқыту мәселесі күрделі проблемаға айналып отыр. Соңғы бірнеше жыл
ішінде, орта мектепте, физика курстарын оқыту тәсілдерін көрсетіп беретін
методикалық әдебиеттер жарық көрді. Мысалы, физиканың барлық салалары
бойынша, программаға сай, көмекші құралдар, дидактикалық материалдар
жасалды. Демек, физиканың идеяларын, заңдарын оқушыларға тиісті дәрежеде
жеткізудің жолдары анықталды.
Зерттеу міндеті: Физика пәнінің әр түрлі есеп жинақтарына талдау жасау,
механика бойынша ұсынылған есептерді сұрыптап, есеп шығарудың әдістемесін
анықтау.
Физикалық теорияны үйретуде, оның мағынасын терең түсіндіріп пайдалану
жолдарын іздестіруде, оқушыларға жаттығу ретінде сыныпта, үйлерінде өз
күшімен түрлі есептер шығартудың мәні ерекше. Курстық жұмыста механика
бойынша есептер шығарудың түрлі жолдары көрсетілген.

I. ФИЗИКАДАН ЕСЕПТЕР ШЫҒАРУДЫҢ МАҢЫЗЫ

1.1. Физика есептері және олардың түрлері
Физика есебі дегеніміз – физика тақырыптары бойынша құрылған, шешуді
қажет ететін сұрақтар мен проблемалар. Физика есептерінің түрлері көп, оны
шығарудың тәсілдері жан-жақты. Мұның себебі, физика программасында
қарастырылатын мәселелер өте көп әрі көлемді. Сондықтан да физика
есептерін шығару күрделі мәселе. Дегенмен де, оқу программасын меңгеру
үшін, мұндай жаттығулар керек-ақ. Оқушы тақырып бойынша есеп шығара
алмайтын болса, ол физиканы терең түсінеді деп айту қиын.
Физика есептерін шығару үшін теориялық мәселелерді түсініп, іс
жүзінде падалана білу керек, демек, шығармашылық еңбек ете білуі, терең
ойланып, күрделі мәселелерді шеше алатындай болуы керек. Физика есебін
шығаруда оқушылар көптеген құбылыстардың заңдарын анықтайды, теорияның
мағынасын терең түсініп, өмірдегі рөлін көреді. Есеп шығаруда оқушылар
техниканың жаңалықтарымен танысады, физикалық негіздерін анықтайды, жалпы
білімдерін көтереді, сөйтіп политехникалық тәрбие алады.
Физика есебін шығаруда оқушылар теориялық мәселелерді бір емес,
бірнеше рет қайталайды, осының нәтижесінде физикалық құбылыстар, заңдар
ойда сақталып қалатындай жағдай туады. Есеп шығару кезінде оқушылар
физикамен бірге өздерінің математикалық дайындығын жақсартады. Физика
есептері математиканы жандандырады, оның мағынасын арттырады. Математикалық
түрлендірулер физикалық теңдеулерге, формулаларға ауысқанда оның әрбір
бөлігінде күнделікті іс-тәжірибеде мағынасы бар шамалар пайда болады.
Функционалдық тәуелділіктің мағынасы тереңдетіліп, графиктік байланыстар
физика құбылыстарының динамикасын ашып айқындауға көмектеседі, оның
көрнекілік жағы күшейтіледі. Физика есептерін шығарумен бірге оқушылар
есептеу техникасын үйренеді.
Қорыта келгенде, оқушылар физика есептерін шығаруға дағдыланып,
үйренсе, теориялық біліктерін практикамен ұштастыра алатын болады. Оқушылар
мұндай дәрежеге жету үшін, мектеп қабырғасында, одан тыс көптеп есептер
шығарулары керек. Оқушылар есепті қызығып шығаруы үшін оның мазмұны
тартымды, бірақ әрқашан да өмірге жақын болуы керек.

Физика есептерінің түрлері.
Физика есептері мазмұнына қарай әр түрлі тақырыптарды қамтуы
мүмкін. Сондықтан да, есептер қаралатын проблемаларға, құбылыстарға
байланысты: механикалық, молекулалық физика, электромагнетизм, атомдық және
ядролық физика есептері деп бөлінеді.
Есеп жалпы құрылысына қарай, қойылған сұрақтарға, шешу
тәсілдеріне қарай ауызша, сапалық, мәселе есептер, эксперименттік, қызықты
есептер болып бірнеше түрге бөлінеді. Әрбір тақырып бойынша есептерді
белгілі бір ретпен шығару қажет. Осы есептердің түрлерін қарастырайық
1) Ауызша-сұрақ және сапалық есептер - құрылысы қарапайым, ауызша
жауап беретіндей етіп құрастырылады. Бұл есептерді шешу үшін
қарапайым құбылыстардың заңдылықтарын білу керек. Ауызша есептер,
көп жағдайда, графиктердің физикалық мағынасын анықтау не
схемалардың бөліктерін талдау түрінде беріледі.
Ауызша есептер, көбінесе, өткен сабақта берілген заңдылықтарды
еске түсіру үшін, қайталау үшін, жаттығу түрінде қолданылады. Әдетте, сұрақ
есептер бүкіл сыныпқа беріледі, оқушылар теориялық білімдерін саналы түрде,
іс жүзінде пайдалану жөнінен алғашқы қадам жасайды.
2) Мәселе есептер – бір не бірнеше оқиғаларды қамтитын,
математикалық түрде шешілетін проблемалар түрінде беріледі. Демек, есепті
толық шешу үшін математикалық түрлендірулер, есептеулер жүргізу керек.
Мәселе есептер, әдетте, бірнеше заңдылықтарға бағынатын оқиғаларды
қарастырады. Оны шығару үшін келтірілген құбылыстарды талдап, бір-бірімен
байланысын анықтап, заңдарын жазып, проблемаларға сай теңдеулер қорытып
шығарып, ақырында математикалық есептеулер орындау керек.
3) Эксперименттік есептер - құрылысы жағынан, шығару тәсілдері
бойынша, мәселе есептерге ұқсас, бірақ қажетті шамалар тәжірибе нәтижесінде
алынады. Оқушылар мұндай есептерді шығару үшін қойылған проблемаға
байланысты қажетті заңдылықтарды анықтап, өз күшімен тәжірибелер жүргізеді,
өлшеулер жасайды. Қажетті шамалар алынғаннан кейін, эксперименттік есеп
мәселе есепке айналады. Физиканы оқып үйренуде, оның мағынасын терең
түсінуде, экспиременттік есептер орындаудың орны ерекше. Оқушылар құрал-
жабдықтармен танысып, өлшеулер жасау техникасын үйренеді, жаттығулар
орындайды да, физика құбылыстарын қолдан жасап, көзімен көреді. Тіпті
қарапайым тәжірибенің өзін қызығып жасайтын болады. Тәжірибені
қорытындылау, заңдылықты табу, оны қайта ашумен бірдей. Мұндай жағдай
оқушыны қуантпай қоймайды.
4) Қызықты есептер - табиғатта, өмірде кездесетін таң қаларлық
оқиғалардың табиғатын анықтауға негізделген. Бұл есептер талқыланып ауызша
шығарылады, тек кейде мәселе есепке айналады.

2. Физика есептерін шығару методикасы
Физика есептерін шығару тәсілдері көп-ақ. Есептің мазмұнына
қарай, қойылған мәселелерге, сұрақтарға қарай, жеңіл, орташа дәрежедегі
қиындығы бар, қиын есептер болып бөлінеді. Сондықтан да оқушылар, тақырып
бойынша, әуелі жеңіл дегендерін, оның ішінде ауызша-сұрақ есептерін,
сапалық есептерді шығарып жаттығулары керек. Бұл - тақырып бойынша берілген
заңдардың физикалық мағынасын тереңірек түсінуге көмектеседі; оларды
нақтылы жағдайда қолдана білу мәселелерін үйретеді. Осыдан кейін есептің
барлық түрлерін шығарып машықтану керек. Есеп құралдарында келтірілген
жаттығулардың өзі осы негізде құрылған. Демек, кітаптағы әрбір тақырыптың
бас жағында сұрақ-есептер, не жеңіл мәселе есептер беріледі. Әдетте, мәселе
есептің өзі құбылыстарды, формулаларда, өлшеу бірліктерін еске түсіру үшін,
тәжірибе алу үшін беріледі. Әрі қарай есептер мазмұны жағынан да, шығару
тәсілі бойынша да қиындай түседі. Күрделі есептер, әдетте, тақырыптың аяқ
жағында келтіріледі. Жекелеген есептердің мазмұны, түрлері әр түрлі
болғанымен, жалпы есептердің белгілі бір реті бар. Көптеген тәжірибелер
есеп шығарғуда мынандай схеманы ұстану тиімді екенін көрсетеді.
1) Есептің шартымен танысу. Бұл мәселеге ерекше көңіл бөлу керек.
Оқушы есепте қарастырылып отырған мәселелерді толық ұғынып, қойылған
сұрақтарды анық түсінуі керек. Мұнда техника мен өндіріске қатысты
терминдерді белгілеп, олардың мағынасын анықтап алулары қажет. Есептің
шартына байланысты берілген шамаларды, сұрақтарды, қосымша тұрақтыларды
(константаларды) қысқаша таңбалап жазу керек. Эксперименттік есеп болса,
қажетті құрал-жабдықтарды алдын ала түгендеп, жұмыстық күйін тексеріп алуы
керек.
2) Есептің мазмұнын талқылау. Есептің шартында берілген
шамаларды қарастырғанда оларды физиканың қай бөліміне жататынын тауып,
құбылыстардың арасындағы байланыстарды, әрқайсысының заңдылығын анықтау
керек те, формулаларын жазуы тиіс. Күрделі оқиғаларды жеке-дара
құбылыстарға жіктеп, қарапайым түрге келтіруі керек. Барлық жағдайда
координаталар системасын ыңғайлы етіп алып, берілген шамалардың
бағыттарын, кеңістіктегі орнын анықтау керек. Мүмкіндігі болса, оқиғаның
суретін салу, оның графигін сызу - есепті талдау үшін, заңдылықтарын ашу
үшін өте қажет.
3) Есепті жалпы түрде шығару. Есептің жалпы сұрауына жауап
берудің жолдарын іздестіріп, проблеманы анықтайтын теңдеуді қорытып шығару
керек. Сұраққа жауап беретін формулалардан бастап, басқа тәуелділіктерді
пайдалана отырып, қорытынды формуланы шығарып алу, мүмкіндігінше бұл
теңдеуді алгебралық жолмен шығарып алып, содан кейін ғана сан мәндерін
орындарына қойған жөн. Барлық жағдайда бір ғана қорытынды формула шығару
міндет емес, кейде есепті бөлшектеп шығару ыңғайлы болады. Эксперименттік
есепті шығару үшін, әуелі тапсырма бойынша тәжірибелер жүргізіп, қажетті
шамаларды алу керек. Содан кейін осы шамаларды бір-бірімен салыстыру
нәтижесінде, графиктік тәуелділікті көрсету арқылы, белгілі заңдылықтармен
салыстыра отырып, қорытынды шығару керек. Осындай қорытындылаудан жаңа
заңдылық шығуы мүмкін. Оқушылар үшін мұндай шешім өте пайдалы. Біраз
жағдайда, өлшемдер алынғаннан кейін, жалпы формуланы іздестіру керек
болады.
4) Есептеу. Есепте берілген шамалардың барлығын СИ өлшемдеріне
келтіру қажет. Сан мәндері өте үлкен не өте кіші болса, дәреже түрінде
жазып, есептеу керек. Барлық жағдайда да шамалардың дәлдігін ұмытпау қажет.

Мүмкіндігі болса, арифметикалық жұмысты шағын электронды есептеу
машинасымен, не логарифмдік линейкамен жүргізген жөн. Бірақ бұлардың бәрі
оқушылардың өздері есептей білуді толық меңгергеннен кейін ғана қолданады.

5) Есептің жауабын тексеру. Біріншіден, есептің жауабы шындыққа
жақын болуы тиіс. Мысалы, автобустың жылдамдығы есептеу нәтижесінде 50 мс
болсын делік, сонда оны кмсағ-қа айналдырғанда 180 кмсағ болып шығады;
әрине, бұл шындыққа жатпайды. Демек, есеп дұрыс шығарылмаған. Есептің
нәтижесін тексеру үшін берілген жауабын қарауға болады.

1.3. Физика шамаларының өлшеу бірліктері
1960 жылдан бастап, халықаралық өлшеуіштер мен таразылар жөніндегі ХІ
Бас конференцияның шешімі бойынша, негізгі өлшеуіштер ретінде алғашқы 6
шаманың бірліктері енгізілген болатын. Қазіргі кезде, Халықаралық бірліктер
системасына (СИ), физикалық шамаларды анықтау үшін не бары 7 шаманың
бірліктері енген.
Бұлар:
1. ұзындық бірлігі – метр (м)
2. масса бірлігі - килограмм (кг)
3. уақыт бірлігі – секунд (с)
4. ток күші бірлігі – ампер (А)
5. термодинамикалық температура бірлігі - кельвин (К)
6. зат мөлшері – моль (Моль)
7. жарық күші бірлігі – канделла (Кд)
косымша бірліктер:
8. жазық бұрыш бірлігі – радиан (рад)
9. денелік бұрыш бірлігі – стерадиан (ср)
Бұлар негізгі бірліктер қатарына жатқызылған. Қалған физикалық
шамалардың өлшеу бірліктері осы негізгі бірліктерден туынды ретінде
табылады. Ол үшін физикалық шаманы анықтайтын теңдеуді жазып, құрамындағы
шамалардың бірліктерін қоямыз. Мысалы:
не
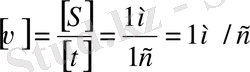
Бұл туынды бірліктері секундына метр деп оқиды. Осы сияқты барлығы 70-
тен астам туынды бірліктер бар. Оның 17-не арнайы атаулар берілген: 15-іне
атақты ғалымдардың аттары берілген, қалған екеуі - люкс (лк), люмен (лм)
деп аталады. Ғалымдардың аттарымен аталған бірліктер үлкен әріппен
жазылады, мысалы: Н (ньютон), Гц (герц), Па (паскаль), Дж (джоуль), Вт
(ватт), Кл (кулон), В (вольт), Ф (фарад), См (сименс), Ом (ом), Вб (вебер),
Тл (тесла), Гн (генри), Бк (беккерель), Гр (грей).
СИ системасының туынды бірліктерімен бірге, пайдалануға болатын
қосымша 19 бірлік бар, бұлар: тонна, минут, сағат күн, бұрыштық градустар
және оның бөліктері: цельсий градусы (оС), диоптрия (оптикада), массаның
атомдық бірлігі (м.а.б.), электронвольт – (эВ) .
Есеп шығаруда қорытынды формулаға жай сандардың өзін жаза салуға
болмайды, міндетті түрде цифралардан кейін туынды бірлікті жазу керек.
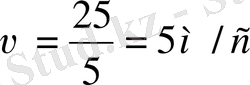
Мысалы: деп жазу дұрыс емес, ортадағы шамалардан кейін (мс)
бірлігін қосып жазу керек.
Берілген шамаларды есептеуге ынғайлы болу үшін, сан мәндерін СИ
систамасында жазғанда, оларды дәреже көрсеткіштері арқылы өрнектеген жөн,
ал қорытынды шаманы қысқаша, үлестік таңбамен жазуға болады. Мысалы:
берілген шамалар мындай болсын:

Берілгені:

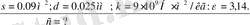
Есептеу формуласына қою үшін, сандарды былай жазамыз

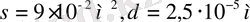
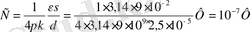
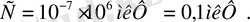
Қорытынды шаманың мәні, 02 ... 1000 сандарының арасында болса, өзін
жаза салу керек, ал қалған жағдайларда үлестік таңбаларды қолданған жөн.
Мысалы: есептей келгенде мынадай шамалар шықты дейік: 10-3 м, 100 000 кВт.
Бұларды былай жазған ыңғайлы: 1 мм, 100мВт. Осы жағдайды жоғарыдағы
есептеуде қолдандық.

Мақсаты: Суға тұзды салғанда судың қайнау температурасына әсер ететін
факторларды жорамалдай отырып, тұз ерітіндісіне зерттеу жүргізу.

Гипотеза: Суға тұзды салғанда оның қайнау температурасы өзгереді. Оған
келесі факторлар әсер етуі мүмкін:

• тұздың температурасы бөлме температурасына тең болуы;

• тұз ерігенде жылуды жұтуы;

• тұз ерігеннен кейін ерітіндінің қайнау темературасы судың қайнау
температурасынан өзгеше болуы мүмкін.

Қайнау – сұйықтықтың тұтас көлемінде бу көпіршіктерінің пайда болып,
олардың сұйық бетіне шығып буға айналуы. Сұйықтықты қыздырған кезде оның
ішіндегі көпіршіктерінің көлемі ұлғайып, біртіндеп жоғары қалқып шығып
жарылады да, ол сұйық бетіндегі бу фазасына айналады. Сұйықтық бетіндегі
будың қысымы сыртқы қысымға теңелгенде қайнау процесі басталады.
Сұйықтықтың үнемі қайнап тұруы үшін оған қажетті жылу берілуі тиіс, ол бу
фазасы көлемінің ұлғаюы кезінде – бу түзілуі мен будың сыртқы қысымға қарсы
жұмысына жұмсалады. Тұрақты қысым жағдайындағы сұйықтықтың қайнауы жүретін
температура – қайнау температурасы (Тқ) деп аталады. Қысымның артуымен Тқ
жоғарылайды. Қайнаудың шектік температурасы заттың кризистік температурасы
болып табылады. Химиялық таза заттың атмосфералық қысымдағы қайнау
температурасы – оның негізгі физикалық-химиялық сипаттамаларының бірі.
Сұйықтық құрамындағы әр түрлі өте майда қатты бөлшектер немесе газ
көпіршіктері қайнау орталығы деп аталады. Қайнау орталығы жоқ, яғни алдын-
ала бөгде қоспалардан және еріген газ бөлшектерінен мұқият тазартылған
сұйықтықты қатты қыздырмай, яғни қайнатпай-ақ оның температурасын Тқ-нан
арттыруға болады. Қатты қыздырылған сұйықтық қайнаған кезде қайнау процесі
қауырт өтіп, жарылысқа ұқсас дыбыс шығарады да, оның температурасы өзімен
тепе-теңдікте тұрған қаныққан будың температурасына дейін суынады.
Сұйықтықта пайда болған көпіршік көлемінің артуы үшін оның ішіндегі будың
қысымы сыртқы қысым (көпіршіктен жоғары орналасқан сұйық қабаттарының
қысымы мен көпіршік бетінің қисықтығына тәуелді болатын капиллярлық
қысымның) қосындысынан артық болуы тиіс. Бұл шарт бу мен жылулық тепе-
теңдікте тұрған сұйықтықтың температурасы Тқ-нан артық болғанда ғана жүзеге
асады. Күнделікті тұрмыста жиі кездесетін қайнаудың бұл түрін көпіршікті
қайнау деп атайды. Мұндай қайнау кезінде қыздырылған беттің температурасы
қайнау температурасынан аздап жоғары болады да, қыздырылған беттің
температурасын арттырғанда бу түзілу орталықтары күрт өседі; олардан
бөлініп шыққан көпіршіктер сұйықтық бетіне қалқып шығады да, сұйықтық
қабаттары қауырт араласа бастайды. Көпіршікті қайнау кезінде жылу бөліп
алу, суытудың ең тиімді тәсілі болып саналады. Бұл тәсіл атомдық реакторлар
мен реактивтік қозғалтқыштарды салқындатуда қолданылады. Қайнау процестері
химиялық технологияда, тамақ өнеркәсібінде, сұйытылған газдарды өндіруде,
электрондық құралдардың тетіктерін салқындатуда, т.б. ғылым мен өнеркәсіп
салаларында кеңінен пайдаланылады.

II. Зерттеу бөлімі

Қайнап жатқан суға тұзды сепкенде оның қайнауы тоқтайды. Бұл құбылыстың
себебін қалай түсіндіруге болады?
Біріншіден, тұз температурасы бөлме температурасына тең 200С
Екіншіден, тұз ерігенде жылуды жұтады.
Үшіншіден, судың қайнау температурасы артады.
Су қашан қайта қайнайды?

Бірінші фактор
Бірінші себептің түсіндірмесі:
mс - судың массасы болсын, mт - тұздың массасы болсын,сс - судың
салыстырмалы жылусыйымдылығы болсын, ал ст-тұздың салыстырмалы
жылусыйымдылығы болсын. Судың қайнау температурасын tқ-деп, тұздың
температурасын tт- деп белгілейік.

1.1.Тұзды ерімейді деп алып, су температурасының тұз қосқан кездегі өзгеру
мәнін алдық.Судың жылусыйымдылығын, сс = 4200 Дж(кг•°C), ал тұздың
жылусыйымдылығын тұз ерітіндісінің салыстырмалы жылусыйымдылығының оның
концентрациясына тәуелділік кестесінен аламыз.

1 кесте.Тұз ерітіндісінің салыстырмалы жылусыйымдылығының оның
концентрациясына тәуелділігі.
η, % 0 5 10 15 20 25
c, 4,24,00 3,93,68 3,55 3,36
кДж(кг•°C) 0 0

Тұздың ерітіндегі коцентрациясы келесі формула арқылы анықталады:
η = mтmе, мұндағы mт- тұздың массасы, mе- ерітіндінің массасы.
Осыдан жылу баллансының теңдеуін пайдаланамыз:
ссmс∆t=cтmт(tқ-∆t-tт)

бұдан: ссmс∆t=cтmт(tқ-∆t-tт)

ссmс∆t = cтmтtқ- cтmт∆t - cтmтtт

ссmс∆t+cтmт∆t = cтmтtқ - cтmтtт

∆t(ссmс+cтmт) = cтmт (tқ - tт)

∆t=

1.2. Кестенің көмегімен "араласу заңы" концентрацияның кең көлемдегі
қайнаған тұз ерітіндісіне қолданылатынына көз жеткіземіз, сонымен қатар
салыстырмалы жылусыйымдылығын, ст-ны, табамыз.
Араласу заңы бойынша:
c(mc+mт)=cсmс+cтmт
Теңдіктің екі жағын mс+mт бөлгенде = η, ал = 1- η екенін
байқаймыз.
Бұдан: c()=cc()+ст()

c = cc()+ст()
─────────────────────────────────── ─────
η = = │me = mс+mт│=
1- = 1- η

= 1- η

= 1- η

─────────────────────────────────── ─────

с = сс (1- η) + cт η = cс-(cс-cт)η теңдігін аламыз.

Демек ерітіндінің салыстырмалы жылусыйымдылығының концентрацияға
тәуелділігі сызықтық болып келеді және еңкею коэффиценті k=cc-cт . c(η);
тәуелділік графигі:

Коэффициент k=3300 oС, демек ст=900 oС
1.3. Судың массасы =1,0 кг, судың температурасы =100°С, тұздың
температурасы =20°С. Температураның өзгеруін есептейміз (1.1 пунктінде
алған формуламен).
=20г және =300г.
Бірінші жағдайдағы су температурасының өзгеруі
∆t1= = = 0.34oC

Ал екінші жағдайда:
∆t2= = = 4.8oC

Екінші фактор

Еріту кезінде судың қаншаға салқындайтынын анықтау үшін, біз анықтамалықтан
қайнаған тұздың салыстырмалы жылулығын аламыз. Таңқаларлық, алайда ол
температура судағы тұздың санына байланысты өзгереді екен.

C, г – 1кг судағы тұздың салмағы 10 50 100200 350
q, кДжкг 72,66,2 57,42,5 32,2
3 3

2.1. =1,0 кг суға температурасы -ға тең тұз саламыз.Егер
=20г және =300г болса ерітіндідегі температураның өзгеруін
анықтаймыз.Керекті ұғымды алу үшін сызықтық интерполяция жасауға болады ,
яғни әрбір интервалда салыстырмалы жылу еруі сызықтап өзгереді.

+b

(10;50) интервалы үшін аламыз:
72,3
66.2

Және содан,
72,3
66,2

b= 72,3-10a

66,2 = 50a + 72,3-10a

40a = - 6,1

b

:
q1= = 70,8кДжкг

300г :
q2= = 35,6кДжкг

Тұзды еріту үшін qmт - ға тең жылу қажет. Жылу балансының теңдеуі:
qmт+)t

Осыдан, үшін:
t1= = 0,34C

үшін:
t2= = 1,5C

Үшінші фактор

Келесі қажетті кестенің аты “Тұз ерітіндісінің қайнау температурасы”.
Тұз ерітіндісінің қайнау температурасы.
η, % 0 5 10
0 0 100 0
5 0,053 100,5 0,5
10 0,11 101,0 1,0
15 0,18 101,6 1,6
20 0,25 102,2 2,2
25 0,33 102,9 2,9

t () тәуелділігінің графигі.

Коэффициент α=8,7C.

3.2 mС= 1,0 кг суға mт1 = 20 г және mт2 = 300 г тұз қосқанда қайнау
температурасы қанша градусқа өсетінін анықтаймыз.

Осыдан, үшін:
t1= α = 8,7C * = 0,17C

үшін:
t2= α = 8,7C * = 2,6C

Төртінші фактор

Су қашан қайтадан қайнайды?
4.1. 1 кг таза су бөлме температурасы tт = 20 °C-нан tҚ = 100 °С қайнау
температурасына 5 минутта қызды. mт1 = 20 г және mт2 = 300 г тұз қосқанда
қайнау неше секундтан кейін жаңартылатынын бағалаймыз.Тұздың еруі тез
жүреді деп есептейміз.
Бағалау үшін жалпы эффектті анықтасақ болды.

үшін:

C = 85C

Сол себепті су

t1= ⋅ = ⋅ 0.85C ≈ 3c қайнайды

үшін:

C

Сол себепті су

t2= ⋅ = ⋅ 8.9C ≈ 33c қайнайды

III. Жұмыс барысы

IV.Қорытынды:

Бұл жұмыстың барысында біз суға тұзды қосқан кездегі қайнау
температурасының өзгерісін зерттей келе :

• ерітіндінің салыстырмалы жылусыйымдылығының концентрацияға тәуелділігі
сызықтық болатындығын анықтап және еңкею коэффиценті k=cc-cт .
c(η); тәуелділік графигін тұрғыздық;

=20г тұз қосқанда су температурасының өзгеруі ∆t1=0.34 oС
=300г. тұз қосқанда су температурасының өзгеруі
∆t2=4.8 oС
• Тұз еруге қажет жылуды анықтадық және ерітіндідегі температураның
өзгеруін анықтадық

үшін: 0.34C
үшін: 1.5C
• Тұз ерітіндісінің қайнау температурасын анықтадық:

үшін: 0.17C
үшін: 2.6C
• Судың қайтадан қашан қайнайтынын анықтадық:

үшін t1= 3c қайнайды

үшін t2= ≈33c. қайнайды

II. Механика бойынша есептер шығару

Механика үш бөлімге бөлінеді: кинематика, динамика, статика.
Кинематика қозғалыстың геометриясын зерттейді. Қозғалыстың
геометриясы дегеніміз - денелердің қозғалысын оларды тудыратын себептерді
қарастырмай, математикалық сипаттау.
Кинематикалық есептерді шығарған кезде әрекеттерді келесі ретпен
орындау керек:
1. Есепті мұқият оқып шығып, шартын талдау;
2. Берілген шамалардың негізгі мәндерін талдау барысында
анықталған қосымша шамаларды жазып алу;
3. Есеп берілген қозғалысты сипаттайтындай етіп схемалқ сызба
жасау. Онда қозғалыс траекториясын, жылдамдық векторын, үдеуді,
орын ауыстыруды бейнелеу,
4. Санақ денесімен байланысты координат жүйесін таңдау, координат
осьтерінің оң бағтын кзрсету;
5. Есепті жүргізу үшін теңдеулердің скалярлық формасын жасау керек,
яғни координат осіне проекциясы түрінде;
6. Құрылған теңдеулер жүйесін ізделініп отырған шамаларға қатысты
шешу, яғни есептеуіш формулаларды табу;
7. Нәтижелерді талдап, нақты жауабын жазу.
Траекториясы түзу сызық болатын қозғалыс түзу сызықты қозғалыс деп
аталады. Траекториясы қисық сызық болатын қозғалыс қисық сызықты қозғалыс
деп аталады (мысалы, шеңбер бойымен қозғалыс). Траектория бойымен
есептелетін қашықтық жол деп аталады. Жол скаляр шама, себебі ол қозғалыс
бағытын көрсетеді.
Егер дене бірдей уақыт ішінде бірдей жол жүрсе, онда оның қозғалысы
бірқалыпты болады.
Бірлік уақыт ішінде жылдамдық тұрақты шамаға өзгеретін қозғалыс
бірқалыпты айнымалы деп аталады.
Түзу сызықты қозғалыс динамикасынан есептерді шығарған кезде келесідей
қадамдарды жасаған дұрыс:
1. Алдымен денеге әсер ететін күштерді анықтап, оларды сызбада
көрсету керек;
2. Координат системасын таңдау;
3. Ньютонның екінші заңына сүйене отырып, әрбір дене үшін күш
проекциялары мен үдеуді байланыстыратын қозғалыс теңдеулерін
құру керек. Егер берілген есепте денелер қозғалысы өзара
байланысты болса, онда осы байланысты бейнелейтін кинематикалық
шамалар үшін теңдеулер жазу керек;
4. Алынған теңдеулер жүйесінің ізделінетін шамаларға қатысты
шешімін табу.
Ньютонның екінші заңы дененің үдеуін ғана табуға мүмкіндік береді.
Денелердің жылдамдығы мен координаттары бастапқы шарттарда берілсе ғана
анықталады.
Шеңбер бойымен бірқалыпты қозғалыс динамикасының есептері түзу сызықты
қозғалыс дмнамикасының есептері сияқты шығарылады. Бірақ олар арасында
айырмашылық бар: шеңбер бойымен қозғалтын дененің үдеуі оның центріне қарай
бағытталады.
Динамика – дененің өзара әсерін және әсердің нәтижесінде пайда болатын
қозғалыс заңдарын зерттейді. Материалдық нүкте динамикасының негізін
Ньютонның үш заңы құрайды. Динамиканың есебін шығаруды қарастырылатын
денеге әсер етуші барлық күштердің анализінен бастаған дұрыс.
Көптеген есептерде денелердің бір-бірімен үйкелісін ескеру қажет.
Үйкеліс болғанда бір дененің екінші денеге әсер етуші Q күшін екі күш
ретінде қарастырған ыңғайлы: дене бетіне нормаль бойынша бағытталған N күші
(табиғаты бойынша серпімді күш болып табылатын нормаль қысым күші немесе
тіректің реакция күші) және жанама бойынша бағытталған Ғүйк күші.

Денелердің сырғанауы кезінде Q күшінің құрауыштарының модульдері
тәжірибе жүзінде тағайындалған Кулон-Амонтонның жуықталған заңымен
байланысады:
Дене күйінің өзгеруінің себебі күш болып табылады. Табиғатта күш
болмайды. Табиғатта тек денелер мен өзара әсерлесетін өрістер болады.
Денелер мен өрістер арасындағы өзара әсерді механикада күш деп түсінеді.
Күш - сан мәні және бағытымен сипатталатын физикалық шама.
Механиканың қатты денелердің тепе-теңдікте болу шарттарын зерттейтін
бөлімін статика деп атайды. Тепе-теңдік деп дененің тыныштықта, бірқалыпты
түзусызықты қозғалыста немесе қозғалмайтын оське қатысты бірқалыпты айналып
тұрған күйін айтамыз. Дененің тыныштықта немесе бірқалыпты қозғалыста болу
шарты тікелей Ньютонның бірінші заңынан шығады, яғни денеге түсірілген
барлық қорытқы күші нөлге тең болу керек:

Статикалық процестер динамикалық процестің сызықтық және бұрыштық
үдеулері жоқ кездегі дербес жағдайы болып табылады, сондықтан статикалық
есептерді шығарудың динамикалық есептерді шығарудан айырмашылығы жоқ
дерлік.
Тепе-теңдікке қатысты есептерді жазба жасап, денеге әсер ететін барлық
күштерді бейнелеу арқылы шығару керек. Содан кейін координат системасын
таңдайды.
Әдетте оқулық есептерінде денеге әсер ететін күштер бір жазықтықта
жататын жағдай қарастырылады. Сондықтан күш моменттерін кез келген нүктеден
өтетін қозғалмайтын оське қатысты есептеуге болады.
Дененің ауырлық центрін табуға арналған есепті шығару күш моментіне
теңдеу құрудан басталады. Егер дененің ауырлық центріне модулі жағынан
ауырлық күшіне тең болатын және вертикаль жоғары бағытталған күш қоятын
болсақ, онда дене тепе- теңдік күйде болады.
Күш иіні деп - кштің әсер теу сызығынан айналыс осіне дейінгі
арақашықтықты айтамыз. Сонымен, статика есебін шешу тепе-теңдік теңдеулерін
құруға келіп тіреледі:
1. шарты кезінде кез келген үдемелі ілгерілемелі қозғалыс
болмайды;
2. шарты кезінде оның үдемелі айналмалы қозғалысы болмайды.
Статика есептерін шығарған кезде күштің түсу нүктесін, күштің әрекет ету
бағытын анықтау және осін тиімді таңдап алу аса қажет.

1. Түзусызықты жолдың бойында орналасқан А және В қалаларынан бірдей
уақытта және бір-біріне қарама-қарсы екі автокөліктер шығады. Оладың
жылдамдықтары сәйкесінше және . Қалалардың арасы L=120км
(1-сурет). Автокөліктер қанша уақыттан кейін және А қаласынан қандай
қашықтықта кездеседі? Егер әрбір автокөлік 120км өткеннен кейін
тоқтаса олардың арақашықтығы қалай өзгереді? Есепті аналатикалық
түрде және графикалық түрде шығарыңыз.
Шешуі. Есептің шартын суреттейік:

Координат басын А қаласымен сәйкестендірейік, ал ОХ осін А-дан В-ға қарай
бағыттайық. Уақытты екі көліктің де қозғалған уақытынан бастап есептейміз.
Автокөліктер тұрақты жылдамдықпен қозғалатындықтан, кез-келген уақыттағы
олардың координаталары келесі түрде анықталады:

Таңдалған санақ системасында:
, сонда
Кездесу орнында автокөліктердің координаталары өзара тең, яғни

Осы теңдеуді шешіп, кездесу уақытын анықтаймыз:

Кездесу орнын координата үшін кез-келген өрнекті пайдаланып анықтауға
болады:
мәнін мысалы бірінші өрнекке қойып, алатынымыз:

Автокөліктердің бір-бірінен қашықтығы кез-келген уақыт моментінде олардың
координаталарының айырмасының модуліне тең:

Біз есеп сұрақтарына жалпылама түрде жауап бердік. Енді сандық мәндерді
қоюға болады:

Сонымен,автокөліктер 45мин-тан кейін А қаласынан 75км жерде кездеседі.
Бұл есепті графикалық түрде шығарған ыңғайлы. Егер әр автокөліктің
координатасының уақытқа тәуелділігін графикалық түрде бейнелесек, есеп
шартында көрсетілген сұрақтардың жауабын жылдам анықтай аламыз.

I –түзуі А қаласынан шыққан автокөлік координатасының уақытқа тәуелділігін
бейнелейді. I және II түзулердің қиылысынан кездесу уақыты мен
координатасын анықтауға болады.
Суретте көрсетілгендей автокөліктер 45мин-тан кейін және А қаласынан 75км
жерде кездеседі. Графикалық түрде автокөліктер арасындағы қашықтық қалай
өзгеретінін формуласын пайдаланып көрсетуге болады.

0-t1 уақыт аралығында екі көлік те бірқалынты қозғалады. t=t1=1,2сағ
болғанда А қаласынан шыққан көлік В қаласына жетіп, тоқтайды. Ал В
қаласынан шыққан көлік қозғалысын жалғастырады. Осы уақыт моментінен бастап
олардың арақашықтығы формуласымен анықталады. t=t2=2сағ болғанда В
қаласынан шыққан көлік А қаласына келіп жетеді.

2. Кішігірім шар үйкеліссіз бірінші рет қисығы арқылы, екінші рет
қисығы арқылы қозғалып келеді.

Қисықтың және бөліктері вертикаль, ал және
бұрыштары доғал. Шардың жылдамдығының уақытқа тәуелділігін екі
жағдай үшін де график арқылы көрсету керек, егер . Шардың
нүктесіндегі жылдамдығы нолге тең.
Шешімі. Үйкеліс болмағандықтан нүктесінде шардың жылдамдығы жолға
байланыссыз сол қалпында қалады. Уақытқа тәуелді жылдамдығы сызықтармен
бейнеленеді.

және , және қисық сызықтары бірдей. 1.81-
суреттегі жолдар және қисықтарының астындағы аудандарға тең.
Жолдар бірдей болғандықтан, бұл аудардар да бірдей болады және сондықтан
екені анық. Екі жолмен де сырғитын уақыттың есебін жүргізейік:
,
болса, онда
үшін:.

Енді айырмасын табу оңай:
.

3. Дыбыс жылдамдығынан үлкен жылдамдықпен ұшатын ұшақ мс
жылдамдықпен h=4 км биіктікте Шолпан ғаламшарының үстінде ұшып
барады. Ұшақтың дыбысы планета бетіндегі ғарышкерлерге 3 с
уақыттан кейін жетеді. Шолпан атмосферасындағы дыбыс жылдамдығы
қандай?
Шешуі: 800мс

4. ОХ осінде дене бұрышпен түзусызықты қозғалып барады. ХОУ
жазықтығында дене S1=40м жол жүріп өтті. Одан кейін бұрышпен
түзусызықпен қозғала отырып S2=80м қашықтығын жүріп өтті. Қозғалысқа
кеткен толық уақыт t=4с. Жылдамдықтың орташа мәнін табу керек.
Шешуі:

мс,
мс

5. Естеліктерімді жазу кезінде, мен майшаммен түн ортасына дейін
отырдым. Ұзындықтары бірдей l екі майшамды бір уақытта жағып,
суретте көрсетілгендей қойдым. Кейін мен сол жақ қабырғадағы бірінші
майшамның көлеңкесі қозғалыссыз екенін, ал оң жақ қабырғадағы екінші
майшамның көлеңкесі жылдамдықпен қысқаратынын байқадым.

Мен бірден, бір ғана майшаммен қалатын уақытты және қараңғылықта қалатын
уақытты есептедім. Осы сұрақтарға сіздер де жауап беріп көріңіздер.
Жауабы: уақыт өткеннен кейін екінші майшам жанып бітеді, ал
уақыттан кейін біріншісі де жанып бітеді.
Шығарылуы: уақытта бірінші майшамның ұзындығы -ге, ал
екіншісінікі - -ге қысқарсын (суретті қара).

Осы уақытта оң қабырғадағы көлеңке -ге төмен түсті. Суреттің
штрихталған бөлігінде үш ұқсас ұшбұрыш бар.

Осыдан әрбір майшамның қысқару жылдамдығын анықтаймыз:

Әрбір майшамның толық жанып болу уақыты:

Яғни, - екінші майшам бірінші жанып болады.

6. Төрт тасбақа қабырғалары а болатын шаршының бұрыштарында тұр.
Тасбақалар бір уақытта және модулі бойынша тұрақты бірдей
жылдамдықпен қозғала бастайды. Бңрінші тасбақа үнемі екіншіге қарай,
екіншісі үшіншіге қарай, үшінші – төртіншіге қарай, ал төртінші
тасбақа – бірінші тасбақаға қарай қозғалады. тасбақалар қанша
уақыттан кейін кездеседі?
Жауабы:
Шығарылуы: симметрия тұрғысынан қарағанда тасбақалар кез-келген уақытта
шаршының бұрыштарында болады дейміз. Алайда бұл шаршы бұрылып, центрге
қарай жиналады.

Төрт тасбақаның кездесуі шаршы центрінде болады. Осы нүктеге жақындау
жылдамдығын ОА-ға проекциялау арқылы анықтауға болады, сонда
болғандықтан
Осы нәтижені басқа да жолмен алуға болады. Ол үшін шаршының кішірею
жылдамдығын анықтаймыз.

7. Еркін құлаған дене соңғы S=30м жолды =0,5с уақытта жүріп өтті.
Дене қандай Н биіктіктен құлады?
Жауабы: Н=200м
Шығарылуы: дене құлауының толық уақыты t. Сонда
Бұдан:
Осыдан:

8. Лифт a=2,2мс2 үдеумен көтеріле бастайды. Оның жылдамдығы
=2,4мс-ке жеткенде, лифт кабинасының төбесінен бұранда түсті.
Бұранданың құлау уақытын анықта. Лифт кабинасының биіктігі
Н=2,5м
Жауабы: =0,645с;
Шығарылуы: бұранда жерге қатысты g=9.8мс2 үдеумен және лифтке қатысты g+a
үдеумен қозғалады. оның лифтке қатысты бастапқы жылдамдығы нөлге тең.
Сондықтан құлау уақыты теңдеуінен анықталады және

9. Поезд 36кмсағ жылдамдықпен қозғалады. Егер будың берілуін
тоқтатсақ, онда поезд бір қалыпты баяу қозғала отырып, 20 сек
өткеннен кейін тоқтайды. Мыналарды: 1) поездың теріс үдеуін; 2)
аялдамаға дейін будың берілуін қандай қашықтықта тоқтату керектігін
табу керек.
Шығарылуы: Бірқалыпты айнымалы қозғалыс кезінде мынадай қозғалыстың екі
теңдеуінің болуы қажет:
(1)
(2)
Есептің шарты бойынша =0. Ендеше (2) теңдеуден мынаны аламыз:
(3)
(3) теңдеуді (1) теңдеуге қойып, мынаны табамыз:
(4)
Сан мәндерді (3) және (4) теңдеулерге қойып, мынаны аламыз:
а=-0,5мс2 және S=100м

10. Дененің жүрген жолының уақытқа тәуелділігі мына теңдеумен беріледі:
S=A-Bt+Ct2+Dt3 (А=6м; В=3мс; С=2мс2; D=1мс3). t1=1с пен t2=4с уақыт
аралығындағы : 1) орташа жылдамдықты; 2) орташа үдеуді анықта.
Шығарылуы:

Жауабы: 1) 28мс; 2) 19мс2

11. Материалдық нүкте түзу бойымен қозғалып бара жатыр. Оның үдеуі
сызықты түрде өседі және алғашқы 10 секундта 5мс2 мәніне жетеді.
Оныншы секундтың соңындағы 1)нүкте жылдамдығын; 2) нүктенің жүріп
өткен жолын анықта.
Шығарылуы:

Жауабы: 1)25мс; 2) 83,3м

12. Горизонтпен жасайтын көлбеу жазықтықта массасы m2=2кг жүк
орналасқан (а-сурет). Жүкке жеңіл шнурдың бір ұшы байланған, ал
екінші ұшына массасы m1=20кг тас байланып тұр.

Осы жүйе бірқалыпты үдемелі қозғалысқа келеді. Жүктердің үдеулерін анықта.
Жүк пен жазықтық арасындағы үйкеліс коэффициенті . Блоктың массасын
ескермеңдер.
Шығарылуы: денелердің көлбеу жазықтық бойымен қозғалысы туралы есептерде
алдымен, қозғалыстың бағытын анықтап алу қажет. Ол үшін денелерге әсер
ететін барлық күштерді бір нүктеге түсіріп, оларды жылдамдық бағытына және
оған перпендикуляр бағытта проекциялап, үдеудің бағытын анықтау қажет. Бұл
есепте тас төмен түседі, ал жүк көлбеу жазықтықпен жоғары көтеріледі.
А) Әр дененің қозғалысын жеке қарастырайық. Тасқа ауырлық күші және
шнурдың керілу күші әсер етеді. Тас үдемелі төмен түсетіндіктен:
(1)
Б) Жүкке ауырлық күші, шнурдың керілу күші, үйкеліс күші
және тіректің реакция күші әсер етеді (б-сурет).
Ох осін көлбеу жазықтық бойымен жүктің қозғалыс бағытында, ал Оу осін
көлбеу жазықтыққа перпендикуляр бағыттаймыз. Ох және Оу осьтеріне күштердің
проекциялары сәйкесінше: болады.
Түсірілген күштердің әсерінен массасы m2 жүк көлбеу жазықтық бойымен
үдемелі көтеріледі, сондықтан Ох осіне проекцияланған динамиканың негізгі
теңдеуі былай жазылады:
(2)
Көлбеу жазықтыққа перпендикуляр бағытта жүктің жылдамдағы өзгермейді,
сондықтан Ньютонның екінші заңына сәйкес:
(3)
Есептің шарты бойынша блок массасын ескермеуге болады, яғни оған тек
шнурдың екі керілу күші (Т1=Т2=Т) және тіректің реакция күші әсер
етеді (в-сурет). Ньютонның үшінші заңына сәйкес блок оське модулі бойынша
осындай, бірақ қарама-қарсы бағыттағы күшпен әсер етеді. Осы күшті анықтау
қажет.
Сыртқы күштердің әсерінен блок тепе-теңдікте тұр: оның үдеуі нолге тең. Бұл
жағдайда тепе теңдік шартын векторлық түрде көрсетуге болады. Сызбада
көрсетілгендей, параллелограм диагоналі:
Яғни, скаляр түрдегі блоктың тепе-теңдік шарты:
(4)
(1)-(4) теңдеулер жүйесінде төрт белгісіз шама бар: T, a, N, N1. Жүйені a
және N1 –ге қатысты шешіп, анықтайтынымыз:

13. Радиусы R жұқа дисктің массасы m және ол заңы бойынша
таралған, мұндағы ; r-дисктің центрінен қашықтық. -ның
қандай мәнінде диск жазықтығына перпендикуляр және оның центрі
арқылы өтетін оське қатысты дисктің инерция моменті: 1) mR23;
2)mR22 болады?

Шығарылуы: -дисктің қалыңдығы болсын. Дискті ойша радиусы r және
біртекті деп санауға болатындай өте аз қалыңдықты dr сақиналарға бөлейік.
Сонда OZ осіне қатысты әрбір сақинаның инерция моменті:

Дисктің инерция моментін дисктің массасы арқылы өрнектеу үшін, төмендегі
теңдікті пайдаланайық:

Бұл формуладан
Осыны жоғарыдағы теңдікке қойсақ,
1. бұдан =1516
2. бұдан =0, яғни бұл жағдайда диск біртекті болуы керек:

14. Массасы m материалдық нүкте t=0 уақыт моментінде F(t)=F0(1-tT)
күшінің әсерінен қозғала бастайды, мұндағы F0 – тұрақты вектор, Т-оң
константа. Табу керек: 1) қозғалыстың кинематикалық заңын; 2)
бастапқы нүктеге келу уақытын; 3) осы уақыт ішінде жүрілген жолды.
Шығарылуы. Қозғалыс теңдеуін жазайық:
(1)
ОХ осін F0 векторының бойымен бағыттайық. (1) өрнекті ОХ осіне
проекцияласақ, төмендегі дифференциалдық теңдікті аламыз:

Бастапқы шартпен . Бұдан:

Бастапқы шартты ескерсек, С=0. Яғни
(2)
Сонымен қатар . (2) өрнекті интегралдап, бастапқы шарттарды ескерсек
қозғалыстың кинематикалық заңын аламыз:

Бастапқы нүктеге қайту уақытын теңдеуінен анықтаймыз, яғни

Бұдан =3Т.
уақыт ішінде дененің жүрген жолын анықтау үшін
(3)
(3) интегралды есептеу үшін тоқтау моментін табу керек: , яғни .
Бұдан tm=2T. Сонымен,

Термодинамика
1. Поршень астындағы ыдыста күркіреуік газ бар. Осы уақытта газдың ішкі
энергиясы 80,2 кал-ға өзгерді, поршень 20 см-ге жоғары көтерілді деп
алып, күркіреуік газдың жарылған уақытындағы бөлініп шыққан газдың
мөлшерін табу керек. Поршеньнің салмағы 2кГ, ал оның көлденең
қимасының ауданы 10 см2-ге тең. Поршень үстіндегі ауа қалыпты жағдайда
тұр.
Берілгені: Шешуі:
Q=U+A
h=20см=0,2м Q=U+pV
P=2кГ=19,62Н p=FS=19.6210-3=19.62*103Па
S=10см2=10-3м2 A=pV=19.62*103*10-3*2*10-1=4Дж
Q=? Q=U+A=336Дж+4Дж=340Дж
Жауабы: Q=340Дж

2. 1*10-2м3 ауаны 2*10-3м3 көлемге дейін сығу керек. Оны қалай сығу
ыңғайлы адиабаталы ма немесе изотермалы ма?
Берілгені: Шешуі:
V1=1*10-2м3 Адиабаталық сығылудағы жұмыс:
V2=2*10-2м3
ал изотермалық сығылудағы жұмыс:

Бұдан
Біздегі V1=10-2м3, V2=2*10-2м3; =0,4. Осы берілгендерді (1) теңдеуге
қойып, аламыз - осыған қарағанда изотермалық сығу тиімді болады.

3. 400С температурада және 750 мм.сын.бағ. қысымда тұрған 28г азот 13л
көлемге дейін сығылады. Азоттың сығылудан кейінгі: 1) азот изотермалы,
2) азот адиабаталы сығылады деп алып, оның температурасы мен қысымының
қандай болатындығын табу керек. Көрсетілген әрбір жағдайдағы сығу үшін
істелінген жұмысты табыңыздар.
Берілгені:
Т1=40+273=313К
Р1=750мм.сын.бағ.=750*133Нм2=99750 Нм2
m=28г=28*10-3кг
М(N2)=28*10-3кг
V=13л=13*10-3м3
1) Т2-? Р2-? А-?
2) Т2-? Р2-? ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.