Санау жүйелері және есептерді дайындау әдістемесі


Жоспары
Кіріспе . . . 3
I. Санау жүйесі және санау жүйесінің түрлері . . . 4-8
1. 1 Сандарды бір санау жүйесінен басқа санау жүйесіне ауыстыру . . . 9-14
1. 2 Санау жүйесі ортасында арифметикалық амалдар қолдану . . . 15-18
ІІ. Есептердің әр түрлі жүйеде шығару жолдары . . . 19-20
2. 1 Арифметикалық операцияларға есептер шығару . . . 21-22
2. 2 Санау жүйесінде ауыстыру әдісінің программасын құру . . . 23-24
2. 3 «Санау жүйелері» білімді жүйелеу және қорытындылау сабақ . . . 25-29
Қорытынды . . . 30
Пайдаланылған әдебиеттер . . . 31
Кіріспе
50-ші жылдардағы математиктер мен есептеуіш машиналарын құрастырушылардың алдындағы өзекті мәселе қолданбалы бағдарламалау және жаңа есептеу құрылғыларын, шығарушылардың талаптарына сай келетін санау жүйелерін табу болды. Белсенді іздену нәтижесінде санау жүйелеріне және есептеу тәсілдеріне деген көзқарас қысқа мерзімде өзгерді.
Ежелгі интеллектуалдық шеберліктің бірі - арифметикалық санаудың біздің заманымыда да дамуы мүмкін екен.
Метематиктердің осы саласының жетістіктері және даму тарихымен танысу - мұғалім үшін маңызды, себебі қазіргі қолданылып жүрген арифметикалық санау жүйесі барлық есептеу математикасының негізі болып саналады.
Курстық жұмысымның тақырыбы «Санау жүйесі тақырыбына тапсырмалар дайындау әдістемесі». Санау жүйесі әдістерін пайдалана отырып, әртүрлі есептер шығаруға мүмкіндік бар. Санау жүйесі әдістерін қолданып, есептерді бір санау жүйесінен басқа санау жүйелеріне ауыстыруға болады. Сонымен қатар, әртүрлі жүйелердегі сандарға арифметикалық амалдар қолданып есептер шығаруға болады.
Курстық жұмысымның мақсаты қолданушыға санау жүйесі тақырыбында есептер шығару әдістері мүмкіндіктерін ашып көрсету. Осы санау жүйесі есептерінің әр түрлі әдістерін интерактивті тақтада қарастырдым.
Санау жүйесі және санау жүйесінің түрлері
Сандарды цифр деп аталатын арнайы символдардың көмегімен бейнелеу қабылданған. Сандарды атау және жазу ережелері мен әдістерінің жинағын - санау жүйесі деп аталады.
Санау жүйелері екі топқа бөлінеді: позициялық және позициялық емес.
Позициялық емес санау жүйесінде санның әрбір цифрының мәні оның алатын орнына байланысты емес. Мұндай санау жүйесінің мысалы ретінде римдік жүйені алуға болады. Бұл жүйеде жазылған XXX санына X цифры кез кез келген позицияда 10-ды (онды) білдіреді.
Позициялық емес санау жүйесінде арифметикалық амалдарды орындау едәуір күрделі болғандықтан, бүкіл дүние жүзі біртіндеп позициялық санау жүйесіне ауысты.
Позициялық санау жүйесінде цифрдің мәні оның орнына (позициясына) тәуелді. Мысалы, 737, 7 санындағы бірінші тұрған 7 жүздікті, екіншісі - 7 бірлікті, ал үшіншісі -бірліктің 7 ондық үлесін білдіреді. Кез келген позициялық санау жүйесі өзінің негізімен сипатталады.
Позициялық санау жүйесінің негізі деп онда қолданылатын цифрлар санын айтады.
Жүйенің негізі ретінде екі, үш, төрт, т. с. с кез келген натурал санды алуға болады. Демек, позициялық жүйенің сансыз көп болуы мүмкін: екілік, үштік, төрттік, т. с. с.
Негізі q санау жүйелерінің әрқайсысында сандардың жазылуы
a
 q
q
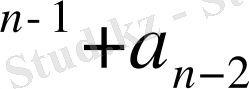 q
q
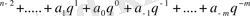
өрнегінің қысқартылған жазылуын білдіреді, мұнда a
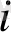 - cанау жүйесінің цифрлары; n мен m - сәйкес бүтін және бөлшек разрядтардың саны.
- cанау жүйесінің цифрлары; n мен m - сәйкес бүтін және бөлшек разрядтардың саны.
Ондық санау жүйесі
Мектеп қабырғасында сандармен жұмыс істегенде, біз бір ғана ондық санау жүйесін қолдануға дағдыландық. «Ондық» аты бұл жүйенің негізінде он негізгі жатқандығымен түсіндіріледі. Бұл жүйеде сандарды жазу үшін он цифр қолданылады - 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Адамдар ондық жүйені ыңғайлы көреді, шамасы, олар санауды алғашқыда саусақпен санап үйренгендіктерінен болар, ал аяқ пен қолдағы саусақтар саны оннан. Бірақ адамдар ондық санау жүйесін әрқашан және барлық жерде қолданбайды. Мысалы, Қытайда ұзақ уақыт бойы бестік санау жүйесін қолданған.
Ондық жүйе позициялық болып табылады, өйткені ондық санның жазылуында цифрдың мәні оның позициясына немесе сандағы орнына байланысты. Санның цифрына бөлінетін позицияны разряд деп атайды.
Мысалы, 425 санының жазуы санның 4 жүздіктен, 2 ондықтан және 5 бірліктен тұратынын білдіреді. Егер осы цифрларды басқа ретте жазатын болсақ, мысалы, 524, онда сан 5 жүздіктен, 2 ондықтан, және 4 бірліктен тұрады. Мұнда 5 цифырының саплмағы ең үлкен болады да, санның үлкен цифры деп аталады, ал 4 цифры - кіші салмақты және осы санның кіші цифры деп атайды. Егер 524 санын қосынды түрінде жазсақ,
5*10
 +2*10
+2*10
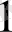 +4*10
+4*10

Осы жазбадан цифрлар салмағының айырмашылығы айқын көрінеді, бұл жазбадағы 10 саны- санау жүйесінің негізі. Санның әрбір цифры үшін, 10 негізі цифрдың сандағы орнына байланысты дәрежеленеді де, осы санға көбейтіледі. Брліктер үшін негіз1дің дәреже көрсеткіші нөлге, ондықтар үшін - бірге, жүздіктер үшін - екіге тең және т. с. с.
Егер ондық сан бөлшек болса, онда ол да қосынды түрінде оңай жазылады. Онда бөлшек бөліктің әрбір цифры үшін негіздің дәреже көрсеткіші теріс және бөлшек бөліктің үлкен цифры үшін - 1-ге, бөлшек бөліктің келесі цифры үшін - 2-ге тең және т. с. с. болады. Мысалы, келесі ондық сандар мынадай қосындымен көрсетіледі:
384, 9506=3*10
 +8*10
+8*10
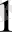 +4*10
+4*10
 +9*10
+9*10
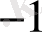 +5*10
+5*10
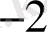 +0*10
+0*10
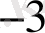 +6*10
+6*10
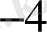
Екілік санау жүйесі.
Компьютерде, әдетте ондық емес, позициялық екілік санау жүйесі, яғни негізгі «2» санау жүйесі қолданылады.
Екілік жүйе кез келген сан 0 мен 1 цифрларының көмегімен жазылады да, екілік сан деп аталады.
Екілік санды тек 0 мен 1 цифрларынан тұратын ондық саннан ажырату үшін, екілік санның жазбасының индексіне екілік санау жүйесінің белгісі тіркеледі, мысалы, 110101, 111
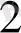
Екілік санның әрбір разрядын (цифрын) бит деп атайды.
Екілік санау жүйесінің маңызды құндылығы - цифрларды физикалық кескіндеудің ыңғайлылығы (мысалы, 1 цифрына электр кернеуінің бар болуы, ал 0 цифрына электр кернеуінің жоқ болуы сәйкес келуі мүмкін) және компьютер құрылғысының, атап айтқанда екілік сандармен арифметикалық және логикалық операцияларды орындауға арналған арифметикалық-логикалық құрылғысының қарапайымдылығы.
Ондық сандар сияқты, кез келген санды оның құрамына кіретін цифрлардың салмағының айырмашылығын анық бейнелейтін қосынды түрінде жазуға болады. Бұл қосындыда негіз ретінде 2 саны қолданылады. Мысалы, 1010101, 101 екілік саны үшін қосынды мына түрде болады.

Бұл қосынды ондық санға арналған қосынды ережесі бойынша жазылады. Берілген мысалды екілік сан жеті орынды бүтін және үш орынды бөлшек бөліктерден тұрады. Сондықтан бүтін бөліктің үлкен цифры, яғни бір 2
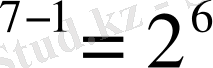 -ге көбейтіледі, бүтін бөліктің нөлге тең келесі саны 2
-ге көбейтіледі, бүтін бөліктің нөлге тең келесі саны 2
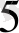 көбейтіледі және т. с. с., екінің дәрежелерінің кемуі бойынша бөлшек бөліктің кіші, 2
көбейтіледі және т. с. с., екінің дәрежелерінің кемуі бойынша бөлшек бөліктің кіші, 2
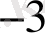 -ге көбейтілетін үшінші цифрына дейін болады. Бұл қосындыда арифметикалық операцияларды ондық жүйенің ережелері бойынша орындай отырып, 85, 625 ондық санын аламыз. Сонымен, 1010101 екілік саны 85, 625 ондық санына сәйкес немесе 1010101, 101
-ге көбейтілетін үшінші цифрына дейін болады. Бұл қосындыда арифметикалық операцияларды ондық жүйенің ережелері бойынша орындай отырып, 85, 625 ондық санын аламыз. Сонымен, 1010101 екілік саны 85, 625 ондық санына сәйкес немесе 1010101, 101
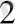 =85, 625
=85, 625
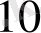 .
.
Ауыстыру ережесі. Санды екілік жүйеден ондық санау жүйесіне ауыстыру үшін, екілік санды коэффицент - цифрлармен екінің дәрежелерінің көбейтінділерінің қосындысы түрінде жазып, осы қосындыны табу керек.
Екілік жүйенің елеулі кемшілігі - санды бұл жүйеде жазу үшін 0 мен 1 цифрлары мейлінше көп қажет болатындығында. Бұл адамның екілік сандарды қабылдауын қиындатады. Мысалы, 156 ондық санының екілік жүйедегі түрі мынадай: 10011100. Сондықтан екілік жүйені, қағида бойынша компьютердің «ішкі қажеттілігі» үшін қолданады, ал адамның компьютермен жұмыс істеуі үшін, ұлкен негізді санау жүйесін таңдайды. Бұл жағдайда сегіздік және оналтылық санау жүйелері жиі қолданылады, өйткені бұдан былай көрсетілетіндей, бұл екі жүйе мен екілік жүйенің арасында сандарды бір жүйеден екінші жүйеге ауыстырудлы жеңілдететін қарапайым байланыс бар.
Сегіздік санау жүйесі
Сегіздік санау жүйесінде, яғни негізгі «8» санау жүйесінде сандар сегіз цифрдың көмегімен көрсетіледі. 0, 1, 2, 3, 4, 5, 6, 7. Мысалы, 357 санында жеті бірлік, бес сегіз және квадратталған (екі есе) үшсегіз бар, яғни 357 ═3*8²+5*8¹+7*8º, мұндағы 357 санының индексі санау жүйесін білдіреді. Жазылған қосындыда арифметикалық амалдарды ондық жүйенің ережелері бойынша орындай отырып, 357═ 239 екенін аламыз, яғни 357 сегіздік саны 239 ондық санына сәйкес.
Ондық сандарды екілік санау жүйесіне және керсінше түрлендіруді машина орындайды. Компьютерді толық пайдалану үшін машина сөздерін түсіне білу керек. Міне осы мақсатта сегіздік және оналтылық жүйелер қолданылады. Бұл жүйелердегі сандар ондық сандарға ұқсас, ал екілік жүйеге қарағанда үш (сегіздік) және төрт (он алтылық) есе аз разрядтар санын қажет етеді, өйткені 8 және 16 - екінің үшінші және төртінші дәрежелері.
Оналтылық санау жүйесі
Екілік санау жүйесі компьютерден тыс қолдануға қолайсыз екенін біз жоғарыда айтқанбыз. Мысалы, 895128 ═11011010 110011000
Екілік сандарды жазуды қысқарту үшін негізгі санау жүйесінқолданады. Бұл жүйені оналтылық деп атайды.
Оналтылық позициялық санау жүйесінде санды жазу үшін ондық санау жүйесінің цифрлары 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 және жетпейтін алты цифрды белгілеу үшін 10, 11, 12, 13, 14 және 15 ондық сандарының мәніне сәйкс латын алфавитінің алғашқы үлкен әріптері: A, B, C, D, E, F қолданылады. Сонымен ондық жүйенің барлық цифрлары және бұдан басқа алты латын әріпі оналтылық санау жүйесінің «цифрлары» болып табылады.
Оналтылық санау жүйесінің барлық цифрларын келтірейік: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Оналтылық санау жүйесінде F санынан кейін ондық жүйеде 15+1=16 дегенге сәйкес F+1 саны келеді.
Сондықтан оналтылық сан, мысалы, мына 3E5A1 түрде болуы мүмкін. Бұл санды негізі 16 екенін ескертіп, қосынды түрінде жазсақ:
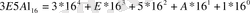 .
.
Арифметикалық операцияларды ондық жүйенің ережелері бойынша орындай отырып және А=10, Е=14 екенін ескертіп,
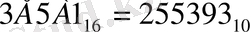 теңдігін аламыз. Ондық жүйеге қарағанда, оналтылық жүйеде сан ықшамды жазылатынына көңіл аударыңдар.
теңдігін аламыз. Ондық жүйеге қарағанда, оналтылық жүйеде сан ықшамды жазылатынына көңіл аударыңдар.
1. 1 Сандарды бір санау жүйесінен басқа санау жүйесіне ауыстыру
Сандарды бір санау жүйесінен басқа санау жүйесіне ауыстыру қажеттілігі жиі кеэдеседі. Санды екілік, сегіздік немесе оналтылық жүйелерден ондық жүйеге ауыстыру жоғарыда көрсетілген.
Бүтін ондық сандарды екілік санау жүйесіне ауыстыру
Ондық санды екілікке ауыстырғанда, бұл санды екіге бөлу керек.
Мысал. 891 санын ондық жүйеден екілік санау жүйесіне ауыстыру керек.
Шешуі:
891 2
890 445 2
1 444 222 2
1 222 111 2
0 110 55 2
1 54 27 2
1 26 13 2
1 12 6 2
1 6 3 1
0 2 1
1
(екілік санның үлкен цифры)
Соңғы бөліндіні және соңғысынан бастап барлық қалдықтарды бір жолға жазамыз. Жауабы: 891
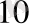 =110011
2. Ауыстыру ережесі. Бүтін оң ондық санды екілік санау жүйесіне ауыстыру үшін осы санды 2-ге бөлу керек. Алынған бөліндіні қайтадан екіге бөліп және т. с. с., алынған бөлінді 2-ден кіші болғанша бөле беру керек. Нәтижесіне соңғы бөлінді мен соңғысынан бастап барлық қалдықтарды бір жолға жазу керек.
=110011
2. Ауыстыру ережесі. Бүтін оң ондық санды екілік санау жүйесіне ауыстыру үшін осы санды 2-ге бөлу керек. Алынған бөліндіні қайтадан екіге бөліп және т. с. с., алынған бөлінді 2-ден кіші болғанша бөле беру керек. Нәтижесіне соңғы бөлінді мен соңғысынан бастап барлық қалдықтарды бір жолға жазу керек.
Мысал: 35 10 х 2
35 2
34 17 2
1 16 8 2
1 8 4 2 Жауабы: 100011 2.
0 4 2 2
0 2 1
0
Тексеру: 100011 2 =1*2 5 +0*2 4 +0*2 3 +0*2 2 +1*2 1 +1*2 0 = 32+2+1=35 10
Ондық бөлшектерді екілік санау жүйесіне ауыстыру.
Ондық бөлшектерді екілік санау жүйесіне ауыстыру оны екіге көбейтіп, бүтін бөліктерді табудан тұрады.
Мысал: 0, 625 ондық бөлшегін екілік санау жүйесіне ауыстырайық.
Екілік бөлшектің үтірден кейінгі бірінші цифрын табу үшін берілген санды 2-ге көбейтіп, көбейтіндінің бүтін бөлігін ерекшелеу керек.
Шешуі:
0, 625*2 = 1, 250, бүтін бөлігі 1-ге тең;
0, 250*2 =0, 500, бүтін бөлігі 0-ге тең;
0, 500*2 = 1, 000, бүті бөлігі 1-ге тең.
Соңғы көбейтіндінің бөлшек бөлігі нөлге тең. Ауыстыру аяқталды. Алынған бүтін бөліктің мәнін бірінші цифрдан бастап бір жолға жазамыз. Жауабы: 0, 625
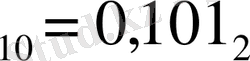 .
.
2-ге көбейткенде әрқашанда ондық санның тек бөлшек бөлігі ғана қатысады.
Ауыстыру ережесі. Ондық оң бөлшекті екілік санау жүйесіне ауыстыру үшін бөлшекті 2-ге көбейту керек. Көбейтіндінің бүтін бөлігін екілік бөлшектің үтірден кейінгі бірінші цифры ретінде алып, бөлшек бөлігін қайтадан 2-ге көбейту керек. Енді бұл көбейтіндінің бүтін бөлігін екілік бөлшектің келесі цифры ретінде алып, бөлшек бөлігін тағы 2-ге көбейту керек және т. с. с.
Ақырғы ондық бөлшекті екілік жүйеге ауыстыру кезінде периодты бөлшек алынуы мүмкін.
Мысал: 0, 3 ондық бөлшегін екілік санау жүйесінде ауыстырайық.
Шешуі:
0, 3*2= 0, 6, бүтін бөлігі 0-ге тең;
0, 6*2=1, 2, бүтін бөлігі 1-ге тең;
0, 2*2=0, 4, бүтін бөлігі 0-ге тең;
0, 4*2 =0, 8, бүтін бөлігі 0-ге тең;
0, 8*2=1, 6, бүтін бөлігі 1-ге тең;
0, 6*2=1, 2, бүтін бөлігі 1-ге тең және т. с. с.
0, 6-ның бөлшек бөлігі, есептеудің екінші қадамнда болған.
Сондықтан есептеулер қайталана бастайды. Демек, 0, 3 саны екілік санау жүйесінде периодты бөлшек түрінде көрсетіледі.
Жауабы: 0, 3
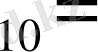 0, 0(1001)
0, 0(1001)
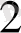 .
.
Іс жүзінде бұл операцияларды үтірден кейін цифрлардың берілген саны алынғанша жалғастырады.
Ондық сандарды сегіздік санау жүйесіне ауыстыру.
Сандарды одық жүйеден сегіздік жүйеге ауыстыру үшін екілік жүйеге ауыстыру әдісін қолдануға болады.
Түрлендіретін санды ондық жүйенің ережесі бойынша, 7-ден аспайтын қалдығын еске сақтай отырып, 8-ге бөледі. Егер алынған бөлінді 7-ден үлкен болса, онда оны да қалдықты еске сақтай отырып, 8-ге бөледі. Жаңа бөліндіні, егер ол 0-ден көп болса, өз кезегінде 8-ге бөледі. Бұл 8-ге бөлу процесі алынған бөлінді 0-ге тең болғанша жалғаса береді. Содан кейін, соңғысынан бастап барлық қалдықтарды қатар жазып алу керек.
Мысал: 892 санын ондық жүйеден сегіздік санау жүйесіне ауыстырайық.
Шешуі:
892 8
888 111 8
3 104 13 8
7 8 1 (екілік санның үлкен цифры)
5
Жауабы: 891
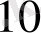 = 1573
= 1573
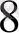 .
.
Ондық сандарды оналтылық санау жүйесіне ауыстыру.
Ондық сандарды оналтылық жүйеге жоғарыдағыға ұқсас ауыстырады. Айырмашылығы - берілген сан сегіздің орнына 16 - ға бөлінеді.
Мысал. 893 санын ондық жүйеден оналтылық санау жүйесіне ауыстырайық.
Шешуі:
893 16
882 55 16
11 48 3
7 (екілік санның үлкен цифры)
Сандарды екілік жүйеден сегіздік санау жүйесіне ауыстыру.
Екілік санды сегіздік немесе оналтылық санға түрлендіру процесі өте қарапайым.
Сегіздік санның кез келген цифрын жазу үшін екілік цифр қажет. Сондықтан түрлендіретін екілік санды оңнан солға қарай үш-үштен екілік цифрлар тобына бөледі, мұнда ең сол жақтағы топта екілік цифрлар үштен кем болуы мүмкін. Мысалы, 011 екілік цифры сегіздік санау жүйесінде үш цифры болып табылады. Сонан кейін екілік цифрлардың әрбір тобын кестеде көрсетілген сегіздік цифр түрінде жазылады.
Мысалы, үш екілік цифрдан тұратын топтарға бөлінген 110011 екілік санын 1 101 111 011 сияқты жазып алып және әрбір топты бір сегіздік цифрмен ауыстырып жазғаннан кейін, 1573 сегіздік санын алуға болады.
Санды екілік жүйеден сегіздік немесе оналтылық жүйеге көшіру үшін сол санды оңға және солға қарай триадаларға (сегіздік) немесе тетрадаларға (он алтылық) бөліп, әрбір топты соған сәйкес сегіздік (он алтылық) цифрмен алмастыру керек.
Мысалы: 10101001, 10111
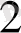 =10 101 001, 101 110
=10 101 001, 101 110
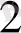 =251. 56
=251. 56
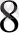
2 5 1 5 6
Сандарды екілік жүйеден оналтылық санау жүйесіне ауыстыру
Екілік санды оналтылық санау жүйесіне жоғарыдағыға ұқсас түрлендіреді: әрбір түрлендіретін екілік сан оңнан солға қарай әрқайсысында төрттен екілік сан бар топтарға бөлінеді, өйткені оналтылық санның кез келген цифрын жазу үшін төрт екілік цифр қажет.
Сондықтан алдыңғы мысалда қолданылған 110011 екілік санды төрт екілік цифрлардан тұратын топтарға бөлгеннен кейін, 11 0111 1011 сияқты жазып және әр топты оналтылық цифрмен ауыстырғаннан кейін, 37В оналтылық санын алуға болады. Мысалы,
1011
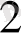 =1*2
=1*2
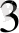 +0*2
+0*2
 +1*2
+1*2
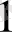 +1*2
+1*2
 =11
=11
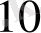 = B
= B
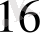 .
.
Санды екілік жүйеден оналтылық жүйеге көшіру үшін сол санды оңға және солға қарай тетрадаларға (он алтылық) бөліп, әрбір топты соған сәйкес он алтылық цифрмен алмастыру керек.
Мысалы:
10101001, 10111
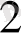 = 1010 1001, 1011 1000 = А9, В8
= 1010 1001, 1011 1000 = А9, В8
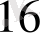
А 9 В 8
Сандарды сегіздік және оналтылық санау жүйелерінен екілік жүйеге ауыстыру.
Сегіздік немесе оналтылық санды екілік санға түрлендіру бастапқы санның әрбір цифрын үш (сегіздік сан үшін - триадаларға) немесе төрт (оналтылық сандар сандар үшін - тетрадаларға) екілік сандардан тұратын топтарға жай ғана ауыстыру арқылы жүзеге асырылады.
Мысалы: 123
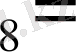 001 010 011 = 1010011
001 010 011 = 1010011
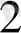
A17
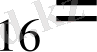 1010 0001 0111 = 101111
1010 0001 0111 = 101111
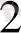 .
.
Егер ауыстырғаннан кейін екілік санның бүтін бөлігі нөлдерден басталса, онда олар алып тасталады, Бөлшек бөліктің соңындағы нөлдермен де тура солай жасайды.
Мысалдар:
253, А4
001001010011. 10100100
Equation. 3 = 1001010011, 101001
.
537, 1
= 101 011 111, 001
;
5 3 7 1
1. 2 Санау жүйесі ортасында арифметикалық амалдар қолдану
Екілік санау жүйесінде арифметикалық амалдар ондық жүйедегі ережелер бойынша орындалады, айырмашылығы - санау жүйесінің негізі екіге тең және тек екі цифр ғана пайдаланылады.
Қосу
Қосу операциясын қарастырайық. Екілік сандарды қосу сәйкес разрядтардың цифрларын тасмалды есепке алып қосуға саяды.
Екі екілік санды қосқанда, келесі төрт ереже қолданылады.
0+0=0
1+0=1
0+1=1
1+1=10 бір көрші (үлкен) разрядқа тасмалданады.
Мысал. Екі екілік 101 + 11 сандарын қосуды (ондық жүйеде бұл: 5+3 = 8) орындайық.
Жетпеген нөлдерді қосып, қосу амалын бағанда орындаған жөн
101
+
011
Қосу процесін кезеңімен қарастырайыық.
- Алдымен қосу кіші разрядта орындалады:
1 + 1= 10. Қосындының кіші разрядына 0 жазылады да, бірлік алдыңғы үлкен разрядқа тасымалданады.
2. Келесі сол жақ разрядтың цифрлары мен тасымалдың бірлігі қосылады: 0+1+1= 10. Қосындының бұл разрядына 0 жазылады да, бірлік тағы да келесі үлкен разрядқа тасымалданады.
3. Енді үшінші сол жақ разрядтың цифрлары мен тасымалдың бірлігі қосылады: 1+0+1 = 10. Бұл разрядта 1 жазылады, ал бірлік келесі үлкен разрядқа тасымалданады, т. с. с.
4. Нәтижеде
101
+
011
1000 алдық.
Сонымен, 1000
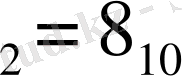 .
.
Осы ережелерді қолдана отырып, келесі екілік сандарды қосып және жауабын тексеріп көрейік
10111 0111
+ +
10110 0111
101101 1110
Қосу - екілік арифметикадағы маңызды операция. Компьютерде екілік сандармен орындалатын басқа үш арифметикалық операция - азайту, көбейту, бөлу, әдетте қосудың көмегімен орындалады.
Мысалдар:
1110 10001 1010
+ +1110 +10001 +0101
11101 11101 100010
Азайту
Екілік сандарды азайту кезінде мыналарды есте сақтау керек:
0- 0 =0
1 - 0= 1
0 - 1 =1 көрші (үлкен) разрядтан бірді қарызға аламыз.
1 - 1 = 0
Мысал. Екілік сандардың 1010 - 101 айырымын табайық. Азайтуды кіші разрядтан бастап бағанда орындайық:
1010
-
101
Азайту процесін кезеңмен қарастырайық:
- Кіші разрядта: 0-1. Сондықтан үлкен разрядтан бірлікті қарызға аламыз да, 10-1=1-ді табамыз.
- Келесі разрядта 0-0=0 болады.
- Сол жақтағы разрядта тағы да: 0-1. Үлкен разрядтан 1-ді қарызға алып, 10-1=1-ді табамыз.
- Келесі разрядта 0 қалады.
- Нәтижеде
1010
-
101 алдық.
Енді осы ережелерді қолдана отырып, екілік сандарды азайтуды орындаңдар да, жауабын салыстырып тексеріңдер:
10111 1110
-
10110 0101
- 1001
Мысалдар:
1101 1011 1110 1001
-1 -110 -111 -011 -1010
0 111 100 1011 -0001
Көбейту
Екілік сандарды көбейткенде мыналарды есте сақтау керек:
Мысал. 101
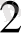 мен 110
мен 110
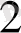 екілік сандарының көбейтіндісін табыңдар. Сандарды көбейтуді кіші разрядтан бастап бағанда орындайық:
екілік сандарының көбейтіндісін табыңдар. Сандарды көбейтуді кіші разрядтан бастап бағанда орындайық:
101
* Тексеру: 101
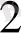 = 1*2
= 1*2
 +0*2
+0*2
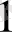 +1*2
+1*2
 =5
=5
110 110
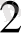 =1*2
=1*2
 +1*2
+1*2
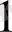 +0*2
+0*2
 =6
=6
000
101
+
101
0
0
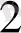 =1*2
=1*2
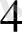 +1*2
+1*2
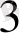 +1*2
+1*2
 +1*2
+1*2
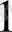 +0*2
+0*2
 =16+8+4+2+0=30
=16+8+4+2+0=30
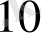 ,
,
Яғни 5*6=30
Көбейту процесін кезеңмен қарастырайық:
- Кіші разрядқакөбейте отырып, кесте бойынша 000 аламыз.
- Келесі разрядқа көбейткенде, бір разряд солға жылжыған 101-ді аламыз.
- Үлкен разрядқа көбейткенде де, тағы бір разряд солға жылжыған 101-ді аламыз.
- Енді екілік сандарды қосу кестесін есепке ала отырып, қосамыз да, 0нәтижені аламыз.
Екілік жүйедегі көбейту кестесі тым қарапайым болғандықтан, көбейту тек көбейгішті жылжыту мен қосудан тұрады.
Бөлу
Екілік санау жүйесінде бөлу - ондық жүйедегі сатылап бөлу сияқты орындалады. Екілік жүйеде бөлу мейілінше оңай орындалады, өйткені бөліндінің кезекті цифры тек нөл немесе бірлік қана болады.
30 2
30 15 2
0 14 7 2
1 6 3 2
1 2 1
1
Мысал.
30 санын 5 санына бөлейік. Ол үшін 30
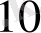 санын екілік 0
санын екілік 0
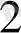 -ге ауыстырайық.
-ге ауыстырайық.
5
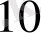 = 101
= 101
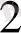 - ге сатылап бөлуді орындайық.
- ге сатылап бөлуді орындайық.
0 101
-101 11
101
- 110= 6нәтижесін алдық.
ІІ. Есептердің әр түрлі жүйеде шығару жолдары
Есеп 1. 124 санын ондық жүйеден екілік санау жүйесіне ауыстыру керек.
124 10 х 2
124 2
124 62 2
0 62 31 2
0 30 15 2
1 14 7 2
1 6 3 2 Жауабы:
1 2 1 00 2
1
Тексеру:
00 2 =1*2 6 +1*2 5 +1*2 4 +1*2 3 +1*2 2 +0*2 1 + 0*2 0 =64+32+16+8+4=124 10
Есеп 2. 27 санын ондық жүйеден екілік санау жүйесіне ауыстыру керек.
27 10 х 2
27 2
26 13 2
1 12 6 2
1 6 3 2
0 2 1 Жауабы:
1 11011 2
Тексеру:
11011 2 =1*2 4 +1*2 3 +0*2 2 +1*2 1 +1*2 0 = 16+8+2+1=27 10
Есеп 3.
1A3, F
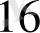 санау жүйесін екілік санау жүйесіне ауыстыру.
санау жүйесін екілік санау жүйесіне ауыстыру.
1A3, F
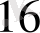 = 1 1010 0011,
= 1 1010 0011,
1 A 3 F
Есеп 4. 75 ондық санау жүйесін оналтылық санау жүйесіне аудару.
75 10 x 16
75 16
64 4
11
Тексеру: 411 16 =11*16 0 +4*16 1 =11+64=75 10 411 16 =4В 16
Есеп 5. 108 ондық санау жүйесін сегіздік санау жүйесіне аудару.
108 10 х 8
108 8
104 13 8
4 8 1 Жауабы:
5 154 8
Тексеру:
154 8 =4*8 0 +5*8 1 +1*8 2 =4+40+64=108 10
Есеп 6. 75 ондық санау жүйесін сегіздік санау жүйесіне аудару.
75 10 x 8
75 8
72 9 8
3 8 1
1 Тексеру: 113 8 =3*8 0 +1*8 1 + 1*8 2 =3+8+64=75 10
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz