Математикалық модель түсінігі

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 22 бет
Таңдаулыға:

Мазмұны

Кіріспе

І бөлім . Ауылшаруашылық есептерді жоспарлау.

Ауылшаруашылық өндірісін есепке алу . . . 5
Ауылшаруашылығын орналастырудағы материалдарды тиімді пішу туралы есеп . . . 10
Тапсырманы кәсіпорындарға бөлу туралы есеп . . . 11

ІІ бөлім . Ауылшаруашылық есептерді жоспарлау модельдері.

2. 1. Математикалық модель түсінігі . . . 16

2. 2. Жоспарлаудағы математикалық модельдің құрылымы . . . 18

2. 3. Математикалық моделдің иерархиясы және оны ұсынудың түрлері . . . 20

Қорытынды . . . 26

Пайдаланылған әдебиеттер . . . 27

Кіріспе

Қазіргі таңда, еліміздің нарық қатынасына көш отырған кезеңінде, экономика ғылымдарының, ауылшаруашылығына байланысы барлық салалардағы жоспарлау және басқарудың, сондай-ақ еліміздің әлеуметтік-экономикалық жақтан жедел дамуының негізгі жолдарының бірі-математикалық оптимизациялау және математикалық моделдеу әдістерін, электронды есептеуіш машиналарын (ЭЕМ) және дербес компьютерді кеңінен қолдану болып табылады. Математикалық оптимизациялау және математикалық моделдеу әдістерін, ЭЕМ, дербес компьютерді күнделікті жұмыста қолдана білу, қолда бар ресурстарды нәтижелі пайдалану үшін ең тиімді жоспарды таңдауға, өте аз шығынмен өндірістің дамуына пайдалы жоспарды құруға, өндіріс күштерінің дұрыс орналасу проценттерін жасауға, сондай-ақ экономикалық есептеулердің орындалу уақытын қысқартуға және басқарудың өнімділігін арттыруға қолайлы жағдайлар туғызады.

Өндіріс ауқымының көбеюі, мамандандырудың тереңдеуі, конерцияның дамуы, шаруашылық аралық байланыстардың күрделенуі және экономикадағы сандық және сапалық өзгерістер басқарудың көптеген әдістерінің арасынан ең тиімдісін таңдап алуды қажет етеді.

Ауылшаруашылығын басқару мен жоспарлау моделдері мәселесін тиімді етуде маманнан тек қана әртүрлі өндірістік жағдайларда экономикалық талдау жасай білу өнері ғана емес сондай-ақ оған тән математикалық моделді құра білу. өзіне сай териндермен түсінік бере білуді де қатаң талап беріп отыр. Экономикалық мәселлерге математикалық талдау жасау математикалық және терең экономикалық есептердің дұрыс математикалық қойылымын оптимизациялық және математикалық моделдеу әдістерін толық меңгерген маман ғана шешуі мүмкін.

Сонымен, болашақта ауылшаруашылық өндіріс тиімділігін арттыру мәселесін шешудің негізгі жолдарының бірі ғылымның соңғы жетістіктерін, оптимизациялау математикалық моделдеу әдістерін және ЭЕМ мен дербес компьютерді қолдану болып табылады.

Математикалық әдістерді экономикалық зерттеулерде тәжірбие жүзінде қолдану 1951 жылдан басталды, ал 1955 жылдан бастап кеңінен қолданылатын болды.

Математиканың экономикаға енуі жоспарлау мен басқарудың қазіргі кездегі ғылыми-техникалы революциясының аса маңызды ерекшелігі болып табылады. Бұл процесс соңғы 30 жылда бүкіл әлемде қарцынды түрде жүргізілуде. Математикасын әдіс мектептерінің АҚШ, Франция, Германия, Англияда ашылуының обьективті себептері мол. ЭЕМ, оптимизациялау және математикалық моделдеу әдістерінің дамуы мен жылдам таралуы бұл әдістердің қолдану ауқымының кеңеюіне және басқарудың автоаттандырылған жүйелерінің құрылуына тікелей әсер еткені белгілі.

Қазіргі таңда ауылшаруашылық өндірісті басқару мен жоспарлауда оптимизациялау және математикалық моделдеу әдістерімен ЭЕМ қолдану жоспарлы-эконмикалық есептеулердің дәлдігін арттыруға, жасалынған жоспарлардың ғылыми деңгейін көтеруге, өндіріс тиімділігін арттыруға мүмкіндік береді.

Оптимизациялық және математикалық моделдеу әдістері өзінің жоғары нәтижелігіне қарамай бүгінгі күнде өндірісті басқару және жоспарлауда іс-тәжербиесіне баяу енгізіліп отыр мұның бірден-бір себебі жоғары білімді мамандардан жетіспеуі.

Бүгін таңда өз жұмысында оптимизациялау және математикалық моделдеу әдістері мен ЭЕМ, дербес компьютерді кеңінен қолдана білетін жоғары білікті мамандар дайындау кезек күттірмейтін мәселе болып отыр.

Бұл жұмысының негізгі мақсаты әр түрлі салалардағы жоспарлау, басқару ұйымдастыру мәселелерін шешуде ЭЕМ және оптимизациялау, математикалық моделдеу әдістерін қолданатын болашақ мамандарды құруға олардыңтиімді қолданылатын салаларын анықтауға өндірісті басқаруға даярлайтын математикалық әдістер мен моделдердің негізгі топтарын және оларды тиімді әдістерімен шешу жолдары оқып үйрету мәселелері қарастырылылады.

І-тарау . Ауылшаруашылық есептерді жоспарлау.

1. 1. Ауылшаруашылық өндірісін есепке алу

Іс-тәжірбиеде кең тараған есептер тобының бірі шектеулі өндіріс қорларын ұтымды пайдаланып, максималды өнім өндіруді жоспарлау. Бұл есептің мәні мынада.

Кәсіпорын әр-түрлі өнім шығарады делік. Шығарылатын өнімдердің түрлерін шартты түрде a ₁ a ₂ . . . a _n деп белгілейік. Осы өнімдерді өндіру үшін кәсіпорын әр-түрлі шикізат қорын пайдаланады. Пайдаланылатын шикізат қорларының түрлерін шартты түрде b ₁ b ₂ . . . b _м деп белгілейік. Төмендегі белгілеулерді енгізейік: a _ij (i=1, m; j=1, 4) - j-өнімнің бір данасы өндіруге жұмсалатын і-шикізат мөлшері.

b _і (і= 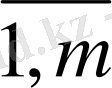) - кәсіпорын қоймасындағы і-шикізат қорының мөлшері c _j (j= 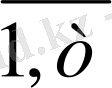) - дайын j-өнімнің бір данасынан сатудан түседін пайда;

Әдетте есептің берілгенін төмендегі 1. 1 кесте түрінде береді.

Шикізат түрлері

а ₁

Дара өнімге шаққандағы жұмсалынған шикізат мөлшері

а ₂ a _n

Шикізат қорының көлемі

Шикізат түрлері: В ₁

а1: а ₂

Дара өнімге шаққандағы жұмсалынған шикізат мөлшеріа2an: а ₂ a _1n

Шикізат қорының көлемі: b ₁

Шикізат түрлері: В ₂

а1: а ₂₁

Дара өнімге шаққандағы жұмсалынған шикізат мөлшеріа2an: а ₂₂ a _2n

Шикізат қорының көлемі: b ₂

Шикізат түрлері:

а1:

Дара өнімге шаққандағы жұмсалынған шикізат мөлшеріа2an:

Шикізат қорының көлемі:

Шикізат түрлері: Вm

а1: а _m1

Дара өнімге шаққандағы жұмсалынған шикізат мөлшеріа2an: а _m2 a _mn

Шикізат қорының көлемі: b _m

Шикізат түрлері: Пайдасы

а1: с ₁

Дара өнімге шаққандағы жұмсалынған шикізат мөлшеріа2an: c ₂ c _n

Шикізат қорының көлемі:

Қолда бар шикізат мөлшерін ұтымды пайдалана отырып, сатылғаннан соң максималды пайда түсіретін өнім өндіру жоспарын құру керек.

Шешуі: Ізделінді өндірілетін өнімдер шамасын xj (j= 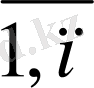) деп белгілейік. Сонда барлық өндірілген өнім түрлерін сатудан түсетін пайданың жалпы көлемі мына өрнекпен есептелінеді:

F(x) = c ₁ x ₁ +c ₂ x ₂ + . . . +c _n x _n = 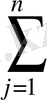c _j x _j

Есептің шарты бойынша өнім өндіруге кететін шикізат шығыны қолда бар шикізат мөлшерінен аспауы тиіс:

a ₁₁ x ₁ +a ₁₂ x _{2+ . . . +} a _n x _n ≤b ₁

a ₂₁ x ₁ +a ₂₂ x ₂ + . . . +a _2n x _n ≤b ₂

- - - - - - - - - - -

a _m1 x ₁ +a _m2 x ₂ + . . . +a _mn x _n ≤b _m

Ізделінді мәндердің экономикалық мағынасы болу үшін олар теріс сан болмауға тиісті, басқаша айтқанда өндірілетін өнім мөлшері теріс мән қабылдай алмайды. Егер, қайсыбір айнымалының мәні нөлге тең болса, онда бұл өнімді өндіру өндіріс үшін экономикалық тұрғыдан тиімді емес деген мағына береді. Сондықтан, кез келген есептің негізгі талаптарының бірі-айнымалылардың мәні теріс сан болмауға тиісті:

v _j . x _j =0, (j= )

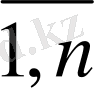Есепті шығарудағы негізгі мақсат - өнімдерді сату барысында ең көп пайда табу болғандықтан F функциясы шах-ға зерттелінеді.

Сонымен, өндірісті жоспарлау есебінің математикалық моделін төмендегіше жазуға болады:

F(x) = 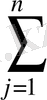c _j x _j →mах (1. 1)

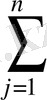a _ij x _j ≤b _i (i= 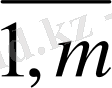) (1. 2)

x _j ≥0 (j= 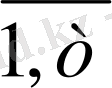) (1. 3)

түріндегі сызықтық Ғ функциясы деп аталады.
Түріндегі шарттар шектеулер жүйесі деп аталады
Түріндегі шарттар айнымалылардың теріс еместік шарты

Математикалық тұрғыдан бұл есепті былайша тұжырымдауға болады: Берілген (1. 1) мақсат функциясына максимум мен әперетін және (1. 2), (1. 3) теңсіздіктер жүйесін қанағаттандыратын x=(x ₁ x ₂ . . . x _n ) векторын табу қажет. Берілген есептің мақсат функциясымен шектеулер жүйесі сызықтық болғандықтан бұл есеп сызықтық бағдарламалау есеп-н жатады. (1. 2) Азық құрамы (Рацион) туралы есеп.

Күнделікті шаруашылықта жиі кездесетін технологиялық есептердің бір түрі дұрыс рацион дайындау есебі болып табылады. Енді осы есептің ауыл шаруашылығында кездесетін бір түрін қарастырайық.

Мәселен, малды дұрыс семірту үшін оларға күнделікті рацион жем-шөптің n түрінен дайындалады, ал күнделікті рационға қажетті нәрлі заттардың түрі m -ге делік. Төмендегі белгілеулерді енгізейік:

a _ij - жем - шөптің j- түрінің құрамындағы нәрлі i-заттың мөлшері;

b _i -нәрлі і - заттың қажет мөлшері;

c _j (j= 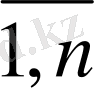) - жем - шөптің j-түрінің дара мөлшерінің бағасы. Әдетте есептің берілгенін төмендегі 1. 2 кесте түрінде береді.

1. 2. кесте

Нәрлі заттар аты

Жем-шөптің 1 кг - дағы нәрлі заттың

мөлшері

а ₁ а ₂ а _n

Нәрлі заттың қажет мөлшері

В ₁

а ₁₁ а ₁₂ а _1n

b ₁

В ₂

а ₂₁ а ₂₂ а _2n

b ₂

В _m

а _{m 1} а _mn

b _m

жем-шөптің 1 кг-ның бағасы

с ₁ с ₂ с _n

Рационда ондағы пайдалы, қоректік, нәрлі заттардың әрқайсысы b _і -дан кем мөлшерде болмауға тиіс.

Осындай шарттарды қанағаттандыратын және өзіндік жалпы құны ең арзан болатын рационға енетін азық құрамын жасау керек.

Шешуі : Ол үшін азық құрамына енетін азық-түлік түрлерінің мөлшерін x _j (j= 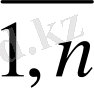) деп белгілейік. Сонда жалпы жұмсалынатын қаржы келесі формуламен анықталады.

F(x) =c ₁ +x ₁ +c ₂ +x ₂ + . . . +c _n x _n = 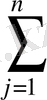c _j x _j →min

есептің шарты бойынша азық құрамындағы пайдалы заттар көрсетілген мөлшерден кем болмауы тиіс:

a ₁₁ x ₁ +a ₁₂ x ₂ + . . . +a _1n x _n ≥b _1,

a ₂₁ x ₁ +a ₂₁ x ₂ + . . . +a _2n x _n ≥b ₂ ,

─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─

a _m1 x ₁ +a _m2 x ₂ + . . . +a _mn x _n ≥b _m,

ал азық-түлік мөлшері теріс мән қабылдай алмайды:

x _j ≥0(j= )

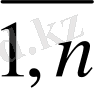Сонымен, қарастырылып отырған рацион есебінің математикалық моделін қосынды белгісін пайдаланып төмендегіше жазуға болады:

F(x) = 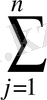c _i x _j →min (1. 4)

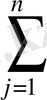a _ij x _j ≥b _i (i= 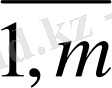) (1. 5)

x _j ≥0 (j= 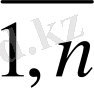) (1. 6)

Математикалық тұрғыдан бұл есепті былайша тұжырымдауға болады:

Берілген (1, 4) мақсат функциясына минимум мән әперетін және (1, 5) (1, 6) теңсіздіктер жүйесін қанағаттандыратын x= (х ₁ , х ₂ , . . . х _n ) векторын табу қажет. Берілген есептің мақсат функциясы мен шектеулер жүйесі сызықтық болғандықтан, бұл есепте сызықтық бағдарламалау есебіне жатады.

Жоғарыда қарастырған (1. 1) -(1. 3), (1. 4) -(1. 6) есептерін матрица түрінде де жазуға болады. Ол үшін төмендегі белгілеулерді енгізейік:

a ₁₁ a ₁₂ . . . a _1n - шектеуші шарттардағы белгісіздер

A= a ₂₁ a ₂₂ . . . a _2n коэффиценттерінен құралған матрица;

- - - -

a _m1 a _m2 . . . a _mn

c=(с ₁ , с ₂ , . . . , с _n ) - мақсат функциясындағы белгісіздер

коэффициенттерінен құралған матрица - қатар;

x ₁

Х= x ₂ - белгісіздерден құралған матрица - баған

. . .

x _n

b ₁ - шектеуші шарттар оң бөлігінен құралған матрица - баған

b ₂

B= . . .

b _n

Сонда (1. 1) -(1. 3) есебінің матрицалық түрде жазылуы төмедегідей болады:

F(x) =c _* x→ max (1. 7)

A _* X≤B, (1. 8)

x≥0 (1. 9)

Ал (1, 4) -(1, 6) есебінің матрицалық түрде жазылуы төмендегідей болады:

F(x) =c _* x→min (1. 10)

A _* X≥B (1. 11)

x≥0 (1. 12)

Сызықтық бағдармалау есептерінде шектеуші шарттар теңдік түрінде де берілуі мүмкін, ал мақсат функциясы максимумға немесе минимумға зерттелнеді. Мұндай есептердің матрицалық түрде жазылуы төмендегідей болады:

F(x) =c _* x →extr, (1. 13)

AX=B, (1. 14)

x≥0 (1. 15)

1. 2. Ауылшаруашылығын орналастырудағы материалдарды тиімді пішу туралы есеп

Белгілі бір бұйымды шығару үшін әрқайсында көлемі b _j -ге тең n партия материал бар делік. Әрбір бұйымды жасау үшін осы материалдардан s түрлі бөлшек дайындалу саны р _к болуы керек. Ол бөлшектерді пішудің (дайындаудың) т түрлі тәсілі бар; егер і-партияның материал бірлігін j тәсілмен пішетін болса, онда а _ijk дана к-бөлшек алуға болады. Қолда бар материалдардан дайындалатын бұйым саны ең көп болатын пішу жоспарын табу керек.

Шешуі: белгілеу енгізейік: x _ij -i партия материалдарының j - тәсіл бойынша пішілетін көлемі делік.

Сонда і-партия материалдарының j тәсілімен пішкенде алынатын к-бөлшек саны: a _ijk* x _ij ,

ал і-партия материалдарын барлық тәсілмен пішкенде алынатын

k-бөлшек саны:

a _{ijk *} x _ij

Сонымен, барлық п партиядағы материалдарды барлық m тәсілмен пішу кезінде дайын болатын к-бөлшек саны:

F _k = 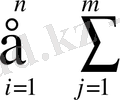a _{ijk *} x _ij , (K=1, s) (1. 16)

Бір бұйым үшін қажетті К-бөлшек саны Р _к болғандықтан, дайын бұйым саны келесідей болуға тиіс:

F= min 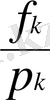Equation. 3, k= 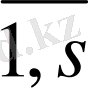(1. 17)

немесе, (1. 16) формуласы бойынша:

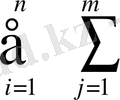a _ijk* x _ij

F=min, k= 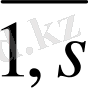(1. 18)

P _k

Әрбір партиядан жұмсалынатын материал саны белгілі, сондықтан :

x _i1 +x _i2 + . . . +x _im =b _i , i= 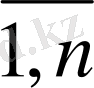(1. 19)

Сонымен бірге: x _ij ≥0 (1. 20)

Сонымен бұл есептің математикалық моделін былайша тұжырамдауға болады: Берілген (1, 18) мақсат функциясына максимум мән әперетін және (1, 19) -(1, 20) шарттарын қанағаттандыратын х _ij -дің мәндерін табу керек. Бұл есепті кейде «максимин» есебі деп те атайды .

1. 3 Тапсырманы кәсіпорындарға бөлу туралы есеп.

Өндіріс саласының жоспары бойынша белгілі бір Т уақытта А _i бұйымынан N _i дана (i = 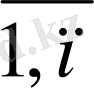) шығарылуға тиіс . Бұл бұйымдар m кәсіп орында шығарылады, бірақ ешбір кәсіпорын бірмезгілде бірнеше түрлі бұйымды қатарынан шығара алмайды. Сонымен бірге a _ij -j кәсіпорында уақыт бірлігінде шығаратын. А _і бұйымның сан мөлшері, яғни a _ij әрбір кәсіпорынның еңбек өнімділігі. Ал b _ij -осы кәсіпорында шығарылған А _і бұйымның бір данасын а кеткен шығын. Шығарылатын барлық өнімге кететін шығын ең аз болатындай етіп тапсырманы кәсіпорындарға бөлу жоспарын жасау керек.

Шешуі: берілген есептің математикалық моделін түзу үшін х _іj деп А _і бұйымын шығаруға жұмсалатын j кәсіпорынның уақытын белгілейік. Сонда өндіріс кәсіпорындарының шығарылатын барлық өнімге жіберілетін шығыны төмендегі формуламен есептелінеді:

F= 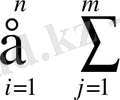a _ij b _ij x _ij (1. 21)

Сонымен бірге, әрбір кәсіпорынның жұмыс уақыты T-дан аспауға тиіс:

x _1j +x _2j + . . . +x _nj ≤T, j= 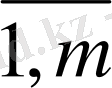(1. 22)

Шығарылатын өнім мөлшері тапсырмаға сәйкес болуы керек:

a _ij x ₁ +a _i2 x ₂ + . . . +a _im* х _m = N _i , i= 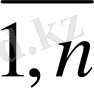(1. 23)

Бұған қосымша:

x _ij ≥0(i= 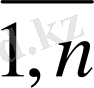j= 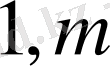) (1. 24)

Сонымен, тапсырманы кәсіпорындарға бөлу есебінің математикалық моделін былайша тұжырамдауға болады: Берілген (1, 21) максат функциясына минимум мән әперетін және (1, 22) - (1, 24) шарттарын қанағаттандыратын х _ij белгісіздердің мәндерін табукерек.

Тасымалдау есебі.

Күнделікті өмірде сызықтық бағдармалаудың жиі кездесетін есептерінің бірі тасымалдау есебі. Жаңа шаруашылық жағдайында, шығындарды қысқартуда тасымалдау есебінің шешімін табу өте маңызды.

Тасымалдау есебінің жалпы түрін қарастырайық.

Айталық, а _1, а _2, . . . , а _m m жабдықтаушыда әрқайсысында көлемі сәйкесінше а _1, а _2, . . . , а _m - ге тең біркелкі жүк мөлшері бар делік. Осы жүктерді b _1, b _2, . . . , b _n n тұтынушыға әрқайсысына сәйкесінше

в _1, в _2, . . . , в _n қажетті мөлшерінде тасымалдап жеткізу керек. Әрбір жабдықтаушыдан әрбір тұтынушыға жүктің жеке бір бөлігін тасымалдаудың шығыны белгілі делік және ол с _ij -ға тең болсын.

Барлық тұтынушылардың қажеттіліктерін толығымен қанағаттандыратын, барлық жабдықтаушылардағы жүк толығымен тасымалданатын және тасымалдау шығыны ең аз болатын тасымалдау жоспарын құру керек.

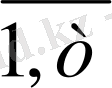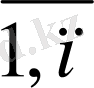Шешуі : есептің математикалық моделін құру үшін a _і жабдық таушыдан b _j тұтынушыға тасымалданатын жүк мөлшерін х _іj (і= ; j= ) деп белгілеп, есептің шартында берілген мәліметтерді жоспарлау кестесі деп аталатын мына төмендегі кестеге жазайық.

Жабдықтаушылар

Тұтынушылар

Жүк қ.

Жабдықтаушылар:

Тұтынушылар: b ₁

: b ₂

: . . .

Жүк қ.: b _n

Жабдықтаушылар: a ₁

Тұтынушылар: c ₁₁ x ₁₁

: c ₁₂ x ₁₂

: . . .

Жүк қ.: х _1n с _1n a ₁

Жабдықтаушылар: a ₂

Тұтынушылар: c ₂₁

: c ₂₂

: . . .

Жүк қ.: x _2n a ₂

Жабдықтаушылар: . . .

Тұтынушылар: . . .

: . . .

Жүк қ.: . . .

Жабдықтаушылар: a _m

Тұтынушылар: c _m1 x _{m 1}

: c _m2 x _m2

: . . .

Жүк қ.: c _mn a _m

Жабдықтаушылар: Тұтынушылардың қажеттілігі

Тұтынушылар: b ₁

: b ₂

: . . .

Жүк қ.: b _n

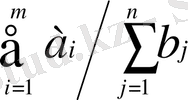
Есептің шартын жоспарлау кестесі арқылы жазу, оны шығару барысында өте ыңғайлы екенін ескерте кетейік және есепті түсіндірудің ең оңай жолы болып табылады.

Сонда і-жабдықтаушыдан j-тұтынушыға дейін тасымалданатын барлық жүк мөлшерінің шығынының бағасы ең аз болуы тиіс болғандықтан, тасымалдау есебінің мақсат функциясын мына түрде жазуға болады:

F=c ₁₁ x ₁₁ +c ₁₂ x ₁₂ + . . . +c _1n x _1n +c ₂₁ x ₂₁ +c ₂₂ x ₂₂ + . . . +c _2n x _2n + . . . +c _m1 x _m1

+c _m2 x _m2 + . . . +c _mn x _mn = 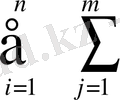c _ij* x _ij →min (1. 25)

Есептің шарты бойынша: а) барлық жабдықтаушылардағы жүк қоры толығымен тасымалдануы тиіс, яғни

x ₁₁ +x ₁₂ + . . . +x _1n =a ₁

x ₂₁ +x ₂₂ + . . . +x _2n =a ₂

- - - - - (1. 26)

x _m1 +x _m2 + . . . +x _mn =a _m

Және 2) барлық тұтынушылардың қажеттіліктері толығымен қанағаттандырылуы тиіс, яғни

x ₁₁ +x ₂₁ + . . . +x _m1 =b ₁

x ₁₂ +x ₂₂ + . . . +x _m2 =b ₂

- - - - - (1. 27)

x _1n +x _2n + . . . +x _mn =b _n

i-жабдықтаушыдан j-тұтынушыға тасымалданатын жүк мөлшері теріс емес санға тең болғандықтан, есептің математикалық моделіне оған енетін айнымалылардың теріс емесін шарты қосылады.

x _ij ≥0 (i= j= ) (1. 28)

Сонымен, тасымалдау есебінің (көлік есебінің) математикалық моделінің жалпы түрде жазылуын былайша беруге болады:

x _ij =b _j (j= )

x _ij ≥0(i= ; )

Теорема. Tасымалдау есебінің оптималь шешімі болуы үшін барлық жабдықтаушылардағы жүк қоры мөлшерінің барлық тұтынушылардың қажеттіліктерінің мөлшеріне тең болуы қажетті және жеткілікті, яғни

a _i = b _j (1. 29)

шартының орындалуы қажетті және жеткілікті.

(1. 29) шарты орындалатын тасымалдау есебін жабық моделді тасымалдау есебі жабық моделді тасымалдау есебі деп атайды. (1. 29) шарты орындалмайтын тасымалдау есебін ашық моделді тасымалдау есебі деп атайды. Ашық моделді тасымалдау есебін шешу үшін оны жабық моделді тасымалдау есебіне келтіреді. Егер a _i > b _j

болса, онда b _n+1 = a _i - b _j жалған тұтынушы қосылады, яғни

жоспарлау кестесіне бір бағана қосылады. Жүк бірлігін тасымалдаудың бағасы нөл деп алынады.

Егер а _i < b _j болса, онда а _m+1 = b _j - а _i жалған жабдықтаушы

қосылады яғни жоспарлау кестесіне бір қатар қосылады . Жүк бірлігін тасмалдау бағасы нөл деп алынады.

ІІ-тарау. Ауылшаруашылық есептерді жоспарлау модельдері.

2. 1. Математикалық модель түсінігі.

Математикалық модель ұғымы басқа ұғымдармен қатар, қатаң анықтамалар ғана емес, сонымен қатар математикалық модельдеуде орындалады. Ең болмағанда, бұл түсінік математиканың инженерлік тәжірибеде қолданылуымен тікелей байланысты, толық нақты мазмұнды көрсетеді. Мұндай ғылыми пәндер механика, физика және оның көптеген бөлімдерінде болатын ММ-дің реттелген жиыны. Қарастырылатын процестер мен болмыстардың қасиеттері бұл модельдеудің адекватты шағылысуының теориылық негіздемелерін шығарып салуды құрастырады. ММ-дің ғылыми пәндері арқылы математикамен өзара қатынасады. Бұл Карл Маркстың ескерту ойымен дәл келеді, өйткені кез-келген ғылым тек математикада қолданыс кезінде өзінің кемеліне жетеді.

Көптеген ғылыми - жаратылыстану бағыттарының даму этаптары табиғат заңдылықтарының танымы мен техникасының дамуында - ММ-дің зерттелетін процестері мен болмыстарында дәл және толықтай құрастырылған. Бірақ ғылымдар тарихы ММ-дің осы және басқа да дәлдік жағдайларын біліп қана қоймай, сонымен қатар ММ-дің божамдар ерекшелігі мен олардың нақты қорытындылары кері қайтару жағдайы болады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.