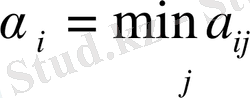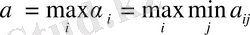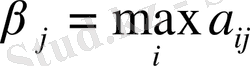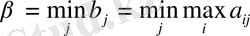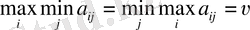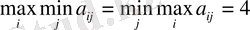Операциялық менеджмент үшін ойындар теориясының есептерін шешудің әдістемелік нұсқаулығы: геометриялық әдіс пен сызықтық программалау


МАЗМҰНЫ
КIРIСПЕ . . . . . . 3
Негізгі бөлім
1. Ойындар теориясы. . 4
2. Ойындарды жеңiлдету. Ойындар теориясының есептерiн шешудiң геомотриялық әдiсi . . . . . . 8
3. Ойындар теориясының есептерiн сызықтық программалау есептерiне ауыстыру . . . 16
Қорытынды . . . 19
Пайдаланылған әдебиеттер . . . 20
КIРIСПЕ
«Операциялық менеджмент» курсы экономикалық мамандықтардың студенттерi үшiн негiзгi пәндерiнiң бiрi болып табылады.
Қазiргi кезде жүйелердiң қызмет ету механизмдерiн сипаттайтын басқару принциптерiн және нақты әдiснаманы қолданусыз ұйымдастырылған жүйелердi зерттеу және басқару мүмкiн емес. Берiлген пробелдi басқару теориясының қазiргi бағыттарын қарастыру арқылы толтыруға болады. Жаңа теориялық бағыттардың жиыны ұйымдастырылған жүйелердiң басқару теориясын құрайды. Бұл қарама−қарсы емес мүдделi ойындар теориясы, шешiм қабылдау теориясы, белсендi жүйелер теориясы және ойындық модельдеу.
Әдiстемелiк нұсқаудың мақсаты - берiлген курсты зерттеу кезiнде студенттердiң өзiндiк жұмысын жеңiлдету. Әдiстемелiк нұсқауға ойындар теориясының есептерiн шешу материалдары кiредi, бұл есептердi шешудiң түрлi тәсiлдерi, ұйымдастырылған жүйелердiң басқару механизмдерi (тура және керi приоритеттер механизмдерi) келтiрiлген, “Ресурс” және “Жоспар” iскер ойындарынұйымдастыру және жүргiзу толық сипатталған. Сондай−ақ әдiстемелiк нұсқауда өзiндiк жұмыс үшiн есептер берiлген.
Негізгі бөлім.
І тарау. ОЙЫНДАР ТЕОРИЯСЫНЫҢ НЕГIЗДЕРI
Ойындар теориясы - қақтығыс немесе белгiсiздiк жағдайында оптималды шешiм қабылдаудың математикалық модельдер теориясы. Бұл жерде қақтығыс антогонистiк ретiнде қарастырылуы мiндеттiемемс; қақтығыс ретiнде кез-келген қайшылықты алуға болады.
Мысалы, олигополиялық нарықтағыбiр компанияның шығарылған өнiмiнiң көлемi немесе баға қалыптастыру бойынша шешiмi бұл нарықтағы басқа қатысушылардың табысының көлемiне әсер етедi. Осыған сәйкес пайданы максималдау үшiн менеджер өз шешiмдерiнiң бәсекелестерiнiң қызметiне және олардың әсерiне мән беру керек.
Ойындар теориясы - шешiмдердiң ең ауқымды спектрiн талдау үшiн қолданылатын негзгi құрал. Ойындар теориясының мазмұны, бiрiншiден, ойыншылардың ойындарда оптималды iс-әрекеттерiнiң принциптерiн орнатудан тұрады. Екiншiден, бұл принциптердi қолдану нәтижесiнде пайда болатын жағдайлар кездесетiнiн дәлелдеу, үшiншiден, iс-жүзiнде табу әдiстерi құрастырудан тұрады.
Ойындар теориясында ойындардың түрлерiнiң тұрақталынған классификациясы жоқ. Бiрақ белгiлi критерийлер бойынша кейбiр түрлерiн бөлiп көрсетуге болады.
Ойыншылар саны . Егер ойында екi қатысушы болса, онда ойынды n ойыншысы бар ойынға жатқызады. Екi қатысушысы бар ойындар өте қызық болып келедi. Олар математикалық жағынан терең ойластырылған және практикалық қосымшаларда үлкен библиографияға ие.
Ойынның стратегияларының саны. Бұл критерий бойынша ойындар ақырғы және ақырсыз болып бөлiнедi. Ақырғы ойында ойыншылардың әрқайсысының мүмкiн стратегияларының саны ақырғы болып келедi. Егер ойншылардың бiреуiнiң болсын стратегиясы ақырсыз болса, онда ойын ақырсыз.
Қатысушылардың өзарақатынастары . Ойынның берiлген критерийiне сәйкес ойындар кооперативтiк, коалициялық және коализациялық емес болып бөлiнедi. Егер ойыншылардың келiсiмге келуге, коалиция құруға құқығы жоқ болса, мұндай ойын коалициялық емес; ал егер ойыншылар келiсi алса, коалиция құра алса, онда коалициялық болып табылады. Кооперативтiк ойын - коалициялар алдын ала анықталған ойындар.
Ұтыстардың характерлерi . Бұл критерий нольдiк және нолдiк емес сомалы ойындарды классификациялауға мүмкiндiк бередi. Нольдiк сомасы бар ойын “барлық ойыншылардың ұтыстарының сомасы әр ойында нольге тең” деген шартты қанағаттандырады. Нольдiк сомасы барекi ойыншының ойынын антогонистiк ойындар класына жатады. Бұл жағдайда бiр ойыншының ұтысы екiшiсiнiң ұтылысына тең. Нольдiк сомасы бар ойындардың мысалына көптеген экономикалық ойындар жатады. Оларда барлық ойыншылардың жалпы капиталы ойыншылар арасында қайта бөлiнедi, бiрақ өзгермейдi. Нольдiк емес сомасы бар ойындарға да экономикалық ойындардың көбiн жатқызуға болады. Қатысу құқығы үшiн ақы төлейтiн ойын нольдiк емес сомасы бар ойын деп аталады.
Ұтыстардың функкциялардың түрлерi . Бұл критерий бойынша ойындар матрицалық, биматрицалық, үздiксiз, дөңес, сепарабельдi және т. б. болып бөлiнедi. олардың кейбiреуiн түсiндiрiп өтейiк.
Матрицалық ойын - нольдiк сомалы екi ойыншысы бар ақырғы ойын. Жалпы жағдайда оның төлемдiк матрицасы төртбұрышты болып келедi.
1- кесте
Матрицаның жолының номерi бiрiншi ойыншының қабылдаған стратегиясының номерiне сәйкес келедi. Баған номерi екiншi ойыншының стратегиясына сәйкес келедi. Бiрiншi ойыншының ұтысы матрицаның элементi болып табылады. Екiншi ойыншының ұтысы бiрiншi ойыншының ұтылысына тең. Олар сызықтық программалау тәсiлдерiмен шешiле алады. Биматрицалық ойын - нольдiк емес сомалы екi ойыншысы бар ақырғы ойын. әрқайсысының ұтысы қатары бiрiншi ойыншының стратегиясына, бағаны екiншi ойыншының стратегиясына сәйкес келетiн матрицамен берiледi. Бiрақ бiрiншi матрицаныңэлементi бiрiншi ойыншының ұтысын, ал екiншi матрицаның элементi екiшi ойыншының үтысын көрсетедi. Биматрицалық ойындар үшiн де ойыншылардың оптималды iс әрекетiнiң теориясы құрастырылған.
Егер стратегиясына байланысты әрбiр ойыншының ұтыстарының функциясы үздiксiз болса, онда ойын үздiксiз , егер ұтыстар функциясы дөңес болса, онда ойын дөңес болып табылады.
Егер ұтыстар функциясы бiр аргументтiң функциялардың сомасына бөлiне алса, онда ойын сепарабельдi болып табылады.
Жүрiстер саны. Ойынның бұл критерийiне сәйкес ойындарды бiр қадамдық және көп қадамдық деп ажыратады. Бiр қадамдық ойындар әрбiр ойыншының бiр қадамынан кейiн аяқталады. Осылайша, матрицалық ойында ойыншылардың әрқайсысының бiр қадамынан кейiн ұтыстардың бөлiнiсi жүредi. Көп қадамдық ойындар позициялық стохастикалық, дифференциалды бола алады.
Қатысушылардың ақпараттандырылуы. Берiлген критерий бойынша толық және толық емес ақпараты бар ойындарды ажыратады . Егер әрбiр ойыншы ойынның әрбiр қадамында басқа ойыншылардың алдыңғы қадамдарда қолданған стратегияларын бiлсе, бұл ойын толық ақпараты бар ойын ретiнде анықталады. Егер әрбiр ойыншы ойынның әрбiр қадамында басқа ойыншылардың алдыңғы қадамдарда қолданған стратегияларының бәрiн бiлмесе, бұл ойын толық емес ақпараты бар ойын ретiнде анықталады. Кейiнiрек бiз толық ақпараты бар ойынның шешiмi болатынын дәлелдеймiз. Таза стратегиялар кезiнде ертоқым нүктесi оның шешiмi болады
Ақпараттың толықсыздығының деңгейi . Бұл критерий бойынша ойындар статистикалық және стратегиялық болып бөлiнедi. Табиғаты бар ойындарды статистикалық ойындарға жатқызады. Статистикалық ойындарда табиғат күйiнiң ықтималдығының таралымы бағаланатын немесе есептелiнетiн статистикалық тәжiрибе негiзiнде ақпарат алу мүмкiндiгi бар. Ойыншылар мен коалициялардың оптималды iс әрекеттеттерiнiң принциптерiнiң көбiсi оптималды iс әрекет нәтижесiнде пайда болған жағдайдан ауытқу тұрақтылық принципiнiң сипатына ие, немесе өздiгiнен тиiмсiз болу керек, немесе мұндай ауытқудан кейiн оптималды iс әрекет көмегiмен жетуге болатын жаңа жағдайға пайдамен жету мүмкiндiгi пайда болу керек.
Ойын классификациясына қолданылатын тәсiлдер туралы мәлiмет алғаннан кейiн ойын бағалары туралы айтуға болады.
m x n ұтыстардың матрицасымен берiлген матрицалық ойынды қарастырайық, мұндағы
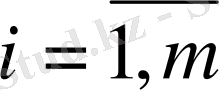 қатарлар саны, ал
қатарлар саны, ал
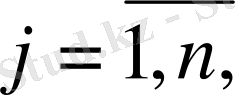 бағандар саны (1−кестенi қара) . Ең тиiмсiз жағдайдағы максималды кепiлдi нәтиже алу принципiн қолданайық. Бiрiншi ойыншы екiншi ойыншының максималды ұтысын қамтамасыз ететiн стратегияны ұстануға тырысады. Осыған сәйкес екiншi ойыншы бiрiншi ойыншының минималды ұтысын қамтамасыз ететiн стратегияны ұстануға тырысады. Осы екi тәсiлдеменi қарастырайық.
бағандар саны (1−кестенi қара) . Ең тиiмсiз жағдайдағы максималды кепiлдi нәтиже алу принципiн қолданайық. Бiрiншi ойыншы екiншi ойыншының максималды ұтысын қамтамасыз ететiн стратегияны ұстануға тырысады. Осыған сәйкес екiншi ойыншы бiрiншi ойыншының минималды ұтысын қамтамасыз ететiн стратегияны ұстануға тырысады. Осы екi тәсiлдеменi қарастырайық.
Бiрiншi ойыншының iс−қимылы.
Ол ең тиiмсiз жағдайдағы максималды кепiлдi нәтиже алу керек. Яғни осы шартқа жауап беретiн таза стратегияны таңдау кезiнде ол тиiмсiз шарттардағы кепiлдi нәтиже таңдау керек, яғни
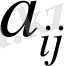 өз ұтысының ең кiшiсiн, оны
өз ұтысының ең кiшiсiн, оны
деп белгiлеймiз, ең тиiмсiз шарттар кезiнде бұл кепiлдi нәтиже максималды болу үшiн барлық
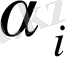 iшiнен ең үлкн мәнiн таңдау керек. Оны
iшiнен ең үлкн мәнiн таңдау керек. Оны
 деп белгiлеп, ойынның таза төменгi бағасы деп атаймыз («максимин») :
деп белгiлеп, ойынның таза төменгi бағасы деп атаймыз («максимин») :
осылайша, α. Элементiне сйкес келетiн матрицаның қатары макимин стратегиясына сәйкес келедi. Екiншi ойыншы қандай стратегия қолданбаса да бiрiншi ойыншы өзiне α кем емес ұтыс жасап алды. Бiрiншi ойыншының оптималды iс−әрекетi осындай.
Екiшi ойыншының iс−әрекетi.
Өзiнiң оптималды стратегияларымен ол бiрiншi ойыншының үтысын азайтқысы келедi, сондықтан әрбiр j - iншi таза стратегия кезiнде ол әрбiр j - iншi бағанда
егер екiншi ойыншы j - iншi стратегияны қабылдаса максиминдi ұтылысының көрсеткiшiн iздейдi, яғни бiрiншi ойыншының максималды ұтысын анықтайды. өзiнiң барлық n j-iншi таза стратегиялар iшiнен бiрiншi ойыншы минималды ұтыс алатындай стратегияны таңдайды, яғни ойынның жоғарғы бағасын анықтайды («минимакс») :
екiншi ойыншы жоғарыда көрсетiлген өзiнiң таза стратегияларды таңдау нәтижесiнде бiрiншi ойыншының β−дан артық ұтуына жол бермейдi. Осылайша, минимаксты β элементi орналасқан төлем матрицасының бағанымен берiледi. (1−кестенi қара) .
Ол екiншi ойыншының оптималды таза кепiлдi стратегиясы болып табылады, егер ол бiрiншi ойыншының iс−қимылы туралы мәлiмет бiлмесе.
Ойынның
 таза бағасы - берiлген ойынның бағасы, егер ойынның жоғарғы және төменгi бағасы сәйкес келсе
таза бағасы - берiлген ойынның бағасы, егер ойынның жоғарғы және төменгi бағасы сәйкес келсе
бұл жағдайда ойын ертоқым нүктесi бар ойын деп аталады
Мысал 1. Ойынның берiлген матрицасында ойынның төменгi және жоғарғы бағаларын анықтау және максиминдi және минимаксты стратегияларын көрсету. Стратегиялардың
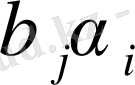 белгiлеулерi бар ойын матрицасы берiлген (2-кесте) .
белгiлеулерi бар ойын матрицасы берiлген (2-кесте) .
2-кесте
Шешiмi. Ойынның төменгi бағасын анықтайық:
(
бағанын қара)
Ойынның жоғарғы бағасын анықтайық:
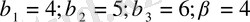 (
(
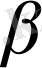 қатарын қара) .
қатарын қара) .
Осылайша,
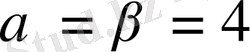 , яғни
, яғни
яғни,
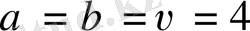 -
А
2
және В
1
стратегиялар кезiнде ойынның таза бағасы, бұдан шығатыны бұл ойынның ертоқым нүктесi бар.
-
А
2
және В
1
стратегиялар кезiнде ойынның таза бағасы, бұдан шығатыны бұл ойынның ертоқым нүктесi бар.
Мысал 2. 2 берiлген тиiмдiлiктегi минимаксты және максиминдi стратегияларды анықтаймыз.
Ш е ш iм i. максиминдi стратегиюны анықтайық:
α 1 =2, α 2 =2, α=4.
Максиминдi стратегия -А 2 қатары
3−кесте
Минимаксты стратегиюны анықтайық:
β 1 = 8; β 2 = 7; β 3 = 9; β 3 = 10; β = 7;
Минимаксты стратегия - В 2 . бағаны, мұндағы α < β, бұдан шығатыны, бұл жерде ертоқым нүктесi жоқ.
Егер ойын матрицасында өз қатарында минималды және өз бағанында максималды болып табылатын элемент болса, онда ол ертоқым нүктесi болып табылады. Айталық, ертоқым нүктесi бар ойында бiр ойыншы ертоқым нүктесiн ұстанады делiк, егер екiншi ойыншы ертоқым нүктесiн ұстанса, ол да жақсы нәтижеге жетедi. Ойыншының ең жақсы әрекетi оның ұтысын азайтпауға тиiс. Берiлген жағдайда ойын шешiмi:
- 1 ойыншының таза стратегиясы;
- 2 ойыншының таза стратегиясы;
- ертоқым нүктесi.
Оптималды таза стратегиялар - бұл ертоқым нүктесiн құрайтын таза стратегиялар.
Ертоқым нүктесi жоқ ойында, егер бiрiншi ойыншы екiншi ойыншының қабылдаған стратегиясы туралы мәлiметi болса, онда ол максиминдi стратегияға сәйкес келмейтiноптималды стратегия қабылдай алады.
Мысал 3. Ойын матрицасы берiлген
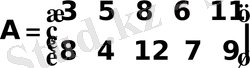 .
.
Айталық, бiрiншi ойыншыға екiншi ойыншының минимаксты стратегия қабылдағаны белгiлi болсын. Бiрiншi ойыншы В 2 - 2 ойыншының стратегиясы (β=5) шартында оптималды стратегияны таңдау керек.
Ш е ш i м i: 1 ойыншының максиминдi стратегиясын анықтайық: α 1 =3, α 2 =4, α=4.
1 ойыншының стратегиясы - А 2 - максиминдi.
Бiрiншi ойыншы үшiн оптималды стратегия таңдайық. Бiрiншi ойыншыға α=4 ұтысын беретiн
А
2
максиминдi стратегиясы емес
 сәйкес келетiн стратегияны таңдаймыз. бұл жағдайда оның кепiлдi максималды ұтысы β=5, ойынның жоғарғы бағасына тең, сондықтан ол екiншi ойыншы
В
2
стратегиясын таңдағанын бiле отырып,
А
1
өзiнiң оптималды стратегиясын таңдайды. .
сәйкес келетiн стратегияны таңдаймыз. бұл жағдайда оның кепiлдi максималды ұтысы β=5, ойынның жоғарғы бағасына тең, сондықтан ол екiншi ойыншы
В
2
стратегиясын таңдағанын бiле отырып,
А
1
өзiнiң оптималды стратегиясын таңдайды. .
Стратегия оптималды болады, егер оның қолданысы ойыншыны басқа ойыншының кез келген мүмкiн стратегиялары кезiнде ең үлкен кепiлдi ұтыспен қамтамасыз етсе.
3−мысалда егер ойыншыға екiншi ойыншынының iс−қимылдары белгiлi болса, максиминннен асатын ұтыс ала алмайтын жағдайлар көрсетiлген.
Ұқсас жағдайларда ойынды көп рет қайталаған жағдайда бiрiншi ойыншы үшiн максиминнен асатын кепiлдi орташа ұтысқа жетуге болады.
ІІ тарау. ОЙЫНДАРДЫ ЖЕҢIЛДЕТУ
ОЙЫНДАР ТЕОРИЯСЫНЫҢ ЕСЕПТЕРIН ШЕШУДIҢ ГЕОМЕТРИЯЛЫҚ ӘДIСI
Егер m х n ойынынын ертоқым нүктесi болмаса, онда оны iздеу, әсiресе, m и n үлкен мәндерiнде қиынға түседi. Бұл есептi жеңiлдетуге болады, егер ойынды алдын ала стратегиялардың артығын сызып тастау арқылы олардың санын қысқартсақ
Артық стратегиялардың екi түрi болады: қайталайтын және тiптен тиiмсiз.
Мысалы,
4−кесте
матрицалы И ойынын қарастырайық. А 3 стратегиясы А 1 стратегиясын дәл қайталайтынын матрицадан көрiнiп тұр, сондықтан бұл екеуiнiң бiреуiн сызып тастауға болады. Ары қарай А 1 және А 2 қатарларын мүшелеп салыстырсақ, А 2 қатарының барлық элементтерi А 1 қатарының элементтерiнен кiшi екенi көрiнiп тұр. Сондықтан А 2 статегиясы ұтқымыз келетiн бiз үшiн тiптен тиiмсiз. А 3 және А 2 сызып тастап, матрицаны жеңiлiрек түрге келтiремiз:
5−кесте
Ары қарай қарсыласымыз үшiн В 3 стратегиясы тiптен тиiмсiз екенiн байқаймыз . оны да сызып тастаймыз, матрица келесi түрге келдi:
6−кесте
Осылайша, 4 х 4 ойыны 2 х 3 ойынына келтiрiлдi.
Кейде таза стратегиялар орнына аралас стратегиялар енгiзу арқылы жасанды жолмен жеңiлдетуге болады. Айталық, мысалы,
7−кесте
Матрицалы 3 х 4 ойны бар. Матрицаны қарастыра отырып, B 1 және B 2 ; B 3 және B 4 бағандарының, А 1 және А 2 қатарларының элементтерiнiң симметриясына байланысты бұл стратегиялар шешiмге кiрсе де, р 1 = р 2 , q 1 = q 2 , q 3 = q 4 тең ықтималдықтарымен ғана. Осы жерде бiр ой туады: алдын ала B 1 және B 2 стратегияларын жартылай B 1 −ден, жартылай B 2 −ден тұратын В 12 аралас стратегиясына бiрiктiру, дәл осылайша B 3 және B 4 стратегияларымен жасаймыз, яғни тең ½ ықтималдықтары бар B 3 және B 4 стратегияларын В 34 бiр аралас стратегиясына бiрiктiремiз.
Матрица келесi түрге келедi.
8−кесте
Ендi, егер қарсыласымыз B 12 , B 34 стратегияларын қолданса, А 1 және А 2 стратегиялары бiр бiрiн қайталайтынын көремiз. Олардың бiрiн сызып тастап, келесi 2 х 2 матрицаны аламыз.
9−кесте
Осылайша, 3 х 4 ойыны 2 х 2 ойынына келтiрiледi.
2 х 2 ойыны ақырғы ойынның ең қарапайым мысалы болып табылады, мүнда әр ойыншының екi стратегиясы бар. 2 х 2 матрицасы бар ойынды қарастыорайық:
11−кесте
Мүнда екi жағдай кездеседi:
- Ойынның ертоқым нұктесi бар;
- Ойынның ертоқым нұктесi жоқ.
Бiрiншi жағдайда: ойынның шешiмi - ертоқым нұктесiнде қиылысатын стратегиялар жұбы. Егер 2 х 2 мұндай ойынның ертоқым нүктесi болса, онда бұл ойында стратегиялардың әйтеуiр бiреуi қайтайлайтын немесе тiптен тиiмсiз ретiнде алынып тасталатынын дәлелдеу қиынға түспейдi. Бұны дәлелдемей−ақ қойайық
Екiншi жағдайды қарастырайық: айталық 2 х 2 екiншi матрицасында ертоқым нүктесi жоқ. Мұнда ойынның жоғарғы бағасы төменгi бағасына тең емес: α ≠ β. Ойынның шешiмi аралас стратегиялармен берiлуге тиiс. Бұл шешiмдi табайық, яғни
Sa* = (p 1 , p 2 ) ; Sb* = (q 1 ; q 2 ) .
Оптималды аралас стратегиялар жұбын анықтаймыз.
Алдымен Sa* оптималды аралас стратегияны анықтаймыз. Активтi стратегиялар теоремасына сәйкес, егер бiз осы стратегияны ұстансақ, онда қарсыласымыздың қимылына тәуелсiз, ұтысымыз v ойын бағасына тең болып қала бередi. 2 х 2 ойынында қарсыласымыздың екi стратегиясы да активтi болып табылады. Яғни, егер бiз өзiмiздiң Sa* = (p 1 , p 2 ) оптималды стратегиясын ұстансақ, қарсыласымыз ұтысты өзгертпей өзiнiң таза стратегияларының кез−келгенiн қолдана алады. Бұдан екi теңдеу аламыз:
a
11
р
1
+ а
21
р
2
=
 (1)
(1)
a
12
p
1
+ a
22
p
2
=
 ,
,
р 1 + р 2 = 1 шартын ескере отырып, алатынымыз:
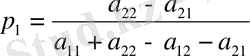 ,
,
(2)
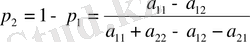
Ойынның v бағасын р 1 , р 2 мәндерiн (1) теңдеудiң кез−келгенiне қойып табамыз:
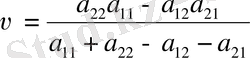 . (3)
. (3)
Осылайша
a 11 q 1 + a 12 q 2 = v (4)
a 21 q 2 + a 22 q 2 = v
теңдеулерiнен қарсыласымыздың оптималды стратегиясы табылады:
Sb* = (q 1 ; q 2 ) .
Бұдан шығатыны
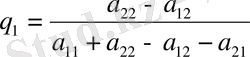
q 2 = 1 - q 1 (5)
2 х 2 ойынының шешiмiне ыңғайлы геометриялық интерпретация беруге болады. Айталық,
12−кесте
матрицасы бар 2 х 2 ойыны берiлсiн .
Ұзындығы бiрге тең абцисса осiнiң учаскесiн алайық (1−сурет) . Учаскенiң сол шетi ( х = 0 абсциссасы бар нүкте) А 1 стратегиясын, учаскенiң оң шетi (х = 1) -А 2 стратегиясын көрсетедi; учаскенiң барлық аралық нүктелерi А ойыншының аралас стратегияларын көрсетедi, мұнда А 1 стратегияның р 1 ықтималдығы S A нүктесiнен учаскенiң оң шетiне дейiнгi арақашықтыққа тең болады, ал А 2 стратегиясының р 2 ықтималдығы - сол шетiне дейiнгi қашықтыққа тең болады. А 1 және А 2 нүктелерi арқылы абциссалар осiне екi перпендикуляр жүргiземiз: I - I осi және II - II осi. I - I осiнде -А 1 стратегиясы кезiндегi, II - II осiнде-А 2 стратегиясы кезiндегi ұтыстарды белгiлеймiз.
I II
I II
B 2 B 1
B 1 N
a 11 a 12 B 1 ν a 12
a 11 B 2
A 1 A 2 a 22
0 1 0
p 2 S A p 1 p 2 S * A p 1 1 x
1−сурет 2−сурет
айталық, қарсыласымыз В 1 стратегиясын қолданады, ол сәйкесiнше I - I және II - II осьтерiнде а 11 және а 21 ординаталары бар нүктелерiн бередi. Осы нүктелер арқылы В 1 В 1 түзуiн жүргiзейiк. Кез−келген S A = (р 1 ; р 2 ) аралас стратегиясы кезiнде бiздiң В 1 В 1 түзуiнде ұтысымыз абциссалар осiнде S A нүктесiне сәйкес келетiн, кесiндiнi р 2 : р 1 қатынасына бөлетiн N нүктесiмен көрсетiледi. В 1 В 1 түзуiн шартты түрде «В 1 стратегиясы» деп атаймыз.
I II
B 2 a 21
ν = a 22
a 12 B 1
a 11
0 1 x
p 2 S * A =A 2
3−сурет
Дәл осы әдiспен В 2 стратегиясы тұрғызылары анық. (2−сурет) .
Бiзге минималды ұтысымыз максималды ға айналатын S A * оптималды стратегиясын табу керек. Ол үшiн В 1, В 2 стратегиялары кезiнде ұтыстың төменгi шегiн тұрғызамыз, яғни 2−суретте қалың сызықпен крсетiлген В 1 NВ 2 . Осы шекарада А ойыншының оның кез келген стратегиясы кезiнде минималды ұтысын қоямыз. Ұтыс максимумға жететiн N нүктесi ойынның бағасын және шешiмiн анықтайды. N нүктесiнiң ординатасы v ойынның бағасы екенiн байқауға болады, оның абциссасы р 2 тең, ал кесiндiнiң сол жағына дейiгi қашықтығы р 1 тең, яғни S A * нүктесiнен кесiндiнiң аяғына дейiнгi қашықтығы А ойыншының оптималды аралас стратегиясында А 2 және А 1 стратегияларының р 2 және р 1 ықтималдықтарына тең.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz