Үшбұрышты шекті элементтердің негізгі математикалық өрнектері мен қатаңдық матрицаларын құру алгоритмдері және USBURS программасымен нақты есептерді шешу


МАЗМҰНЫ
беті
Кіріспе . . . 4
I - Бөлім ҮШБҰРЫШТЫ ШЕКТІ ЭЛЕМЕНТТЕРДІҢ НЕГІЗГІ
МАТЕМАТИКАЛЫҚ ӨРНЕКТЕРІ МЕН АЛГОРИТМДЕРІ . . . 5
1. 1 Шекті элементтер әдісінің негізгі түсініктері . . . 5
1. 2 Үшбұрышты элементтің ығысу функциялары . . . 6
1. 3 Деформация мен кернеудің шекті элементтік өрнектері . . . ……. . 8
1. 4 Элементтің және жүйенің қатаңдық матрицаларын құру алгоритмдері . . . 11
II - Бөлім ЭЛЕМЕНТ ПЕН ЖҮЙЕНІҢ ҚАТАҢДЫҚ МАТРИЦАЛАРЫН
ІС ЖҮЗІНДЕ ҚҰРУ . . . 13
2. 1 Жүйенің қатаңдық матрицасын құрудың негізгі әдісі . . . 13
2. 2 Жүйенің қатаңдық матрицасын құрудың басты ережесі . . . 17
2. 3 Екі элементтен тұратын жүйенің қатаңдық матрицасын құру . . . 20
2. 4 Үш элементтен тұратын жүйенің қатаңдық матрицасын құру . . . 22
2. 5 Көп элементке бөлген жүйенің қатаңдық матрицасын құру . . . 26
III - Бөлім ШЕКТІ ЭЛЕМЕНТТЕР ӘДІСІМЕН НАҚТЫ ЕСЕП ШЕШУ . . . 30
3. 1 Зенкевичтің тесттік есебі туралы . . . 30
3. 2 Шекті элементтер әдісінің қысқаша «USBURS» программасын құру . . . 32
3. 3 Зенкевичтің есебін «USBURS» программасымен шешу нәтижелері . . . 36
Қортынды . . . 38
Әдебиеттер . . . 38
КІРІСПЕ
Ғылым мен техникада, құрылыс, жол қатынастары, ғарышқа ұшу аппараттары, Күн жүйесі планеталарының орнықтылығы, атом реакторларының беріктігі, газ, мұнай, кен өндірісі, гидротехника, жер қыртысының орнықтылығы, жерсілкінісінің аймақтары, жер асты, жер бетінің сейсмоберік құрылыстары, оқу процесі, өмірдің тағы басқа көптеген салаларында кең қолданылып, әрі уақыт өткен сайын қатты қарқынмен дамып келе жатқан қазіргі заманғы математикалық аса қуатты сандық әдістердің бірі шекті элементтер әдісі (ШЭӘ) . Бұл әдіс бүгіндері университеттердің оқу жоспарларына негізгі пәндердің бірі ретінде толық енді. Дж. Норри мен Ж. де Фриздің 1976 жылға дейінгі мәліметтері бойынша шекті элементтер әдісіне арналып 17752 жұмыс жарияланған болса, бүгіндері оны санау мүмкін де емес әрі мағынасы да жоқ. Бұл әдіс математикада қашан, қалай пайда болды деген тарихына қысқаша тоқалайық. Оның алғашқы белгілері Рицтің (1909), Галеркиннің (1915), Куранттың(1943), Прагер мен Сингтің (1947), Аргиристің (1954 - 1955), Тернердің (1956) жұмыстарынан басталады. Шекті элементтер туралы ең алғашқы ұғым мен түсінікті 1956 - Тернер енгізді. Ал «шекті элементтер» терминін (1960) Клафф енгізді.
1960 - жылдардан соң ШЭӘ - нің дамуына Зенкевич, Аргирис, Айронс, Андерсон, Оден, Галлагер тағы басқа американдық мамандардың үлесі көп. Бұл әдістің даму барысын бір ізге, жүйеге түсіріп, іс жүзінде қолдануға лайықтап оқулықтар мен монографиялар жазған Зенкевич, Батье, Вильсон, Оден, Стренг, Фикс, Норри; Фриз, Галлагер, Сегерлиндтердің сіңірген еңбектері айрықша. ШЭӘ - нің негізін баяндаудағы біздің басты мақсатымыз - оны түсініп, игерудің, қарапайым есептерді шешуге, дипломдық және күндізгі және сыртқы бөлім студенттерінің, ғылыми жұмыстарына ғана емес сонымен қатар мектеп оқушыларының олимпиадаларға қатынасуларына дайындалуда да төте жолдармен қолданып игерулеріне мүмкіндік жасау. Сондықтан негізгі теңдеулер мен формулаларды, өрнектерді матрицалық түрде жазумен қатар оларды толық ашып, тікелей программалауға қолайлы болуы үшін алгоритм түрінде баяндалды.
Айта кететін мәселе - шекті элементтердің қолданылу түрі сан алуан болғанымен оны тез түсініп, игеруге көп септігін тигізетін серпімділік есептері. Оның ішінде физиканың механика бөліміндегі мектеп курсынан белгілі Гук заңының есептері. ШЭӘ өзінің дамуын о бастан осы серпімділік есептерін шешуге қолданылудан бастау алған болатын. Табиғатта серпімділік қасиеті жоқ дене болмайды. Абсолютті қатты дене ұғымының өзі шартты түсінік. Тау - кен тасы, темір, көмір, шойын, болат, гранит, алмаз тағы басқа кез - келген қатты деген заттардың барлығының да түрліше серпімділік шектері бар. Кез - келген зат серпімділік қасиеттері бойынша изотропты немесе анизотропты болып келеді. Изотропты дегеніміз серпімділік қасиеті кеңістік бойынша барлық бағытта бірдей болып келетін денелер. Ал серпімділігі әр бағытта әртүрлі болып келетін денелерді анизотропты дейді. Басқаша айтқанда изотропты дегеніміз түзілімдік құрылысы біртекті де анизотропты - әртекті.
Дипломдық жұмыста үшбұрышты элементтердің негізгі математикалық өрнектері мен алгоритмдері теориялық және практикалық тұрғыдан толық келтіріліп, Фортран тілінде құрылған программа тексті, оның көмегімен шешілген тесттік есеп нәтижелері келтірілді. Жүйенің қатаңдық матрицасын симметриялық және ленталық етіп құрды іс жүзінде қалай құрылатындығы көрсетілді. Әдістемелік тұрғыдан алдымен бір элементтен, сонан соң екі, үш бес, жеті элементтерден тұратын зерттеу облысының қатаңдық матрицаларын түрліше құру жолдары егжей - тегжейлі қарастырылып, О. Зенкевичтің тесттік есебін келтіріліп, оны жаңа әдіспен тиімді етіп шешуге болатындығы көрсетілді Фортран тілінде құрылған « USBURS » атты программа тексті толық келтіріліп, оның итерация әдісіне арнап құрылған нұсқасы мен алынған нәтижелер толығымен талқыланып келтіріледі.
I - Бөлім ҮШБҰРЫШТЫ ШЕКТІ ЭЛЕМЕНТТЕРДІҢ НЕГІЗГІ
МАТЕМАТИКАЛЫҚ ӨРНЕКТЕРІ МЕН АЛГОРИТМДЕРІ
1. 1 Шекті элементтер әдісінің негізгі түсініктері
Шекті элементтер әдісінің (ШЭӘ) - нің негізгі түсінігі О. Зенкевич бойынша төмендегідей /1/, /2/.
а) Тұтас орта ойша сызықтармен немесе ауданшалармен шартты түрде бірнеше шекті элементтерге бөлінеді. Тек ойша ғана болғандықтан қарастырып отырған ортаның тұтастығы алғашқы күйіндей бұлжытпай сақталады.
б) Элементтер бірімен бірі өзара түйісу нүктелері арқылы ғана байланысады. Бұл жердегі іздейтін негізгі белгісізіміз осы нүктелердің ығысулары.
в) Әрбір шекті элементтің ішіндегі ығысуды бірден бір жолмен сипаттайтын функциялар жүйесі таңдалады.
г) Ығысу функциясы элементтің ішкі деформациясын төбелеріндегі нүктелердің ығысулары бойынша анықтайды. Бұл деформациялар элементтің бастапқы белгілі деформациясы мен серпімділік қасиеттері бойынша оның ішіндегі және шекараларындағы кернеулерді табуға мүмкіндік береді.
д) Шекарадағы кернеуді және таралған күштерді теңестіретін күштер жүйесі анықталады.
Нақты есепті шешу үшін элементтің және ығысу функцияның тиімді түрін қолдана білу аса жауапты мәселе. Ол зерттеушінің шеберлігі мен тапқырлығына байланысты. Есептің жуықтап дұрыс шешілуінің өзі осы мәселеге тікелей тәуелді.
Жазықтық жағдайындағы есептерді шешу зерттелетін облыстың геометриялық пішініне қарай үшбұрышты немесе төртбұрышты олардың өзі бірінші ретті немесе екінші ретті түрде таңдалынады.
Зенкевич, Вебеке, Айронс, Аргиристердің арнайы зерттеп көрсетулеріне қарағанда үшінші, төртінші ретті элементтерді пайдалану тиімсіз. Біріншіден ақталмайтын күрделі әрі тым ұзақ математикалық өрнектерді жазуға тура келеді. Екіншіден есептің шешілу дәлдігі артпайды. Тағы бір келеңсіздігі есептеуге көп уақыт кетеді. Біздің арнайы зерттеулеріміз де бұл тұжырымның рас екендігін көрсетті. Оған алдағы үшінші бөлімде нақты тесттік есепті шешу арқылы көз жеткізіледі.
Жалпы шекті элементтер әдісінің минимизациялау процесімен сәйкес екендігін алғаш рет Клоуг, Змелтерлер байқаған. Бірақ жоғарыда айтқандай Курант, Прагер, Сингтер кезінде осыған ұқсас ұсыныстар жасаған болатын. Біз бұл жерде функцияны минимизациялауға тоқталмаймыз. Ескертеріміз вариациялық қойылым мүмкін болатын есептердің кез - келгеніне шекті элементтер әдісін қолдануға болатындығы.
Жоғарыда айтылған бес қадам орындалғаннан кейін Гук заңына негізделіп жүйенің қатаңдық матрицасы құрылады. Шекті элементтер әдісінің мәнісі де, тоқ етер түйінді жері де, бар құпиясы мен қиындығы да осында. Қатаңдық матрицасын құра білсек сыртқы күш векторы арқылы тепе - теңдікті сипаттайтын алгебралық сызықты теңдеулер жүйесі құрылды деген сөз. Әрі қарай ол жүйені жоғары математиканың кез - келген әдісін қолданып шығара отырып белгісіз болып отырған ығысу векторларын тағы басқа шамаларды сатылай отырып таба аламыз.
1. 2 Үшбұрышты элементтің ығысу функциялары
Серпімділік теориясының жазық есептерінде есептік облыстың көлденең қимасы не жазық деформация немесе жазық кернелген күйге келетіндігі белгілі /1/, /2/, /3/, /4/, /5/.
Шекті элементтер әдісінде бұл екі жағдайда да ығысу өрістері
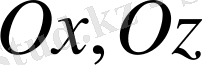 немесе
немесе
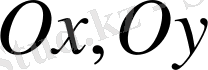 декарттық координаталарының бағыттарындағы
декарттық координаталарының бағыттарындағы
 ,
,
 , құраушылары арқылы анықталады. Ал деформация мен кернеулердің жазық есептерде үш - үштен құраушылары болады.
, құраушылары арқылы анықталады. Ал деформация мен кернеулердің жазық есептерде үш - үштен құраушылары болады.
Төбелері
 ,
,
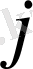 ,
,
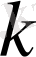 деп белгіленген типтік кәдімгі үшбұрыш 1 - суретте көрсетіліп отыр.
деп белгіленген типтік кәдімгі үшбұрыш 1 - суретте көрсетіліп отыр.
1 - сурет. Есептік типтік үшбұрышты элемент.
Әрбір нүктенің ығысуының екі құраушысы болады:
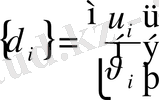 ,
,
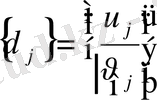 ,
,
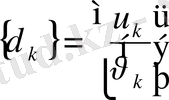 . (1)
. (1)
Ығысудың бұл алты құраушысы кез - келген
 элементі үшін мынадай вектор құрайды.
элементі үшін мынадай вектор құрайды.
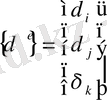 . (2)
. (2)
Суретте көрсетілгендей
 элементінің ішкі кез - келген нүктесінің ығысуы осы алты шамамен бірден - бір жолмен анықталады. Енді полиномдық функцияны таңдайық. Оның ең қарапайым түрі мынадай түрдегі сызықтық полином
элементінің ішкі кез - келген нүктесінің ығысуы осы алты шамамен бірден - бір жолмен анықталады. Енді полиномдық функцияны таңдайық. Оның ең қарапайым түрі мынадай түрдегі сызықтық полином
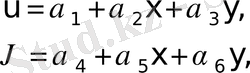 (3)
(3)
Алты тұрақты шамалар
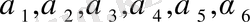 екі жүйеден оңай табылады:
екі жүйеден оңай табылады:
 -
тің орнына үшбұрыштың үш төбелерінің координаталары
-
тің орнына үшбұрыштың үш төбелерінің координаталары
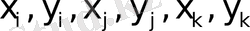 терді қойсақ онда (3) теңдеудің әрқайсысы үш теңдеуді құрайды. Олардың әрқайсысы ығысу құраушылары
терді қойсақ онда (3) теңдеудің әрқайсысы үш теңдеуді құрайды. Олардың әрқайсысы ығысу құраушылары
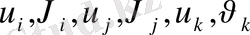 ларға тең.
ларға тең.
Мысалы:
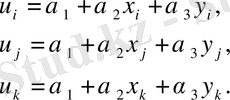 (4)
(4)
(4)
-
жүйені белгісіз коэффициенттер
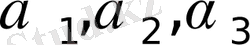 , арқылы табамыз:
, арқылы табамыз:
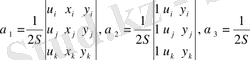
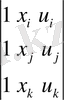 , (5)
, (5)
мұндағы
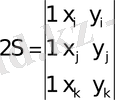 -
үшбұрыштың екі еселенген ауданы. (6)
-
үшбұрыштың екі еселенген ауданы. (6)
(5)
-
тегі анықтауыштарды ашып,
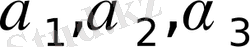 лардың мәндерін (3)
-
тің бірінші теңдеуіне қойып, мына өрнекті аламыз
лардың мәндерін (3)
-
тің бірінші теңдеуіне қойып, мына өрнекті аламыз
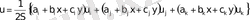 (7)
(7)
Мұндағы
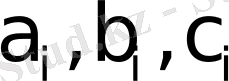 тағы басқа коэффициенттер (6) -шы анықтауышты ашу арқылы табылады және олардың мәндері мыналарға тең.
тағы басқа коэффициенттер (6) -шы анықтауышты ашу арқылы табылады және олардың мәндері мыналарға тең.
 (8)
(8)
Дәл осындай жолмен қалған алты коэффициенттер де табылады:
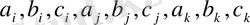 (4) - (6) амалдарды (3) - өрнектің екінші теңдеуіне қойып оларды
(4) - (6) амалдарды (3) - өрнектің екінші теңдеуіне қойып оларды
 i
,
i
,
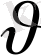 j
,
j
,
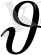 k
ларға теңестірсек (8) өрнектегі белгілеулер арқылы ығысудың
k
ларға теңестірсек (8) өрнектегі белгілеулер арқылы ығысудың
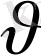 құраушысының өрнегін аламыз.
құраушысының өрнегін аламыз.
 . (9)
. (9)
Ыңғайлы болуы үшін (7) мен (9) -шы өрнектерді мына түрде жазайық
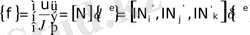 , (10)
, (10)
Мұндағы
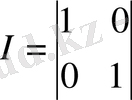 , ал
, ал
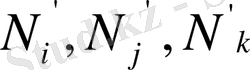 -лардың өрнектері (7) мен (9) -ды салыстыру арқылы мыналарға тең болатынын байқау қиын емес.
-лардың өрнектері (7) мен (9) -ды салыстыру арқылы мыналарға тең болатынын байқау қиын емес.
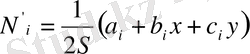 ,
,
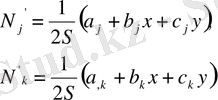 (11)
(11)
1. 3 Деформация мен кернеу өрнектері
Деформация құраушыларын серпімділік теориясындағы белгілі Кошидің геометриялық түрдегі теңдеулері арқылы жазайық.
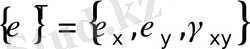 (12)
(12)
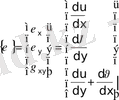 (13)
(13)
 мен
мен
 -ның (7) мен (9) -өрнектегі мәндерін (13) -ке қойып төмендегі өрнектерге келеміз.
-ның (7) мен (9) -өрнектегі мәндерін (13) -ке қойып төмендегі өрнектерге келеміз.
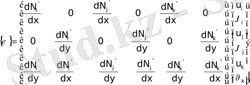 . (14)
. (14)
(11) - өрнектегі
 -лардың мәндерін (14) -ке қойсақ мынадай өрнекке келеміз.
-лардың мәндерін (14) -ке қойсақ мынадай өрнекке келеміз.
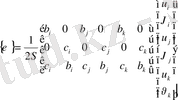 . (15)
. (15)
Бұл өрнектегі матрицаны
 деп белгілейік
деп белгілейік
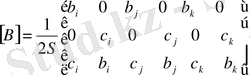 . (16)
. (16)
Сонда (15) - өрнек мына түрге келеді
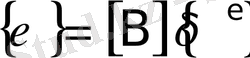 , (17)
, (17)
Мұндағы
 , (1) - (3) - өрнектегі ығысу құраушылары
, (1) - (3) - өрнектегі ығысу құраушылары
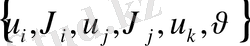 .
.
Кернеу құраушылары
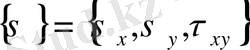 (17) - өрнектегі деформация құраушылары
(17) - өрнектегі деформация құраушылары
 арқылы мынадай өрнекпен есептеледі.
арқылы мынадай өрнекпен есептеледі.
 , (18)
, (18)
мұндағы
 - серпімділік матрицасы. Оның элементтері изотропты орта жағдайында Юнг модулі
- серпімділік матрицасы. Оның элементтері изотропты орта жағдайында Юнг модулі
 және Пуассон коэффициенті
және Пуассон коэффициенті
 арқылы құрылады. (18) өрнекті мына түрде де
арқылы құрылады. (18) өрнекті мына түрде де
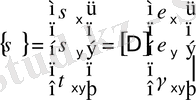 (19)
(19)
жазуға болады.
 матрицасының түзілімі жазық кернеу күйі немесе жазық деформация жағдайларына байланысты әртүрлі болады. Енді осы екі жағдайды қарастырайық.
матрицасының түзілімі жазық кернеу күйі немесе жазық деформация жағдайларына байланысты әртүрлі болады. Енді осы екі жағдайды қарастырайық.
Жазық кернеу күйі
Серпімділік теориясы курсындағы изотропты материалдар үшін деформация құраушыларын кернеу құраушылары арқылы белгілі өрнегін жазайық.
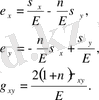 (20)
(20)
Бұл қатынастарды кернеуге қатысты шешіп
 матрицасын мына түрде аламыз.
матрицасын мына түрде аламыз.
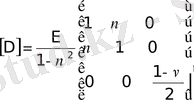 , (21)
, (21)
Түсініктірек болуы үшін (20) - ды мына түрде жазып
 -ті белгілі деп есептеп, шешіп
-ті белгілі деп есептеп, шешіп
 ті тапсақ
ті тапсақ
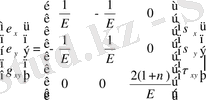 (22)
(22)
(21) өрнектің қалай шыққанын білуге болады.
Жазық деформация
Дәл осындай жолдармен жазық деформация үшін серпімділік матрицасының түрі мынадай екенін де шығарып алуға болады.
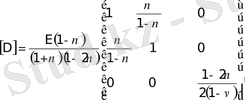 . (23)
. (23)
1. 4. Элементтің және жүйенің қатаңдық матрицаларын құру
алгоритмдері
Элементтің қатаңдық матрицасы
Сызықты
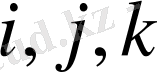 төбелері бар үшбұрышты
төбелері бар үшбұрышты
 элементті пайдаланғанда оның қатаңдық матрицасы шекті элементтер әдісінде мынадай интегралмен есептеледі.
элементті пайдаланғанда оның қатаңдық матрицасы шекті элементтер әдісінде мынадай интегралмен есептеледі.
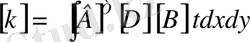 , (24)
, (24)
мұндағы
 - элементтің қалыңдығы, ал интегралдау үшбұрыштың ауданы бойынша жүргізіледі. Егер элементтің қалыңдығы тұрақты десек, бұлай деу оның өлшемдері неғұрлым кіші болса солғұрлым шындыққа жақын, онда жоғарыдағы матрицалардың бірде - біреуінде
- элементтің қалыңдығы, ал интегралдау үшбұрыштың ауданы бойынша жүргізіледі. Егер элементтің қалыңдығы тұрақты десек, бұлай деу оның өлшемдері неғұрлым кіші болса солғұрлым шындыққа жақын, онда жоғарыдағы матрицалардың бірде - біреуінде
 немесе
немесе
 айнымалысы жоқ. Олай болса (24) өрнектегі интеграл астындағы шама тұрақты ретінде интегралдан шығып мынадай өрнекке тең болады.
айнымалысы жоқ. Олай болса (24) өрнектегі интеграл астындағы шама тұрақты ретінде интегралдан шығып мынадай өрнекке тең болады.
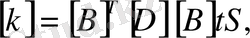 (25)
(25)
мұндағы
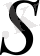 үшбұрыштың ауданы. Ол (6) -өрнекпен есептелінеді.
үшбұрыштың ауданы. Ол (6) -өрнекпен есептелінеді.
Енді (25) - өрнекке (16) -өрнектегі
 мен (23) - өрнектердегі
мен (23) - өрнектердегі
 - ның мәндерін қойсақ онда элементтің қатаңдық матрицасы үшін мынадай өрнекті аламыз.
- ның мәндерін қойсақ онда элементтің қатаңдық матрицасы үшін мынадай өрнекті аламыз.
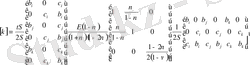 (26)
(26)
Егер элементтің қалыңдығын бірлік өлшемді болса яғни
 онда үш матрицаның алдындағы коэффициент
онда үш матрицаның алдындағы коэффициент
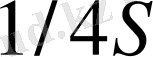 болатынын байқау қиын емес. Сонымен 6х3, 3х3 ж2не 3х6 матрицаларын көбейткендегі қортынды матрица элементтің қатаңдық матрицасы деп аталады да оның өлшемдері 6х6 болады. Яғни оның түзілімі төмендегідей
болатынын байқау қиын емес. Сонымен 6х3, 3х3 ж2не 3х6 матрицаларын көбейткендегі қортынды матрица элементтің қатаңдық матрицасы деп аталады да оның өлшемдері 6х6 болады. Яғни оның түзілімі төмендегідей
Қорыта айтқанда элементтің қатаңдық матрицасын құру үшін үшбұрыштың үш төбесінің координаталары
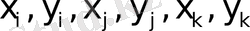 арқылы аудан
арқылы аудан
 (6) - өрнек арқылы есептеліп, (16), (24) - арқылы градиенттік және серпімділік матрицалары есептеліп (26) өрнек арқылы элементтің қатаңдық матрицасы құрылады, нәтижесі (27) өрнек түрінде жазылады. Программа осы қадамдарға құрылады.
(6) - өрнек арқылы есептеліп, (16), (24) - арқылы градиенттік және серпімділік матрицалары есептеліп (26) өрнек арқылы элементтің қатаңдық матрицасы құрылады, нәтижесі (27) өрнек түрінде жазылады. Программа осы қадамдарға құрылады.
 (27)
(27)
Жүйенің қатаңдық матрицасы
Төменде 2 - суретте жазықтықтағы есептік облысты шекті элементтер жүйесіне бөлуден үзінді көрсетілген. Егер де облысымыз тек осы 6 нүктеден ғана тұрады десек әрбір нүктенің жазықта екі еркіндік дәрежесі болатындықтан (
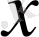 және
және
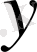 өстері бойынша) бұл жүйенің қатаңдық матрицасының реті 12 болады. Яғни алгебралық теңдеулер жүйесінің негізгі матрицасы болып табылатын қатаңдық матрицасының реті 12х12 болады.
өстері бойынша) бұл жүйенің қатаңдық матрицасының реті 12 болады. Яғни алгебралық теңдеулер жүйесінің негізгі матрицасы болып табылатын қатаңдық матрицасының реті 12х12 болады.
Жүйенің қатаңдық матрицасы элементтердің қатаңдық матрицаларының қосындыларынан құралады. Сонда оның өрнегін мына түрде жазуға болады.
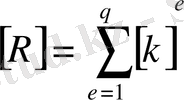 , (28)
, (28)
мұндағы
 екінші сурет бойынша беске тең, яғни
екінші сурет бойынша беске тең, яғни
 . Енді шекті элементтер әдісінің негізгі теңдеуі болып табылатын алгебралық теңдеулер жүйесін мына түрде жазуымызға болады.
. Енді шекті элементтер әдісінің негізгі теңдеуі болып табылатын алгебралық теңдеулер жүйесін мына түрде жазуымызға болады.
 ,
,
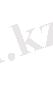 (29)
(29)
мұндағы
 - жүйенің қатаңдық матрицасы, жалпы жағдайдағы оның өлшемі 2n*2n;
- жүйенің қатаңдық матрицасы, жалпы жағдайдағы оның өлшемі 2n*2n;
 ,
,
 - белгісіз ығысу құраушылары мен белгілі сыртқы немесе көлемдік күш векторлары, өлшемі - 2*n. Мұндағы
- белгісіз ығысу құраушылары мен белгілі сыртқы немесе көлемдік күш векторлары, өлшемі - 2*n. Мұндағы
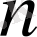 есептік облыстағы нүктелердің жалпы саны.
есептік облыстағы нүктелердің жалпы саны.
2 - сурет. Жазықтағы шекті элементтер жүйесінен фрагмент.
II - Бөлім ЭЛЕМЕНТ ПЕН ЖҮЙЕНІҢ ҚАТАҢДЫҚ МАТРИЦАЛАРЫН
ІС ЖҮЗІНДЕ ҚҰРУ
2. 1 Жүйенің қатаңдық матрицасын құрылымы туралы
Шекті элементтер әдісінде жүйенің қатаңдық матрицасының құрылымы зерттеу облысын элементтерге бөлу түріне, әсіресе олардың төбелерін нөмірлеу түріне байланысты. Жалпы жағдайда жүйенің қатаңдық матрицасы квадратты және симметриялы болады. Егер элементтердің төбелерін ерекше жолмен ықшамдап нөмірлей білсек, онда толық матрицаның орнына (3 - сурет) диагональ маңайында симметриялық (4 - сурет) немесе диагоналдық симметриялық және ленталық (5 - сурет) етіп құруға болады.

3 - сурет. Толық матрица кескіні

4 - сурет. Симметриялық басым диагоналдық матрица кескіні

5 - сурет. Симметриялық ленталық матрица кескіні
Жүйенің қатаңдық матрицасын 4 -ші немесе 5 - суреттердегідей етіп құрудың үлкен мәнісі бар. Қазіргі заманғы компьютерлердің оперативтік жадысы мен тактылық жиілігі қаншама жоғарылап келе жатқанымен кеңістіктік есептер, әсіресе кеңістіктік динамикалық есептерді уақыттың дискретті мәндері үшін шешуге ең соңғы, ең қуатты компьютердің де мүмкіндігі жоқ. Қатаңдық матрицасын диагоналдық симметриялық етіп құрғанда оның нөл емес элементтері диагональ маңайына топтасады да жалпы санынан екү, үш, бес, он, елу, жүз есеге дейін кемиді. Компьютер жадысында квадраттық матрица орнына 6 - суретте көрсетілгендей тік матрица түрінде диагоналдың тек астыңғы немесе үстіңгі жақтарының элементтері ғана сақталады. 5 - суреттегі диагональ маңайындағы нөл емес элементтердің ең үлкен санын яғни енін алдын - ала білуге болады. Ол еннің ішінде азын - аулақ нөл сндары болады. Оны алдағы мысалдарда толық көрсетеміз.
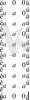
6 - сурет тік бұрыш түріндегі диагоналдың үстіңгі элементтерінен құрылған матрица
Енді нақты мысалдармен элемент пен жүйенің қатаңдық матрицаларын құрайық. Шардара, Қапшағай, Бұқтарма тағы басқа су үлкен су қоймаларына салынады. Ағып жатқан өзен арнасын бөгеу үшін тау жыныстарымен топырақтан үйіп, бөгет жасайды. Бөгеттің пішінінің көлденең көлденең қимасының кескіні геометриялық тұрғыдан трапеция тәрізді болып келеді. Алғаш салынған автомобиль немесе поезд жолын салу үшін де алдымен топырақ немесе тау жынысын трапеция тәрізді етіп үйеді. Бөгеттің көлденең қимасының трапециялық кескіні 7 - суретте көрсетілгендегідей дейік.
6 - сурет. Зерттеу облысының көлденең қимасының кескіні
Осы облысты алдымен үшбұрышты екі элементке бөліп оларды және олардың төбелерін цифрлармен және формуламен есептеуге келетіндей етіп
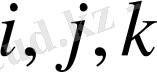 деп нөмірлейік (7 - сурет) .
деп нөмірлейік (7 - сурет) .
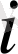
7 - сурет. Зерттеу облысын екі элементке бөліп нөмірлеу
Айта кететін нәрсе
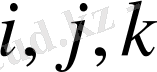 -ны үнемі сағат тілінің бағытымен немесе үнемі оған қарсы бағытта ұстау керек. Мысалы бір есеп көлемінде бірде
-ны үнемі сағат тілінің бағытымен немесе үнемі оған қарсы бағытта ұстау керек. Мысалы бір есеп көлемінде бірде
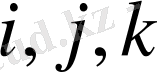 және
және
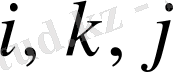 деуге болмайды, бiрақ
деуге болмайды, бiрақ
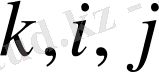 немесе
немесе
 деп аралас қолдана беруге болады. Алдымен суреттегі дөңгелек ішінде 1-деп нөмірленген элементті қарастырайық. Оның қатаңдық матрицасының өлшемі 6х6 болатыны I-бөлімде айтылды. Есептік облыста барлығы 4 нүкте бар. Жүйенің қатаңдық матрицасының өлшемі жазық есептерде
деп аралас қолдана беруге болады. Алдымен суреттегі дөңгелек ішінде 1-деп нөмірленген элементті қарастырайық. Оның қатаңдық матрицасының өлшемі 6х6 болатыны I-бөлімде айтылды. Есептік облыста барлығы 4 нүкте бар. Жүйенің қатаңдық матрицасының өлшемі жазық есептерде
 болатыны айтылды (
болатыны айтылды (
 есептік облыстағы нүктелердің саны) . Демек 7 - суретте көрсетілген облыс үшін екi элементтiң қатаңдық матрицаларынан құралатын жүйенiң қатаңдық матрицасының өлшемi 8х8 болады
есептік облыстағы нүктелердің саны) . Демек 7 - суретте көрсетілген облыс үшін екi элементтiң қатаңдық матрицаларынан құралатын жүйенiң қатаңдық матрицасының өлшемi 8х8 болады
Ендi (136), (137) -шi формулалар бойынша кез - келген үшбұрыштың төбелерiнiң нөмiрлерiне сәйкес келетiн жүйенiң қатаңдық матрицасының жатық және тiк жолдарының нөмiрлерiн табу өрнектерiн жазайық. Шектi элементтермен айналысып, бiрақ оны игере алмаушылардың түсiнбейтiнi дәл осы мәселе. Бұл өрнектердiң мән, мағынасын түсiнбеген жағдайда әрi қарай жылжу болмайды! С. Б. Уховтың (Расчет сооружений и основании методом конечных элементов, М., 1973) оқулығынан басқа шектi өлементтерге арналған бiрде - бiр оқулықта тәптiштеп түсiндiрiлмейдi. Л. Сегерлиндтiң Л. (Применение метода конечных элементов. - М. : Недра, 1979) тамаша оқулығы бойынша да пайдаланушының өз бетiмен түсiнiп кетуi қиын .
Бұл жерде баяндалатын әдiс С. Б. Ухов оқулығындағыдан мүлдем басқаша. Үшбұрыштың 3 төбесiнiң әрқайсысының
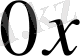 және
және
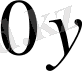 өстерiнiң бағыттарында ығысудың екi құраушысы болатындықтан барлығы 6 теңдеу болады. Сонымен элементтiң қатаңдық матрицасы мен жүйенiң қатаңдық матрицасының элементтерiн байланыстыратын формуланың түрi
өстерiнiң бағыттарында ығысудың екi құраушысы болатындықтан барлығы 6 теңдеу болады. Сонымен элементтiң қатаңдық матрицасы мен жүйенiң қатаңдық матрицасының элементтерiн байланыстыратын формуланың түрi
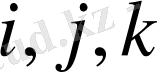 арқылы былай жазылады.
арқылы былай жазылады.
;
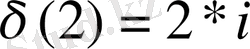 ;
;
; (30)
;
;
.
Бұл формулалардың қызметiн түсiнбеген адам шектi элементтер әдiсiн ешуақытта да түсiне алмайды! Сондықтан бұл оқулықтағы ең қиын мәселені егжей - тегжейлi баяндайық. Ол үшiн 7 -суреттегi 1-8ші бұрышты 8-сурет түрiнде жеке бөліп қарастырайық. Оның
 төбесінің ығысуын
төбесінің ығысуын
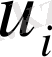 құраушысына (30) теңдеудегі
құраушысына (30) теңдеудегі
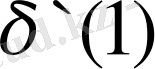 ,
,
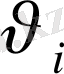 құраушысына
құраушысына
 құраушысы сәйкес келеді. Сол сияқты
құраушысы сәйкес келеді. Сол сияқты
 мен
мен
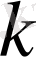 төбелерінің әрқайсысының
төбелерінің әрқайсысының
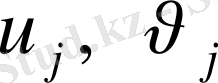 құраушыларына (30) теңдеудің
құраушыларына (30) теңдеудің
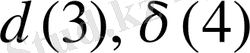 және
және
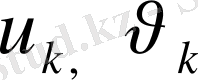 төбелеріне
төбелеріне
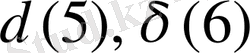 өрнектері сәйкес келеді. Үш төбеге түсетін сыртқы немесе ішкі күштің 6 құраушылары да дәл осы жолмен анықталады.
өрнектері сәйкес келеді. Үш төбеге түсетін сыртқы немесе ішкі күштің 6 құраушылары да дәл осы жолмен анықталады.
8 - сурет. Үшбұрышты элементтiң жалпы және жергiлiктi нөмiрлерi
Олай болса
;
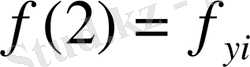 ;
;
; (31)
;
;
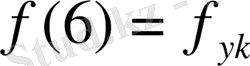 .
.
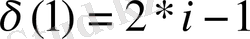 (32)
(32)
Енді 6-суреттегі нақты элементтің яғни 1-шi элементтiң жергілікті
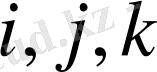 нөмiрлерiн жалпы нөмірімен байланысын (30) бойынша жазайық. Бұл жерде
нөмiрлерiн жалпы нөмірімен байланысын (30) бойынша жазайық. Бұл жерде
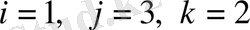
Екеніне көңіл бөлу керек. Элементтiң қалыңдығы
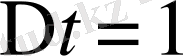 , төрт төбесіндегі нүктелердiң координаталары
, төрт төбесіндегі нүктелердiң координаталары
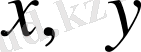 ті тағайындап, материалдың серпiмдiлiк қасиеттерi белгiлi деп (
ті тағайындап, материалдың серпiмдiлiк қасиеттерi белгiлi деп (
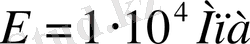 ,
,
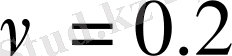 ) (24) өрнек бойынша үш матрицаның көбейтiндiсiмен элементтiң қатаңдық матрицасын құрамыз. Ол матрицаларды көбейту нәтижесінде алынған
) (24) өрнек бойынша үш матрицаның көбейтiндiсiмен элементтiң қатаңдық матрицасын құрамыз. Ол матрицаларды көбейту нәтижесінде алынған
 матрицасының өлшемі 6х6 болады. Ендi осы матрицаны жергiлiктi және жалпы нөмiрлер арқылы жазайық.
матрицасының өлшемі 6х6 болады. Ендi осы матрицаны жергiлiктi және жалпы нөмiрлер арқылы жазайық.
Жергiлiктi нөмiр
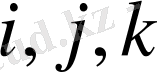 бойынша
бойынша
 (33)
(33)
Жалпы нөмiрi 1, 3, 2 бойынша

. (34)
Соңғы екi өрнектің оң қараңыз. Программалау үшін цикл құруға бір идентификатормен белгілеу әлдеқайда қолайлы, сондықтан бұл жерде мынадай өзара тең ауыстырулар пайдаланылып отыр.
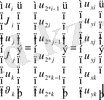 (35)
(35)
Алдағы баяндауларда немесе шекті элементтерге арналған өзге авторлардың кітаптарында осындай үш түрлі белгілеулер қолданылады. Түсінікті болуы, әрі есте қалуы үшін (35) өрнекті арнайы жазып, көңіл аударып отырмыз, Мысалы жоғарыдағы (33) өрнектегі
 пен
пен
 -ға (35) өрнек аралас өолданылып отырғанына назар аударыңыз.
-ға (35) өрнек аралас өолданылып отырғанына назар аударыңыз.
Енді (34) - өрнекті өлшемі (21) -сурет бойынша 8х8 екенi алдын-ала белгiлi жүйенiң қатаңдық матрицасына жiберейiк.
2. 2 Жүйенің қатаңдық матрицасын құрудың басты ережесі
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz