Алгебралық теңдеулер жүйесін шешудің классикалық және дамыған әдістері


МАЗМҰНЫ
Кіріспе 4
I - Бөлім АЛГЕБРАЛЫҚ ТЕҢДЕУЛЕР ЖҮЙЕСІН
ШЕШУДІҢ КЛАССИКАЛЫҚ ӘДІСТЕРІ . . 5
1. 1. Негізгі ұғымдар және анықтамалар . . . 5
1. 2 Крамер формуласы . . . 6
1. 3 Жалпы түрдегі алгебралық теңдеулер жүйесін шешу жолы …… . . . 9
1. 4 Гаусс әдісі. 12
II - Бөлім АЛГЕБРАЛЫҚ ТЕҢДЕУЛЕР ЖҮЙЕСІН
ШЕШУДІҢ ДАМЫҒАН ӘДІСТЕРІ . . . 17
2. 1 Кері матрица әдісі17
2. 2 Біртекті алгебралық теңдеулер жүйесі . . . 18
2. 3 Сызықты теңдеулер жүйесін шешудің итерациялық әдістері . . . 20
2. 4 Теңдеулер жүйесін шешудің түйіндес градиенттік әдісі . . . 22
2. 5 Теңдеулер жүйесін шешудің Холецкий әдісі . . . 24
Қортынды. 33
Пайдаланылған әдебиеттер. 34
КІРІСПЕ
Мектеп программасында сызықты алгебралық теңдеулердің үшінші, төртінші ретке дейінгілері Гаусс әдісімен, ал екінші, үшінші ретке дейінгілері Крамер әдісімен үйретіледі. Себебі Крамер әдісінде есептеу өрнектері тым көбейіп кетеді. Мысалы төртінші ретті матрицаны үшінші ретке түсіріп бір жүйе құру керек. Одан соң оны үшбұрыштар әдісімен шешу керек. Егер бесінші ретті теңдеулер жүйесі берілсе онда оған Крамер әдісін принципінде қолдануға болатынымен іс жүзінде қолдану өте тиімсіз, себебі тым көп есептеулер жүргізуге тура келеді де ұзаққа созылып кетеді.
Аталған бұл екі әдісті бірінші бөлімге топтастырдық да екінші бөлімге жоғары математика курсында өтілетін «Кері матрица әдісі», «Итерациялық әдістер», «Түйіндес градиенттік әдіс», «Холецкий әдісі» секілді әдістерді классикалық әдістердің дамытылған түрлері ретінде екінші бөлімге топтастырдық.
Әрбір бөлім мен тақырыптардың соңында нақты есептер мен мысалдар келтіріліп, арнайы тапсырмалар жинағын ұсынуға көңіл бөлінді.
I - Бөлім АЛГЕБРАЛЫҚ ТЕҢДЕУЛЕР ЖҮЙЕСІН ШЕШУДІҢ КЛАССИКАЛЫҚ ӘДІСТЕРІ
1. 1 Негізгі ұғымдар және анықтамалар
Алгебралық сызықты теңдеулер жүйесі арқылы көптеген экономикалық есептер шығарылады.
n -белгісізі бар m теңдеулер жүйесі былай жазылады:
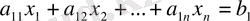 ,
,
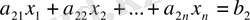 , (56)
, (56)
. .
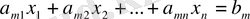
Мұнда а
ij
, в
j
(i=1, 2, . ., m, j=1, 2, . ., n) -нақты сандар, а
ij
-жүйенің коэффициенті, ал в
j
-бос мүшесі деп аталады. Коэффициенттің бірінші индексі i-теңдеудің номеріне, ал екінші j- белгісіздің номеріне сәйкес келеді. (56) -інші жүйе қысқа түрде
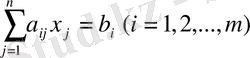
Егер
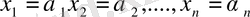 сандар тобын (56) жүйесіндегі
сандар тобын (56) жүйесіндегі
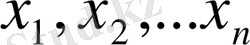 белгісіздерінің орнына қойсақ әрбір теңдеу тепе-теңдікке айналатын болса, онда
белгісіздерінің орнына қойсақ әрбір теңдеу тепе-теңдікке айналатын болса, онда
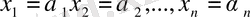 - тобы (56) жүйесінің шешімі деп аталады. Ең болмағанда бір шешімі бар жүйе үйлесімді жүйе деп аталады. Ал егер жүйенің бірде бір шешімі жоқ болса, онда ол үйлесімсіз жүйе деп аталады. Үйлесімді жүйенің тек бір ғана шешімі бар болса, онда ол анықталған жүйе деп, ал бірден көп шешімі бар болса анықталмаған жүйе деп аталады.
- тобы (56) жүйесінің шешімі деп аталады. Ең болмағанда бір шешімі бар жүйе үйлесімді жүйе деп аталады. Ал егер жүйенің бірде бір шешімі жоқ болса, онда ол үйлесімсіз жүйе деп аталады. Үйлесімді жүйенің тек бір ғана шешімі бар болса, онда ол анықталған жүйе деп, ал бірден көп шешімі бар болса анықталмаған жүйе деп аталады.
Мысалы:
анықталған жүйе, өйткені оның бір ғана
шешімі
бар (5; 0), ал
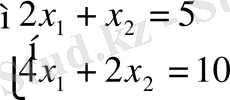 үйлесімді, бірақ анықталмаған жүйе, өйткені
үйлесімді, бірақ анықталмаған жүйе, өйткені
оның бірден көп шешімі бар: х 1 =С 1 , х 2 =5-2 С 1 немесе (С 1 , 5-2 С 1 ) . Мұндағы С 1 -кез-келген сан.
Егерде екі жүйенің шешімдері біодей болса, онда оңай жүйелер эквивалентті жүйелер деп аталады. (56) жүйесін матрицалық түрде жазуға болады:
[А] Х=[В] (57)
Мұндағы
 (56)
(56)
жүйесінің матрицасы
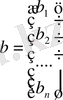 тік жолды бос мүше матрицасы, ал
тік жолды бос мүше матрицасы, ал
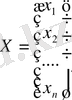
белгісіздердің тік жолды матрицасы.
1. 2 Крамер теоремасы
Егер ∆≠0 болса, онда (58) теңдеулер жүйесі жинақты және анықталған жүйе болады. Бұл жүйенің жалғыз шешімі
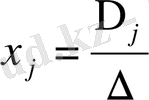
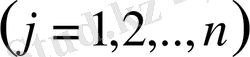 (59)
(59)
формуласымен анықталады.
Дәлелдеуі: Кері матрица әдісінің (60) формуласымен ашып жазамыз.

Теңдіктің оң жағындағы екі матрицаны көбейту амалын орындап, екі матрицанын теңдігінің анықтамасын қолданатын болсақ, онда белгісіздерді анықтайтын
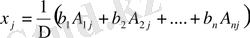
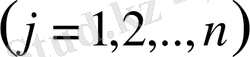 формуласын аламыз. Лаплас теоремасы (1. 3-інші тақырып) бойынша жақшаның ішіндегі қосынды
формуласын аламыз. Лаплас теоремасы (1. 3-інші тақырып) бойынша жақшаның ішіндегі қосынды
 анықтауышына тең. Сондықтан соңғы формуладан (61) формуласы Крамер формуласы деп аталады.
анықтауышына тең. Сондықтан соңғы формуладан (61) формуласы Крамер формуласы деп аталады.
Мысал
:
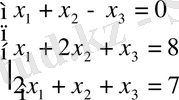
жүйесін
а) кері матрица әдісімен және
б) Крамер формуласын қолданып шешіңіз.
Шешуі : а) Жүйенің матрицасын, бос мүшелер және белгісіздер
матрицаларын құрамыз:
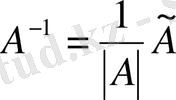
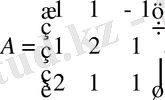
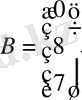
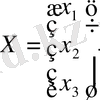
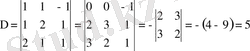
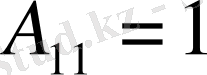

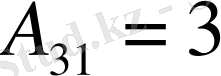
.
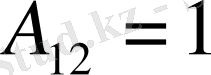
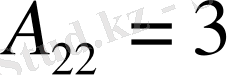


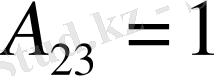
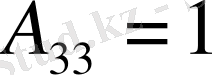
[А] матрицасы элементтерінің алгебралық толықтауыштарын таптық.
Сондықтан (10) формуласы бойынша
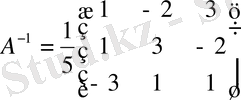 Енді (60)
Енді (60)
формуласын қолданамыз:
 .
.
Сонымен жүйенің шешімі (1, 2, 3) .
б)
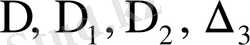 анықтауыштарын есептейміз.
анықтауыштарын есептейміз.
 ,
,
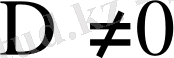 болғандықтан Крамер теоремасы бойынша жүйенің тек бір шешімі бар.
болғандықтан Крамер теоремасы бойынша жүйенің тек бір шешімі бар.
 анықтауышы
анықтауышы
 -дан бірінші тік жолды бос мүшенің тік жолымен ауыстырғанда шығады.
-дан бірінші тік жолды бос мүшенің тік жолымен ауыстырғанда шығады.
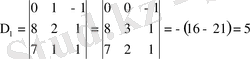
 анықтауышының екінші жолын бос мүшенің тік жолымен ауыстырсақ
анықтауышының екінші жолын бос мүшенің тік жолымен ауыстырсақ
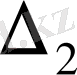 анықтауышы шығады.
анықтауышы шығады.
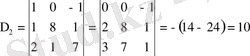
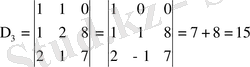
Крамер формуласы бойынша
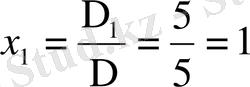
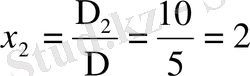
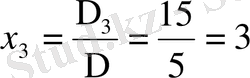
Жүйенің шешімі (1, 2, 3) .
Егер (57) теңдеуіне А, Х және В матрицаларының мәндерін қойып және екі матрицаны көбейту амалын орындайтын болсақ, онда
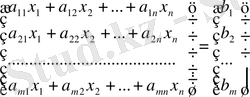 теңдігі шығады.
теңдігі шығады.
1. 3 Жалпы түріндегі алгебралық теңдеулер жүйесінің түзілімі
n белгісізі бар m теңдеулер жүйесін, яғни (56) теңдеулер жүйесін қарастырайық. Матрицаның рангісін оның сызықтық байланысты емес жатық жолдарының ең үлкен санына тең. Сондықтан, егер кеңейтілген А 1 матрицасының жатық жолдары, яғни жүйенің теңдеулер сызықтық байланыссыз болса, онда [А] 1 матрицасының рангісін теңдеулер санына тең болады: r=m, ал егер сызықтық байланысты болса, онда r<m. (56) теңдеулер жүйесінің үйлесімділігін анықтайтын негізгі теореманы дәлелдеу керек.
Кронекер-Капелла теоремасы.
Алгебралық сызықты теңдеулер жүйесінің үйлесімді болуы үшін матрицасы мен кеңейтілген матрицасының рангітері өзара тең, яғни
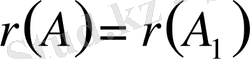 болу қажетті және жеткілікті.
болу қажетті және жеткілікті.
Үйлесімді алгебралық сызықты теңдеулер жүйесі үшін төмендегі тұжырымдар орындалады.
- егер үйлесімді (56) жүйе матрицасының рангісі белгісіздер санынан кем, яғни r=n болса, онда (56) жүйесі анықталған жүйе болады.
- егер үйлесімді (56) жүйе матрицаның рангісі белгісіздер санынан кем, яғни r<n болса, онда (56) жүйесі анықталмаған жүйе болады және оның шексіз көп шешімі бар.
r<n теңсіздігі орындалсын. Егер х 1 , х 2 , …, х r белгісіздердің алдында тұрған коэффициенттерден құрылған анықтауыш (базистік минор) нөлге тең болса, онда х 1 , х 2 , …, х r белгісіздері базистік белгісіздер деп, ал қалған n- r белгісіздер бос белгісіздер деп аталады.
(56) жүйесінің барлық n- r бос белгісіздері нөлге тең болатын шешімі базистік шешім деп аталады. (56) жүйесі үйлесімді және оның рангісі r болсын. Жүйенің матрицасының бір базистік минорды, яғни реті r-ге тең r-ге тең, бірақ өзі нөлге тең емес минорды қарастырамыз. Мысалға А мен А 1 матрицаларының алғашқы r жатық жолы базистік жатық жолдар арқылы сызықты өрнектеледі, сондықтан (56) жүйесінің соңғы m- r теңдеулері алғашқы r теңдеулер арқылы сызықты өрнектелетін болғандықтан, оларды жүйенің құрамынан алып тастаймыз.
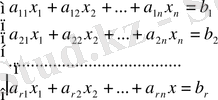 (62)
(62)
жүйесінің рангісі теңдеулер санына тең емес r≤n. сондықтан екі жағдай болуы мүмкін: не r=n, не r<n.
Бірінші жағдайда жүйенің матрицасы шаршылы және айырықша емес, сондықтан Крамер теоремасы бойынша ол анықталған үйлесімді жүйе.
Енді r<n болсын. Теңдіктердің оң жағынан бос белгісіздері бар
мүшелерді шығарамыз.
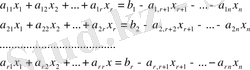 (63)
(63)
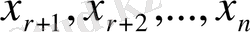 белгісіздеріне кез-келген мәні болады, сондықтан олар бос белгісіздер деп аталады. Крамер теоремасы бойынша (63) жүйесіндегі
белгісіздеріне кез-келген мәні болады, сондықтан олар бос белгісіздер деп аталады. Крамер теоремасы бойынша (63) жүйесіндегі
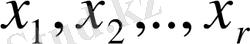 белгісіздерін қалған бос белгісіздер бойынша табуға болады. бос белгісіздер кез-келген мән қабылдай алатындықтан r<n болған жағдайда (56) жүйесі үйлесімді, бірақ анықталмаған жүйе.
белгісіздерін қалған бос белгісіздер бойынша табуға болады. бос белгісіздер кез-келген мән қабылдай алатындықтан r<n болған жағдайда (56) жүйесі үйлесімді, бірақ анықталмаған жүйе.
Мысал:
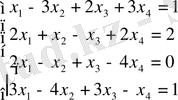 жүйесі берілсін.
жүйесі берілсін.
а) жүйенің үйлесімділігін тексеріңіз.
б) жүйенің шешімдерін табыңыз.
Шешуі: а) Жүйенің матрицасы мен кеңейтілген матрицасының
рангілерін табамыз.
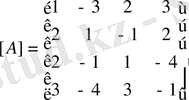 [А] матрицасының рангісін
[А] матрицасының рангісін
көмкекруші минорлар әдісімен табамыз.

4-ші ретті жалғыз минор нөлге тең болады. Сондықтан нөлге тең емес 3-ші ретті минор бар болғандықтан
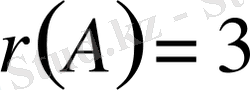 . Нөлге тең емес осы минор кеңейтілген [А]
1
матрицасының да құрамына кіретін болғандықтан біз [А]
1
матрицасының 4-ші ретті минорларды тексереміз. Нөлге тең емес 3-ші ретті минорды көмкеретін 4-ші ретті екі минордың біреуінің нөлге теңдігін көрдік. Енді екінші минорды тексереміз.
. Нөлге тең емес осы минор кеңейтілген [А]
1
матрицасының да құрамына кіретін болғандықтан біз [А]
1
матрицасының 4-ші ретті минорларды тексереміз. Нөлге тең емес 3-ші ретті минорды көмкеретін 4-ші ретті екі минордың біреуінің нөлге теңдігін көрдік. Енді екінші минорды тексереміз.
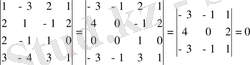 .
.
Сондықтан
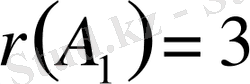 Олай болса Кронекер-Капелла теоремасы бойынша берілген жүйе үйлесімді.
Олай болса Кронекер-Капелла теоремасы бойынша берілген жүйе үйлесімді.
б) алдында тұрған коэффициенттері базистік минорды құратын болғандықтан
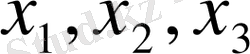 белгісіздері базистік белгісіздер, ал
белгісіздері базистік белгісіздер, ал
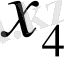 -бос белгісіз болады. Төртінші теңдеудің коэффмцменттері базистік минордың элементтері болмайды, сондықтан төртінші теңдеу басқа теңдеулердің сызықтық өрнегі болады. Дәлірек айтсақ, 4-ші теңдеу 1-ші теңдеу мен 3-ші теңдеулердің қосындысы. Сондықтан 4-інші теңдеуді жүйенің құрамынан алып тастап, қалған теңдеулерді
-бос белгісіз болады. Төртінші теңдеудің коэффмцменттері базистік минордың элементтері болмайды, сондықтан төртінші теңдеу басқа теңдеулердің сызықтық өрнегі болады. Дәлірек айтсақ, 4-ші теңдеу 1-ші теңдеу мен 3-ші теңдеулердің қосындысы. Сондықтан 4-інші теңдеуді жүйенің құрамынан алып тастап, қалған теңдеулерді
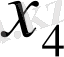 белгісізі бар мүшелерді теңдеулердің оң жағына шығарамыз:
белгісізі бар мүшелерді теңдеулердің оң жағына шығарамыз:
1. 4 Гаусс әдісі
Реті
 болатын алгебралық теңдеулер жүйесін қарастырайық. Ондай жүйені шешу үшін кейде белгілі бір бөліктерге бөліп тастап барып амалдар қолданған ыңғайлы. Мысалы теңдеулер жүйесінің коэффициенттерінен құралған матрицаны 4 бөлікке бөліп тастауға болады. Жоғарғы алгебра курстарында қалыптасқан алгебралық сызықты теңдеулер жүйесін
болатын алгебралық теңдеулер жүйесін қарастырайық. Ондай жүйені шешу үшін кейде белгілі бір бөліктерге бөліп тастап барып амалдар қолданған ыңғайлы. Мысалы теңдеулер жүйесінің коэффициенттерінен құралған матрицаны 4 бөлікке бөліп тастауға болады. Жоғарғы алгебра курстарында қалыптасқан алгебралық сызықты теңдеулер жүйесін
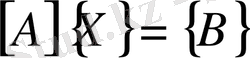 деген белгілеулер орнына шекті элементтер әдісінде қалыптасқан
деген белгілеулер орнына шекті элементтер әдісінде қалыптасқан
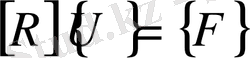 , (64)
, (64)
белгілеулерін пайдаланайық. Сонымен осы соңғы теңдеулер жүйесін төрт бөлікке бөлу түрін жазайық.
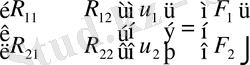 , (65)
, (65)
мұндағы
 матрицасының өлшемі
матрицасының өлшемі
 ;
;
 матрицасының өлшемі
матрицасының өлшемі
 ;
;
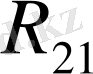 матрицасының өлшемі
матрицасының өлшемі
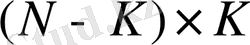 ;
;
 матрицасының өлшемі
матрицасының өлшемі
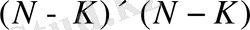 ;
;
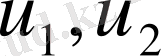 - белгісіз шамалардың векторы;
- белгісіз шамалардың векторы;
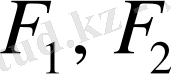 - белгілі шамалар векторы;
- белгілі шамалар векторы;
Гаусстың белгісіздерді біртіндеп «жою» әдісі
 матрицасының өлшемін кішірейтіп, оны
матрицасының өлшемін кішірейтіп, оны
 түрінде алуға мүмкіндік береді. Реті кішірейген ол матрицаны
түрінде алуға мүмкіндік береді. Реті кішірейген ол матрицаны
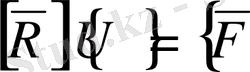 (66)
(66)
деп жазайық. Сонда бастапқы
 матрицамыз және оның оң жағы
матрицамыз және оның оң жағы
 -векторы әрқайсысының реттері төмен мынадай матрицалардың көбейтінділерімен анықталады.
-векторы әрқайсысының реттері төмен мынадай матрицалардың көбейтінділерімен анықталады.
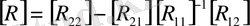 (67)
(67)
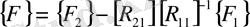 (68)
(68)
Дәл осы жолмен
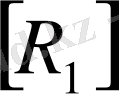 матрицасын да реті одан да кіші матрицаға жіктеуге болады. Бұл жердегі негізгі амал мынадай үш матрицаның көбейтіндісі
матрицасын да реті одан да кіші матрицаға жіктеуге болады. Бұл жердегі негізгі амал мынадай үш матрицаның көбейтіндісі
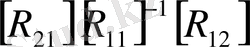 болатынын байқау қиын емес. Бұл жердегі
болатынын байқау қиын емес. Бұл жердегі
 матрицасының өлшемі
матрицасының өлшемі
 болғандықтан қолданылатын амалдардың саны
болғандықтан қолданылатын амалдардың саны
 болады. Осылай біртіндеп кішірейте отырып
болады. Осылай біртіндеп кішірейте отырып
 матрицасының өлшемін
матрицасының өлшемін
 ға дейін түсіргенде, ең соңғы
ға дейін түсіргенде, ең соңғы
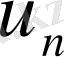 белгісізін бірден табуға болады.
белгісізін бірден табуға болады.
Одан әрі қарай біртіндеп кері қадамдар жасай отырып қалған басқа белгісіздерді де мынадай алгоритммен табуға болады
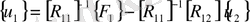 . (69)
. (69)
Бұл әдіс бастапқы
 матрицасының элементтері компьютердің оперативтік жадысында сақталатын қарапайым әдіс деп есептелінеді. Егер
матрицасының элементтері компьютердің оперативтік жадысында сақталатын қарапайым әдіс деп есептелінеді. Егер
 матрицасы симметриялы болса, онда оның тек диагоналы мен диагональ үстіндегі немесе диагональ астындағы элементтерін ғана пайдаланып орындалатын амалдарды екі есеге дейін азайтуға болады. Соңғы жағдайда
матрицасы симметриялы болса, онда оның тек диагоналы мен диагональ үстіндегі немесе диагональ астындағы элементтерін ғана пайдаланып орындалатын амалдарды екі есеге дейін азайтуға болады. Соңғы жағдайда
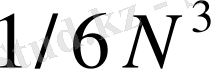 амал орындалады.
амал орындалады.
Жалпы түрде берілген (56) теңдеулер жүйесін қарамыз. Кері матрица әдісі мен Крамер формуласын белгісіздер саны мен теңдеулер саны өзара тең болғанда және жүйенің анықтауышы нольге тең болмағанда қолдануға болады. Сонымен Гаусс әдісі деп белгісіздерді біртіндеп табу әдісін айтамыз.
Жүйенің

Алгебралық теңдеулер жүйесінің коэфициенттерінен
 матрицасын құрайық.
матрицасын құрайық.
Егер элементар түрлендіруді қолдану барысында бір жатық жолдың соңғы элементінен (бос мүшеден) басқа элементтері нөл санына тең болып шықса, онда берілген жүйе үйлесімсіз жүйе болады. Бұл жағдайда жүйенің шешімін іздеуді дереу тоқтатамыз. Егерде элементар түрлендіру кезінде нөлдерден тұратын жатық жол шықса, ол жатық жолды элементар түрлендірудің анықтамасы бойынша матрица құрамынан алып тастаймыз. Кеңейтілген матрицаны сатылы түрге келтірілгеннен кейін, ол арқылы теңдеулер жүйесін құрамыз. Осы теңдеулер жүйесін соңғы теңдеуінен бастап бір-бірлеп шешеміз, яғни бір белгісіз деп басқасын белгілі деп жариялап, белгісіз айнымалыны белгілі айнымалылар арқылы өрнектейміз. Табылған белгісіздерді келесі жоғарғы тұрған теңдеуге қойып, келесі белгісізді таба аламыз. Осы процесті бірінші теңдеуге дейін жеткізіп, барлық белгісіздерді анықтаймыз. Енді Гаусс әдісін қолданып есеп шығарсақ.
Мысал:
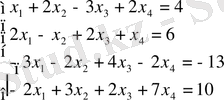
теңдеулерін Гаусс әдісімен шешіңіз.
Дәлелдеуі : Жүйенің кеңейтілген матрицасын құрамыз.

мұнда есептеуге ыңғайлы болу үшін бос
мүшенің бағанасы басқа тік жолдардан түзу арқылы бөлініп тұр. Бірінші тік жолдың 2-інші, 3-інші және 4-інші элементтерін нөл жасау үшін бірінші жатық жолды 2-ге көбейтіп 2-ші жатық жолға, 3-ке көбейтіп 3-інші жатық жолға және 2-інші жатық жолды 4-інші жатық жолға қосамыз.
 соңғы матрицадан екінші
соңғы матрицадан екінші
жатық жолға үшінші жатық жолды, ал үшінші жатық -2-ге көбейтілген төртінші жатық жолды қосамыз, сонан соң төртінші жатық жолды 2-ге бөлеміз.
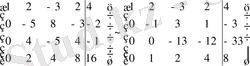
Енді төртінші жатық жолға екінші жолды қосып, сонан соң үшінші жатық жол мен төртінші жатық жолдардың орындарын ауыстырып жазамыз.
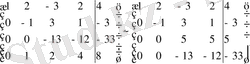
Үшінші жатық жолды 5-ке бөліп жазамыз, сонаң соң оны 13-ке көбейтіп 4-інші жатық жолға қосамыз.
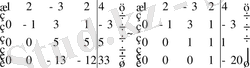
жүйенің кеңейтілген матрицасын баспалдақ түрге келтірдік. Енді осы матрица бойынша теңдеулер жүйесін қалпына келтіреміз:
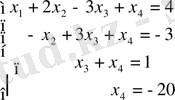
Соңғы екі теңдеуден
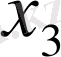 пен
пен
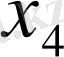 -ті тауып, екінші теңдеуге қосамыз.
-ті тауып, екінші теңдеуге қосамыз.
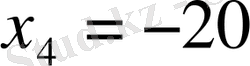 ,
,

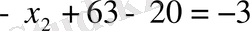

Табылған
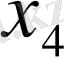
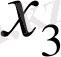
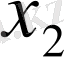 -лердің мәндерін бірінші теңдеуге қойып,
-лердің мәндерін бірінші теңдеуге қойып,
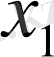 -дің мәнін табамыз:
-дің мәнін табамыз:
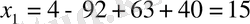 (15, 46, 21, -20)
(15, 46, 21, -20)
Мысал: Гаусс әдісі бойынша шешіңіз.
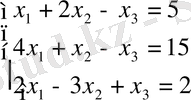
Шешуі
:
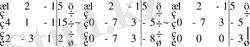
Соңғы жатық
жол бойынша теңдеуі құратын болсақ
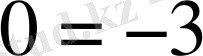 шығады. Соңдықтан берілген жүйе үйлесімсіз, яғни оның шешімі жоқ.
шығады. Соңдықтан берілген жүйе үйлесімсіз, яғни оның шешімі жоқ.
Мысал
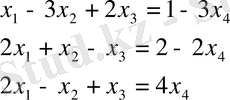
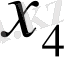 -ке кез-келген мәнін беріп (
-ке кез-келген мәнін беріп (
 ), соңғы жүйені
), соңғы жүйені
Гаусс әдісімен шешеміз:
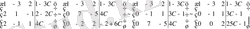
соңғы матрица бойынша жүйе құрамыз:
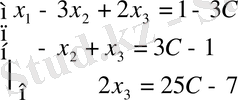
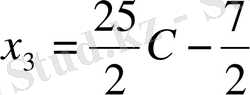
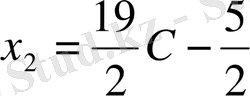
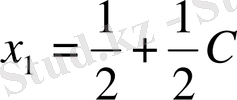 С кез-келген сан болғандықтан,
С кез-келген сан болғандықтан,
қарастырылып отырған жүйе анықталмаған жүйе оның шексіз көп шешімі бар.
II - Бөлім АЛГЕБРАЛЫҚ ТЕҢДЕУЛЕР ЖҮЙЕСІН ШЕШУДІҢ ДАМЫҒАН ӘДІСТЕРІ
2. 1 Кері матрица әдісі
Алгебралық теңдеулер жүйесінің m=n болатын дербес түрін қарастырайық.
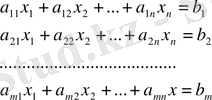 (58)
(58)
[А] х=[В] (59)

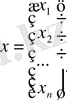
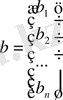 . 3
. 3
[A] матрицасы ерекше емес, яғни
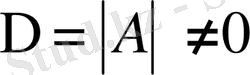 болса, Мұндай жағдайда [А] матрицасының кері [А]
-1
матрицасы бар. (59) теңдіктің екі жағын сол жақтан [А]
-1
матрицасына көбейтіп [А]
-1
[А] =Е, ЕХ=Х теңдігін ескерсек мынадай теңдікті жазуымызға болады
болса, Мұндай жағдайда [А] матрицасының кері [А]
-1
матрицасы бар. (59) теңдіктің екі жағын сол жақтан [А]
-1
матрицасына көбейтіп [А]
-1
[А] =Е, ЕХ=Х теңдігін ескерсек мынадай теңдікті жазуымызға болады
Х= [А] -1 В (60)
Мұндағы Е- n-ретті бірлік матрица (60) формуласы арқылы (58) жүйесінің шешімін табуды кері матрица әдісі деп атайды.
[А] матрицасының реті n болғандықтан кері матрица әдісімен шешімді табу қиын болуы мүмкін.
2. 2 Алгебралық теңдеулер жүйесін шешудің итерациялық әдістері
Сандық әдістер курсынан алгебралық теңдеулер жүйесін шешудің көптеген әдістері белгілі. Мысалы Крамер, Гаусс, итерация, кері матрица, Холецкий, ең кіші шаршылар (наименьшие квадраты), үшбұрышты матрицаларға жіктеу, түйіндес градиенттер, клеткаларға бөлу, қума (прогонка) т. б. әдістер бар.
ШЭӘ-де қатаңдық матрицасы
 -дің мынадай ерекше қасиеттері бар: түзілімі симметриялы, ленталық түрі бар, оң анықталған т. с. с. Осындай қасиеттерді сақтап құру үшін терең түсінік пен үлкен шеберлік керек. Осы айтылған әдістердің ішіндегі үлкен жүйелер үшін жарамдысы Гаусс пен Итерация әдістері. Тіптен үлкен жүйелер үшін бірден -бір жарамды әдіс тек итерация әдістері ғана деуге болады. Себебі өзге әдістермен бірге Гаусс әдісінің де кемшілігі қателіктер жөнделмей үнемі өсіп отырады. Ал итерация әдістерінде керісінше қателіктер жөнделіп отырады.
-дің мынадай ерекше қасиеттері бар: түзілімі симметриялы, ленталық түрі бар, оң анықталған т. с. с. Осындай қасиеттерді сақтап құру үшін терең түсінік пен үлкен шеберлік керек. Осы айтылған әдістердің ішіндегі үлкен жүйелер үшін жарамдысы Гаусс пен Итерация әдістері. Тіптен үлкен жүйелер үшін бірден -бір жарамды әдіс тек итерация әдістері ғана деуге болады. Себебі өзге әдістермен бірге Гаусс әдісінің де кемшілігі қателіктер жөнделмей үнемі өсіп отырады. Ал итерация әдістерінде керісінше қателіктер жөнделіп отырады.
Егер шешетін теңдеулер жүйесінің реті
 болса, онда итерация әдістерінде
болса, онда итерация әдістерінде
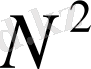 , ал Гаусс әдісінде
, ал Гаусс әдісінде
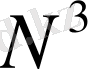 амал орындалады. Сондықтан есептеу уақыты жағынан да итерация әдісінің әлдеқайда тиімді екенін көреміз. Итерация әдістерінің өзі Якоби, Ричардсон, Зейдел, Янг т. б. түрлеріне бөлінеді. Янг әдісінің ШЭӘ - дегі бір түрі жоғары релаксация немесе Гаусс - Зейдел әдісі деп аталады. Якоби итерациясының жүйенің
амал орындалады. Сондықтан есептеу уақыты жағынан да итерация әдісінің әлдеқайда тиімді екенін көреміз. Итерация әдістерінің өзі Якоби, Ричардсон, Зейдел, Янг т. б. түрлеріне бөлінеді. Янг әдісінің ШЭӘ - дегі бір түрі жоғары релаксация немесе Гаусс - Зейдел әдісі деп аталады. Якоби итерациясының жүйенің
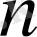 -ші қатары үшін алгоритмі мынадай
-ші қатары үшін алгоритмі мынадай
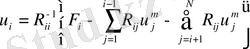 (72)
(72)
Гаусс - Зейдел алгоритмі
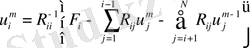 (73)
(73)
Жоғары релаксация коэффициенті
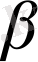 есептеу процесін қатты үдетеді.
есептеу процесін қатты үдетеді.
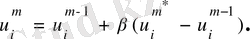 (74)
(74)
мұндағы
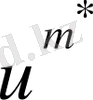 - (73) бойынша есептелген ығысу шамасы.
- (73) бойынша есептелген ығысу шамасы.
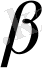 - жоғары релаксация коэффициенті. (72) - (74) - шы өрнектердегі
- жоғары релаксация коэффициенті. (72) - (74) - шы өрнектердегі
 итерация санын, немесе нөмірін көрсетеді. Көптеген есептеулер тәжірибесі мынаны көрсетті. Алгебралық теңдеулер жүйесінің шешімі
итерация санын, немесе нөмірін көрсетеді. Көптеген есептеулер тәжірибесі мынаны көрсетті. Алгебралық теңдеулер жүйесінің шешімі
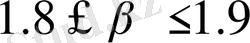 болғанда тездейді. Бұл коэффициенттің мәнін алға
болғанда тездейді. Бұл коэффициенттің мәнін алға
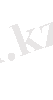 ш реет Янг былай деп ұсынған еді:
ш реет Янг былай деп ұсынған еді:
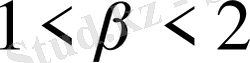 . Егер
. Егер
 болса, онда Гаусс - Зейдел әдісіне келеміз, ал егер
болса, онда Гаусс - Зейдел әдісіне келеміз, ал егер
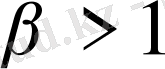 болса, онда жоғарғы релаксация әдісіне келеміз.
болса, онда жоғарғы релаксация әдісіне келеміз.
Енді осы әдісті кеңірек талдайық. Ол үшін
 матрицасын
матрицасын
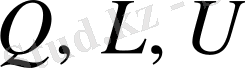 деп диагоналдық, төменгі үшбұрышты, және жоғарғы үшбұрышты элементтерін белгілейік. Бұл айтқанның Гаусс бойынша
деп диагоналдық, төменгі үшбұрышты, және жоғарғы үшбұрышты элементтерін белгілейік. Бұл айтқанның Гаусс бойынша
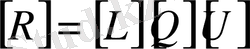 деп жіктеуге ешқандай қатысы жоқ. Шындығында
деп жіктеуге ешқандай қатысы жоқ. Шындығында
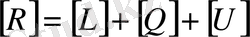 деген қосындыларға тең. Итерацияның жүруінің тездеуі мынадай өрнекпен анықталады.
деген қосындыларға тең. Итерацияның жүруінің тездеуі мынадай өрнекпен анықталады.
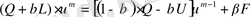 (75)
(75)
Бұл өрнектің сол жағы
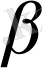 -ға қатыссыз төменгі үшбұрышты матрица да дәл солай оң жағы да
-ға қатыссыз төменгі үшбұрышты матрица да дәл солай оң жағы да
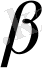 -ға қатыссыз жоғарғы үшбұрышты матрица. Бұл алгоритмның мәнісі
-ға қатыссыз жоғарғы үшбұрышты матрица. Бұл алгоритмның мәнісі
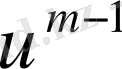 жуықтауы есептеліп бітуіне қарай
жуықтауы есептеліп бітуіне қарай
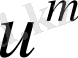 - жуықтауына ауыстырылады. Гаусс - Зейдел әдісінің бір қадамы мына өрнекпен есептеледі.
- жуықтауына ауыстырылады. Гаусс - Зейдел әдісінің бір қадамы мына өрнекпен есептеледі.
 . (76)
. (76)
Егер алдыңғы
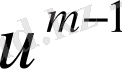 жуықтауы шын шешім
жуықтауы шын шешім
 - ға теңессе, онда жаңа жуықтау
- ға теңессе, онда жаңа жуықтау
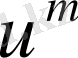 де
де
 - ға тең болады.
- ға тең болады.
Гаусс - Зейделдің итерациялық әдісі оңай программаланады. (64) - өрнекпен берілген алгебралық теңдеулер жүйесінің әрқайсысы (76) - ге эквивалентті (73) бен итерацияланады да, табылған шешім (75) - мен анықталады. Итераңия қажетті шешім табылғанша жүргізіле береді. Шешімнің табылуы қатар екі итерацияның айрымының қажетті мөлшерге (мейлінше аз шама
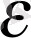 нан кіші) тең болуымен анықталады, яғни
нан кіші) тең болуымен анықталады, яғни
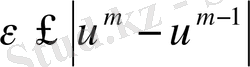 .
.
ШЭӘ-нің негізгі теңдеуі (64) - ді шешуге қолданатын әдісті таңдарда жүйенің ретіне қарау керек. Егер жазық есептерде жүйе реті p2=
 , ал кеңістіктік есептерде p3=
, ал кеңістіктік есептерде p3=
 . Бұл жердегі
. Бұл жердегі
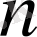 есептік облысты шекті элементтерге бөлгендегі нүктелердің саны. Егер жүйенің қатаңдық матрицасының оң анақталғандық қасиеті сақталып, p2 немесе p3 шамамен
есептік облысты шекті элементтерге бөлгендегі нүктелердің саны. Егер жүйенің қатаңдық матрицасының оң анақталғандық қасиеті сақталып, p2 немесе p3 шамамен
 100 болса, онда кері матрица әдісін қолдану керек. Кері матрица бір-ақ рет табылады да әрі қарай оң жақтарындағы күш векторы ғана өзгеріп отырады. Егер жүйенің реті 100
100 болса, онда кері матрица әдісін қолдану керек. Кері матрица бір-ақ рет табылады да әрі қарай оң жақтарындағы күш векторы ғана өзгеріп отырады. Егер жүйенің реті 100
 (p2 немесе p3)
(p2 немесе p3)
 20 000 болса онда Гаусс әдісі тиімді де, p3≥20 000 болса итерациялық әдістерді қолдану керек.
20 000 болса онда Гаусс әдісі тиімді де, p3≥20 000 болса итерациялық әдістерді қолдану керек.
2. 3 Алгебралық теңдеулер жүйесін шешудің түйіндес градиенттік әдісі
Алгебралық теңдеулер жүйесін шешудің бұл әдісін тікелей шекті элементтер әдісіне қолдану тұрғысында келтірейік. Шекті элементтер әдісінде (64) - теңдеу тепе-теңдік теңдеуі деп аталады. Физикалық мағынасы бойынша серпімді дененің деформациялану кезіндегі тепе-теңдігі сыртқы күш әсерінен онда (дененің ішкі нүктелерінде) пайда болатын серпімді деформацияланудың мүмкін түрлерінің ішіндегі потенциалдық энергиясының ең аз мөлшері байқалатын жағдайына сәйкес келеді. Сондықтан бұл жерде тепе-теңдікке жету үшін потенциялдық энергияны минимизациялау керек. Осы айтылғандарды серпімді жүйенің қатаңдық матрицасы
 , ығысу векторы
, ығысу векторы
 және сыртқы күш векторы
және сыртқы күш векторы
 арқылы шекті элементтер әдісіндегі белгілі өрнегін былай жазамыз
арқылы шекті элементтер әдісіндегі белгілі өрнегін былай жазамыз
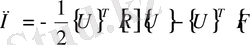 (77)
(77)
Сонымен түйіндес градиенттік әдіс дегеніміз (64) ді тікелей шешпей-ақ
 ны минимизациялайтын жинақты итерациялық процесс.
Оның алгоритмдері төмендегідей негізгі қадамдардан тұрады.
ны минимизациялайтын жинақты итерациялық процесс.
Оның алгоритмдері төмендегідей негізгі қадамдардан тұрады.
1. Қарапайым градиенттің теріс векторын, яғни (64) -ші теңдеудің сол жағындағы өрнекті оң жағына шығарғандағы айрымды кез - келген
 -ші итерация үшін мынадай алгоритмін былай жазамыз
-ші итерация үшін мынадай алгоритмін былай жазамыз
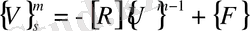 (78)
(78)
 - ды (алғашқы қадамдағы нөлінші итерация), яғни ығысу векторының элементтерін түгелдей нөл деуге болады.
- ды (алғашқы қадамдағы нөлінші итерация), яғни ығысу векторының элементтерін түгелдей нөл деуге болады.
2. Түйіндес градиент векторын есептейміз.
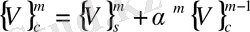 (79)
(79)
мұндағы
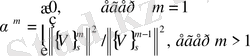
Вектордың нормасы былай есептеледі
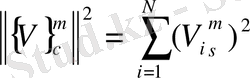
Мұндағы
 -жүйенің еркіндік дәрежесінің саны, яғни теңдеулердің саны.
-жүйенің еркіндік дәрежесінің саны, яғни теңдеулердің саны.
3. Итерация қадамының тиімді шамасын есептеу.
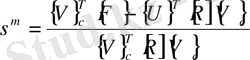 (80)
(80)
мұндағы
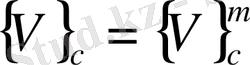 және
және
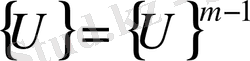
4. Итерация соңындағы ығысулардың шамалары былай тексеріледі.
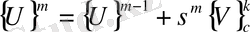 (81)
(81)
5. Жинақтылық критериін (77) де көрсетілген деформацияның потенциалдық энергия өрнегі арқылы тағайындау қолайлы. Егер жинақтылық жеткіліксіз болса 1 - 4 қадамдар қайтадан қайталанады.
Жоғарыдағы келтірілген қадамдар бірінен соң бірі орындалып отыратындықтан
1 - 5-ші қадамдарда (77), (78) - өрнектердегі
 мен
мен
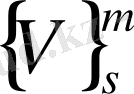 есептеу үшін матрицалық көбейтулерді қайталап орындаудың қажеті де жоқ. Оны У. Р. Маркс пен Н. Ж. Соломон байқап төмендегідей алгоритмді ұсынды. Айтылған өрнектердегі
есептеу үшін матрицалық көбейтулерді қайталап орындаудың қажеті де жоқ. Оны У. Р. Маркс пен Н. Ж. Соломон байқап төмендегідей алгоритмді ұсынды. Айтылған өрнектердегі
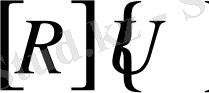 көбейтіндісін басқаша жолмен біртіндеп қосу амалын орындай отырып іске асырған әлдеқайда тиімді. Мысалы (80) - ші өрнекте қолданылатын
көбейтіндісін басқаша жолмен біртіндеп қосу амалын орындай отырып іске асырған әлдеқайда тиімді. Мысалы (80) - ші өрнекте қолданылатын
 көбейтіндісін (81) да
көбейтіндісін (81) да
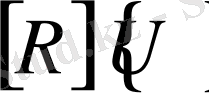 - ды есептеу үшін мынадай түрде қайтадан қолдануға болады:
- ды есептеу үшін мынадай түрде қайтадан қолдануға болады:
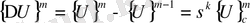 (82)
(82)
Олай болса
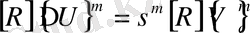 (83)
(83)
Сондықтан
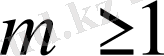 үшін
үшін
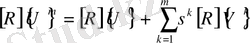 (84)
(84)
Егер
 - ды түгел нөл десек
- ды түгел нөл десек
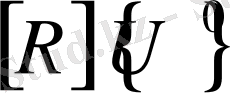 - ді де есептеудің қажеті жоқ. Бұл алгоритмды қолданғанда әр итерацияда бір ғана көбейту амалы орындалады. Көптеген зерттеушілердің пікірлеріне қарағанда (77) - (84) -шы - өрнектермен баяндалған бұл алгоритм Гаусс әдісіне қарағанда әлдеқайда тиімді. Сондықтан бұл әдіс те теңдеулер жүйесінің реті 20 000 - нан асқанда әсіресе динамика есептерін шешкенде өте қажет болады.
- ді де есептеудің қажеті жоқ. Бұл алгоритмды қолданғанда әр итерацияда бір ғана көбейту амалы орындалады. Көптеген зерттеушілердің пікірлеріне қарағанда (77) - (84) -шы - өрнектермен баяндалған бұл алгоритм Гаусс әдісіне қарағанда әлдеқайда тиімді. Сондықтан бұл әдіс те теңдеулер жүйесінің реті 20 000 - нан асқанда әсіресе динамика есептерін шешкенде өте қажет болады.
2. 4 Алгебралық теңдеулер жүйесін шешудің Холецкий әдісі
Холецкий әдісі әсіресе шекті элементтер әдісінде құрылатын алгебралық теңдеулер жүйесінің негізгі матрицасы
 қатаңдық матрицасының симметриялық әрі ленталық түріне қолдануға өте қолайлы. Бірақ алгебралық теңдеулер жүйесінің бәрі бірдей ленталық бола бермейтіндіктен бұл әдістің алгоритмдерін жалпы жағдай үшін
қатаңдық матрицасының симметриялық әрі ленталық түріне қолдануға өте қолайлы. Бірақ алгебралық теңдеулер жүйесінің бәрі бірдей ленталық бола бермейтіндіктен бұл әдістің алгоритмдерін жалпы жағдай үшін
 -ді шаршы матрица деп келтірейік. Сонда
-ді шаршы матрица деп келтірейік. Сонда
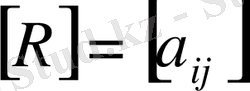
 - ші ретті шаршы матрица да
- ші ретті шаршы матрица да
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz