Процестерді математикалық модельдеу

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 38 бет
Таңдаулыға:

М а з м ұ н ы
Кіріспе 3
Қысқартылған сөздер 7
І-тарау. Процестерді математикалық модельдеу 8
1.1. Модельдеу және оның түрлері 8
1.2. Математикалық молдельдеу 10
1.3. Математикалық модельді құрудағы негізгі принциптер 11
ІІ-тарау. Қоршаған ортаны математикалық модельдеу 22
2.1. Биологиялық процестерді математикалық модельдеу 22
2.2. Биологиялық Бәске моделі 27
2.3. Биологиялық Жыртқыш - жемтік моделі 32
Қорытынды 43
Әдебиеттер 44

Кіріспе

Қазіргі таңда негізгі экологиялық мәселелерінің бірі, қоршаѓан ортаныњ
ұлттық, аймақтық және кењ ауқымды залалдарынан, барлық адам баласын қорғау
болып табылады (президент Н.Ә. Назарбаев).
Табиғаттың ластануы дегенде біз бар заттардың консентрациясының
(химиялық, физикалық, биологиялық) артуын, санның нәтижесінде қолайсыз
әсерлер туғызуын түсінеміз. Ластандырушы заттарға тек улы заттар ғана емес,
зиянды емес немесе ағзаға қажет заттың оптималды консентрациядан артық
болуы да жатады.
Ластануды жүйенің тепе – теңдігін бұзатын кез келген агент ретінде
бағалауға болады.
Ластану әр түрлі белгілері бойынша жіктеледі:
• шығу тегі бойынша:
табиғи және жасанды (антропогенді);
• пайда болу көзіне байланысты:
а) өндірістік, ауыл шаруашылық, транспорттық және т.б.;
ә) нүктелік (өнеркәсіп орнының құбыры), объектілі (өнеркәсіп
орны), шашыраған (егістік танабы, бүкіл экожүйе), трансгрессивті (басқа
аймақтар мен мемлекеттерден енетін);
• әсер ететін ауқымына байланысты: ғаламдық, аймақтық, жергілікті;
• қоршаған ортаның элеметтері бойынша: атмосфера, топырақ, гидросфера және
оның әр түрлі құрам бөліктері (әлемдік мұхит, тұщы су, жер асты сулары,
өзен сулары және т.б.);
• әсер ететін жеріне байланысты: химиялық (химиялық заттар мен
элементтер), физикалық (радиоактивті, радиациялық жылулық, шу,
электромагниттік), физико – химиялық (аэрозольдер), биологиялық
(микробиологиялық және т.б);
• әсер етудің периодтылығына байланысты: бірінші ретті (өнеркәсіп
орындарының қалдықтары), екінші ретті (смогты құбылыстардың өнімдері);
• тұрақтылық дәрежесі бойынша: өте тұрақты – 100 және 1000 жыл тұратын
(азот, оттегі, аргон және басқа инертті газдар), тұрақты – 5-25 жыл
(көмірқышқыл газы, метан, фреондар), тұрақсыз (су буы, көміртегі тотығы,
күкіртті газ, күкіртсутек, азоттың қостотығы, озон қабатындағы фреон).
Неғұрлым ластаушы зат тұрақты болса, оның қоршаған ортада жиналу эффекті
жоғары. Кез келген ластаушы затты үш параметр бойынша бағалауға болады:
қоршаған ортаға түсетін көлеміне, улылығына және тұрақтылық дәрежесіне
қарай. Мысалы, көмірқышқыл газының қолайсыз эффектісін оның қоршаған ортаға
түсетін көлеміне және ұзақ сақталу уақытына, олай болса оның жинақталуы
және осыған байланысты парниктік эффекттің пайда болуы қамтамасыз етеді.
Өндірілетін ресурстардың тек 2 – 3% ғана пайдалы өнім ретінде
қолданылады, ал қалғаны қалдықтар (бос жыныс, шлактар және т.б).
Адам қызметінің көңіл аударарлық нәтижесіне қоршаған ортаға оған тән
емес, тірі ағзалар үшін бөтен (ксенобиотиктер) заттардың шығарылуы жатады.
Табиғатта 2 мыңдай бейорганикалық және шамамен 2 млн. органикалық
қосылыстар бар. Адам қазір 8 млн. – нан астам қосылыстарды синтездей алады.
Жыл сайын олардың саны бірнеше мыңға артып отырады.
Жер бетіндегі адам мекен етпейтін кеңістіктің болуы (құрлықтың жалпы
ауданы 149 млн. км2 болса, мұндай жерлердің үлесіне шамамен 48 млн. км2
тиеді) қазіргі дағдарыстың ғаламдық сипатын жоққа шығармайды. Бұл ең
алдымен атмосфера мен судың қозғалғыштығына байланысты. Мысалы, мұнайлы
қабықшамен әлемдік мұхиттың бетінің 15 – 25% ластанған. Қазіргі кезде
атомдық двигательдер мен радиоактивтік қалдықтардың көмілуі нәтижесінде
әлемдік мұхиттың радиоактивті ластануы зор қауіп төніп отыр.
Табиғат ресурстарын пайдалану жылулық ластанумен, яғни жер маңы
кеңістігінде қосымша энергияның жиналуымен байланысты.
Биосфераның жылулық балансының бұзылуын атмосфераның шаңдануының артуы,
өсімдік жабынының булануының өзгеруі, топырақ пен су қоймаларының бетінен
ластануының өзгеруі қамтамасыз етеді. Мұнайлы қабықша булануды 20 – 30% -
ға тежейді. Нәтижеде ғалымдардың болжауы бойынша ауаның орташа жылдық
температурасы 1 – 30С – ға артады. Ал мұның өзі биосфераның
термодинамикалық немесе жылулық дағдарыс жағдайына өтуіне әкеліп соқтыруы
мүмкін.
Қазіргі кездегі озон қабатын бұзатын негізгі антропогенді фактор -
фреондар болып есептеледі. Соңғы жылдары атмосфераның жоғары қабатындағы
озонның мөлшерінің кемуі байқалуда. Солтүстік жарты шардың орталық және
жоғары ендіктерінде бұл кему 3% құраған. Мәліметтер бойынша озонның 1% - ға
кемуі терінің қатерлі ісігімен ауру деңгейін 5 – 7% - ға арттыруы мүмкін.
Көптеген мемлекеттер фреондардың өндірісін 50% кеміту және оларды басқа
пропиленттермен алмастыру туралы міндеттеме қабылдады.
Ластануға судың барлық категориялары: мұхит, континенттік, жерасты,
әртүрлі дәрежеде ұшырайды.
Судың ластануы ең бірінші рет су қоймаларына әр түрлі ластаушы заттардың
келіп түсуіне байланысты болады. Екінші ретті ластану бірінші ретті
ластаушылардың әр түрлі тізбекті реакцияларға түсуі арқылы жүреді.
Ластаушы заттарға негізінен топырақ эрозиясының өнімдері, минералдық
тыңайтқыштар, улы химикаттар және т.б заттар жатады. Ластаушы заттардың
басым көпшілігін амосфералық жауын – шашын әкеледі. Сулардың канализация
ағысымен, тұрмыстық қалдықтармен, өнеркәсіп орындарының қалдықтарымен, су
таранспорттарымен ластану үлесі де жоғары. Қазір бүкіл планетада іс жүзінде
қандай да бір дәрежеде адам қызметі нәтижесінде ластанбаған беттік тұщы су
көзі жоқ деуге болады.
Қазіргі кезеңнің өзекті мәселелерінің бірі – радиациялық ластану болып
қалып отыр. Қазақстан территориясында қуатты ядролық сынақтардың ең көп
мөлшері жасалды. Олар еліміздің территориясының біраз бөлігінің
радиациялық ластануына әкелді. Қазақстан территориясында радиациялық
ластану себептеріне мыналар жатады: Семей ядролық полигонында жасалған
жарылыстардың салдары, радиоактивті материалдарды пайдаланатын атомдық
өнеркәсіп орындары, жауындар, халық шаруашылық мәселелерін шешу мақсатында
жасалған жер асты ядролық жарылыстар, табиғи радиоактивтілік, радиоактивті
қалдықтар.
Дипломдық жұмыста түрлі экологиялық процестерді математикалық
модельдеу мәселелері қарастырылды. Компьютерде процестерге талдау жасалып,
қорытындалды.
Диплом жұмысы екі тараудан, қорытындыдан және әдебиеттер тізімінен
тұрады. Бірінші тарауда интернет жайлы модельдеу және оның түрлері,
математикалық молдельдеу және математикалық модельді құрудағы негізгі
принциптер қарастырылған. Екінші тарауда қазіргі уақытта биологиялық
процестерді математикалық модельдеу, биологиялық Бәске және
Биологиялық Жыртқыш - жемтік моделдері мен мәселелері қарастырылған.
Диплом жұмысы 4 суретпен, 4 кестемен көркемделген.

Қысқартылған сөздер

БҚ – Бағдарламалармен қамтамасыздандыру
АЖ – Ақпараттық жүйелер
ДҚ – Деректер қоры
МБ – Мәліметтер базасы
МҚБЖ – Мәліметтер қорын басқару жүйесі
ОЖ – Операциялық жүйе

МҚ – Мәліметтер қоры

ДК – Дербес компьютер
ЭЕМ – электронды есептеуіш машина
ЕТ –есептеуіш техника
ММ – Математикалық модельдеу

І-ТАРАУ. ПРОЦЕСТЕРДІ МАТЕМАТИКАЛЫҚ МОДЕЛЬДЕУ

1. Модельдеу және оның түрлері

Қоршаған ортамен араласып, қарым-қатынас жасаудың нәтижесінде адам өз
танымына қарай модель құрайды. Танымдық процесс зерттелінетін объектіге
және зерттеуші субъектіге байланысты. Зерттелінетін объектіде болып жатқан
оқиғаны бақылап, керек болса оқиғаға кірісіп, қойған сұрақтарына жауап
алумен қатар, объектіге қатысты информацияларды жинақтап, қорытып, субъект
пен объектіге тән құбылысты түсініп, өзінің көзқарасын белгілі бір формада
бекітеді. Осы затқа тән нақтылы информацияларға негізделген зерттеушінің
субъективтік танымы-объектініең моделі болып есептелінеді.
Танымдық процестің негізгі қызметі-информацияны жинау, сақтау және
қорыту болса, осылар модельдеудің негізгі сипаттамасын береді деуге болады.

Қоршаған дүниені ұғудың танымдық типтері, әрі нақты процесті
сипаттаудың жолы әртүрлі. Ал бұларға ортқ тән қасиет бар. Мысалы, ғалым
атом құрылысын, қоғамның өмір сүру заңдарын; философ - өмір туралы және
адамның өмірлігі орны; дін-адамның мәңгілік жасау мүмкідігін, құдайдың
қағидалық ұғымдары туралы; жазушы детективтік роман немесе трагедиялық
әңгіме жазады; суретші теңіз жағасындағы күннің бату кезіндегі құбылысты
беретін немесе басқа суреттер салса, ал композитор бір оқиғаға арнап
симфония жауы мүмкін.
Осы зерттеушілердің қайсысы болмасын өзін қоршаған ортаны түсіну
үшін, әртүрлі құралдың көмегімен өзінің танымын жинақтайды. Сөйтіп
зерттеушілер процесті еріксіз модельдеу арқылы өзінің көзқарасын береді.
Модельдеудің түрлері көп. Модельдеуді жалпы үлкен екі топқа бөледі:
материалдық (заттық) және идеальдық. Материальдық дегеніміз – зерттелінетін
объекттің геометриялық, физикалық, динамикалық және функциональдық
сипаттамасына негізделеді.
Физикалық модельдеуге – ұқсастық теория негізінде нақты объектінің
кішірейтілген немесе үлкейтілген көшірсмесін қолданып, лаборатоиялық
жағдайда процесті қайталап, тәжірибе жасап ұғу жатады. Мысалы, гидротехника
- өзенді немесе су қоймаларын модельдеу, ал аэродинамикада- ұшатын
апараттың кішірейтілген модельдері арқылы зерттеу, архитектурада-үйдің
макетін қолдану т.б.
Аналогтық модельдеуге – зерттелінетін объектілердің физикалық
табиғаты әртүрлі құбылыстарда жүретін процестердің арасындағы байланысты
білдіретін ұқсастық теорияны қолданып, зерттеу жатады. Мұндай процестер
бірдей материальдық теңдеумен, немесе логикалық сызбалармен беріледі.
Қарапайым мысал ретінде механикалық тербелістерді электрлік сүлбе бойынша
зерттеуге болады. Мұндағы процестер аналогиялық құбылыстарға жатады.
Сондықтан екеуі бірдей теңдеумен сипатталады.
Бұл екі типтес модельдер берілген объектілердің заттық баламасына
негізделген, өзара геометриялық, физикалық және басқа сипаттамалармен
байланыста қарастырылады. Сондықтан материальдық модельдеу өзінің табиғаты
жағынан эксперименттік тәсілге жатады.
Заттық модельдеуден идеалдық модельдеу принципі мүлде басқа. Заттық
зерттеу объекті мен модельдеудің материалдық аналогиясына негізделсе,
идеалдық зерттеу танымдық процестің негізінде құрылған ойдың, идеалдық
аналогиясының жемісі болып табылады.
Сөйтіп, идеальдық модельдеу теориялық сипаттамадан тұрады да,
интуитивтік және таңбалық болып екіге бөлінеді. Интуитивтік модельдеу
дегеніміз – зерттелінетін объекті мен зерттеушінің сезім мүшлеріне әсер
етуіне байланысты топшыланған информациялардың жиынтығы. Мысалы, адамның
өмірде жинаған тәжірибесі қоршаған дүниенің интуитивтік моделі болады.
Таңбалық модель – зерттелінетін объектіге қатысты информацияны белгілі бір
тәртіпке сүйеніп, таңбаларға түрлендіріп мысалы, сүлбеге, графикке,
сызбаға, формулаға, т.б. таңбаларға жинақтау. Таңбалық модель құрылымның
түзейтін элементтер заңдылыққа, алгоритмге бағынып, өзіне тән элементтер
заңдылыққа, алгоритм бағынып, өзіне тән ережелер жүйесінде жұмыс істейді.

1.2. Математикалық молдельдеу

Математикалық модель – таңбалық танымның негізіне жатады. Классикалық
мысал ретінде механиканың заңдарын Ньютонның математикалық формулаларын
қолданып зерттеуге болады.
Бізді қоршаған дүниедегі объектілердің ғылыми танымдылығымен жеткізу үшін
әртүрлі математикалық тәсілдер қолданылады.
Физика мен химияның, биология мен психологияның, социология мен
архелогияның қолданылуы толық айқындалып, әрі қарай дамуда. Лазерлік
шашырау және ацетиленді синтездеу, клеткалардың құрылысы және жеке
меншіктің өмір сүру принциптері, жер қабатының эрозиясы және Рим
империясының құлдырауы нақтылы объектілерге байланысты жүрді. Бұларды ұғу,
зерттеу адамзат үшін міндетті болды. Себебі бұның бәрі бізді қоршаған
өмірде болған оқиғалар. Ал математика болса тек қана абстрактылы
ұғымдардан, яғни сандардан, функциялардан, жиындардан, қисындардан тұрады.
Бұның бәрі, негізінде, табиғата жоқ, адам миының ойлау қабілетінің
нәтижесі. Сөйтіп, математика операциялық жұмысты идеалдық дүниемен адам
идеасы бойынша атқарады.
Өмірде кездесетін ғылымдардың көбі бір-бірімен байланысты болғанымен,
қолдану шекарасы айқындалған. Физикамен айналысатын таза физик жекеменшік
формаларының өзара қатынасын түсіндіре алмайды. Тарихшыға химиялық
реакцияны зерттеу қиын. Дәрігер ядролық ұсақ бөлшектердің өзара әсерлесу
заңдылығын медицина ғылымында қолданып, түсіндіре алмайды. Ал, өзінің
қадірін білетін математиктің алдында ешқандай кедергі тұрмайды. Әр түрлі
ғылыми пәндердің жасанды шекарасы математика моделін қолдануға бөгет
болмайды. Таза математик бола тұрып, адамзаттың әртүрлі формадағы қызметіне
батыл кірісіп, айтарлықтай жетістіктерге жетеді. Осыдан математика өзіне
тән қасиеттер арқылы, барлық саланы қамтуға тырысатындығы және нақты не
бере алады деген ой туады. Физика, социология немесе географияға қолданған
ғылым – деген термин математикада өзін ақтай алады. Нақты қойылған
есептерді шығарудағы абстрактілі математикалық методтардың түсіндіруге
болады.
Қоршаған ортада кездеспейтін сандар, функциялар, теңдеулер,
операторлар планеталардың қозғалысын, химиялық элементтердің өзара
әсерлесуін, генетикалық информацияның берілуін, еркін нарықта бағаның
алмасу механизмін т.б. процестердің сырын түсіндіріп, анықтайды.
Математика мен бізді қоршаған нақты өмірді байланыстырушы арнайы
звеноның түрі - модель болады. Модель бір жағынан зерттелінетін объектіге
тиісті бай информацияны қамтыса, екінші жағынан математикалық стандартты
формула таңбаларынан тұрады. Яғни математикалық аппаратты қолдануға
мүмкіндік береді.

3. Математикалық модельді құрудағы негізгі принциптер

Қазіргі ғылыми тұрғыдан қарағанда бірінші математикалық модель құру
Галилейдің атымен байланысты. Аристотельдің дененің құлауына байланысты
тұжырымы (гравитациялық және инерттік масса туралы) дұрыс емес екенін
дәлелдеу үшін Галилей салмағы әртүрлі екі денені алып, атақты пизандық
башнядан бірдей биіктіктен жіберіп, эксперимент жасап, әртүрлі екі дене
бірдей үдеумен құлайтындығын дәлелдеген. Енді дене биіктіктен құлаған
уақыттағы процесті математиканың көмегімен зерттейік. Дене жерге еркін
құлағанда, процесті анықтайтын негізгі шама- биіктік уақытқа байланысты
өзгереді. Зерттелінетін процесті, кез-келген уақытта өзгеретін биіктікті
y=y(t) сипаттайтын функциямен беруге болады. Енді біздің мақсатымыз, кез-
келген уақыт моментіндегі биіктікті анықтайтын функционалдық байланысты
тапсақ, онда алынған модельдің көмегімен дененің құлау процесін уақытқа
байланысты зерттеуге болатындығына көз жеткіземіз.
Дененің қозғалысы құлау биіктігіне байланысты өзгереді. Қарастырылып
отырған шама қаншалықты тез өзгереді деген табиғы сұрақ туындайды.
Белгісіз y(t) функцияны табу үшін жылдамдығын бағалау қажет. Ал,
математикалық тұрғыдан y(t) - функцияның t – нүктесіндегі жылдамдығы
осы функцияның туындысымен 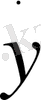анықталады. Бұны дененің құлау
жылдамдығы v деп белгілейік.
Егерде дененің жылдамдығы v(t) белгілі болса, y(t) – функциясын
табу үшін мынадай қатынас аламыз:

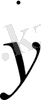= v (1.3.1)

Алынған есеп (1.3.1) дифференциалдық теңдеу түрінде беріліп тұрған,
зерттелінетін процесстің жуық математикалық моделі болады. Белгісіз
функцияның уақытқа байланысты бірінші ретті туындысы кіріп тұрғандықтан,
бірінші ретті жай дифференциалдық теңдеу дейміз.
Екінші этапта алған қарапайы модельден, математикалық тәсілдің
көмегімегімен информация алуға болады. Функционалды байланысты табу үшін
(1.3.1) теңдеуді шешу қажет, яғни модельдегі бар информацияларды
түрлендіру. Егерде дененің жылдамдығы уақытқа тәуелді өзгермейді деп
қарастырсақ, онда (1.3.1) теңдеуді кез-келген тұрақты шамамен (с)
дәлдігімен жалпы шешімін, былай жазамыз:
y(t) = v t + c (1.3.2)

Үшінші этапта осы модельдің көмегімен зертелінетін құбылыстан алатын
ақпаратымызды талдауға болады. Модельден алынған нәтижені, жасалған
экспериментпен салыстырып, толық анализ жасасақ, онда біз құрған
моделіміздің табиғи процесстен қаншалықты алшақтығын байқаймыз.
Модельдің шешімі тұрақты шамаға с байланысты. Ол үшін бірінші этапты
қайта қарастырып, моделімізді жетілдіреміз.
Модельді жетілдіру табиғи процесспен байланысты болғандықтан, кез-
келген этапта жүреді. Біздің жағдайда, белгілі жылдамдықпен құлаған дене
бастапқы момент уақытында t = t0 қандай биіктікте y0 , тұрғаны
белгілі болуы керек:
y(t0) = y0 , (1.3.3)

Сонымен, бастапқы шартқа байланысты қойылған (1.3.1), (1.3.3) Коши есебін
алдық.
Бастапқы шартқа сәйкес шешімін алу үшін (1.3.2) формулада t = t0
деп алып, нәтижесін былай жазамыз:
y(t0) = v t0 + c = y0,

Осыдан тұрақты шаманы табамыз c = y0 - v t0 .
Сөйтіп, (1.3.1), (1.3.3) Коши есебінің нақты шешімін мынадай түрде аламыз:

y(t) = y0 + v (t - t0 ) (1.3.4)

Медельден алған ақпаратымызды тағы да табиғи процесспен салыстырсақ,
нәтижелерінің бір-бірінен алшақ жатқанын байқаймыз. Себебі, эксперименттің
нәтижесі бойынша, құлаған дененің жылдамдығы уақытқа байланысты өзгеріп
отырады. Модельді жетілдіру үшін енді Коши есебіне айнымалы жылдамдықты
ескеріп қарастырамыз.
Бірінші этаптағы (1.3.1) теңдеуді, (1.3.3) бастапқы шартын ескеріп,
t0 уақыттан t -ға дейін интегралдап, құлаған дененің уақытқа байланысты
өзгеру заңдылығын табамыз:
y(t) = y0 + 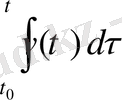(1.3.5)
Егер жылдамдық тұрақты болса (1.3.5), формула белгілі (1.3.4) шешімін
береді. Енді бізге табылған функционалды тәуелділікті бақылау нәтижесімен
салыстыру қажет. Бірақ, өкінішке орай, дене жылдамдығының өзгеру заңы бізге
белгісіз боғандықтан, мұндай мүмкіншілік бізде жоқ.
Сонымен зертеліп жатқан процесс тек координатамен ғана емес, құлап
келе жатқан дене жылдамдығымен де сипатталады. Біз математикалық модельге
кейбір қосымша мәлімет керектігіне көз жеткіземіз.
Құлап келе жатқан дене жылдамдығы қалай өзгеретіндігін бақылайық.
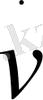функциясының туындысын механикада үдеу деп аталып, а – мен
белгіленеді. Соңында, жылдамдықты табу үшін біз тағы бір дифференциалдық
теңдеу аламыз:
(1.3.6)
Математикалық тұрғыдан алғанда (1.3.1) теңдеуге сәйкес тағы да
бастапқы шарттар қажет етеді. Мысалы, t = t0 уақыт моментінде дене
қозғалысты жаңа ғана бастады десек, яғни жылдамдығы нольге тең деп
есептейміз. Бұған мына теңдік сәйкес келеді:
v(t0) = 0 (1.3.7)
Модельдеудің келесі сатысында бастапқы шарттарды (1.3.3) және (1.3.7)
дифференциалды теңдеу (1.3.1), (1.3.6) жүйесі пайда болады. Коши есебі
(1.3.6), (1.3.7) y функциясымен бірдей а үдеу тұрақты ма, айнымалы ма
соған байланысты (1.3.4) немесе (1.3.5) формулалар арқылы жалпы
шешімінің бар болуы орындалады. Қандай жағдайда болмасын, құлап келе жатқан
дененің жылдамдығының заңдылығын оның туындысын, яғни жылдамдықты табуымыз
керек. Егер біз үдеу туындысын, оның туындысының туындысын табатын болсақ,
тіпті ыңғайсыз жағдайға тап болар едік. Алайда, дәлелденген тәжірибеге
сүйенсек, құлап келе жатқан дене үдеуі уақытқа сәйкес өзгермейтінін, тіпті
қарастырып отырған дене ерекшіліктеріне тәуелсіз, әмбебап физикалық тұрақты
шама екен. Бұл керемет факт бізге өткізіп жатқан зерттеуді бітіріп, көптен
күткен шешімді табуға көмектеседі.
Қозғалыс кезінде, құлап келе жатқан дене биіктігі азаяды. Бұл (1.3.1)
теңдеуге байланысты v жылдамдықтың теріс мәнінде орындалады. Уақыт
моментінің басында нольге тең және а-ның жылдамдығына байланысты өзгеретін
қандай да болмасын v функциясы тек а=0 теңсіздігі орындалса ғана теріс
бола алады. Оң шама g еркін түсу үдеуі деп аталады және процесстің өту
шартына тәуелсіз абсалютті тұрақты болып табылады. Осылайша (1.3.6)
сйкестікті төмендегінше жазуға болады:.
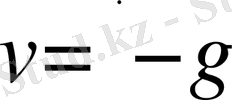(1.3.8)

Бастапқы шарттары (1.3.3), (1.3.7) бойынша берілген дифференциалды
теңдеулер (1.3.1), (1.3.8) еркін түсу үдеуінің математикалық моделін
құрайды. Егерде бастапқы құлау уақыты t0 = 0 деп алсақ. Онда (1.3.8)
теңдеуді (1.3.7) бастапқы шарты бойынша шешіп, құлайтын дененің
жылдамдығы мынадай заңдылыққа бағынатынын табамыз v(t) = - g0 t . Осы
табылған мәнін және t0 = 0 шартын ескеріп (1.3.5) формулаға
қойып, құлаған дененің биіктігінің уақытқа байланысты өзгерісін табамыз:

y(t) = y0 - g t2 2 .

y0 - бастапқы биіктік.

Құлаған дененің биіктігінің уақытқа байланысты өзгеру заңдылығын
беретін математикалық формулалардың нәтижесін эксперименттің нәтижесімен
салыстырып, модельдің дұрыс қойылғанына көзіміз жетеді. Енді математикалық
модельдің қасиетіне сүйене отырып, зерттейтін құбылыс туралы қосымша
мағлұмат алуға болады. Уақыттың t = T мәнінде дененің биітігі y(T) =
0 болады. Ендеше соңғы теңдіктен бастапқы биіктігіне байланысты жерге
құлаған уақытын табамыз:

T =

Дененің құлағандағы t = T момент уақытына сәйкес, соңғы жылдамдығын,
яғни процессті тағы бір сипаттаймыз:

v(T) = -

Осылай талдау принципі кез-келген құбылысқа тән болғандықтан,
математикалық модельдеудің негізгі этаптарын былай беруге болады (Кесте
1).

Математикалық модельдеудің негізгі этаптары
Кесте 1.

№ Этап Мақсат Құрал
1 Модель құру Процесстің математикалық Ғылымда анықталған табиғат
сипаттамасы заңдары
2 Модельге анализ Модель формасына тән жасырынМодельдің математикалық және
ақпаратты табу компьютерлік анализі
3 Модельді Модельдің адекваттылығын Модельдік анализді
идентификациялау тексеру экспериментпен салыстыру
4 Модельдің Процесс туралы информацияны Болжам жасау, басқару т.б.
қолданылуы жетілдіру үшін модельдің есептер шығару.
қасиетін қолдану

Алынған математикалық модель туралы қорытынды жасайық. Теңдеу (1.3.1) және
(1.3.2), 0 t T уақыт интервалына сәйкес келетін құлау процессін
сипаттап, дененің биіктігі нольге тең болғанша орындалады:

y(T) = 0

Әрине y0 параметр, оң болу керек, яғни дене жердің бетінде жатқан жоқ:

y0 0 .

Ал процесс t = T болса, (1.3.9) шарт бойынша тоқтайды.

Сөйтіп, 0 t T уақыт интервалында зерттелінетін процесстің
толық математикалық моделі күйді сипаттайтын теңдеу (1.3.1), (1.3.8)
бастапқы шарттары (1.3.3), (1.3.7) бойынша беріледі. Бұған жүйедегі
y0 парамерді анықтау үшін және құлауға кеткен соңғы уақыттың шамасын
табу мақсаты қосымша қойылады.

Біздің моделіміз табиғи процессстің кейбір дара жағын қамтиды.
Сондықтан, зертелінетін құбылыс жайлы информацияны толық алу үшін,
процесстің математикалық моделін жетілдіру қажет. Мысалы, біз процессті
модельдеу кезінде, ауаның кедергі күшін ескермедік және басқа да сырттай
әсер ететін күштер болуы мүмкін. Оның үстіне дененің массасы, өлшемі,
формасы және бұл шамалардың уақытқа байланысты өзгерісі ескерілмейді.
Осыған қарамастан алған моделіміз үшін табиғи процессті сипаттайтын
механиканың заңдары орындалады. Қандай да болмасын құрылған математикалық
модель зерттелінетін құбылыс жайында толық ақиқат информация береді деп
айтуға болмайды. Ал, ақиқат информацияға жету үшін математикалық моделдің
жетілдіріле беруі табиғи процесс.

Математикалық модель құруға байланысты кездесетін негізгі
заңдылықтарды түсіндіру үшін, еркін құлаған дененің моделіне тоқталайық. Ең
алдымен, зерттелін құбылыстың негізі болатын объектіні анықтау. Біздің
жағдайда құлайтын денеге сипаттама беру. Яғни дененің формасын, өлшемін
және ішкі структурасын ескермей, біз материалдық нүкте деп қарастырдық.
Келесі, қарастырылатын процессті сипаттайтын жүйедегі күйді
анықтайтын функцияны табу. Біздің жағдайда құлаған дененің жер бетінен
қандай биіктікке болғаны және жылдамдығын анықтау. Мысалы, жылу физикасында
температура – күй функциясы боады, ал кинетикалық хмимяда өзара әсерлесетін
заттардың және өнімі болатын заттардың концентрациясы т.с.с. Сонымен
математикалық модель дегеніміз – күйді сипаттайтын функциялар бойынша
берілген теңдеу.
Енді теңдеуді шеше отырып, біз математикалық модельді зерттейміз,
яғни күйдің функцияларының басқа параметрлермен байланысын тауып,
сипаттамасын анықтаймыз. Әуелі бұған жататындар тәуелсіз айнымалы шамалар –
уақыт және кеңістік айнымалылары. Мысалы, құлаған дененің кез-келген уақыт
моментіндегі биіктігі. Ал жылу тасымалдау процессінде дененің нүктелерінде
температураның өзгерісі т.с.с.
Құрылған математикалық модельге байланысты, күйдің функцияларын және
тәуелсіз айнымалыларды анықтағаннан кейін координаталық жүйесін анықтау
қажет.
Осыдан бастап жүйеде қарастырылатын күй функцияларының өзгеру
заңдылығын беретін математикалық формуланы анықтау болады. Бұл үшін
уақиғаның дауын нақты әсер еткен не, яғнии системаның эвалюциясының себебін
көрсету қажет. Мысалы, қарастырған есепте дененің құлауына негізгі себеп
болған, денегі әсер ететін – ауырлы күш.
Бізді қызықтыратын уақиғаны туғызған себептерді көрсету үшін,
модельдеу процессін құру кезінде салдар туғызатын себептердің әрқайсысының
қандай әсер болатынын білу қажет. Сөйтіп, математикалық модельдеу негізі
дегеніміз – осы салдарлық – себептердің әсеріне байланысты күй
функцияларының өзгеру заңдылығын анықтау. Біздің мысалға келсек, мұндай
байланыс Ньютонның екінші заңымен беріледі, яғни күй функциясының уақыт
бойынша алынған екінші туындысы, әсер ететін ауырлық күшке пропорционал
өзегереді.
Зерттелінетін құбылыстың салдарлық – себептер байланысын анықтайтын
математикалық моделін толықтыратын басқа сипаттамасына тоқталайық. Бұл
зертелінетін табиғат құбылысының бізге керекті шарттарын анықтайтын жүйе
параметрлерін анықтау. Дененің еркін құлауына байланысты, бастапқы биіктік
және бастапқы жылдамдық болады. Ал, жылу тасымалдау процесіне дененің жылу
қасиеттерін беретін физикалық шамалар жатады.
Келесі жүйе параметрлерінің өзгеру диапазонын белгілу болады. Бұл
дегеніміз, математикалық модельдің қолданылу мүмкіндігін анықтайтын
шарттары туралы мәліметтер белгілі болу керек. Мысалы, дененің еркін
құлауын сипаттайтын модель тек гравитациялық өрісте қолданылатын
зерттеушілерге мәлім.
Сөйтіп, математикалық модельдің құрамы жөнінде үш сипаттамаға назар
аударуға болады. Әрбір нақтылы жағдайды сипаттайтын процесстің
параметрлері, белгіленген шамалардан тұрады және осылардың ақпаратарынан
құралады. Мұнда тәуелсіз айнымалылар белгіленбеген, бірақ өзгеру обласы
болады. Параметрлері берілген айнымалылар бойынша, күй функциясын қалпына
келтіру есебі математикалық модельдің негізгі жұмысына жатады.
Керекті математикалық ара – қатыстарды қорытып алған соң, күй
функциясынан басқа шығатын инфорацияларды анықтау қажет. Мысалы, дененің
жерге құлғандағы уақыт моментін және соңғы жылдамдықты шығатын информацияға
жатқызуға болады.
Зерттелінетін математикалық моделін құрайтын элементтерге мыналар
жатады:
1. Зерттелінетін объект.
2. Жүйе күйінің функциясы.
3. Тәуелсіз айнымалылар.
4. Координат жүйесі.
5. Жүйе эволюциясының себептері.
6. Салдарлық – себептер байланысы.
7. Жүйенің енетін параметрлері.
8. Математикалық модельдің қолданылу шарттары.
9. Жүйенің шығатын параметрлері.

Дененің құлау процесіне байланысты құрылған математикалық модельдің
негізгі элементтерінің сипаттамасы көрсетілген (Кесте 2).
Дененің құлау процесі математикалық моделінің негізгі элементтері.
Кесте 2
№ Элементтер Дененің құлау процесі
1 Зертелінетін объект Құлайтын дене
2 Күй функциясы Дененің биіктігі (координатасы), оның
жылдамдығы
3 Тәуелсіз айнымалы Уақыт
4 Координат жүйесі Координат басы-жердің беті
5 Эволюция себептері Ауырлық күш
6 Салдарлық-себептер Координат бойынша екінші туындысы ауырлық
байланысы күшке пропорционал
7 Енгізілетін параметрлер Дененің бастапқы биіктігі
8 Модельдің қолдану шарттары Жерге құлаған моментке дейін дененің
қозғалысы
9 Шығатын шарттар Құлау уақыты, құлаған уақыттағы дененің
жылдамдығы

Табиғи құбылыстағы заңдылықты анықтау үшін өзіне тән салалар
зерттейді (физика, химия, биология, және т.с.с.). Ал математикалық
амалдарды қолданып, модельді құрып, компьютердің көмегімен анализ жасап,
әрі табиғи процессті қалағанымызша қайталап, дисплейде тәжірибе жасап, көз
жеткізіп, кез – келген құбылысты зерттеуге мүмкіндігі зор.

Математикалық модельді классификациялау

Математикалық модельдің сипаттамасы модель құру үшін қолданылатын
математикалық қисаптар мен оларға кіретін шамалардың арасындағы ьайланыспен
анықталады. Күй функциясы уақытқа тәуелді өзгерсе, онда жинақталған
параметрлік жүйеде, ал күй функциясы уақытқа және кеңістік айнымалыларына
байланысты өзгерсе – тарамдалған параметрлік жүйеде берілді деуге болады.
Бұған маятниктердің тербелісін, снарядтың ұшуын кейбір дербес жағдайдың
жинақтарын қарастыруға болады, жылудың тасымалдануы, көлем ішіндегі
сұйықтықтың қозғалысы- тарамдалған параметрлік жүйеде зерттелінеді.
Математикалық қисаптарда жай дифференциальдық теңдеу жинақталған
параметрлік жүйеде кездессе, ал дербес туындылары бар дифференциальдық
теңдеу тарамдалған параметрлік жүйеде қарастырылады.
Теңдеулерді қолданып қоймай, кейбір процесстерді модельдеу үшін
вариациялық принциптер негізінде әдістелмейді. Классикалық механикадан
материалдық нүктенің қозғалысын динамиканың теңдеуін қолданып немесе ең аз
әсер ету принципінің негізінде, яғни жүйе эволюциясын құрғанда шығатын
энергияның шамасы минимум болатындай есеп құрып шығаруға болады.
Процеске кездейсоқ факторлар әсер етсе, стохастикалық модель деп, ал
сырттай әсер ететін факторлардың эффектілігін ескермей құрылған модель
детерминальдық делінеді. Үздіксіз жүйеде тәуелсіз айнымалы үздіксіз
өзгереді, ал дискретті жүйеде тәуелсіз айнымалы тұрақты немесе айнымалы
қадам жасап өззгереді. Күйді сипаттайтын функциялар уақытқа байланысты
өзгерсе динамикалық, ал күйдің сипаттамаларын беретін шамалар уақыт
өзгерісіне қатысы жоқ болса, стационарлық жүйе деп айтылады. Математикалық
модельдердің зерттелінетін процесті беру ерекшіліктеріне қарап,
классификациялаудың басқа да түрлерін атауға болады.
Біз биологияның көп салаларының бірі, популяциялану динамикасын
қарастырайық. Шектелген территориядағы биологиялық бірнеше тіршіліктердің
қатар өмір сүру күресіне байланысты болатын драмалық оқиғамен таныстырамыз.
Жеке–дара тіршіліктің эволюциясынан бастайық. Егерде бұл қарастырылатын
тіршіліктің туы өрбуі өлім-жітіміне қарағанда басым болса, өкінішке орай,
құрып кетеді. Тіршіліктің қорегі шектелгеніне қарамастан табиғи өсімі оң
болса, жүйенің тұрақты жағдайы орындалады, бұл дегеніміз тіршіліктің туып-
өсіп тұрақтануына қажетті қорегі бар деген сөз.
Бірнеше биологиялық тіршілік қатар өмір сүрсе, қызықты да әртүрлі
процестің куәсі боламыз. Екі тіршіліктің қатар өмір сүруі әртүрлі формада
болуы мүмкін. Қарастырылатын модельдердің біреуінде қорегі ортақ болғанда,
тіршіліктер өмір сүру үшін өзара бәсеке күресін бастайды, мұндай жағдайда
күресуге шамасы нашар тіршіліктің эволюциясын сипаттайтын теңдеу-әртүрлі
процестер болса да, мысалы, екімодолық лазер немесе химиялық бәсеке
теңдеулерімен бірдей болатынын көрсетеміз.
Екінші зерттелінетін модель бойынша бір тіршілік екінші тіршілікпен
қоректенеді. Мұндай биологиялық процеске мысал ретінде Вольтера –Лотканің
теңдеуімен берілетін атақты “жыртқыш-жемтік” модельін келтіреміз. Осы
теңдеулермен кейбір химиялық реакция процестері берілетінін көрсеткеміз.
Модельдік теңдеулер жүйесін өлшемсіз параметрлер арқылы жазып, биологиялық
процеске сапалық анализ жасаймыз. Келесі модель, әр тіршілікке өзіне тән
қорегі қажет болған жағдайда биологиялық процесс “экологиялық қуыс”,
моделімен беріледі. Қажетті қоректері болса, мұндай екі тіршілік иесі тірі
қалып, өмір сүру тұрақтылығы сақталуы мүмкін. Енді, екі биологиялық
тіршіліктің өмір сүруі бір-біріне ыңғайлы әсер етсе және бір – бірінсіз
өмір алмайтын жағдайда болса, онда “симбиоз”математикалық моделімен беруге
болатынын көрсетеміз. Симбиоз жағдайында екі тіршіліктің бірдей өмір сүріп
шектелмей көбейуі байқалатынын немесе бірдей құрып кету жағдайында болу
мүмкіндігін көрсетеміз. Мұндай процесстерде қорек шектелген болса, екі
тіршіліктің эволюциясы тұрақты түрде дамиды.

ІІ-тарау. Қоршаған ортаны математикалық модельдеу

2.1 Биологиялық процестерді математикалық модельдеу

Кез келген құбылысты зерттеп үйренуде, бастапқы кезде мәселенің сапалы
сипатын аламыз. Модельдеу кезеңінде сапалы сипат санды сипатқа өтеді.
Бұл кезеңде жүйенің әр бір кіріс-шығыс берілгендердің әр бір нұсқасы
үшін айнымалылар арасындағы байланыс функционалды тәуелді болады.
Модельдерді құру – формальды болмаған процедура болып, зерттеушінің
тәжірибесіне өте байланысты және анық тәжірибе материалына жандасады.
Құрылған модель құбылысты дұрыс сипаттауы және қолдануға өте ыңғайлы
болуы қажет. Сондықтан модельді детализациялау дәрежесі және оның формасы
зерттеуге байланысты.
Тәжірибе материалын үйрену мен формалдау, математикалық модельді
құрудағы жалғыз әдіс емес. Дербес құбылыстар молдельдерін, құбылыстарды
жалпы сипаттаушы модельдерден алу, ең маңызды рөл ойнайды.
Бүгінгі күнде математикалық модельдеу әдісі білімнің түрлі салаларында
қолданылады. Жалпы сипатқа ие болған, бірнеше принциптер мен жандасулар
жасалды.
Ғылыми талдаудың негізгі есебі, ойша қабылданған қозғалыстар жиынынан,
нақты қозғалысты ерекшелеу және еркшелеу принциптерін сипаттау болып
табылады. Мұндағы “қозғалыс” термині кең мағынада қолданып, кез келген
материалды объектілердің өз ара әсерлерін түсінеміз.
Білімдердің түрлі салаларында қозғалыстарды таңдау принциптері
түрлішіе.
Материяны ұйымдастыруда үш деңгей айырмашылығы қабылданған:
• Тірі болмаған;
• Тірі;
• Ойдағы.
Ең төменгі деңгейдегіге тірі болмаған материя жатады. Негізгі таңдау
принциптері болып, заттың, импульстың, энергияның және т.б. сақталу
заңдары жатады. Кез келген модельдеу сақталу заңдарын жазуда пайдаланатын
негізгі айнымалыларды таңдаудан басталады.
Сақтау заңдары жалғыз шешімдерді ерекшелемейді және барлық таңдаулар
принциптерін қамтиды. Түрлі шарттардың айырмашылығын білу ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.