Ляпунов сипаттаушы көрсеткіштері және біртекті сызықтық дифференциалдық жүйелердің орнықтығы


Мазмұны
Кіріспе . . .
І - тарау.
Қажетті анықтамалармен жалпы тұжырымдар.
§1 Функцияның сипаттаушы сандары . . .
§2 Сипаттаушы көрсеткіштердің негізгі қасиеттері . . .
§3 Сызықтың біртектес жүйе шешімдерінің сипаттаушы
көрсеткіштері . . .
ІІ- тарау
Дұрыс және келтірімді жүйелер.
§1 Дұрыс жүйелер . . .
§2 Үшбұрышты жүйелердің дұрыстығы. . Ляпунов теоремасы . . .
Мысалдар . . .
Әдебиеттер . . .
Кіріспе
Дифференциялдық теңдеу шешімінің сипатын анықтау үшін өзінің бірінші әдісіне Ляпунов шешемді бірсарынды (монотонды)
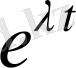 функциясымен салыстырады, мұндағы
функциясымен салыстырады, мұндағы
 - нақты сан. Мұндай салыстыру нәтижесінде әрбір шешімге белгілі бір
- нақты сан. Мұндай салыстыру нәтижесінде әрбір шешімге белгілі бір
 саны сәйкес қойылады. Егер
саны сәйкес қойылады. Егер
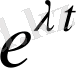 Функциялар жиынтығын өсу немесе кему кестесі ретінде алатын болса, онда осы кесте бойынша дифференциялдық теңдеулердің шешімдер жиынтығы реттелген болып шығады. Осылайша салыстыру негізінде Ляпунов сипаттаушы көрсеткіштер (сандар) теориясын жасаған. Ляпуновтың бірінші әдісі осы теорияға негізделген.
Функциялар жиынтығын өсу немесе кему кестесі ретінде алатын болса, онда осы кесте бойынша дифференциялдық теңдеулердің шешімдер жиынтығы реттелген болып шығады. Осылайша салыстыру негізінде Ляпунов сипаттаушы көрсеткіштер (сандар) теориясын жасаған. Ляпуновтың бірінші әдісі осы теорияға негізделген.
Жұмыста біртекті сызықты дифференциялдық теңдеулер жүйесінің негізгі кластарының біреуін құрайтын, дұрыс жүйелер қарастырылған.
Мұнда үшбұрышты жүйелер үшін негізгі теоремалардың бірі Ляпунов теоремасы және мысалдар келтірілген.
І-ТАРАУ: Қажетті анықтамалармен жалпы тұжырымдар
§1 Функцияның сипаттаушы сандары
Ляпуновтың анықтамасы.
Егер кез - келген мейлінше аз
 E>0 саны үшін нақты сан
E>0 саны үшін нақты сан
 мына теңдіктерді
мына теңдіктерді
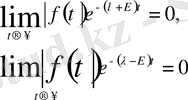 (1)
(1)
Қанағаттандыратын болса, онда оны
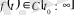 функциясының сипаттаушы көрсеткіші (саны) деп атайды.
функциясының сипаттаушы көрсеткіші (саны) деп атайды.
Бұл анықтамадан кез - келген функцияның сипаттаушы көрсеткіші бола бермейтіні көрініп тұр.
Перронның анықтамасы. Мына теңдік
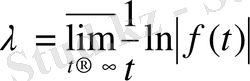 (2)
(2)
арқылы анықталатын
 саны (не
саны (не
 таңбасы)
таңбасы)
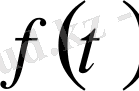 функциясының сипаттаушы көрсеткіші (саны) деп аталады.
функциясының сипаттаушы көрсеткіші (саны) деп аталады.
Ляпунов пен Перрон анықтамаларының өзара пара - пар екенін көрсетейік. (1) теңдіктер орындалсын. Оның біріншісінен
 санының бар болып, кез келген
санының бар болып, кез келген
 және
және
 үшін
үшін
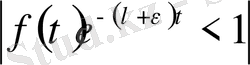 (3)
(3)
теңсіздігінің орындалатыны шығады. Ал екінші теңдік
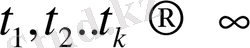 тізбегінің бар болып, ол үшін
тізбегінің бар болып, ол үшін
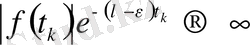 шартының орындалатынын білдіреді. Демек, жетерліктей үлкен
шартының орындалатынын білдіреді. Демек, жетерліктей үлкен
 үшін
үшін
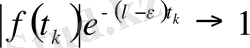 (4)
(4)
теңсіздігі орындалады.
(3) және (4) теңсіздіктері логорифмдеу арқылы
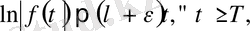
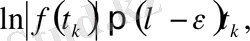
теңсіздіктерін аламыз. Бұл екі теңсіздік (2) формуланың дұрыстығын білдіреді. Енді сипаттаушы көрсеткіш (2) формула арқылы анықталсын. Онда
 саны табылып,
саны табылып,
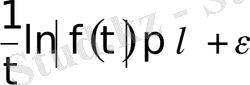 ,
,
 теңсіздігі ал
теңсіздігі ал
 {t
{t
 } тізбегі, t
} тізбегі, t
 табылып
табылып
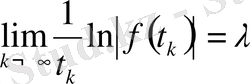 теңдігі алорындалады. Сондықтан
теңдігі алорындалады. Сондықтан
 үшін
үшін
 және
және
 Сандары табылып,
Сандары табылып,

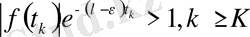
теңсіздіктері, яғни (2) орындалады.
(2) формула сипаттаушы көрсеткішті есептеу үшін өте ыңғайлы.
ЕСКЕРТУЛЕР.
- Жоғарыда айтылғандардың, үшін
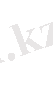 орындалғанда
орындалғанда
 Х{f}
Х{f}
 Equation. 3 болатыны, ал
Equation. 3 болатыны, ал
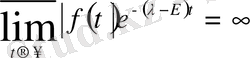
орындалғанда
,
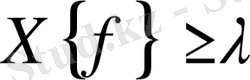 болатыны шығады. Демек,
болатыны шығады. Демек,
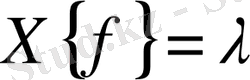 болса, онда
болса, онда
 кезде
кезде
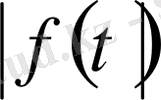 .
.
Функциясы кез-келген
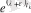 қарағанда баяуырақ және де белгілі бір
қарағанда баяуырақ және де белгілі бір
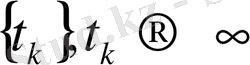 тізбегі бойынша
тізбегі бойынша
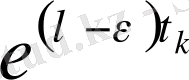 функциясынан тезірек өседі. (1- сурет) . Бұдан егер функцияның сипаттаушы көрсеткіші теріс болса, оның
функциясынан тезірек өседі. (1- сурет) . Бұдан егер функцияның сипаттаушы көрсеткіші теріс болса, оның
 кезде нөльге ұмтылатыны, ал сипаттаушы көрсеткіші оң болса, оның
кезде нөльге ұмтылатыны, ал сипаттаушы көрсеткіші оң болса, оның
 кезде шенелмегендігі шығады.
кезде шенелмегендігі шығады.
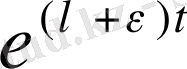
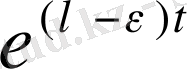
Егер де функцияның сипаттаушы көрсеткіші нөльге тең болатын болса, онда оның
 кездегі сипаты туралы ештеңе айтуға (с. к. бойынша) болмайды.
кездегі сипаты туралы ештеңе айтуға (с. к. бойынша) болмайды.
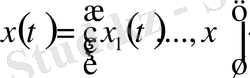
АНЫҚТАМА.
Үзіліссіз
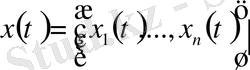
 вектор функциясының (матрица - жол немесе матрица - бағана) сипаттаушы көрсеткіші деп оның нормасының сипаттаушы көрсеткіші аталады.
вектор функциясының (матрица - жол немесе матрица - бағана) сипаттаушы көрсеткіші деп оның нормасының сипаттаушы көрсеткіші аталады.
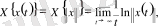 және де ол норманың қай түрі
және де ол норманың қай түрі
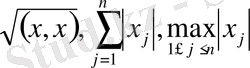 алынып тұрғанына байланысты болмайды, себебі ол нормалар өзара пара -пар.
алынып тұрғанына байланысты болмайды, себебі ол нормалар өзара пара -пар.
АНЫҚТАМА. Саны ақырлы функциялар жиынтығының сипаттаушы көрсеткіші деп олардың сипаттаушы көрсеткішінің ішіндегі ең үлкенін атайды.
Әлбетте, егер вектор - функцияны компоненттерінің жиынтығы есебінде қарастырып, оның сипаттаушы көрсеткіші
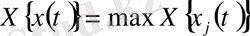 формуласы арқылы анықталса, онда ол
формуласы арқылы анықталса, онда ол
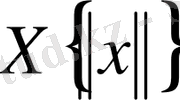 - мен тең болады.
- мен тең болады.
§2 Сипаттаушы көрсеткіштердің негізгі қасиеттері
1-Теорема.
Саны ақырлы функциялар
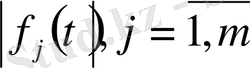 қосындысының сипаттаушы көрсеткіші осы функциялар көрсеткішінің (олар ақырлы болғанда ) ең үлкенінен аспайды. Ал егерде ең үлкен сипаттаушы көрсеткішке жалғыз ғана функция ие болса, қосындының көрсеткіші оған тең болады.
қосындысының сипаттаушы көрсеткіші осы функциялар көрсеткішінің (олар ақырлы болғанда ) ең үлкенінен аспайды. Ал егерде ең үлкен сипаттаушы көрсеткішке жалғыз ғана функция ие болса, қосындының көрсеткіші оған тең болады.
іргелі жүйені де нақты деп есептеуге болады.
ДӘЛЕЛДЕУІ: Формула түрінде жазғанда, теореманың 1- ші бөлігі мына теңсіздікті білдіреді.
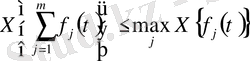 (1)
(1)
белгілеу енгізейік:
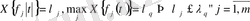
онда
 үшін
үшін
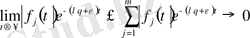

Бұдан (1) теңсіздіктің шығатыны айқын. Енді теореманың екінші бөлігін дәлелдейік.
 болсын. Онда
болсын. Онда
 үшін
үшін
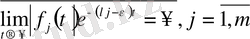
Еркін
 санын
санын
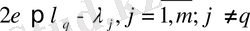 теңсіздігін қанағаттандыратындай етіп алайық. Онда
теңсіздігін қанағаттандыратындай етіп алайық. Онда
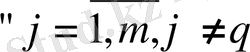 үшін
үшін
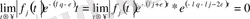
теңдігі орындалады. Сондықтан мына ақиқат теңсіздікті
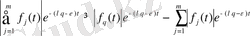
пайдалана отырып,
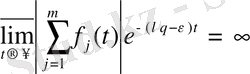
теңдігін аламыз. Олай болса,
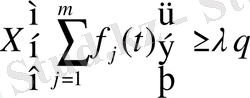 бұл теңсіздік (1) теңдікпен қосылып,
бұл теңсіздік (1) теңдікпен қосылып,
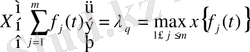
теңдігін береді.
Ескертулер.
1. Жасанды түрде қарағанда теорема кейбір функциялар ақырсыз
(
 неме-
неме-
се
 ) көрсеткішке ие болғанда да орындала береді.
) көрсеткішке ие болғанда да орындала береді.
2. Егер қосылғыштардың саны ақырсыз болатын болса, онда теорема мәнін жояды (орындалмайды)
2- Теорема. Саны ақырлы функциялар көбейтіндісінің сипаттаушы көрсеткіші осы функциялар көрсеткіштерінің қосындысынан аспайды,
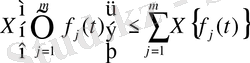 (2)
(2)
Дәлелдеуі. Әлбетте, мына тұжырым
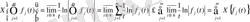
яғни, (2) орындалады.
Ескертулер.
Егер көбейткіш
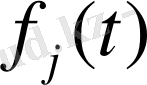 функцияларының арасында
функцияларының арасында
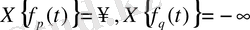 теңдіктерін қанағаттандыратын
теңдіктерін қанағаттандыратын
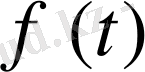 және
және
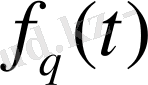 функциялары бар болса, онда (2) теңсіздік анықталмай қалады
функциялары бар болса, онда (2) теңсіздік анықталмай қалады
 .
.
Салдар. 1. Коэффициенттері шенелген ақырлы сызықтық тіркестің енетін функциялар көрсеткіштерінің ең үлкенінен аспайды.
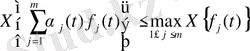 шынында да,
шынында да,
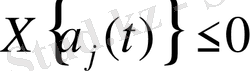
екенін ескере отырып, 1, 2 теоремар негізінде
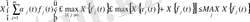
 Егерде сызықтық тіркестің коэффициенттері тұрақты болып, ал функциялардың біреуі ғана ең үлкен көрсеткішке ие болатын болса, онда тіркестің көрсеткіші сол үлкенге тең болады. (1-теореманы дәлелдегендей) :
Егерде сызықтық тіркестің коэффициенттері тұрақты болып, ал функциялардың біреуі ғана ең үлкен көрсеткішке ие болатын болса, онда тіркестің көрсеткіші сол үлкенге тең болады. (1-теореманы дәлелдегендей) :
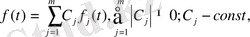
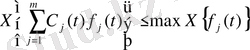
3-Теорема.
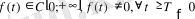 функциясымен оның кері функциясы көрсеткіштерінің қосындысы нөлге тең болуы үшін
функциясымен оның кері функциясы көрсеткіштерінің қосындысы нөлге тең болуы үшін
 кезде
кезде
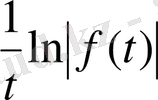 өрнегінің ақырлы шегі болуы қажетті де жеткілікті.
өрнегінің ақырлы шегі болуы қажетті де жеткілікті.
Дәлелдеуі.
Егер
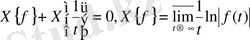
болса, онда мына теңдікке
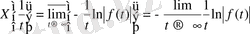
сүйеніп,
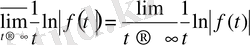
теңдігін аламыз, яғни анықталған ақырлы шек
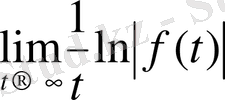 бар болады. Егер
бар болады. Егер
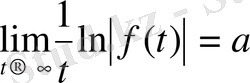 бар болса, онда
бар болса, онда
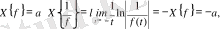 яғни
яғни
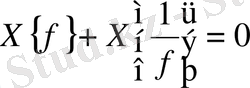 орындалады.
орындалады.
1-Анықтама.
Егер
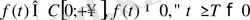 үшін ақырлы шек
үшін ақырлы шек
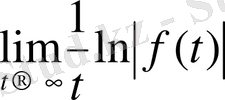
бар болса, онда
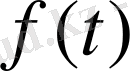 функциясының көрсеткішін дәл көрсеткіш деп атайды.
функциясының көрсеткішін дәл көрсеткіш деп атайды.
4 теорема. Егер функция f(t) дәл көрсеткішке ие болса онда f(t) және g(t) ∈С[0; ∞ функциялар көрсеткіштерінің қосындысына тең болады.
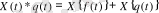 (3)
(3)
Дәлелдеуі.
2 -теорема негізінде
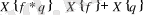 (4)
(4)
болады. Екінші жағынан 3- теореманы ескере отырып, осы 2- теореманы қайта қолдансақ
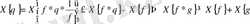
теңсіздігін аламыз. Ол (4) теңсіздікпен қосылып, (3) теңдікті береді.
Енді көрсеткіштік функция
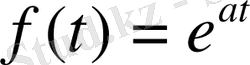 қарастырайық. Оның интегралы (алғашқы бейнесі)
қарастырайық. Оның интегралы (алғашқы бейнесі)
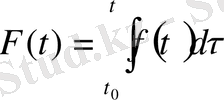 түрінде алынсын.
түрінде алынсын.
Егер
 болса,
болса,
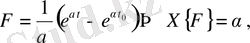 Ал
Ал
 болғанда,
болғанда,
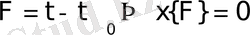 яғни
яғни
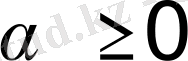 болғанда
болғанда
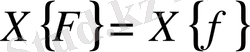 болады.
болады.
Егер де
 болса, онда
болса, онда
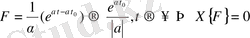 болады да
болады да
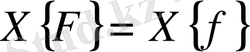 теңдігі орындалмайды. Алайда бұл жағдайда интегралды
теңдігі орындалмайды. Алайда бұл жағдайда интегралды
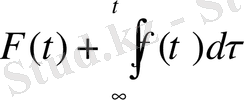 түрінде алатын болса,
түрінде алатын болса,
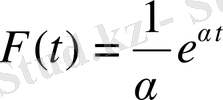 болар еді, теңдік сақталар еді.
болар еді, теңдік сақталар еді.
Сондықтан Ляпунов интегралдың мынандай ұғымын енгізген.
2- Анықтама.
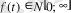 функциясының интегралы деп мына формулалар
функциясының интегралы деп мына формулалар
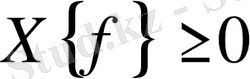 кезде
кезде
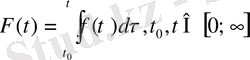
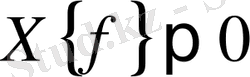 кезде
кезде
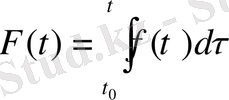 арқылы анықталатын
арқылы анықталатын
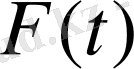 функциясын атайды.
функциясын атайды.
§3 Сызықтық біртектес жүйе шешімдерінің сипаттаушы көрсеткіштері
Сызықтық біртектес
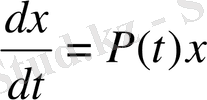 (1)
(1)
дифференциялдық жүйесін қарастырайық. Мұнда
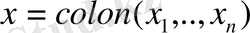 ал нақты матрица
ал нақты матрица
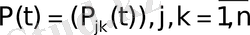 үзіліссіз:
үзіліссіз:
 . Әлбетте (1) жүйесінің нөлдік шешімі
. Әлбетте (1) жүйесінің нөлдік шешімі
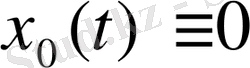 бар. Оның сипаттаушы көрсеткіші
бар. Оның сипаттаушы көрсеткіші
 -ке тең.
-ке тең.
1-ТЕОРЕМА.
Егер (1) жүйенің коэффициент матрицасы
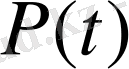 шенелген болса, онда жүйенің кез келген нөлден өзгеше шешімі ақырлы көрсеткішке ие болады.
шенелген болса, онда жүйенің кез келген нөлден өзгеше шешімі ақырлы көрсеткішке ие болады.
Дәлелдеуі.
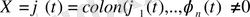 (1) жүйенің кез келген шешімі болсын. Теореманың шарты бойынша
(1) жүйенің кез келген шешімі болсын. Теореманың шарты бойынша
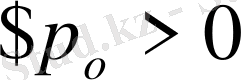
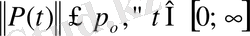 орындалады. Әлбетте,
орындалады. Әлбетте,
 шешімін мына түрде
шешімін мына түрде
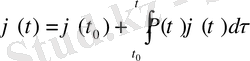 жазуға болады. Бұдан норма бойынша бағалау арқылы
жазуға болады. Бұдан норма бойынша бағалау арқылы
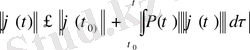

Гронуолл леммасына сүйеніп
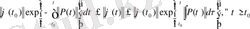
теңдігі алынады. Ал бұдан
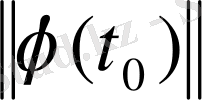 саны нөлге тең дәл көрсеткішке ие болғандықтан,
саны нөлге тең дәл көрсеткішке ие болғандықтан,
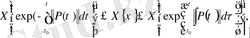
яғни
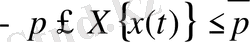 теңсіздіктері шығады. Мұндағы
теңсіздіктері шығады. Мұндағы
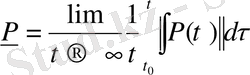 ;
;
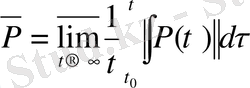 енді
енді
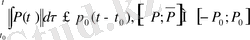 екенін ескерсек, (1) жүйенің нөлге тең емес шешімдерінің сипаттаушы көрсеткіштері
екенін ескерсек, (1) жүйенің нөлге тең емес шешімдерінің сипаттаушы көрсеткіштері
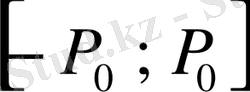 кесіндісіне жататыны алынады.
кесіндісіне жататыны алынады.
Ескерту. Жүйененің коэффициенттерінің шенелген болуы шешуші шарт. Ол бұзылса теорема орындалмайды.
Лемма. Әр түрлі (бір - біріне тең емес) көрсеткіштерге ие вектор - функциялар өзара сызықтық тәуелсіз болады.
Дәлелдеуі.
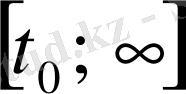 аралығында анықталған
аралығында анықталған
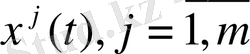 вектор - функциялары берілсін және
вектор - функциялары берілсін және
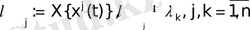
 болсын. Анықтық үшін
болсын. Анықтық үшін
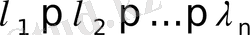 деп есептейік. Кері жорып, бәрі бірдей нөл емес
деп есептейік. Кері жорып, бәрі бірдей нөл емес
 сандары табылып,
сандары табылып,
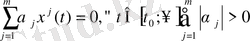 орындалсын делік. Коэффициенттердің ішінде
орындалсын делік. Коэффициенттердің ішінде
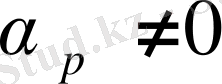 болсын. Онда
болсын. Онда
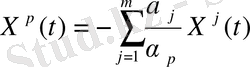
§2 - дәлелденген 1-2 теореманың салдарына сүйеніп,
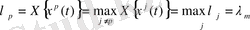
теңдігін аламыз. Бұл шартқа қайшы. Кері жору қате,
 сызықтық тәуелсіз.
сызықтық тәуелсіз.
3-Теорема.
Жүйенің ерекше көрсеткіші
 болса, онда кез келген
болса, онда кез келген
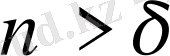 саны үшін
саны үшін
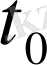 мен
мен
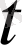 - дан тәуелсіз әрі мына теңсіздікті қанағаттандыратын
- дан тәуелсіз әрі мына теңсіздікті қанағаттандыратын
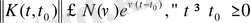 (2)
(2)
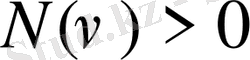 саны табылады.
саны табылады.
Дәлелдеуі.
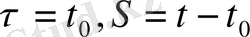 деп алсақ,
деп алсақ,
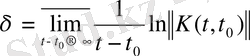
теңдігі алынады. Бұдан
 немесе
немесе
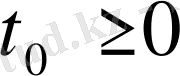 үшін
үшін
 саны табылып,
саны табылып,
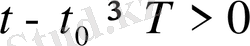 болғанда,
болғанда,
 (3)
(3)
теңсіздігі алынады. Ал
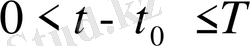 болғанда,
болғанда,
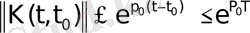
орындалады. Демек,
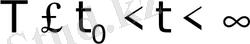 немесе
немесе
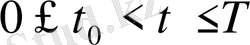 кезде
кезде
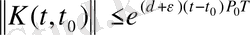 (4)
(4)
теңсіздігі орындалады.
Ал мына
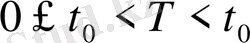 кезде
кезде

теңсіздігі орындалады. Егер
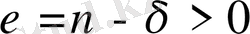 деп, ал
деп, ал
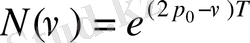 деп белгілесек (4), (5) теңсіздіктерден (3) теңсіздік шығады. Сонымен ерекше көрсеткіш (3) теңсіздікті қанағаттандыратын барлық
деп белгілесек (4), (5) теңсіздіктерден (3) теңсіздік шығады. Сонымен ерекше көрсеткіш (3) теңсіздікті қанағаттандыратын барлық
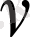 сандарының ең кішісі (төменгі шегі) болып табылады және (1) жүйенің бірқалыпты
сандарының ең кішісі (төменгі шегі) болып табылады және (1) жүйенің бірқалыпты
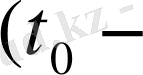 ден тәуелсіз) орнықтылығын анықтайды.
ден тәуелсіз) орнықтылығын анықтайды.
 кезде (1) жүйе бірқалыпты асимптотикалық орнықты болады. Егер (1) - жүйе
кезде (1) жүйе бірқалыпты асимптотикалық орнықты болады. Егер (1) - жүйе
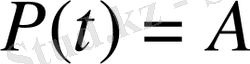 болады. Жалпы
болады. Жалпы
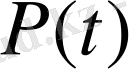 айнымалы матрица болғанда, мұндай қатынас алынбайды.
айнымалы матрица болғанда, мұндай қатынас алынбайды.
 кеңістігінде сызықтық біртектес
кеңістігінде сызықтық біртектес
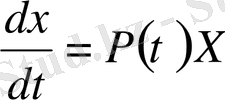 (1)
(1)
 жүйесін қарастырайық. оның спектрі өсу бағытында орналасқан
жүйесін қарастырайық. оның спектрі өсу бағытында орналасқан
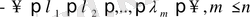 болсын. (1) жүйенің барлық шешімдерінің жиынтығы сызықтық кеңістік
болсын. (1) жүйенің барлық шешімдерінің жиынтығы сызықтық кеңістік
 құрайтыны белгілі. Ол кеңістіктің нүктелері болып жеке
құрайтыны белгілі. Ол кеңістіктің нүктелері болып жеке
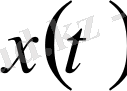 шешімдері, ал базисы болып шешімдердің кез - келген ілгері жүйесі
шешімдері, ал базисы болып шешімдердің кез - келген ілгері жүйесі
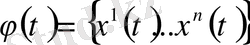 табылды. Ілгері жүйеге енетін, сипаттаушы көрсеткіштері
табылды. Ілгері жүйеге енетін, сипаттаушы көрсеткіштері
 - ге тең, шешімдердің саны
- ге тең, шешімдердің саны
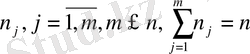 болсын. Мұнда кейбір
болсын. Мұнда кейбір
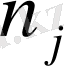 - лер нөлге тең болуыда мүмкін. Онда
- лер нөлге тең болуыда мүмкін. Онда
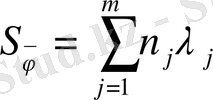
 жүйесінің сипаттаушы көрсеткіштерінің қосындысы деп аталады. Оның төменгі шегін анықтайтын Ляпунов теңсіздігі дәлелденді:
жүйесінің сипаттаушы көрсеткіштерінің қосындысы деп аталады. Оның төменгі шегін анықтайтын Ляпунов теңсіздігі дәлелденді:
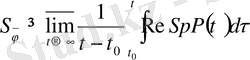 (2)
(2)
сипаттаушы көрсеткіштері
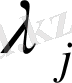 болатын өзара сызықтық тәуелсіз шешімдердің ең үлкен саны
болатын өзара сызықтық тәуелсіз шешімдердің ең үлкен саны
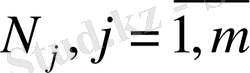 болсын. Сипаттаушы көрсеткіштері
болсын. Сипаттаушы көрсеткіштері
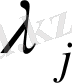 - ден аспайтын, нөлдік шешімді қамтитын барлық шешімдер жиынтығы
- ден аспайтын, нөлдік шешімді қамтитын барлық шешімдер жиынтығы
 арқылы белгіленсін.
арқылы белгіленсін.
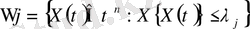 Әлбетте,
Әлбетте,
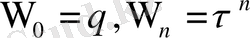 . қосындымен көбейтіндінің көрсеткіштері туралы теоремалардан мына қасиеттер алынады.
. қосындымен көбейтіндінің көрсеткіштері туралы теоремалардан мына қасиеттер алынады.
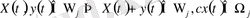
сондықтан
 жиынтығы
жиынтығы
 кеңістігінің ішкі сызықтық кеңістігі болып табылады.
кеңістігінің ішкі сызықтық кеңістігі болып табылады.
1 - Лемма.

 Кеңістігінің өлшемі
Кеңістігінің өлшемі
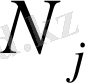 ге тең болады.
ге тең болады.
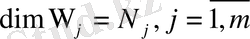 (3)
(3)
Дәлелдеуі.
Шынында да, анықтама бойынша, сипаттаушы көрсеткіші
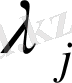 болатын әрбір шешім
болатын әрбір шешім
 - ге енеді. Демек,
- ге енеді. Демек,
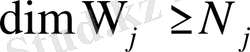 (4)
(4)
енді
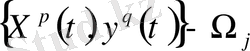 кеңістігінің
кеңістігінің
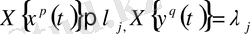
шартын қанағаттандыратын базисы болсын. Бұл базис міндетті түрде ең үлкен көрсеткішке
 ие шешімді өзіне ұстайды. Олай болмаса базистық шешімдердің сызықтық тіркесі (комбинациясы) арқылы өрнектелмейтін шешімдер бар болар еді. (1) жүйенің сипаттаушы көрсеткіші
ие шешімді өзіне ұстайды. Олай болмаса базистық шешімдердің сызықтық тіркесі (комбинациясы) арқылы өрнектелмейтін шешімдер бар болар еді. (1) жүйенің сипаттаушы көрсеткіші
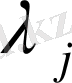 - ге тең.
- ге тең.
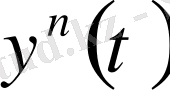 шешімін алайық. Онда
шешімін алайық. Онда
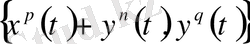 шешімдер жиынтығы жаңа базаис құрайды. Шынында да, егер
шешімдер жиынтығы жаңа базаис құрайды. Шынында да, егер
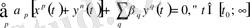
тепе - теңдігін қарастыратын болсақ, онда оны мына түрде
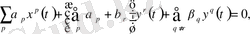
қайта жазып,
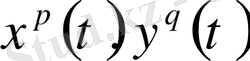 шешімдерінің сызықтық тәуелсіздігі арқасында
шешімдерінің сызықтық тәуелсіздігі арқасында
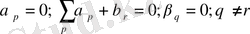 теңдіктерін алар едік. Бұдан
теңдіктерін алар едік. Бұдан
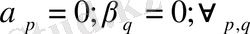 алынады. Олай болса,
алынады. Олай болса,
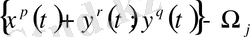 кеңістігінің жаңа базисы. Бұл базистың әрбір элементі (шешімдер)
кеңістігінің жаңа базисы. Бұл базистың әрбір элементі (шешімдер)
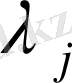 сипаттаушы көрсеткіштергге ие. Демек,
сипаттаушы көрсеткіштергге ие. Демек,
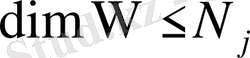 (5)
(5)
(4), (5) теңсіздіктерін (2) теңдік алынады.
1-Салдар. Мына теңсіздіктер орындалады:
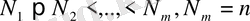
2-Салдар.
Кез келген
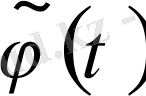 іргелі жүйесіне енетін, сипаттаушы көрсеткіші
іргелі жүйесіне енетін, сипаттаушы көрсеткіші
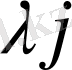 болатын шешімдер саны
болатын шешімдер саны
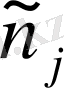 үшін
үшін
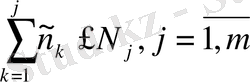 (6)
(6)
теңсіздігі орындалады.
Шынында да, сипаттаушы көрсеткіштері
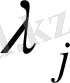 - ден аспайтын шешімдерді қамтитын
- ден аспайтын шешімдерді қамтитын
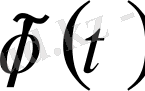 жүйесінің кез келген бөлігі
жүйесінің кез келген бөлігі
 кеңістігінде жатады.
кеңістігінде жатады.
1-Анықтама.
Кез келген
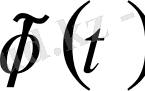 іргелі жүйесімен салыстырғанда сипаттаушы көрсеткіштердің ең кіші қосындысына ие болатын
іргелі жүйесімен салыстырғанда сипаттаушы көрсеткіштердің ең кіші қосындысына ие болатын
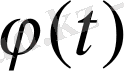 іргелі жүйесі шешімдердің қалыпты іргелі жүйесі деп аталады.
іргелі жүйесі шешімдердің қалыпты іргелі жүйесі деп аталады.
Егер
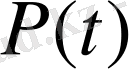 матрицасы нақты болса, онда әрбір сипаттаушы көрсеткіш үшін, оған ие болатын нақты шешім бар болады. Сондықтан бұл жағдайда қалыпты тргелі жүйені де нақты деп есептеуге болады.
матрицасы нақты болса, онда әрбір сипаттаушы көрсеткіш үшін, оған ие болатын нақты шешім бар болады. Сондықтан бұл жағдайда қалыпты тргелі жүйені де нақты деп есептеуге болады.
2-Анықтама. Шешімдердің қалыпты іргелі жүйесінің көрсеткіштері (1) дифференциалдық жүйенің сипаттаушы көрсеткіштері деп аталады.
Мысалдар
Мысал 1.
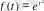 көбейтінді
көбейтінді
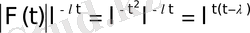
кез келген ақырлы
 үшін
үшін
 кезде шенелмеген. Ал, керісінше, егер
кезде шенелмеген. Ал, керісінше, егер
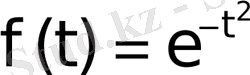 болса,
болса,
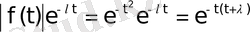
кез келген ақырлы
 үшін
үшін
 кезде нөлге ұмтылады. Демек, мынадай жағдайлар болуы мүмкін. Кез келген ақырлы
кезде нөлге ұмтылады. Демек, мынадай жағдайлар болуы мүмкін. Кез келген ақырлы
 үшін
үшін
 болуы мүмкін. Онда
болуы мүмкін. Онда
 функциясының сипаттаушы көрсеткіші үшін
функциясының сипаттаушы көрсеткіші үшін
 таңбасы алынады. Егерде кез келген ақырлы
таңбасы алынады. Егерде кез келген ақырлы
 үшін
үшін
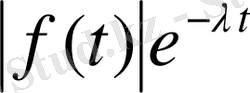 көбейтіндісі
көбейтіндісі
 кезде шенелмеген болса, онда
кезде шенелмеген болса, онда
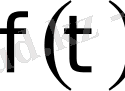 функциясының сипаттаушы көрсеткіші үшін
функциясының сипаттаушы көрсеткіші үшін
 таңбасы алынады. Мұндай толықтыру қабылдағанда, кез келген үзіліссіз функция ақырлы немесе ақырсыз сипаттаушы көрсеткішке ие болады.
таңбасы алынады. Мұндай толықтыру қабылдағанда, кез келген үзіліссіз функция ақырлы немесе ақырсыз сипаттаушы көрсеткішке ие болады.
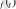 функциясының сипаттаушы көрсеткіші қысқаша
функциясының сипаттаушы көрсеткіші қысқаша
 таңбасымен белгіленеді.
таңбасымен белгіленеді.
Мысал 2.
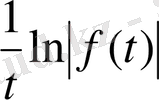 өрнегі
өрнегі
 кезде белгілі бір шекке ұмтылатын болса, ол шек
кезде белгілі бір шекке ұмтылатын болса, ол шек
 функциясының сипаттаушы көрсеткіш болып табылады. Бұдан, дербес жағдайда, дәрежелік функция мен нөлден өзгеше тұрақтының сипаттаушы көрсеткішке нөлге тең болатыны көрініп тұр. (2) формуладан сипаттаушы көрсеткіш бірсарындылық қасиетке ие екендігі шығады, яғни егер
функциясының сипаттаушы көрсеткіш болып табылады. Бұдан, дербес жағдайда, дәрежелік функция мен нөлден өзгеше тұрақтының сипаттаушы көрсеткішке нөлге тең болатыны көрініп тұр. (2) формуладан сипаттаушы көрсеткіш бірсарындылық қасиетке ие екендігі шығады, яғни егер
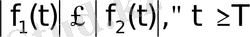 болса, онда
болса, онда
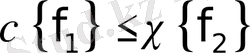 екендігі алынады. Сондықтан бірқалыпты шенелген кез келген функцияның сипаттаушы көрсеткіш нөлден аспайды. әлбетте кез келген
екендігі алынады. Сондықтан бірқалыпты шенелген кез келген функцияның сипаттаушы көрсеткіш нөлден аспайды. әлбетте кез келген
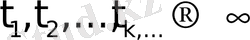 тізбегі үшін
тізбегі үшін
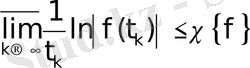 теңсіздігі орындалады.
теңсіздігі орындалады.
Мысал 3.
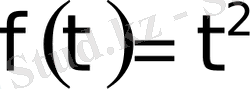 және
және
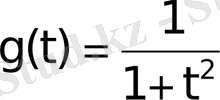 функциясының сипаттаушы көрсеткіш нөлге тең. Алайда
функциясының сипаттаушы көрсеткіш нөлге тең. Алайда
 кезде олардың біріншісі шексіздікке, екіншісі нөлге ұмтылады.
кезде олардың біріншісі шексіздікке, екіншісі нөлге ұмтылады.
Егер
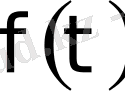 функцияның сипаттаушы көрсеткіш
функцияның сипаттаушы көрсеткіш
 болса, онда кез келген
болса, онда кез келген
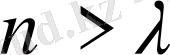 саны үшін
саны үшін
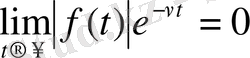 теңдігі, ал кез келген
теңдігі, ал кез келген
 үшін
үшін
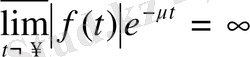 теңдігі орындалады.
теңдігі орындалады.
Мысал 4
1) нөлден өзгеше кез келген тұрақтының сипаттаушы көрсеткіш нөлге тең, ал нөлдің сипаттаушы көрсеткіші
 - ке тең. Себебі
- ке тең. Себебі
 үшін
үшін
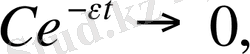
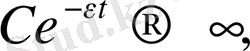

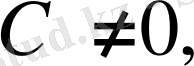
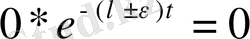
2) Коэффициенттері тұрақты көпмүшеліктің сипаттаушы көрсеткіш нөлге тең. Себебі көрсеткіштік функция
 кезде дәрежелік функцияға қарағанда тезірек өседі не кемиді:
кезде дәрежелік функцияға қарағанда тезірек өседі не кемиді:

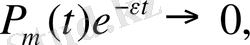

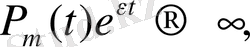

3) егер
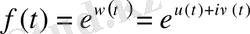 болса, онда
болса, онда
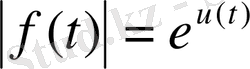 болғандықтан,
болғандықтан,
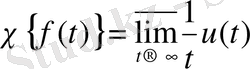
4)


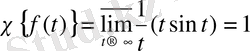
Ляпуновтың анықтамасы бойынша сесптесек,
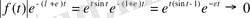

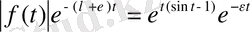

кезде шенелген.
Мысал 5.
 функциясын беретін ақырсыз қосындысы (қатарды) қарастырайық:
функциясын беретін ақырсыз қосындысы (қатарды) қарастырайық:
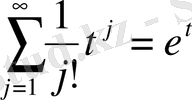
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz