Полимерлердегі крип құбылысының термофлуктуациялық моделі және күйреу деңгейін анықтау


Мазмұны
Кіріспе . . . 4
- Кернеу релаксациясын моделдеу . . . 5
1. 1 Феноменологиялық модель . . . 5
1. 2 Кинетикалық модель . . . 10
1. 3 Молекулалық құрылым бойынша есеп . . . 11
1. 4 Есептеулер нәтижесі . . . 12
2. Крип құбылысының термофлуктуациялық мо делін жасау . . . 13
2. 1 Амофты қабаттағы крип құбылысының моделін жасау . . . 13
2. 2 Сандық есептеу алгоритмі . . . 16
2. 3 Сандық моделдеу нәтижелері . . . 17
3. Күйреу деңгейін анықтау . . . 17
Қорытынды . . . 18
Қолданылған әдебиеттер . . . 19
Қосымша 1 . . . 20
Қосымша 2 . . . 26
Реферат
Бұл «Крип құбылысының термофлуктуациялық моделі» деп аталатын магистрлік дисертиция 30 беттен тұрады. Жұмыс кіріспеден, негізгі үш бөлімнен және қорытынды мен екі қосымшадан тұрады.
Қазіргі уақытта конструкциялық полимерлердің кең қолданыста болуына байланысты оларды зерттеу, яғни конструкциялық полимерлер мен олардың қосылысынан жасалған материалдардың мықтылығын, бұзылу шарттарын, төзімділік уақытын болжау актуальды мәселе болып отыр. Соның ішінде жылдам дамып, толық зерттеліп бітпеген бір саласы материалдар бұзылуының термофлуктуациялық теориясы [1] .
Бұл жұмыста кейбір аспектлерге қатысты жаңа болып табылатын криптің термофлуктуациялық моделі мен полимерлердің күйреу деңгейі анықталады. Алынған теңдеулерді шешуге арналған итерациялық алгоритм жасалды.
1 қосымшада фортран тілінде жазылған модель теңдеулерін шешіп, күйреу деңгейін есептеуге арналған программаның мәтіні берілген.
2 қосымшада магистрлік жұмыстың негізгі нәтижелерінің бірі болып табылатын деформация мен температураның әртүрлі мәндеріндегі крип қисық-тарының графиктері берілген.
Жалпы диссертациялық жұмыстағы негізгі терминдер мыналар: крип, кернеу, температура, деформация, күйреу деңгейі, полимер, амофты қабат т. б.
Кіріспе
Жүктелген қатты денелердің бұзылуы туралы қазіргі ілім (оны болжамдау міндеттердің шешіміне тәсіл белгілеуші) өзінің принциапиалды негізінде де аяқталмаған - табиғаты мен бұзылуға жауапты элементарлық жағдайлардың критерилары айқындалмаған.
Ұзақ жүктеу жағдайларында полимерлердің бұзылуына арналған зерттеулер қазіргі уақытта қатты дене механикасының жеке бағытын құрады [1-6] .
Термофлуктуациялық бұзылу теориясы негізінде [4-7] - де жылжу жағдайларда полимердің бұзылуына дейін уақытты болжамдау жөніндегі классикалық қорытындылар жасалған. Ұзақ уақытқа төзімділік үшін негізгі ара қатынастар бөліну активациясы энегриясының терминдарында және қоса берілген кернеуде қалыптасады [1] .
Микроскопикалық мөлшерлерден және желілерде жүктемені кездейсоқ бөлінуіне байланысты материалдың макроскопикалық сипаттамалары формулалардың параметрлері болып табылады [8-9] .
Термофлуктациялық теорияның шеңберінде тізбек микродеформациясынан және көршілес түйірлердің өзара әрекетінен бастап функцияларында [10] полимер тізбегінің жеке бойлы деформацияланған учаскесінің ұзақ мерзімділігі үшін формула алынған. Қорытындылар [10] статистикалық физиканың классикалық ұсыныстарына сүйенеді. Сонымен қатар полимер тізбегінің үш көршілес учаскелерінің ұзындығының жылулық флуктуациялары ескеріледі.
Негізгі жеңілдететін жағдай [10] - 4 жүйелі түйірлерден құрылған учаскесінің ұзындығы тұрақты деп болжамдалады.
Осы жұмыста қорытындыда [10] және «Регель элементі» түрінде аморфты жұқа қабатты модельді көрінісінде негізделген аморфты-кристалдық полимерде жылжу бұзулығы мен деформациясының есебі ұсынылады [7-9] .
Полимерлердің механикалық қасиеттері бойынша елеулі ерекшеленетін кристаллды және аморфты фазалардан құрылған күрделі молекулалық құрылым бар екені мәлім [11] .
Кернеу релаксациясы кезінде бұзылу аморфты фазада болады және ұзақтығы бойынша бірнеше түрлі стадиялар бар [12, 13] .
Полимерлердің механикалық қасиеттері көптеген қатынастарда металлдардың қасиеттерінен ерекшеленеді. Осы айырмашылықтардың көптеген түрі материалдардың осы екі класының құрылымына тән ерекшеліктерімен байланыстыруға болады. Полимерлердің негізгі қасиеті - олардың молекулалары ковалентті байланған атомдардың ұзын тізбегі болып табылады. Жай мысалдардың бірі - полиэтилен, оның молекулалары қайталанатын -СН 3 бірліктерден құрылады, оны -СНа=СНа- этиленнің полимеризациясы арқылы алады.
Поликонденсациялық полимерлерді су шығару арқылы бифункционалды молекулалардың өзара әрекет ету кезінде алады, оларға, мысалы полиэтилентерафталат және нейлон жатады.
Осының бәрі сызықты полимерлердің мысалы, мұнда мономерлы звенолары үзілмейтін «жіп» құрайды және де әр молекулалық тібек химия тұрғысында басқаларымен байланысты емес. Бұдан да күрделі құрылымдар кездеседі. Кейбір полимерлердің тізбектері бір бірімен брнеше жерлерде қосылған және де торлы құрылым құрайды.
Басты тізбектің бірнеше жерлерінен екінші тізбектер басталуы сияқты тізбектің тармақтануы құрылымды күрделендірудің тағы бір жағдайы болып табылады.
Бірінші тарауда релаксацияның негізгі модельдері, екінші тарауда - жылжу модельдері, үшіншіде - ұзақ мерзімдік үшін формулалардың шолуы суреттелген.
1. Кернеу релаксацияны моделдеу
- 1 Феноменологиялық модельдер
«Кернеу релаксациясы» термині денеде оның тұрақты деформациясы кезінде механикалық кернеудің азаю құбылысына қолданылады. Бірақ та, релаксациялық құбылыстар өзгеріп отыратын механикалық кернеу кезінде де болады. Бұдан басқа, релаксация механикалық кернеу кезінде ғана емес, сондай-ақ электрикалық, магниттік және басқа да құбылыстар кезінде жүзеге асырылады. Бұл жерде механикалық релаксациясы, яғни механикалық кернеу релаксациясын қаралуымен шектелейік. Кернеудің қисық релаксациясын суреттеу үшін деформация заңдарының дифференциалды және интегралды тәуелділігінде құрылған түрлі теориялар бар. Кернеу мен деформация арасында тәуелділікті белгілеп, уақыт бойынша деформацияны тұрақты деп есептей отырып, кернеу релаксациясының өту заңын алады. Деформациялауды орнату үшін түрлі тәсілдер бар:
- Модельдік ұсыныстар негізінде [1-6, 16] дифференциалды теңдеу алу.
- Аргументтің ағымдағы мағынасын ғана емес, сондай-ақ деформалаудың бүкіл тарихын ескеретін мұралық типтің [7-10] теңдеуінде негізделетін интегралды теңдеу алу.
- Жылжудың техникалық теориясы негізінде деформация мен кернеу, олардың өзгеру жылдамдығы мен уақыты арасында функционалды тәуелділік алу [11-14] .
Феноменологиялық теориялар, оның ішінде жылжу теориясы суреттелген процесстерді толық сипаттай алмайтыны бәрімізге мәлім. Есеп пен сараптаудың сәйкесуі әрқашан да толық емес болып қалады. Сндықтан да, түрлі теориялардың нәтижелілігін бағалау есеп пен сараптау қортындылар айырмашылығының анализінде негізделеді.
Ең алдымен, теория болжамдау және алдына алу көрудің құралы болуы керек [15], ал теңдеудің коэффициентерінің физикалық мағынасы болуы керек . Төменде кернеу релаксациясының түрлі теорияларын қарайық.
Мұралықтың сызықтық теориясы. Мұралықтың сызықты теориясы механикалық полимерлік материалдарды суреттеу кезінде кеңінен таралған. Анықтамасы бойынша сызықты тұтқыр серпімді дене төменде келтірілген теңдікті қанағаттандыру керек:

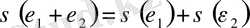 (1. 1)
(1. 1)
мұнда с - тұрақты өлшем,
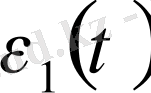 және
және
 - t уақытында деформацияның өзгеру заңдары.
- t уақытында деформацияның өзгеру заңдары.
(1. 1) шартын біртектілік шарты, ал (1. 2) - сызықты суперпозиция принципінің математикалық формуласы деп атайды. Суперпозицияның принципіне сәйкес Больцман [7] сызықты теория ұсынған. Бұл теорияда интегралды теңдеуді қолдана отырып, бір осьті жүктеу кезіндегі кернеу мен деформация арасындағы байланыстың мынадай түрі бар:
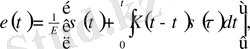 (1. 2)
(1. 2)
 (1. 3)
(1. 3)
мұнда Е - серпімділіктің кенеттік модулі,
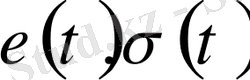 -
t уақытын кезеңіндегі деформация мен кернеу,
-
t уақытын кезеңіндегі деформация мен кернеу,
 - ағымдағы уақыт, К
- ағымдағы уақыт, К
 және R
және R
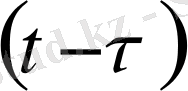 - бірқалыпты азаятын функцияның мұралық өзегі, К
- бірқалыпты азаятын функцияның мұралық өзегі, К
 - теңдеудің өзегі (1. 3),
- теңдеудің өзегі (1. 3),
R
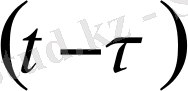 ал функциясы - оның резольвенті.
ал функциясы - оның резольвенті.
Белгілі бір функцияның негізінде басқа функцияны белгілеуге мүмкіндік беретін (1. 3) және (1. 4) типтегі сызықты интегралды теңдеуді шешуі әдістері, сондай-ақ К
 және R
және R
 функциялары арасындағы байланыстар жұмыстарды суреттелген.
функциялары арасындағы байланыстар жұмыстарды суреттелген.
Бұдан басқа, [3] -те (1. 3) теңдеуді жазудың басқа нысаны бар, ол
 кезінде төменде келтірілген релаксация түрінің теңдеуіне сәйкеседі:
кезінде төменде келтірілген релаксация түрінің теңдеуіне сәйкеседі:
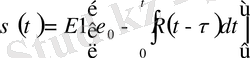 (1. 4),
(1. 4),
(1. 3) және (1. 4) теңдеулердің айырмашылығы релаксация өзегінің өлшемділігіне байланысты.
Осы теңдеулер бойынша, гер де интегралды теңдеудің (1. 4) өзгеі белгілі болса, кернеудің қисық релаксациясы құрылуы мүмкін.
Теңдеуді дифференциялай (1. 4) отырып, R(t) релаксация жылдамдығына пропорционалды екенін көреміз.
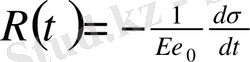 (1. 5)
(1. 5)
Сонымен, R(t) функциясын белгілеу үшін сараптау түрде белгіленген функциялардың дифференциялануы қажет. Бірақ та, осындай операция мәнді болып табылатын үлкен қателікке ұшыратады. Көрсетілген кемшілікті жою үшін ең алдымен өзек теңдігінің аналитикалық формасы беріледі, ал тәжірибеден теңдеуге жататын параметрлер ғана белгіленеді.
Вольтер [10] типтегі сызықты уақытша операторларды енгізетін болсақ, Больцманның теңдеуін қысаң нысанда жазуға болады:
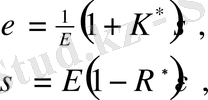 (1. 6)
(1. 6)
Мұнда,
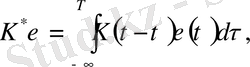
 функциясы оператордың өзегі болып табылады,
функциясы оператордың өзегі болып табылады,
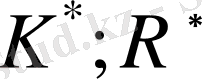 - Вольтерр операторының рұқсат етілетін функциясы немесе резольвенті. Символикалық теңдеуді (1. 5) және (1. 6) былай жазуға болады.
- Вольтерр операторының рұқсат етілетін функциясы немесе резольвенті. Символикалық теңдеуді (1. 5) және (1. 6) былай жазуға болады.
 (1. 7)
(1. 7)
Осы теңдеулер сыртынан Гука заңына ұқсас, бірақ та Работнов [10] қабылдаған терминологияға сәйкес оларды мұралық серпімділік заң деп атауға болады.
Жылжу және релаксация функциясының негізінде [4] мынадай теңдеу шығаруға болады:
 (1. 8)
(1. 8)
Бұл үйірткі типтегі интегралдармен ара қатынасты белгілейтін Стилтьес үйірткі типтегі интегралдар болып табылады. Оларды жүктеме кенеттен салынған немесе деформация кенеттен пайда болған кезде ыңғайлы қолдануға болады.
(1. 6) және (1. 7) теңдеуінен (1. 3) және (1. 4) интегралды теңдеуіне ауысу ықпалдасуды бөлшектеу бойынша жүзеге асырылады
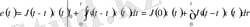 (1. 9)
(1. 9)
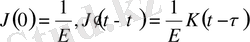 белгілеп, (1. 9) теңдеу шығарамыз.
белгілеп, (1. 9) теңдеу шығарамыз.
(1. 8) теңдеуді бөлшектеп ықпалдастыра отырып, мынаны шығарамыз:
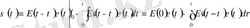 (1. 10)
(1. 10)
 белгілеп (1. 11) теңдеуін шығарамыз.
белгілеп (1. 11) теңдеуін шығарамыз.
- Кинетикалық модель
1. Созылудың тұрақты деформациясы жағдайларында полимердің аморфты қабатының бұзылуын қарайық. [7-9] сияқты түры ұзындығы бар және соңы кристаллиталарда бекітілген тізбектер элементтер болып табылады.
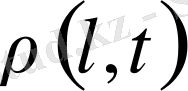 -ұзындығы бойынша тізбектерді бөлу тығыздығы,
-ұзындығы бойынша тізбектерді бөлу тығыздығы,
 - деформацияланбаған күйдегі тізбектің ұзыныдығы,
- деформацияланбаған күйдегі тізбектің ұзыныдығы,
 -оның деформациясына байланысты тізбектің үзілу мүмкіндігі.
-оның деформациясына байланысты тізбектің үзілу мүмкіндігі.
Егер де ұзындық бірлігі ретінде аморфтық қабаттың ұзындығын алатын болсақ, онда кристаллиттерден тізбек шығару нәтижесінің ескерілмеуінде
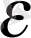 мөлшері
l
байланысты:
мөлшері
l
байланысты:
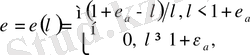 (1. 12)
(1. 12)
мұнда
 аморфтық қабаттың деформациясы болып табылады.
аморфтық қабаттың деформациясы болып табылады.
P( l, t) функциясы [7-9] келтірілген теңдеуге бағынады:
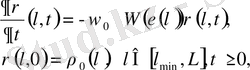 (1. 13)
(1. 13)
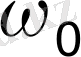 коэффициенті
W(
коэффициенті
W(
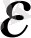 ) =1 мүмкіндігіне жауап беретін тізбектер үзілуінің жиілігімен дәлелденеді. [2] -де сияқты тізбек үзілісі бір жылулық тербеліс уақыты ішінде болады деп есептейік, ол [2] -ге сәйкес
) =1 мүмкіндігіне жауап беретін тізбектер үзілуінің жиілігімен дәлелденеді. [2] -де сияқты тізбек үзілісі бір жылулық тербеліс уақыты ішінде болады деп есептейік, ол [2] -ге сәйкес
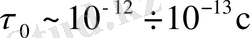 ,
,
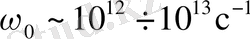 болып табылады.
болып табылады.
[10] -ға сәйкес, 4 түйнектерден тұратын қысқа учаскедегі тізбек үзілуінің мүмкіндігі былай суреттеледі:
 (1. 14)
(1. 14)
[10] -мен салыстырғанда біз
W(
 ) формуланы деформация терминдарында көшіріп жаздық.
) формуланы деформация терминдарында көшіріп жаздық.
Мұнда,
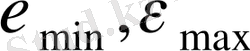 - молекула осінің бағытында химиялық байланыстың максималды және минималды деформациялары,
- молекула осінің бағытында химиялық байланыстың максималды және минималды деформациялары,
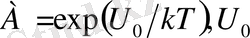 -үзілу активациясының энергиясы, Т - температура, k - Больцманның тұрақтысы,
-үзілу активациясының энергиясы, Т - температура, k - Больцманның тұрақтысы,
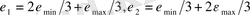
ε
=0 деформация тізбектің тепе-теңдік күйіне жауап береді, сондай-ақ (1. 13) формуласы бойынша есептелген оның үзілу мүмкіндігі нольге тең, ал
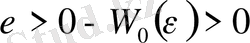 . Онда (1. 13)
ε
1
=0 қарай, мынаны шығаруға болады:
. Онда (1. 13)
ε
1
=0 қарай, мынаны шығаруға болады:
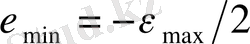 (1. 15)
(1. 15)
4-түйіндерден құрылған тізбек учаскесінің деформаланбаған ұзындығын
 арқылы белгілейік, онда
арқылы белгілейік, онда
 ұзындығы бар тізбекте
ұзындығы бар тізбекте
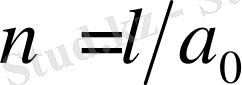 осындай учаскелері бар. Бойлы деформация тізбектің ұзындығы бойынша біркелкі орналасқан деп есептейік. Онда оның үзілу мүмкіндігі бар:
осындай учаскелері бар. Бойлы деформация тізбектің ұзындығы бойынша біркелкі орналасқан деп есептейік. Онда оның үзілу мүмкіндігі бар:
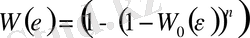 (1. 16)
(1. 16)
l min мөлшерін белгілейік.
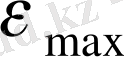 мөлшерінің мағынасы бойынша тізбектің минималды ұзындығы теңдікті қанағаттандырады:
мөлшерінің мағынасы бойынша тізбектің минималды ұзындығы теңдікті қанағаттандырады:

Осыдан және (1. 13) -ден
Equation. 3 екені шығады. Деформацияланбаған күйдегі тартылған тізбек жоқ деп есептей отырып, l min үшін формуланы нақтылайық:
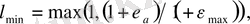 (1. 17)
(1. 17)
(1. 16) теңдеу (1. 13), (1, 14), (1. 15), (1. 17) бірге
 берілген деформалау заңы үшін аморфтық қабаттың деформалану және бұзылу процессін үлгілеуге мүмкіндік береді.
берілген деформалау заңы үшін аморфтық қабаттың деформалану және бұзылу процессін үлгілеуге мүмкіндік береді.
 байланысты жеке жағдайды қарастырайық.
байланысты жеке жағдайды қарастырайық.
Мұндай жағдайда (1. 16) жеңіл түрде ықпалдасады:
 (1. 18)
(1. 18)
Жоғарыда біз кристаллиттерден тізбекті шығару нәтижесін елемедік. Сонымен қатар, біз [14] -ке негізделеміз, ол релакциялық бұзылулар арнайы сипатталады.
ε
а
тұрақты деформациясы орнатылғанан кейін процесстің алдынғы тарихы бізге белгілі
t
= 0 кезіндегі тек қана
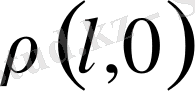 функцияда бейнеленеді деп есептейміз.
функцияда бейнеленеді деп есептейміз.
Бұзылу функциясын бұзылған тізбектер санының қатынасы арқылы олардың бастапқы санына шығарамыз:
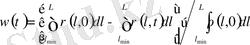 (1. 19)
(1. 19)
Тізбекті тарту күші деформациясына үйлесімді деп санайық. Онда көлденең қимада құрылған әрекет
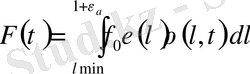 (1. 20)
(1. 20)
мұнда f 0 -материалдың константы ретінде қарастыратын күштің өлшемділік көлемі болып табылады.
F
(
t
) әрекеті әр
l
сайын
t
бойынша
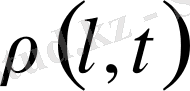 функциясының кемуіне сәйкес уақыт бойы төмендейді.
функциясының кемуіне сәйкес уақыт бойы төмендейді.
(1. 19) -(1. 20) формулалар аморфтық қабаттағы бәсеңдейтін күшті және бұзылу динамикасын есептеуге мүмкіндік береді.
Соңғы уақытта бірыңғай температура кезінде полимерлерді эксплуатациялау практикасында статикалық қажу құбылысы байқалды. Бұл құбылыс жан-жақты болып табылды, яғни барлық қатты полимерлерге тән. Осындай жағдайда, бұзылу температурамен тездетілетін материалдың ішкі бұзылуымен жиналған кинетикалық процесс болып табылады.
Статикалық қажу құбылысы беріктіктің сынды сипаты туралы ұғынымды қайта қарауға және материалдардың қысқамерзімді беріктігі туралы мәліметтердің практикалық маңыздылығын өзгеше бағалауға мәжбүрлейді, өйткені полимерлік материалдардың кернеу ұзақтылығы мен режиміне тәуелділігі айқын көрінеді.
Кинетикалық тұжырымға сәйкес бұзылу мен ұзақ беріктікті жиналудың кейбір жылдамдығымен және ұзақ мерзміділік сияқты ықпалды мөлшермен сипаттауға болады. Полимерлердің беріктік қасиеттерінің феноменологиялық зерттеулері ұзақ мерзімділіктің температуралық тәуелдлігініне немесе бұзылудың өсу жылдамдылығына ұшыратады.
Тұрақты созылу кернеу кезінде жылжымалылық процессінің барысында ұзақ беріктікті зерттеу кернеудің белгілі интервалында кинетиканың бұзылу процессі төменде Аррениустың теңдеуімен суреттелген кинетикалық процесстің кәдімгі тәуелділігіне жататынын көрсетті.
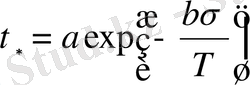 (1. 21)
(1. 21)
мұнда,
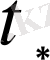 - тұрақты созылу кернеу салынған сәттен бастап бұзылу кезеңге дейін өткен уақыт; Т - абсолюттік температура;
а, b
- зерттелетін материалдың қасиеттерін сипаттайтын коэффициенттер.
- тұрақты созылу кернеу салынған сәттен бастап бұзылу кезеңге дейін өткен уақыт; Т - абсолюттік температура;
а, b
- зерттелетін материалдың қасиеттерін сипаттайтын коэффициенттер.
Мақталы бауды беріктіккке сынау кезінде бұзылғанға дейін уақыттың санды бағасын Буссе берді, ол 1971 жылы беріктіктің уақытша тәуелділігі экспонентамен аппроксималанатынын көрсетті
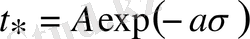 (1. 22)
(1. 22)
мұнда,
 - тұрақты созылатын кереу, А, a - материалдың параметрлері.
- тұрақты созылатын кереу, А, a - материалдың параметрлері.
Ұзақ мерзміділіктің температурадан тәуелділігін зерттеу қортындылары Бусқа статикалық бұзылулардың активациялық табиғаты бар деген болжамына негіздеме берді. Осының нәтижесінде жасанды жібек, мақта және нейлон үшін ұзақмерзімділіктің температуралық тәуелділігі теңдеуге бағынатыны табылды:
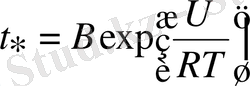 (1. 23)
(1. 23)
Мұнда, R - Больцманның тұрақтылығы, U - бұзылу активациясының әсерлі энергиясы, B - кернеуге байланысты экспоненциалды көбейткіш.
Ұзақ беріктіктің және қатты денелердің бұзылу процесстерінің, оның ішінде полимерлердің жүйелі зерттеуі С. Н. Журковпен және қызметкерлермен жүргізілген. Оның қортындысында эмпирикалық тәуелділік алынды:
 (1. 24)
(1. 24)
мұнда, t 0 - тұрақты, (10 -11 -10 -13 c) атомдардың жылу тербеліс кезеңдеріне санды тұрғыда жақын, R- Больцманның тұрақтысы;
Т - абсолютті температура, U
0
- активацияның энергиясы, өлшемі бойынша металлдар мен полимерлерге арналған химиялық байланыстардың энергия сублимациясының энергиясына жақын;
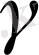 - құрылымды коэффициент.
- құрылымды коэффициент.
(1. 20) формулаға сәйкес тұрақты кернеу кезінде жарты логарифмикалық координаттарда кері температураның мөлшерінен бұзылуына дейін уақыттың тәуелділігі бір нүктеде жиналатын түзулердің сериясы болып табылады. Бірақ та, бұл формула кернеу жоқ болған кезде бұзылғанға дейін ақырғы уақыттың болуына және
 кезінде температурадан бұзылуына дейін уақыттың тәуелсіздігіне себеп болады. Сонымен, осы эмпирикалық формула кернеудің белгілі диапазонында ғана қолданылады және оның шеңберінен экстраполяциясы үшын жарамсыз, өйткені бұзылудың өте қысқа және өте ұзақ уақыттарында сараптау мәліметтердің шашылуы ерекше орын алады. Қортындылардың ең аз шашылуы ұзақ мерзімдіктің орташа мағыналарында байқалады, бұзылу уақытының осы диапазонында сараптау мәліметтер С. Н. Журковтың формуласымен келісіледі. Сонымен қатар, осы формула ұзақ беріктіктің термофлуктуациялық сипатын белгілейді.
кезінде температурадан бұзылуына дейін уақыттың тәуелсіздігіне себеп болады. Сонымен, осы эмпирикалық формула кернеудің белгілі диапазонында ғана қолданылады және оның шеңберінен экстраполяциясы үшын жарамсыз, өйткені бұзылудың өте қысқа және өте ұзақ уақыттарында сараптау мәліметтердің шашылуы ерекше орын алады. Қортындылардың ең аз шашылуы ұзақ мерзімдіктің орташа мағыналарында байқалады, бұзылу уақытының осы диапазонында сараптау мәліметтер С. Н. Журковтың формуласымен келісіледі. Сонымен қатар, осы формула ұзақ беріктіктің термофлуктуациялық сипатын белгілейді.
- Малекулалық қүрылым бойынша есеп
Молекулалық құрылымның параметрлерінің бірі -
 мөлшері, мұнда
L
a
- аморфтық қабаттың ұзындығы,
L
- үлкен кезеңнің ұзындығы [14]
.
мөлшері, мұнда
L
a
- аморфтық қабаттың ұзындығы,
L
- үлкен кезеңнің ұзындығы [14]
.
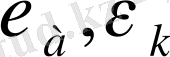 - аморфтық және кристалдық фазалардың орташа деформациясы, [16] -да көрсетілгендей
ε
м
макроскопикалық деформациясы үлкен кезеңнің деформациясына тең. Осыдан
- аморфтық және кристалдық фазалардың орташа деформациясы, [16] -да көрсетілгендей
ε
м
макроскопикалық деформациясы үлкен кезеңнің деформациясына тең. Осыдан
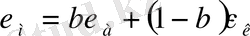 .
.
Сонымен,
ε
а
өлшемін макроскопикалық деформациясымен байланыстырғаннан кейін, (1. 19) -(1. 20) ара қатынастар бойынша тәуелділігінен бұзылу
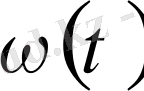 және бәсеңдейтін күш
F
(
t
) уақытынан тәуелділігін есептеуге болады.
және бәсеңдейтін күш
F
(
t
) уақытынан тәуелділігін есептеуге болады.
Егер де аморфтық қабат ұзындығының тегіс еместігін елемесек, онда (1. 20) теңдеуі үлгідегі көлемде
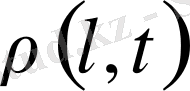 тізбектердің ұзындығы бойынша таралуды белгілейді. Сонымен қатар,
тізбектердің ұзындығы бойынша таралуды белгілейді. Сонымен қатар,
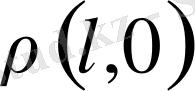 функциясының аморфтық қабаттардың барлық жиынтығында тізбектердің бастапқы бөлу мағынасы бар.
функциясының аморфтық қабаттардың барлық жиынтығында тізбектердің бастапқы бөлу мағынасы бар.
[13] қорытындыларында негізделе отырып, субмикротрещиналардың сын концентрациясына жауап беретін ω кр бұзылудың мағынасы бар деп есептейік.
Сонда, ω ( t ) = ω кр теңдеу ашық емес түрде кернеудің бәсеңдеуі кезінде үлгінің ұзақ мерзімдігін белгілейді.
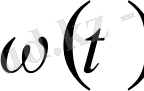 үшін формуланы талдай отырып, ұзақ мерзімдік макроскопикалық деформацияға
үшін формуланы талдай отырып, ұзақ мерзімдік макроскопикалық деформацияға
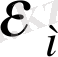 ,
β
молекулалық құрылымның параметріне, аморфтық қабаттың ұзындығына, Т температураға,
,
β
молекулалық құрылымның параметріне, аморфтық қабаттың ұзындығына, Т температураға,
 бөлуіне байланысты
.
бөлуіне байланысты
.
Релаксация қисық негізінде есеп .
Полимерлер механикасында практикалық есептерде сараптау түрде шығатын қисық жылжулар негізінде қисық релаксация құру әдістемесі бар. (1. 12) -(1. 4) тапсырманы шешу үшін осы әдіс қолданылған. Осы үшін теңдеулердің жай ықпалдасуымен шығатын қисық релаксациялардың жиынтығы құрылған болатын (1. 13) .
Осылар арқылы изохронды қисықтардың жиынтығы құрылады. Изохронды қисықтар мен қисық бәсеңдеу негізінде қисық жылжымалылықтар құрылады .
(1. 12/-(1. 14) тапсырма шешуінің итерационды әдісінің схемасы .
q(t) =1+ ε а (t ) арқылы белгілейік, сонда q(t) үшін (1. 12) теңдеу мынадай түрде жазылады:
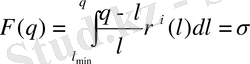 (1. 25)
(1. 25)
1. ∆t, t i =i ∆t уақыт бойынша қадам белгілейік.
ρ i (l) = ρ(l, t i . ), q i =q(t i ), ρ 0 (l) = ρ(l, 0. ), q 0 =1 + ε 0 белгілейік, i>0 үшін итерация орындаймыз:
2. ρ i (l) берілгенмен (1. 13) қанағаттанатын q i табу қажет, ол үшін q арнайы (1. 25) теңдеуді шешу қажет.
3. (1. 14) -ден q =q i берілгенмен ρ i+1 (l) табу керек.
4. с i=i+1 2 қадамына қайта оралу.
Әр итерация кезінде бұзылудың мағынасын бақылаймыз.
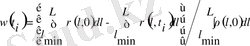 (1. 26)
(1. 26)
Ұқсастықты тексеру үшін уақыт бойынша есеп жүргізіп, қорытындыларды салыстыру қажет.
Есеп айырылысу бағдарламасының қисынды модульдары:
1. Барлық физикалық параметрлерді белгілеу.
2. Ықпалдасу нүктелер санының есеп айырылысу параметрлерін, уақыттың ақырғы кезеңін белгілеу.
3. ρ 0 (l) = ρ(l, 0. ), q 0 =1 + ε 0 функцияларының бастапқы мәнін осылай ала отырып, σ - ді есептеу.
4. (5) теңдеуді шешуге арналған бағдарламаша.
5. q i -ді есептеу
- ρi(l) есептеу
- Келесі итерацияға 5, 6 қайталау.
- Бұзулықты есептеу. Сын мағына асқаннан кейін итерацияны тоқтату.
- Есеп айырылысуды аяқтауға берілген уақытқа жеткеннен кейін, итерацияны тоқтату.
- 30% дейін уақытты есептеу.
11. бұзылулар
12. Мәліметтердің қортындысы.
- Есептеулер нәтижесі
Релаксация құбылысы үшін ұзақ өмірліктің есептері бойынша қорытындылар келтірейік (1. 12) .
[10] -да
 (
t )
есеп тәуелділігіне сүйене отырып, 10
(
t )
есеп тәуелділігіне сүйене отырып, 10
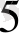 с бірліктерде үлгінің ұзақ мерзімділігі белгіленді. Сын бұзылудың көлемі 0, 3 тең қабылданған болатын, сонда осы мағынаға жауап беретін уақыт кезеңі ұзақ мерзімдікті көрсетеді.
с бірліктерде үлгінің ұзақ мерзімділігі белгіленді. Сын бұзылудың көлемі 0, 3 тең қабылданған болатын, сонда осы мағынаға жауап беретін уақыт кезеңі ұзақ мерзімдікті көрсетеді.
Есептерде β = 0, 5, ал бұзылуға дейінгі уақыт әр түрлі температура мен деформациялар үшін белгіленеді.
ω
0
мағынасы полиэтилен үшін бағамен келісілген және де
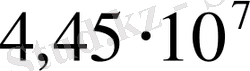 с
-1
тең берілген.
с
-1
тең берілген.
Бірқатар параметрлер мағынасының белгісіздігіне қарамастан, есептеу қорытындылары теориялық ұзақ мерзмідіктің эксперименттермен қанағаттанарлы келісуін көрсетеді [14] . Температура көтерілу және деформация ұлғаю кезеңіндегі экспериментпен салыстырғанда қаралып отырған модель бойынша есептелген ұзақмерзімдіктің мағынасының төмендеуі назар аудартады.
Мүмкін, бұл жоғары температура кезінде полимердің аморфизация деңгейі өсіп, кристаллиттерден тізбек шығару арқылы ρ ( l , 0) функциясында елеулі өзгерістер болатынымен түсіндірілетін шығар. Бұдан басқа, біз деформация өсу кезінде тізбектердің қосымша бағытын ескермедік.
2. Крип құбылысының термофлуктуациялық мо делін жасау
2. 1 Амофты қабаттағы крип құбылысының моделін жасау
[5] жұмысында [4] -ші жұмыстың нәтижесін қолдана отырып, аморфты қабатша бұзылуының математикалық модельі алынған. Осының нәтижесінде аморфты-кристаллды полимерлердің бұзылу динамикасы, релаксация күші, кернеу релаксациясы жағдайындағы төзімділігі есептелген. Модельдің негізгі параметлері етіліп тасымалдаушы шынжырлардың максимальді және минимальді деформациялары, үзілудің активациялық энергиясы, шынжырлар ұзындығы бойынша таралу функциясы, температура микраскопиялық деформация, аморфты қабаттың қатынасты өлшемдері алынған. Феноменологиялық теория модельі мен материалдың релаксация спектрінің ішкі молекулярлық, құрылыстық сипаттамасы арасында және модельдің параметрлерін іріктеу негізінде полиэтилен беріктігінің эксперименттік зерттеу бойынша алынған қорытындыларымен қабылдауға болатын сәйкестік алынды.
Бұл жұмыста [5] жұмысы негізінде бірөсті созу жағдайындағы криптің термофлуктуациялық механизмінің математикалық моделі жасалады.
Алынған материалдың құрылысы [5, 7-10] жұмыстардағыдай аморфты-кристалды деп қарастырайық. Мұндағы тасушы элементтер ұштары кристалиттерге бекітілген әртүрлі ұзындықтардағы шынжырлар және деформация аморфты қабаттардың негізінде іске ассын.
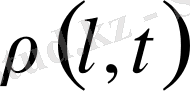 - t уақыттағы аморфты қабатшадағы тасушы шынжырлардың ұзындығы бойынша таралу тығыздығы (
l
-шынжырдың деформацияланбаған күйдегі ұзындығы),
- t уақыттағы аморфты қабатшадағы тасушы шынжырлардың ұзындығы бойынша таралу тығыздығы (
l
-шынжырдың деформацияланбаған күйдегі ұзындығы),
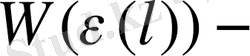 ұзындығы
ұзындығы
 шынжырдың оның деформациясына тәуелді үзілу ықтималдығы.
шынжырдың оның деформациясына тәуелді үзілу ықтималдығы.
 функциясы төмендегі теңдеуге тәуелді:
функциясы төмендегі теңдеуге тәуелді:
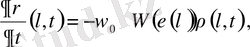 (2. 1)
(2. 1)
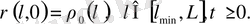 (2. 2)
(2. 2)
Осындай теңдеулер [7-9] -жұмыстарында қарастырылған.
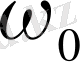 коэффициенті ([1] )
коэффициенті ([1] )
 ықтималдыққа жауап беретін шынжырлардың мүмкін үзілу жиілігін көрсетеді.
ықтималдыққа жауап беретін шынжырлардың мүмкін үзілу жиілігін көрсетеді.
 -бойлық деформациясы шынжырлардың ұзындығына бірқалыпты таралған деп қарастырайық. Онда оның үзілу мүмкіндігі:
-бойлық деформациясы шынжырлардың ұзындығына бірқалыпты таралған деп қарастырайық. Онда оның үзілу мүмкіндігі:
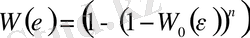 (2. 3)
(2. 3)
Мұндағы
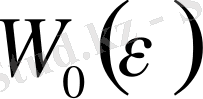 - бір элементар аймақтың үзілу ықтималдығы, ал n- осындай аймақтардың саны.
- бір элементар аймақтың үзілу ықтималдығы, ал n- осындай аймақтардың саны.
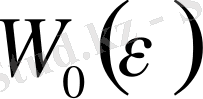 -ге арналған формулада үш көршілес байланыстың тасушы шынжырлардың үзілуіне әкеліп соқтыруы мумкін біріккен жылу флуктуациясы ескеріледі. [4] жұмысында өзіміз қорытып шығарған және [5] жұмысында қолданылған
-ге арналған формулада үш көршілес байланыстың тасушы шынжырлардың үзілуіне әкеліп соқтыруы мумкін біріккен жылу флуктуациясы ескеріледі. [4] жұмысында өзіміз қорытып шығарған және [5] жұмысында қолданылған
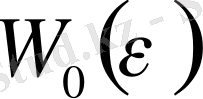 үшін жазылған өрнек мына түрдежазылған:
үшін жазылған өрнек мына түрдежазылған:
 (2. 4)
(2. 4)
Мұнда,
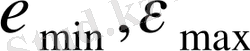 - молекула осінің бағытында химиялық байланыстың максималды және минималды деформациялары,
- молекула осінің бағытында химиялық байланыстың максималды және минималды деформациялары,
 -үзілу активациясының энергиясы, Т - температура, k - Больцманның тұрақтысы,
-үзілу активациясының энергиясы, Т - температура, k - Больцманның тұрақтысы,
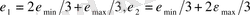
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz