Полиномдық сплайндар мен жуықтау теоремелері: интегралдық теңдеулерді жуықтап шешу және қатенің бағалануы


Мазмұны
Кіріспе . . . 3
§1 Сплайн функциялар. Оларды бейнелеудің негізгі үлгілері . . . 5
§2 Жуықтау теоремалары . . . 9
§3 Интегралдық теңдеулерді сплайындар көмегімен жуықтап шешу…… . . . 13
Қорытынды . . . . . . 20
Пайдаланылған әдебиеттер . . . . . 21
Кіріспе
Қазіргі кездегі математикалық зерттеулерде әсіресе оның қолданбалы бағыттарында жуықтау теориясының нәтижелері мен тәсілдері кеңінен қолданылуда. Жуықтау теориясының қарқанды дамып келе жатқан бағытының бірі - сплайндар теориясы.
Қазіргі кезде сплайндар ұғымына әр түрлі пайым бар болғанымен, классикалық үрдіс сплайндар осы бөлікті полиномдық функцияларды пайымдайды.
Сплайн функцияларының жуықтау теориясындағы бұрыннан кеңінен қолданыста болып келген әрі әлі өз маңызын жоғалтпаған классикалық алгебраның көпмүшеліктерден ерекшелейтін, олардан оздырып алдыңғы қатарға алып шыққан көптеген жақсы қасиеттері бар. Солардың маңыздыларының бірнешеуін көрсете кетсек, сплайндар жуықтау құралы ретінде көпмүшеліктерден гөрі жуықталып жатқан функция табиғатын өте қолайлы екен, әсіресе бұл көрініс тегістік көрсеткіші арқылы болатын функцияларды жуықтағанда көзге түседі. Қолданбалы салаларда, соның ішінде есептеу математикасында сплайндарға қызығушылық оның локальдылық қасиеттерімен және үлкен дәлдікке көпмүшелік дәрежесін көп өсірмей-ақ қол жеткізу мүмкіндігін түсіндіруге болады. Оның үстіне сеткалық түрде берілген функцияны интерполяциялық сплайн аралықта барлық нүктелерінде қалпына келтіреді.
Ал таза теориялық негізін жуықтау теориясында сараптасақ көп жағдайда классикалық функциялық кластарда өлшемдері бірдей ішкі кеңістіктер арасында сплайндар кеңістігі минималды ауытқуды жүзеге асырады. Оның үстіне түйіндестік теоремалары жуықтау теориясының кейбір экстремалды мәселелерінің шешімі ретінде тағы да сплайндар пайда болатынын көрсетеді.
Бұл жұмыста, негізінен, сплайндар мәселенің классикалық қойылымында анықталып үзіліссіз және тегіс функцияларды жуықтау мүмкіндіктері қарастырылған.
Бұл теоремалардың қолданысы ретінде, және дипломдық жұмыстың негізгі нәтижесі ретінде аталған теоремаларға сүйене отырып, интегралдық теңдеулерді және шекаралық мәселелерді жуықтап шешудің бір жолы ретінде сплайн-функцияларды қолдану мүмкіндігі зерттелген. Бұндай шешімнің бар болатыны дәлелденіп, оның дәл шешімінен ауытқуы бағаланған. Бұл бағалаулар аралықты бөліктеу диаметрі мен функцияның немесе оның туындылырының үзіліссіздік модульдері терминдерінде алынған.
§1 Сплайн функциялар. Оларды бейнелеудің негізгі үлгілері
Анықтама 1: S m (x) =S m, k (x, ∆ n ) функциясы
∆ n : a = x 0 < x 1 < … < x n < x n+1 = в (1)
түйідерінде ақауы k 1 ≤ k ≤ m дәрежесі m-нен аспайтын полиномдық сплайн деп аталады.
1) S m (x) ∈ Р m [x і , x і+1 ] (і = 0, 1, 2, … n) ;
2) S m (x) ∈ C m-k [a, b]
{x і } нүктелері сплайн түйіндері деп аталады.
[a, b] сегментінде S m (x) (m-k+1) -ші туындысы үзілісті болып табылады.
Көп жағдайда біз дефекті 1-ге тең полиномдық сплайндарды қарастырамыз.
Осы сияқты үш жағдай қарастырамыз
m ∈ N, (x-t) m = [max(0, x-t) ] m
қалдық мүшелі Тейлор формуласын интегралдық түрде өрнектеуге болады.
f(x) =
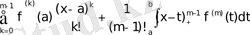 (2)
(2)
а ≤ х ≤ в
Егер f(x) = C m [a, b], онда (2) пайдаланып, дәрежесі n ≥ m-1 болатын Лагранж интерполяциялық көпмүшелігінің қалдық мүшесін төмендегідей жазуға болады:
f(x) =
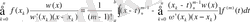 (3)
(3)
мұндағы x k - интерполяция түйіндері және
ω(х) = (x-x 0 ) (x-x 1 ) … (x-x n )
f (x
k
, x
k+1
) =
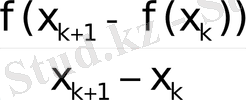 Equation. 3 және
Equation. 3 және
f (x
k
, …, x
k+m
) =
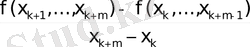 Equation. 3
Equation. 3
(m≥1) болсын,
мұндағы х і - (1. 1) түрінде беріледі. f (x k , …. , x k+m ) шамасы m дәрежелі f(x) функциясының бөліктелген айырмасы деп аталады.
f(x
k
, …., x
k+m
) =
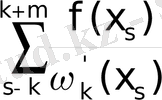 Equation. 3 (4)
Equation. 3 (4)
мұндағы ω k (х) = (x-x k ) =(x-x k ) (x-x k+1 ) …. . (x-x k+m )
Егер f(x) ∈ C m [a, b], m∈N, онда (2) -ні ескерсек m ретті бөліктелген айырым көпмүшелігінің төменгі дәрежесі нөлге тең. Одан
f(x
k
, …. . , x
k+m
) =
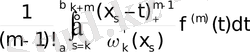 Equation. 3 (5)
Equation. 3 (5)
(0 ≤ k ≤ k+m ≤ n) аламыз.
(2), (3) және (5) түрлендірулеріндегі ядролар - Пеано ядролары деп аталады. Сондай-ақ олар айналмалы ақауы 1-ге тең m-1 дәрежелі сплайндер болып табылады. Мұнда (2) - түрлендірудің жалғыз х түйіні бар. Ал х, х 0 х 1 , …, х n нүктелері (3) интегралдық түрлендіруіндегі сплайн түйіндері болса, x k , x k+1 , … x k+m нүктелері (5) -гі түйіндер
Белгілеу енгіземіз
B
m-1
(t) = B
m-1
(x
k
, x
k+1
, … x
k+m
t) = m
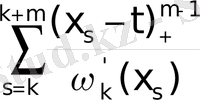 Equation. 3 (6)
Equation. 3 (6)
(x k < x k+1 < … < x k+m ) .
B m-1 (t) функциясын түйіндері x k , x k+1 , …, x k+m болатын дәрежелі B сплайн деп атаймыз. Жеке жағдайларда В сплайндарды анықтай тын базистік функция ретінде қарастырған ыңғайлы.
Анықтама2. S 2 (x; f) функциясы f(x) функциясы үшін интерполяциялық параболалық сплайн деп аталады.
Егер
1) S
2
(x) ∈ Р
2
, х ∈ (
 Equation. 3,
Equation. 3,
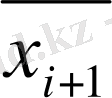 Equation. 3 ) (і = 0, 1, 2, … n) ;
Equation. 3 ) (і = 0, 1, 2, … n) ;
2) S 2 (x) ∈ C (1) [a, b] ;
3) S 2 (x і ) = f(x і ) , (і =0, 1, 2, … n)
орындалса
 - сплайн түйіндері,
- сплайн түйіндері,
x і - интерполяция түйіндері.
S 2 (x) сплайны n+3 парметрден тәуелді, демек 2 бос параметрі бар. Сондықтан интерполяциялық параболалық сплайнына екі қосымша шарт қойылады.
Егер f(x) функциясы (b-а) периодты болса, онда S (x) сплайны да (b-а) периодты болады. Оның (
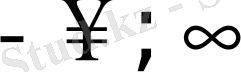 ) аралағында бірінші ретті үзіліссіз туындысы бар. S (x) периодты сплайны мына шартты қанағаттандырады:
) аралағында бірінші ретті үзіліссіз туындысы бар. S (x) периодты сплайны мына шартты қанағаттандырады:
α)
 (і =1, 2) (7)
(і =1, 2) (7)
Жалпы жағдайда келесі шекаралық шарттар қолданылады:
β)
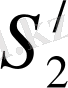
 ,
,
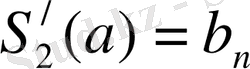
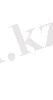 (8)
(8)
γ)
 ,
,
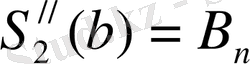 (9)
(9)
мұндағы а n , b n , А n , В n ∈R. Бұл сандарды дәл таңдау, қарастырылып отырған есептен тәуелді. Мысалы, егер f(x) функциясының сәйкесінше туындылары
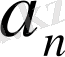 =
=
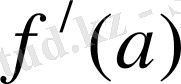
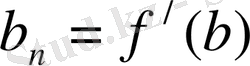 ,
,
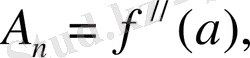
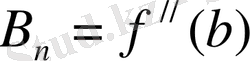 болса, оларды жуық мәндерінің сәйкес туындыларымен ауыстыруға болады.
болса, оларды жуық мәндерінің сәйкес туындыларымен ауыстыруға болады.
Бұл мына шартқа эквивалентті:
δ)
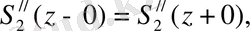 z=
z=
 , (і =1, n) (10)
, (і =1, n) (10)
m
і
=
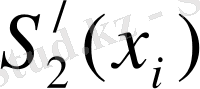 , (і =0, 1, …, n) (11)
, (і =0, 1, …, n) (11)
M
і
=
 , (і =0, 1, …, n) (12)
, (і =0, 1, …, n) (12)
Сондай-ақ
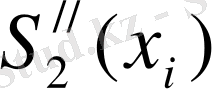 - бөлік тұрақты функция, онда
- бөлік тұрақты функция, онда
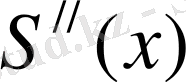 = M
і
,
= M
і
,
 ≤ x< x
і+1
(і =0, 1, …, n) (13)
≤ x< x
і+1
(і =0, 1, …, n) (13)
h і = x і+1 - x і (і =0, 1, …, n-1),
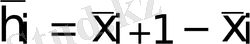 (і =0, 1, …, n-1) .
(і =0, 1, …, n-1) .
болсын.
Мұндағы f (x к-1 , х к , х к+1 ), x к-1 , х к , х к+1 нүктелеріне қатысты f(x) функциясының екінші бөліктелген айырымы.
Анықтама 3. S 3 (f) =S 3 (x; f) функциясы f(x) функциясы үшін нтерполяциялық кубтық сплайн деп аталады.
Егер
- S3(x; f) ∈ Р3, х ∈ (xі, xі+1), (і = 0, 1, 2, … n-1) ;
2) S 3 (x; f) ∈ C (2) [a, b] ;
3) S 3 (x і ; f) = f(x і ) , (і =0, 1, 2, … n) , n ≥ 2
1 анықтаманың сонғы жағында айтылғандай кубтық сплайндардың екі бос параметрлері бар. Әдетте интерполяциясылық сплайндарға қосымша шекаралық шарттар қойылады. Біз параболалық сплайндар үшін қойылған шекаралық шарттармен шектелеміз:
α)
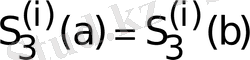 (і =1, 2) (14)
(і =1, 2) (14)
β)
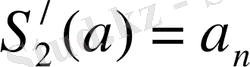 ,
,
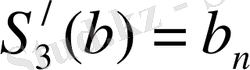 (15)
(15)
γ)
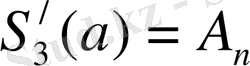 ,
,
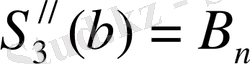 (16)
(16)
δ)
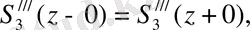 z= x
1
, x
n-1
(17) .
z= x
1
, x
n-1
(17) .
§ 2. Жуықтау теоремалары.
Теорема 1
. Егер f(x) ∈
 Equation. 3 немесе f(x) ∈ С
(2)
[ a, b], онда
Equation. 3 немесе f(x) ∈ С
(2)
[ a, b], онда
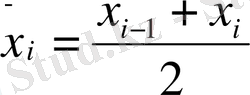 Equation. 3 (і = 0, 1, 2, …, n) ; түйіндерінде (f∈
Equation. 3 (і = 0, 1, 2, …, n) ; түйіндерінде (f∈
 Equation. 3 болғанда) периодты шекаралық шарттарды немесе ( f(x) ∈ С
(2)
[ a, b] болғанда)
Equation. 3 болғанда) периодты шекаралық шарттарды немесе ( f(x) ∈ С
(2)
[ a, b] болғанда)
1) х (t) -Р n *(t) С[a, b ] = mіn х (t) -Р n (t) С[a, b] (1)
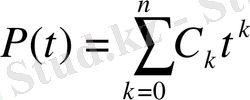
ω (х, δ) функциясы δ бойынша келеімейтын функция.
ω (х, δ 1 +δ 2 ) ≤ ω (х, δ 1 ) + ω (х, δ 2 )
ω (х, nδ) ≤ n ω(х, δ) , (n∈N) (2)
ω (х, λδ) ≤ ([λ] +1) ω(х, δ) , (λ∈R + )
[λ] - λ-ң бүтін бөлігі
шекаралық шарттарын қанағаттандыратын интерполяциялық параболалық слайны мына теңсіздікте орын алады:
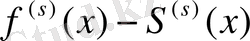 Equation. 3 ≤ К
S
∆
n
2-S
α
n
(3)
Equation. 3 ≤ К
S
∆
n
2-S
α
n
(3)
x∈[a, b] (S= 0, 1, 2),
периодты шекаралық шарттар және (2) шарттар үшін
α n = ω ( f′′, ∆ n ), (4)
(1) шекаралық шарты үшін
α n =3/7ω( f′′, ∆ n ) +max{4/7ω ( f′′, ∆ n , 8/7 [ f(x 0 , x 1 ) -а n ] ƒh 0 -1 -1/2 f′′(х 0 ) , 8/7 [ f(x n-1 , x n ) - b n ] ƒh -1 n-1 +1/2 f′′(x n ) }, (5)
Ал
х (t) ∈ С[ a, b] , ω (х, δ) = max х (t+h) - х (t)
t, t+h∈[a, b] (6)
0≤δ≤b-а
шарты үшін
α n = ω ( f′′, ∆ n ) +2/7max( f′′(x 0 ) -А n , f′′(x n ) -В n (7)
және
K 0 =7/8, K 1 = K 2 =7/2 (8)
Теорема 2.
Егер f(x) ∈С[ a, b],
 = h
і
/2 (і = 0, 1, …, k
n-1
)
= h
і
/2 (і = 0, 1, …, k
n-1
)
және
∆
n
: а =
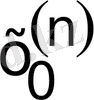 <
<
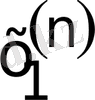 < … <
< … <
 = b
= b
түйіндерінде S 2 (x) интерполяциялық параболалық сплайны периодты шекаралық шарттарды (егер f(x) - (b-а) периодты болса) немесе (1) -(2) шекаралық шарттарды қанағаттандырса, онда келесі бағалау дұрыс
f(x) - S 2 (x) ≤ ω(f, ∆ n ) +2L n ∆ n +α n (9) периодты шекаралық шарттар және (2) шарты үшін α n = 0,
- шекаралық шарты үшін
α
n
= max(
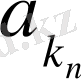 ,
,
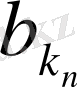 ) ∆
n
,
) ∆
n
,
- шекаралық шарты үшін
α
n
= max(
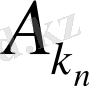 ,
,
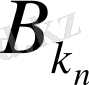 ) ∆
n
2
.
) ∆
n
2
.
Теорема 3.
Егер f(x) ∈ С
(S)
[a, b], S=0, 1, 2, онда S(х) интерполяциялық параболалық сплайны периодты шекаралық шарттарда (f∈
 ) немесе (1) -(2) шарттарында
) немесе (1) -(2) шарттарында
S(х) ≤ (1+4β) f і +α 0 , n
S′(х) ≤ (4+4β) f і ∆ n -1 +α 0 , n ∆ n -1 (10)
S′′ (х) ≤ (8+16β) f і ∆ n -2 +4α 0 , n ∆ n -2
( а ≤ х ≤ b )
S (S) (х) ≤ 2 f (S) +α S , n , S =1, 2, х ∈ [ a, b] (11)
теңсіздіктерін қанағаттандырады.
(10) жағдайында R(∆ n ) ≤ β теңсіздігі орындалады деп қосымша ұйғару жасаймыз;
(11) интерполяция түйіндерінде шегі жоқ және периотды шекаралық шарты және (2) шартында
α S , n = 0, S=0, 1, 2,
(1) шартында
α 0 , n = α 1 , n ∆ n , α 1 , n = max( а кn , b кn ),
α
2
,
n
= max( 0, 2
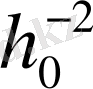 f(x
і
) - f(x
0
) а
n
f(x
і
) - f(x
0
) а
n
 - f′′
С[ a, b]
, (12)
- f′′
С[ a, b]
, (12)
2
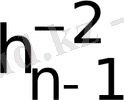 f(x
n
) - f(x
n-1
) b
n
f(x
n
) - f(x
n-1
) b
n
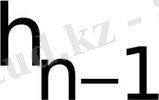 - f′′
С[ a, b ]
- f′′
С[ a, b ]
(6) шартында
α 0 , n = α 2 , n ∆ n 2 , α 1 , n =α 2 , n ∆ n ,
α 2 , n = max ( А n , В n ) (13) .
Теорема 4.
Егер f(x) ∈С
(2)
[a, b], f(x) ∈
 және ∆
n
: а = х
0
< х
1
< …< х
n
= b, (n≥2) сеткасына қатысты S
3
(x; f) интегралдық қубтық сплайны (15) -(17) шекаралық шарттарды (периодты шекаралық шарттарды) қанағаттандырын, келесі теңсіздікте орын алады.
және ∆
n
: а = х
0
< х
1
< …< х
n
= b, (n≥2) сеткасына қатысты S
3
(x; f) интегралдық қубтық сплайны (15) -(17) шекаралық шарттарды (периодты шекаралық шарттарды) қанағаттандырын, келесі теңсіздікте орын алады.
f (S) (x) - S 3 (S) (x; f) ≤ K S ∆ n 2-S α n ,
x∈[a, b] (S=0, 1, 2) (14)
мұндағы
K 2 = K 1 = 4K 0 =5
және периодты шекаралық шарттар үшін
α n =ω(f, Δ n ) (15) 15 шекаралық шарттар үшін (16)
ω( f′′, ∆ n ), а+ h 0 ≤ х ≤ b-h n-1 ,
ω( f′′, ∆
n
) max(
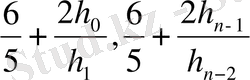 ),
),
х 0 ≤ х ≤ х 1 , х n-1 ≤ х ≤ х n
(13) шекаралық шарттар үшін
α
n
=
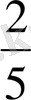 ω( f′′, ∆
n
) + max{
ω( f′′, ∆
n
) + max{
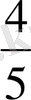 ω( f′′, ∆
n
),
ω( f′′, ∆
n
),
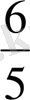 f(х
0
, х
1
) -
f(х
0
, х
1
) -
- а
n
-
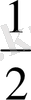 f′′(х
0
) ,
f′′(х
0
) ,
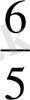 f(х
n-1
, х
n
) - b
n
+
f(х
n-1
, х
n
) - b
n
+
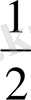 f′′(х
n
) } (17)
f′′(х
n
) } (17)
(14) шекаралық шарттар үшін
α
n
= ω(f′′, ∆
n
) +
 max {f′′(х
0
) -А
n
, f′′(х) -В
n
} (18)
max {f′′(х
0
) -А
n
, f′′(х) -В
n
} (18)
Теорема 5. Егер f(x) ∈С (3) [a, b], және S 3 (x; f) сплайны x і =а+іh, (і=0, 1, …, n) түйіндерінде f(x) функциясын түйіндерінде интерполяцияласа және (15) шекаралық шартты қанағаттандырса, онда
f (S) (x) - S 3 (S) (x; f) ≤ K S ∆ n 3-S ω(f′′, h) (19)
мұнда
S=0, 1, 2, 3 және K 3 =9, K 2 = 18, K 1 = 9, K 0 =9/2
Теорема 6. Егер f(x) ∈С (к) [a, b], Егер f(x) ∈С (2) [a, b], к= 0, 1, 2, 3 онда x і =а+іh,
h=(b-а) /n, n∈N бірқалыпты түйіндерінде интерполяциялық қубтық сплайны периодты шекаралық шарттарды немесе (15) шекаралық шарттарды қанағаттандырады.
S 3 (к) (x; f) ≤ 5 f (к) (x) (20) .
§3. Интегралдық теңдеулерді сплайндар көмегімен жуықтар шешу.
Фредгольмның ІІ-ретті интегралдық тендеуінің сандық шешімдеріүшін сплайндардың қолданылу мүмкіндіктерін қарастырамыз:
у(х) = f(x) + λ
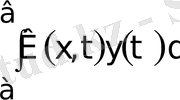 Equation. 3 (1)
Equation. 3 (1)
мұндағы
f(x) ∈C[a, b] К(х, t) ∈C(
 Equation. 3 ), (
Equation. 3 ), (
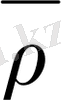 Equation. 3 ) =[a, b] × [a, b],
Equation. 3 ) =[a, b] × [a, b],
λ-нақты параметр . Біз түйіндері бірқалыпты болатын, сәйкесінше(1. 10 ) және
(1. 17) шарттарын қанағаттандыратын, қубтық және параболалық сплайндарды қарастырумен шектелеміз. n∈N, h=(b-а) /n және x і =а+іh, і= -1, 0, 1, …, n, n+1 болсын.
Түрлендірулерді қубтық сплайндар үшін қарастырамыз
S
3
(x) =
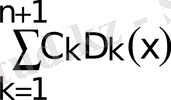 Equation. 3 (2)
Equation. 3 (2)
мұндағы
D
0
(х+а) =
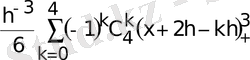 Equation. 3 (3)
Equation. 3 (3)
D 0 (х+а) = D 0 (х+а-kh)
Онда ( 1. 10 ) шекаралық шарты С k атауында мына түрде жазылады
С -1 = 4 С 0 - 6С 4 +4С 2 - С 3
С n+1 = 4 С n - 6С n-1 +4С n-2 - С n-3 (4)
Сол іспеттес параболалық сплайндар үшін де қолданамыз
S
2
(x) =
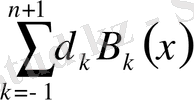 Equation. 3 (5)
Equation. 3 (5)
мұндағы
В
0
(х+а) =
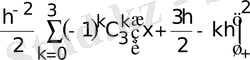 Equation. 3 (6)
Equation. 3 (6)
В k (х+а) = В 0 (х+а-kh)
Бұл жағдайда ( 1. 17 ) шекаралық шарты
d -1 =3d 0 - 3d 1 + d 2 , d n+1 = 3d n - 3d n-1 + d n-2 (7)
арақатысына эквивалентті.
Бастапқы шарттан S k (x), k=2, 3 сплайнын қарастырамыз.
S
k
(x
і
) = f(x
і
) + λ
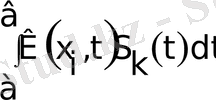 , (і=0, 1, …, n) (8)
, (і=0, 1, …, n) (8)
Басқаша k=3 болғанда (4) шарты, k=2 болғанда (7) шарты орындалады деп жорамалдаймыз. Олай болса келесі қорытынды дұрыс.
Теорема:
Егер λ
 Equation. 3
Equation. 3
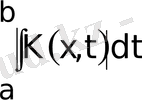 =ρ<1, а ≤ х ≤ в және (1) есептің у(х)
=ρ<1, а ≤ х ≤ в және (1) есептің у(х)
шешімі С (Р) [a, b] байланысты, онда (8) жүйе жалғыз шешім қабылдайды және
у
(і)
(x) - S
2
(і)
(x)
С[a, b]
≤
 Equation. 3 (9)
Equation. 3 (9)
(0≤ і ≤ р ≤ 2),
у
(і)
(x) - S
3
(і)
(x)
С[a, b]
≤
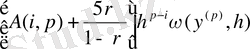 Equation. 3 (10)
Equation. 3 (10)
(0≤ і ≤ р ≤ 3),
мұндағы
В(0, 2) =
 Equation. 3, В(1, 2) = В(2, 2) =
Equation. 3, В(1, 2) = В(2, 2) =
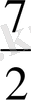 Equation. 3
Equation. 3
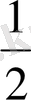 Equation. 3 В(1, 1) = В(0, 1) =
Equation. 3 В(1, 1) = В(0, 1) =
 Equation. 3, В(0, 0) = 2,
Equation. 3, В(0, 0) = 2,
А(і, 3) ≤ 18, А(і, 2) ≤ 16, А(і, 1) ≤ 17, А(0, 0) ≤ 9
Дәлелдеу: S k (x; у), k=2, 3 сплайны S k (x і , у) = у(x і ), і= 0, 1, …, n шартын қанағаттандыратын (2) немесе(5) түріндегі сплайнды білдіреді және сәйкесінше (7) немесе (4) шеқаралық шартын қанағаттандырса, онда
S
k
(x
і
, у) = f(x
і
) + λ
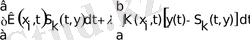 Equation. 3, (11)
Equation. 3, (11)
ϕ(х) = S k (x; у) - S k (x)
ϕ і =ϕ(х і )
ϕ
і
=
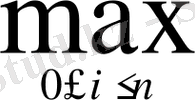 Equation. 3 ϕ
і
, (12)
Equation. 3 ϕ
і
, (12)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz