Қуыс ортадағы газдың бейстационарлық қозғалысы және серпімді сұйықпен ұқсастығы


ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Қ. И. Сәтпаев атындағы Қазақ Ұлттық Техникалық Университеті
Мұнай және газ кен орындарын игеру және пайдалану кафедрасы
Курстық жұмыс
Тақырыбы: ҚУЫСТЫ ОРТАДА ГАЗДЫҢ БЕЛГІЛЕНБЕГЕН ҚОЗҒАЛЫСЫ
Нормалық бақылау Тексерген: Абайолданова К. Ж.
Орындаған: Жеңісхан А.
Мамандығы: 200140
Тобы: ГН-03-2қ
АЛМАТЫ 2006
МАЗМҰНЫ
КІРІСПЕ4
2. ҚУЫСТЫ ОРТАДА ГАЗДЫҢ БЕЛГІЛЕНБЕГЕН ҚОЗҒАЛЫСЫ5
2. 1 Дифференциалдық теңдеуді сызықтау (линеаризация) . 5
2. 2. Серпімді сұйық газдың фильтрациясы арасындағы ұқсастық. 7
3. ЕСЕПТІҢ ШЫҒАРЫЛУЫ12
4. ҚОСЫМША17
ҚОРЫТЫНДЫ18
ӘДЕБИЕТТЕР TI3IMІ19
КІРІСПЕ
Серпімді қуысты ортада серпімді сұйық пен газдың белгіленбеген фильтрациясымен әр түрлі шекті есептерін шешуге жеке туындылардағы сызықты дифференциал тендеулері жақсы белгілі, интегралдау әдісінің көмегімен жетуге болады. Көптеген жағдайда бұл шешімдер өте үлкен болып келеді.
Қысқарту үшін серпімді режим теориясының есептерін шешудің жуықтау әдісін қолданады, олар 1 және 2 бөлімдерде қарастырылған.
3-бөлімде ұнғылардың интерференция (өзара әсерлесу) құбылысы қарастырылады, оның маңызы бір топ ұнғымаларының жұмыс режимінің өзгеруі немесе қосылуы мен тоқтатылуының әсерінен сол қабатты пайдаланатын басқа топ ұңғымаларының түптік қысымы мен шығымы өзгереді.
2. ҚУЫСТЫ ОРТАДА ГАЗДЫҢ БЕЛГІЛЕНБЕГЕН ҚОЗҒАЛЫСЫ
2. 1 Дифференциалдық теңдеуді сызықтау (линеаризация) .
Егер сызықсыз дифференциалдық теңдеуді (1) сызықтымен ауыстырсақ, яғни
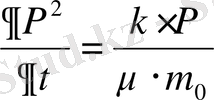


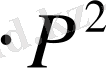 , (1)
, (1)
оны сызықтасақ, онда ол қысқарады - сызықты теңдеулер үшін дәл аналитикалық шешімдер бар. Бұл сызықты тендеудің дәл шешімдері сызықсыз үшін жуықтау болады. Дәл нақты тендеуді сызықтымен ауыстыру кезінде туатын шешімнің ағаттығын бағалау, мысалы: жуықтау шешімді дәл (нақты) тендеуде ЭЕМ-де шешумен салыстыру арқылы мүмкін болады.
Егер ұңғыға жазық радиалды ағын қарастырылатын болса, онда дипрессияның құйғышы өте тік ерекшеленеді. Осының негізінде Лейбензон теңдеудің коэффициентіндей ауыспалығын тұрақты
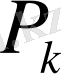 ауыстыруды ұсынды (
ауыстыруды ұсынды (
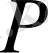 қабаттағы бастапқы) . Онда былай белгілей отырып
қабаттағы бастапқы) . Онда былай белгілей отырып
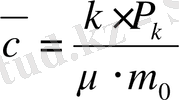 (1)
(1)
теңдеудің орнына мына теңдеуді аламыз:
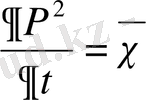


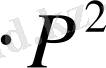 , (2)
, (2)
бұл
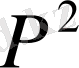 функциясына қатысты пьезоөткізгіштің сызықты теңдеуі болып табылады.
функциясына қатысты пьезоөткізгіштің сызықты теңдеуі болып табылады.
И. А. Чарный (2) теңдеудегі
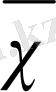 коэффициентіндегі
коэффициентіндегі
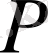 ауыспалығын мынаған ауыстырумен
ауыспалығын мынаған ауыстырумен
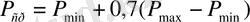 (3)
(3)
сызықтыққа келтіруді ұсынды,
мұндағы
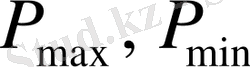 есептеу кезеңіне сәйкес газдың кеніштегі максимал және минимал
есептеу кезеңіне сәйкес газдың кеніштегі максимал және минимал
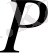 қысымы.
қысымы.
Қалыңдығы
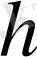 тұрақты ұзақтығы шексіз қабатта орналасқан, шексіз аз радиусты ұңғыға газ ағынының келуі туралы нақты есепті қарастырайық. Уақыттың бастапқы моментінде қабат қозбаған, яғни
тұрақты ұзақтығы шексіз қабатта орналасқан, шексіз аз радиусты ұңғыға газ ағынының келуі туралы нақты есепті қарастырайық. Уақыттың бастапқы моментінде қабат қозбаған, яғни
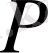 (қысым) барлық қабатта тұрақты шығыммен
(қысым) барлық қабатта тұрақты шығыммен
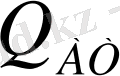 газ от алына бастайды.
газ от алына бастайды.
Бұл есепті шешу үшін сызықталған теңдеуді (3) пайдаланамыз. Газдың жазық радиалды фильтрациясы үшін ол келесі түрде жазылады:
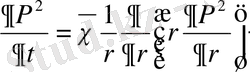 (4)
(4)
Бұл жердегі өрнек
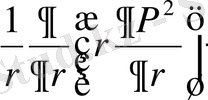 жазық радиалды ағыс үшін
жазық радиалды ағыс үшін
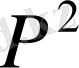 қа қатысты полярлы координаттағы Лапластың операторын көрсетеді.
қа қатысты полярлы координаттағы Лапластың операторын көрсетеді.
Тендеуді (4) бастапқы жағдайлар кезінде интегралдау керек.
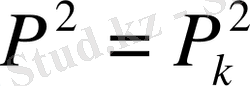

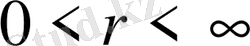 кезінде (5)
кезінде (5)
және алыс нүктелердегі шекті жағдайлар кезінде
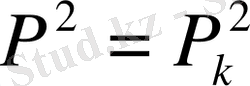

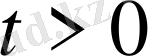 (6)
(6)
Ұңғы түбінде
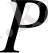 үшін жағдай щығарамыз. Жазық радиалды фильтрация үшін дифферендиалдық түрде Дарси заңынан шыға отырып жаппай (жалпы) шығым үшін өрнек жазамыз.
үшін жағдай щығарамыз. Жазық радиалды фильтрация үшін дифферендиалдық түрде Дарси заңынан шыға отырып жаппай (жалпы) шығым үшін өрнек жазамыз.
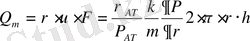
теңдеуін пайдалана отырып
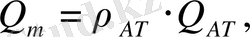
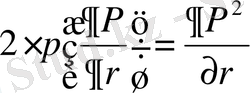 және
және
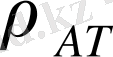 бөліп мынаны табамыз:
бөліп мынаны табамыз:
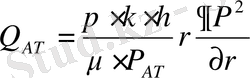 (7)
(7)
Осы арақатынастан радиусы шексіз аз газ ұңғымасының қабырғасындағы жағдайды көрсетеміз:
Ұқсастық
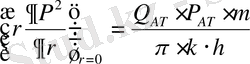 . (8)
. (8)
Осылайша қойылған есепті шешу үшін (4) теңдеу (5), (6), (8) жағдайлары кезінде интегралдануы қажет.
2. 2. Серпімді сұйық газдың фильтрациясы арасындағы ұқсастық.
Шексіз бастапқыда қозбаған қабаттан тұрақты
 бар серпімді сұйықты алудың математикалық қойылған есебі (9) теңдеумен және (10), (11) жағдайларымен берілген (көрсетілген) .
бар серпімді сұйықты алудың математикалық қойылған есебі (9) теңдеумен және (10), (11) жағдайларымен берілген (көрсетілген) .
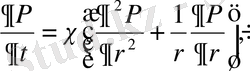 (9)
(9)
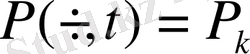
 ,
,
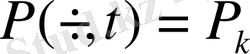
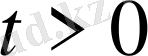 ,
,
 (10)
(10)
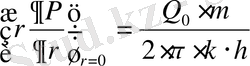 (11)
(11)
Серпімді сұйық үшін арақатынасты келтірейік және газ үшін оларды (4) -(6), (8) арақатынасымен салыстырайық.
Серпімді сұйық:
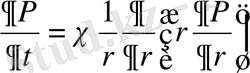 ,
,

 ,
,

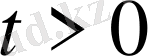 ,
,
 ,
,
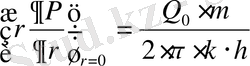 .
.
Идеал газ:
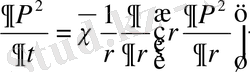 ,
,
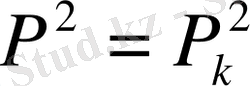
 ,
,
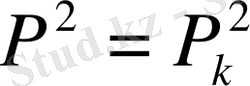
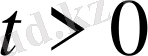 ,
,
 ,
,
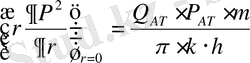 .
.
Келтірілген мәліметтерден барлық арақатынастарда идеал газ
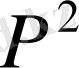 кіретіні көрініп тұр, ал бұл уақытта серпімді сұйық үшін - бірінщі дәрежеде сұйық пьезоөткізгіштік коэффициенті
кіретіні көрініп тұр, ал бұл уақытта серпімді сұйық үшін - бірінщі дәрежеде сұйық пьезоөткізгіштік коэффициенті
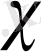
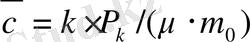 ауыстырады, газ үшін
ауыстырады, газ үшін
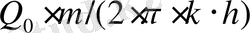 коэффициенті
коэффициенті
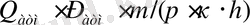 . Қалған барлық арақатынастарда бәрі ұқсас (бірдей) .
. Қалған барлық арақатынастарда бәрі ұқсас (бірдей) .
Серпімді сұйық үшін қойылған есептің шешілуі серпімді режимнің негізгі формуласы
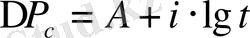 , болып табылады.
, болып табылады.
Мұндағы
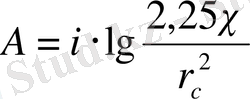 ;
;
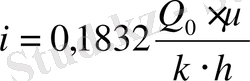
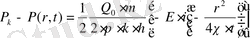 (12)
(12)
Серпімді сұйық пен газ фильтрациясыының арасындағы ұқсастық (12) формуладағы қысымды
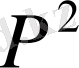 -қа
-қа
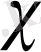 -ты
-ты
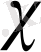 -қа
-қа
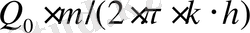 -ты
-ты
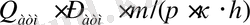 -қа ауыстыра отырып, газ үшін қойылған есептің шешімін алуға кепілдік береді.
-қа ауыстыра отырып, газ үшін қойылған есептің шешімін алуға кепілдік береді.
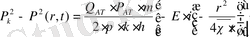 (13)
(13)
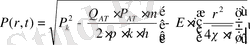 (14)
(14)
Аргументтің
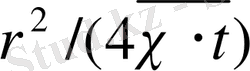 аз мәндері үшін
аз мәндері үшін
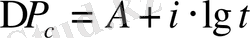 формуласына сәйкес логарифмдік функцияның интегралдық көрсеткішін ауыстыруға болады.
формуласына сәйкес логарифмдік функцияның интегралдық көрсеткішін ауыстыруға болады.
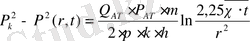 (15)
(15)
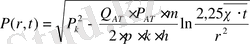 (16)
(16)
(13) -(16) теңдеулер жуық шама болып табылады, өйткені дәл емес (1) сызықты теңдеуі (4) -ті интегралдау нәтижесінде алынған.
(14) және (16) формулалар (уақыт мәндерінде
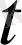 берілген кезінде)
берілген кезінде)
 сәтінен бастап тұрақты шығыммен жұмыс істейтін газды скважинаның айналасындағы
сәтінен бастап тұрақты шығыммен жұмыс істейтін газды скважинаның айналасындағы
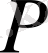 таралуын анықтайды.
таралуын анықтайды.
Ұнғыманың бастапқы жұмысынан кейінгі түптегі
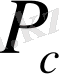 өзгеруі
өзгеруі
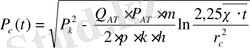 (17)
(17)
Тұрақты берілген шығымы
 бар ұңғымаға орнықпаған газ ағысының келуі туралы есепті шешіп көрейік.
бар ұңғымаға орнықпаған газ ағысының келуі туралы есепті шешіп көрейік.
Кез-келген уақыт сәтінде қозған облыс (аймақ) радиусы
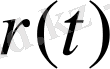 -ға тең айнала облыс болып табылады, оның ішінде
-ға тең айнала облыс болып табылады, оның ішінде
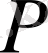 стационар (тұрақты) заң (9) бойынша таралған.
стационар (тұрақты) заң (9) бойынша таралған.
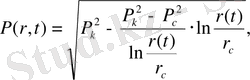
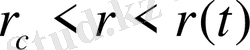 (18)
(18)
Қозған аймақ сыртында
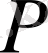 бастапқыға тең (қозған күй)
бастапқыға тең (қозған күй)

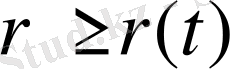 (19)
(19)
Қозған аймақта стационарлық фильтрация үшін, формула бойынша шығым үшін де өрнекті жазуға болады.
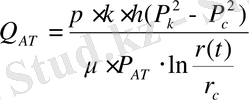 (20)
(20)
Қарастырып отырған есептегі түптік қысым
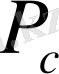 уақыт фунқциясы болып табылатынына назар аударайық.
уақыт фунқциясы болып табылатынына назар аударайық.
Кейінгі қорытыңдының жеңілденуі үшін (20) -дан мына арақатынасты тауып
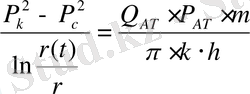
және оны қозған аймақтағы (18)
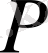 үшін формулаға қоямыз.
үшін формулаға қоямыз.
Сонда алатынымыз:
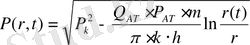 , (21)
, (21)
яғни берілген шығым мен қабат параметрлері арқылы өрнектелген
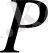 -ң таралуы.
-ң таралуы.
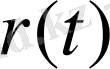 табу үщін материалдық баланс тендеуін құрамыз. Радиусы бар қабат аймағындағы
табу үщін материалдық баланс тендеуін құрамыз. Радиусы бар қабат аймағындағы
 , кезіндегі газдың бастапқы қоры
, кезіндегі газдың бастапқы қоры
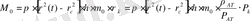 , (22)
, (22)
газдың ағымдағы қорын орташа өлшенген қысым
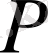 арқылы өрнектейміз:
арқылы өрнектейміз:
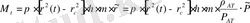
Мұнда
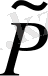 Equation. 3 орныққан фильтрацияның формуласы бойынша анықталады
Equation. 3 орныққан фильтрацияның формуласы бойынша анықталады
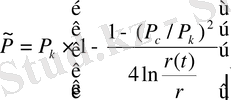 , (24)
, (24)
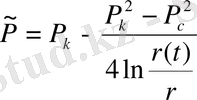 Equation. 3 . (25)
Equation. 3 . (25)
Газдың алынуы тұрақты шығыммен
 жүретін болмағандықтан
жүретін болмағандықтан
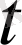 уақыт сәтіндегі алынған газ массасы
уақыт сәтіндегі алынған газ массасы
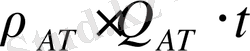 -ға тең. Осылайша
-ға тең. Осылайша
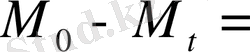
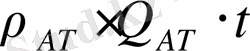 немесе (23) -(24) пайдалана отырып мынаны табамыз
немесе (23) -(24) пайдалана отырып мынаны табамыз
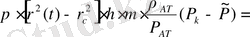
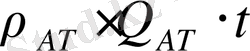 (26)
(26)
Орташа өлшенген
 қысым үшін (25) өрнекті (26) -ға және
қысым үшін (25) өрнекті (26) -ға және
 үшін (20) -ны қоя отырып мынаны аламыз:
үшін (20) -ны қоя отырып мынаны аламыз:
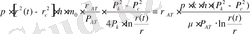
осыдан
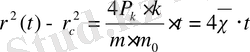 (27)
(27)
немесе
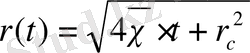 .
.
Уақыт мәні үшін, ал олар үшін
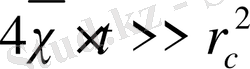 мынаған ие болады:
мынаған ие болады:
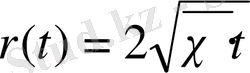 .
.
Енді (27) немесе (28) түрінде қозған облыстың қозғалу шекарасының заңдылығын біле отырып, (21) формула бойынша уақыттың кез келген сәтіндегі, қабаттың кез келген нүктесіндегі
 -ны, сонымен қатар уақыттың кез келген сәтіндегі ұнғыма түбіндегі
-ны, сонымен қатар уақыттың кез келген сәтіндегі ұнғыма түбіндегі
 -ң өзгеруін табуға болады:
-ң өзгеруін табуға болады:
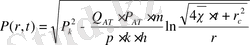 ,
,
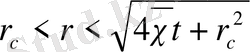 , (29)
, (29)
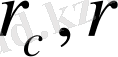

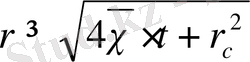 ,
,
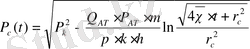 . (30)
. (30)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz