Сақиналы ұңғымалар батареясының өзара әсерлесуі және шығымдық есептеулері

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

Мазмұны

Кіріспе. 1

1 Сақиналы батарея ұңғымаларының өзара әсері. 2

1. 1 Кеніште экцентрлі орналасқан ұңғыманың шығымы. 2

1. 2 Сақиналы батерия ұңғымаларының өзара әсері. 4

1. 3 Сақиналы батареяның қосынды шығымына ұңғыма санының әсері. 7

Қорытынды8

ӘДЕБИЕТТЕР ТІЗІМІ9

Кіріспе.

Серпімді қуысты ортада серпімді сұйық пен газдың белгіленбеген фильтрациясымен әртүрлі шекті есептерін шешуге шеке туындылардағы сызықты дифференциал теңдеулері жақсы белгілі, интегралдау әдісінің көмегімен жетуге болады. Көптеген жағдайда бұлшешімдер өте үлкен болып келеді.

Ұңғымалардың интерференция өзара әсерлесу құбылысы қарастырылады, оның маңызы бір топ ұңғымаларының жұмыс режимінің өзгеруі немесе қосылу мен тоқталуының әсерінен сол қабатты пайдаланатын басқа топ ұңғымаларының түптік қысымы мен шығымы өзгереді.

Негізінен келген бұл курстық жұмыс сақиналы батарея ұңғымасының өзара әсерін түсінүге жәрдемін тигізеді.

Студенттердің курстық жұмыстарымен жеке үй тапсырмалары жоғары мамандардың білімінің сапасын жоғарлатуда

ең бір қажетті жұмыс болып саналады. Бұл кезде студенттердің жеке білімдері өте жоғары дәрежәде болады және олардың осы оқып жатқан сабақтарының нәтежесінен алған білімдерін жетілдіреді.

1 Сақиналы батарея ұңғымаларының өзара әсері.

1. 1 Кеніште экцентрлі орналасқан ұңғыманың шығымы.

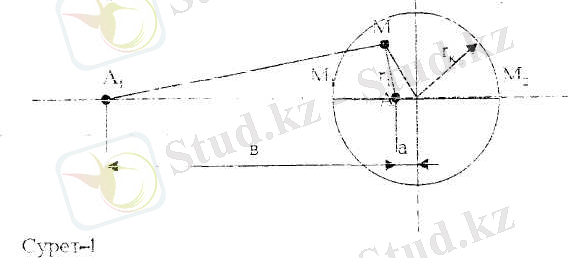
Ұңғыма радиусы r _k кеніштің центрінен а қашықтықта орналасқан делік. (1сурет) Қоректендіру контурына шағылу жасайықта, оны А- қорек көзі нүктесіне орналастырайық. Арақашықтық .

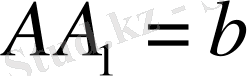М нүктесіндегі потенциал: 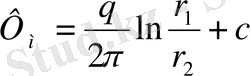(1)

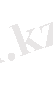
М нүктесін қоректендіру контурына (М ₁ , М ₂ ) нүктелерін ауыстырамыз. Онда 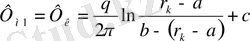(2)

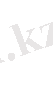
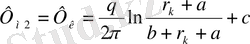(3)

(2) және (3) формуланы теңестіре отырып, мынаны аламыз.

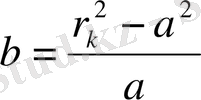(4)

(4) -ті (2) қоямыз. Сонда 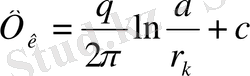(5)

М нүктесін ұңғыманың қабырғасына А орналастыра отырып мынаны аламыз. 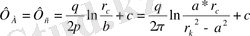(6)

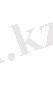
(5) -тен (6) -ны шығара отырып кеніште эксцентрлі орналасқан ұңғыманың шығымын табамыз: 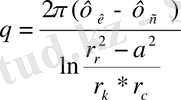(7)

а=0 кезінде (7) -ден Дюпюидің формуласы жеңіл алынады;

q= 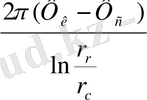(8)

1. 2 Сақиналы батарея ұңғымаларының өзара әсері.

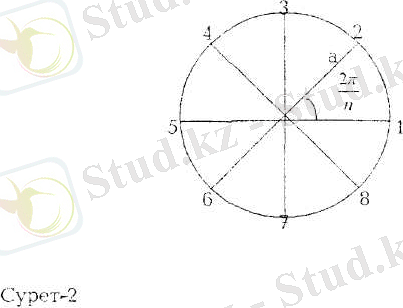
Қабаттың үлкен өтімділігі бар пайдаланушы ұңғыманың бірлескен іс-әрекетін қарастырайық, олардың 0, ұғғыма радиусы а шеңбер бойында сақиналы батерия құрайтындай етіп, оң(дұрыс) П-үшбұрышының шыңына орналасады(2-сурет) . Қабаттың қоректендіру контуры ұңғымадан сақиналы батерияның радиусынан а айтарлықтай алып түсетін қашықтықта бөлінген. Бұл кезде барлық скважиналар контурда контурдан r бірдей арақашықтықта орналасқан деп есептеуге болады.

Берілгені қоректендіру контурдағы потенциялдық функцияның Ф _к тұрақты мәні және қоректендіру контурдағы потенциометр функциясының Ф _к тұрақты мәні және де барлық ұңғыманың контурындағы Ф _к тұрақты мәні.

Сақиналы батерияның ұңғымаларына филътрациялық ағын туралы есеп, берілген радиустың а бойында бір қалыпты орналасқан жазық ағыс К және нүктелік ағыс туралы есеп. Формула бойынша: 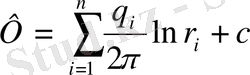(9)

Мынадай екенін табамыз:

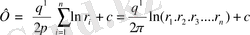(10)

Мұндағы q ¹ -батериясының кез-келген ұңғымасының шығымы r ₁ r ₂ r ₃ …r _n -барлық ұңғыма ларға дейінгі қабаттың кейбір нүктелерінің арақашықтығы.

Шекаралық шарттар

(11)

I-номерінен кейін ұңғыма контурдағы үшбұрыштікі ОО ₁ О ₂ ОО ₁ О ₃ және т. с. с, ,

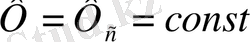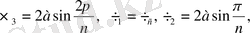
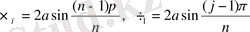(12)

(10) формулаға қолданатындай (11) және (12) шекаралық шарттарын пайдалана отырып, мынаны аламыз:

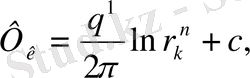(13)

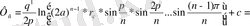
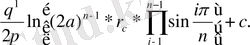= (14)

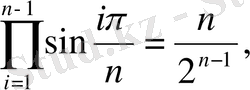екені белгілі (15)

(15) туындысының мәнін (14) формулаға қоя отырып, мынаны табамыз:

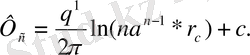(16)

(15) және (16) формуладан ұңғыманың шығымыны аламыз:

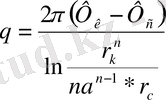
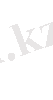(17)

(17) формула жуық шамалы. Оны ұзына бойы үлкен қабатта жұмыс істеп тұрған ұңғыма батареясына қолданған жеңіл. Мысалға, егер сұйықты сығылмайды деп қарастыруға болатын су арынды режим кезінде, егер де қабатта еріген газдың режимі орныққан болса, онда газдалған сұйық алып жатқан аудан қабаттың шекарасына дейін созылып жататынын болжамдау қиын, ол өлшемдері бойынша ұңғыма батареясының ішкі аймағының ауданынан бірнеше есе үлкен. Бірақта ол нұсқа (17) формуланы шығару негізіне жатты. Егер есептің шарты бойынша ұңғымадан қоректендіру контурына дейінгі арақашықтық батарея радиусынан а ₁ өте көп асып түспесе, онда едәуір дәл формуланы пайдаланған жөн.

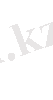
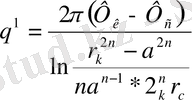(18)

(17) формуладан 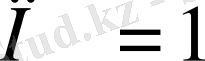кезінде (16) формула шығады.

1. 3 Ұңғымалар арасындағы арақашықтықтың олардың өзара әсерлесуіне тигізетін әсері.

(16) немесе (17) формуладағы шамаға 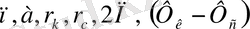өзгермеген кезде әртүрлі сандық мәндерді бере отырып, шығымның да 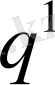әртүрлі мәндерін алып отырамыз. Батарея радиусының сандық мәндерін өзгерте отырып, және (16) немесе (17) формулаларға кіретін басқа қалған шамалар өзгермейтін кезде басқа жолдармен шығымын q өзгертетін боламыз. (16) немесе (17) формулалар көрсететіндей ұңғыманың шығымы батареяның радиусы а ₁ мен олардың санына және сол себепті ұңғымалар арасындағы ара қашықтыққа байланысты болады.

nq тең батареяның қосынды шығымы сол сияқты ұңғыма санына n және олардың арасындағы арақашықтыққа пропорционал емес. Ұңғымалардың саны n көбейген сайын әрбір ұңғыманың шығымы төмендейді, егер скважинадағы қысым өзгермейді деп қабылдаса. Бұл ұңғымалардың бір-біріне әсер етуінен түсіндіріледі-интерференциялайтын ұңғымалардың өзара әсерлесу эффектілері байқалатын болады. Орныққан күйге жеткеннен кейін ұңғымалар батареясының мүмкін болып үш жұмыс істеу жұмыс режимін көрсетейік:

Барлық ұңғымалар пайдалануға бірінші жіберілген ұңғымада болған тұрақты шығым жағдайында жұмыс істейді;
Барлық ұңғымалар қабатты игерудің бастапқы сатысында байқалған тұрақты түптік қысым кезінде жұмыс істейді;
Ұңғымалар бастапқы қысым және бірінші ұңғымадағы шығым сақталмайтындай жағдайларда пайдаланады.

Ұңғымалар ондағы қысым тұрақты ұсталып тұратын бірінші режим жағдайларында жұмыс істейді делік. Қайтадан пайдалануға жіберілген ұңғымалардың біріншісінің жұмысына әсері, жжаңа қосылған ұңғымалардың есебінен біріншідегі шығым өзгереді.

Немесе ұңғымалардың өзара әсері бұл кезде олардың режимінде тек шығымның өзгеруінен ғана сипатталады. Үшінші режим жағдайларында ұңғымалардың өзара әсері бір уақытта қысым мен шығымның өзгеруімен сипатталады. Келіскендей ұңғыманың шығымын оның қабатта жеке жұмыс істеуі кезіндегі q арқылы, ал дәл ұңғыманың топтасқан ұңғымалармен бірлескен жұмысын q ¹ арқылы белгілейік.

Өзара әсер коэффициенті шығымның ¹ ге қатынасы деп атаймыз.

(19)

Өзара әсерлесудің қосынды коэффициенті

(20)

Дөнгелек қабаттағы ұңғымалардың сақиналы батареясына қолданатын және (18) формуланың негізінде келесі мәндерге ие

(21)

(22)

Ұңғыманың радиусы есептеулер батарея радиусының а әртүрлі мәндері үшін орындалады. ЭВМ-да орындалған есептеулердің нәтижесі кестеге түсірілген.