Фазалық ауысулардың теориясы: классификация, Клапейрон-Клаузиус пен Эренфест теңдеулері, Ландау-Гинзбург тәсілдері және сегнетоэлектриктердің кванттық зерттелуі


Мазмұны.
Кіріспесі . . . 3
І тарау. Фазалық ауысулар. Олардың классификациясы . . . 6
- Бірінші тектік фазалық ауысу Клапейрон-Клаузиус теңдеуі . . . 10
- Екінші текті фазалық ауысу Эренфест теңдеуі . . . 15
ІІ тарау. Фазалық ауысудағы Ландау теориясы . . . 19
- Бірінші текті фазалық ауысу . . . 22
- Екінші текті фазалық ауысу . . . 24
ІІІ тарау. фазалық ауысулар (Гинзбург
теориясы) . . . 27
IV тарау. Кванттық теорияның көзқарасы арқылы фазалық ауысуларды зерттеу . . . 34
Қорытынды . . . 37
Пайдаланылған әдебиеттер . . . 40
КІРІСПЕ
Термодинамикада фаза деп - өздерінің қасиеттері жөнінен жүйенің біртекті бірдей бөліктерінің жинағын айтады. Фаза ұғымын мынандай мысалдар арқылы түсіндірейік. Жабық ыдыста су және оның үстінде ауа мен су буының қоспасы тұр. Бұл жағдайда біз екі фазадан тұратын жүйемен істес боламыз: бір фазаны су, ал екінші фазаны ауа мен су буының қоспасы құрайды. Егер суға бірнеше кесек мұз тастасақ, онда мұздың бұл кесектерінің бәрі үшінші фазаны құрайтын болады. Осыдан, қандайда бір заттың түрліше фазалары болып табылатынын байқаймыз. Атап айтқанда, мысалы, алмас пен графит көміртегінің түрліше қатты фазаларына жатады.
Белгілі бір жағдайларда бір заттың түрліше фазалары бір-бірімен өзара жанаса отырып, тепе-теңдікте бола алады. Екі фазаның тепе-теңдігі темперетураның тек белгілі бір интервалында жүзеге аса алады, онда да температураның әрбір мәніне тепе-теңдік орнайтын Р-қысымның белгілі бір мәні сәйкес келеді. Сөйтіп, екі фазаның тепе-теңдік күйлері (Р, Т) диограммада мына сызықпен көрсетіледі:
Р = f (Т)
Атап айтқанда, мысалы, сұйық пен оның қаныққан буының тепе-теңдік үштік нүкте температурасы мен кризистік температурасының арасындағы температуралық интервалда байқалуы мүмкін.
Екі фазалық жүйе үшін (Р, V) диограмасында Карно циклін қарастырайық. Температурасы Т изотерманың горизонталь учаскесінің шеткі нүктелері 1 және 2 цифрларымен белгіленген. 1 және 2 күйлер бір фазалы күйлер болып табылады. 1-2 кесіндісінің аралық нүктелерінің бәрі бір-бірінен зат массаларының бірінші және екінші фаза арасында бөліну арқылы айырылатын екі фазалық күйлерді кескіндейді.
Изотермиялық процесс А-В заттың қайсыбір m- массасының фазалық ауысуымен байланысты болады. Сол кезде заттың көлемі m(V
/
-V
/
1
) -ға тең өсімше алады, мұндағы V
/
1
пен V
/
-бірінші және екінші фазалардың меншікті көлемдері. Мұндай ауысу жүзеге аса алатын болу үшін, затқа mq
12-ге
тең Q
1
жыл мөлшерін беруге тиіспіз, мұндағы q
12
-T температура жағдайында 1-күйден 2- күйге ауысқан кезде жұтылатын меншікті жылу. Q
1
жылу жүйенің циклдің барысында қыздырғыштан алатын жылуын білдіреді. Суытқыш жылу С Д изотермиялық процестің барысында беріледі. Берілген жылу мөлшері мынаған тең: Q
2
=m
/
q
/
12
q
/
12
-T -
 T температура жағдайында 1-2 ауысу жылуы, ол m - С - Д процестің барысында фазалық ауысуға ұшыраған зат мөлшері. Заттың бұл мөлшерінің m-нен аз ғана айырмашылығы бар, өйткені заттың қайсыбір мөлшері адиабаталық процестің барысында фазалық ауысуға ұшырайды.
T температура жағдайында 1-2 ауысу жылуы, ол m - С - Д процестің барысында фазалық ауысуға ұшыраған зат мөлшері. Заттың бұл мөлшерінің m-нен аз ғана айырмашылығы бар, өйткені заттың қайсыбір мөлшері адиабаталық процестің барысында фазалық ауысуға ұшырайды.
Бір заттың үш фазасы (қатты, сұйық және газ тәрізді фаза, немесе екі қатты және бір сұйық фаза) температурамен қысымның бір жалғыз-ақ мәнінде тепе-теңдікте тұра алады, бұларға / Р, Т / диограмасында үштік нүкте деп аталатын сәйкес келеді. Бұл нүкте жұбымен алынған фазаларының тепе-теңдік қисықтарының қиылысында жатады.
Термодинамикада тәжірибелерге сәйкес тепе-теңдік күйде бір заттың көп болғандығын үш-ақ фазасы болатыны дәлелденеді.
Бір фазадан екінші фазаға ауысу, әдетте жасырын жылу, яғни жай жылу деп аталатын қайсыбір жылу мөлшерінің жұтылуына немесе бөлініп шығуына байланысты болады. Кристалдық модификациялардың бір түрден екінші түріне ауысып кейде жылу мөлшерін жұтылуға немесе бөліп шығаруға байланысты болмайды. Мұндай ауысулар кәдімгі бірнеше текті фазалық ауысулардан бөлек, екінші бір текті фазалық ауысулар деп аталады.
Меншікті көлемнің секірмелі өзгерісіндігі және жасырын жылудың бөлінуіндегі немесе жұтылуындағы фазалық түрлену бірінші текті фазалық ауысуға жатады.
Фазалық қайтымды процесстің түрлену термодинамикасының екінші заңы былай жазылады:
dS=
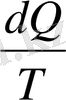 T=const теңдеуді интегралдасақ
T=const теңдеуді интегралдасақ
S
2
-S
1=
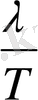 ,
мұндағы
,
мұндағы
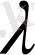 -
фазалық ауысудағы жасырын жылудың түрленуі.
-
фазалық ауысудағы жасырын жылудың түрленуі.
Бірінші текті фазалық ауысуда
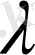
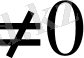 анықталады.
анықталады.
Меншікті көлемнің өзгеруінсіз және жасырын жылудың бөлінуінсіз немесе жұтылуынсыз болатын фазалық түрлену, екінші текті фазалық ауысуға жатады (dQ = 0, dV = 0)
Бірінші текті фазалық ауысуда термодинамикалық потенциалдың өзгерісі нөльге тең.
І тарау. Фазалық ауысулар. Олардың классификациясы
Егер термодинамикалық жүйеде тепе-теңдік шарттар орындалса, онда жүйенің ішкі құрлысы өзгере бастайды, фазаларда да өзгеріс байқалады, кейбір фазалар жоғалып кетуі мүмкін, кейбір фазалар жаңадан пайда болады да, фазалардың құрлысының өзгерісі фазалық ауысулар деп аталады. Фазалық ауысулар себептеріне мынандай жағдайлар жатады. Жүйенің өзгеретін параметірлерінің саны оның еркін дәрежелерінің санынан артық жағдайларда жүйенің жеке сипатамалары өте үлкен интеграл болып өзгереді, сондықтан сәйкес тұрақталмаған болып басқа фазаға өтеді.
Фазалық ауысу процестерін зерттеудің практикаға, техникаға және теорияға маңызы зор. Қатты дененің физикасының дамуына байланысты сегнетоэлектриктерді, феромагнитиктерді, асқын өткізгіштік күйлерін фазалық ауысуларды зерттеу өте қажет. Содан кейін фазалық ауысуларға қандай факторлар әсер ететінін білу керек. Бұл зерттеуге сүйеніп, фазалық ауысуды белгілі бір бағытта жүргізуін байқаймыз, мысалы, темпертураны үлкен диапозонда өзгертуге болады.
Фазалық ауысулардың территориясы қазіргі заманда екі бағытта зерттеледі. Ал, феноменологиялық теория термодинамикалық функцияларды пайдаланады және статистикалық теория фазалық ауысуларды зерттеу үшін заттың микроскопиялық құрлысын еске алады. Бұл теория қазіргі заманда толық құрылған жоқ. Сондықтан бірінші бағыт феноменологиялық теория қолданылады. Феноменологиялық теорияға академик Ландау теориясы жатады.
Осы тақырыпта феноменологиялық теорияны қарастырамыз. Әр фазаның өмір сүруі белгілі термодинамикалық жағдайларда ғана бола алады. Егер сол жағдайлар өзгерсе, онда фазалық ауысулар басталады. Кейбір жағдайда фазаны сақтау үшін сол күйді сипаттайтын параметрлерді үлкен интервалда өзгертуге болады. Мысалы: кристалды қыздырғанда температура белгісі интервалда ұлғайса да, бірақ қатты агрегаттық күйін өзгертпейді, белгілі фазасын сақтайды. Осы орындалу үшін кристалдың температурасы балқу температурасынан төмен болу керек. Одан артық болса кристалл балқуға ұшырайды басқа агрегаттық күйге көшеді: фазалық ауысулардың түрлері табиғатта, сондай -ақ физикалық және химиялық процестерде де кездеседі. Фазалық ауысуларға бірнеше мысалдар қарастырайық.
1. Фазалық ауысудағы заттың агрегаттық күйінің өзгеруінен мынандай процестерді білеміз: Булану, конденсация, кристаллизация, сублимация және т. б. Термодинамикалық тепе-теңдік шарты бойынша фаза түсінігі агрегаттық күйде адекваттық түсінік деп қолданылмайды. Сондықтан да заттың бір агрегаттық күйден басқа агрегаттық күйге ауысуымен салыстырғанда фазалық ауысулар кең көлемде көрінеді.
- Фазалық ауысуларға заттың бір аллотропиялық түрден екінші түрге өтуі жатады / графит, алмаз /. Осы жағдайда әр түрлі фазаға әр түрлі модификация сәйкес келеді. Мысалы, қатты денеде бірнеше фаза болуы мүмкін. Бұл кристалдық модификация. Әрбір модификация анықталған интервалда параметрлердің /қысым, температура және т. б. / өзгеруі тұрақты. Кристалдық модификацияның әр түрлі физикалық қасиеттері бар. Мысалы, көміртегі кристалл, графит және алмаз түрінде кездеседі. Графит жұмсақ және электр өткізгіштігі үлкен, ал алмаз - ең қатты денеге жатады. Графит пен алмаз бір-біріне қарама-қайшы заттар. Анықталған термодинамикалық шартта тұрақты күйде бір ғана кристалдық модификация болуы мүмкін. Мысалы, көміртегінің тұрақты модификациясы - грофит, алмаз модификациясы тұрақты емес болса. Ал, үлкен қысымда керісінше алмаз тұрақты модификация, графит тұрақты емес болады.
Қысымға байланысты мұздың жеті түрін білеміз. Егер қысым өте үлкен болса. Ол тұрақты модификация. Мұз VІІ 4 атмосфералық қысымда байқалады. Мұз І- ден басқа түрлері судан ауыр болып келеді.
- Физика мен техникада фазалық ауысулар арқылы заттың электрлік, магниттік қасиеттерінің өзгерісін туғызады. Мысалы фазалық ауысуда ферромагниттік Кюри температурасы болса, ал ауысу ферромагниттік фазалық ауысу деп аталады. Температураның өсуі арқылы зат поляризациялық емес күйден спонтанды полияризациялық күйге өтуі фазалық ауысуға жатады. Мұндай ауысулар сегнетоэлектрлік фазалық ауысулар деп аталады. Ал температура сегнетоэлектрлік Кюри температурасы болады.
Қазіргі заманда оң таңбалы температурада асқын өткізгіштік қасиеті бар керамикалық заттар ашылды. Үлкен қысымдарда зат шала өткізгіш күйден металл күйге өтетіні байқалған.
- Өте төменгі температурада квант механикасының заңдары орындала бастайды. Қазіргі кезде оның екі құбылысы белгілі. Олар: асқын өткізгіштік және асқын аққыштық. Бұл екі құбылыс фазалық ауысумен байланысты. Фазалық ауысулар физикалық, химиялық құбылыстарда жиі кездеседі. Сондықтан оларды өзара ажырату үшін термодинамикалық теорияны тағайындау керек.
Фазалық ауысулардың классификациясын жүйенің физикалық қасиеттерінің өзгерісі арқылы жүргізуге болады. Мысалы, көлемнің өзгерісі, фазалық ауысу нүктесінде жүйенің электрлік, магниттік термодинамикалық және басқа қасиеттерінің өзгерісі фазалық ауысулар барлық термодинамикалық параметрлерінің жиынтығын түсінеміз /қысым, температура/. Бірақ осы түрде қарастырған классификация ыңғайсыз. Сондықтан біз жалпы шаманы арнап алғанда, оның қасиеті мынандай болуы қажет: 1. Фазалық ауысулардың микроскопиялық құрылысына байланыссыз және термодинамикалық шамалар болуы керек. 2. Жүйенің фазасын нақты сипаттайтын болуы керек. Ондай шаманы термодинамикалық потенциял деп келісуге болады. Оның себебі: потенциялдың қасиетімен байланысты, ол фазаға және фазалық ауысу нүктесінде үздіксіз өзгереді. Ал басқа шамалар сол нүктеде секірмелі өзгереді /көлем, энтропея, сыйымдылық және көптеген шамалар/. Термодинамикада фазалық ауысуларды өзара ажырату үшін термодинамикалық потенциялдың дербес туындысын пайдаланады. 1933 жылы бұл әдісті бірінші рет Эренфест қолданған. Оның зерттеуі бойынша дербес туындының өзгерісі мен байланысты фазалық ауысулар екі топқа бөлінеді егер термодинамикалық потенциялдың дербес туындылары (
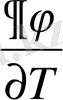 )
у
және (
)
у
және (
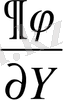 )
y
фазалық ауысу нүктесінде секірмелі өзгерсе, онда бірінші текті фазалық ауысуға жатады. Әдетте фазалық ауысу жалпылама күштің тұрақты мәні болып қарастырылады. Мысалы, қысым, термодинамикалық потенциалдың дербес туындылары (
)
y
фазалық ауысу нүктесінде секірмелі өзгерсе, онда бірінші текті фазалық ауысуға жатады. Әдетте фазалық ауысу жалпылама күштің тұрақты мәні болып қарастырылады. Мысалы, қысым, термодинамикалық потенциалдың дербес туындылары (
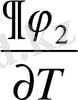 )
y
, (
)
y
, (
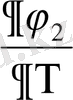 )
y
, (
)
y
, (
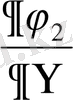 )
T
және (
)
T
және (
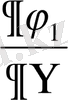 )
T
бірінші текті фазалық ауысумен сипатталады. Бірінші текті фазалық ауысу үшін термодинамикалық потенциялдың бірінші дербес туындылары фазалық ауысу нүктесінде секірмелі өзгерсе, онда теңдеу былай өрнектеледі. T=T
0
; Y=Y
0
.
)
T
бірінші текті фазалық ауысумен сипатталады. Бірінші текті фазалық ауысу үшін термодинамикалық потенциялдың бірінші дербес туындылары фазалық ауысу нүктесінде секірмелі өзгерсе, онда теңдеу былай өрнектеледі. T=T
0
; Y=Y
0
.
(T) =(
) y
- (
) y
,
0 (1. 1)
(Y) =(
) T
- (
) T

0 (1. 2)
0 2
0 бірақ есте болу керек. Термодинамикалық потенциялдардың өз фазалық ауысу нүктесінде үздіксіз өзгереді. (1. 1) және (1. 2) шарттары орындалатын фазалық ауысулар бірінші текті фазалық ауысулар деп аталады.
Егер жүйенің термодинамикалық потенциялдан алынған бірінші дербес туындылары фазалық ауысу нүктесінде үздіксіз өзгеріп, ол екінші дербес туындылары секірмелі өзгерсе, онда екінші текті фазалық ауысуына жатады.
(T) = (
) y
- (
) y
, = 0 (1. 3)
(Y) =
(
) T
- (
) T
= 0 (1. 4)
(T, T) = (
) y
- (
) y
,
0 (1. 5)
(Y, Y) =(
) T
- (
) T

0 (1. 6)
(T, Y) =(
) T
- (
) T

0 (1. 7)
(1. 3), (1. 4), (1. 5), (1. 6), (1. 7) шарттары орындалатын фазалық ауысулар, екінші текті фазалық ауысулар деп аталады. Бұдан фазалық ауысудың бірінші және екінші түрі термодинамикалық потенциялдық дербес туындылары арқылы анықталатын, фазалық ауысу нүктесінде секірмелі өзгеретінін байқаймыз.
Фазалық ауысу анықталған T = T
0
, температурада және жалпыланған күштің Y = Y
0
анықталған мәнінде өтеді. Термодинамикалық потенциялдың туындысы осы нүктеде фазалық ауысудың түрін анықтайды. Қазіргі кезде көптеген жағдайлар белгілі
 интервалда T = T
0
анықталған температурада фазалық ауысу болады. Мұндай ауысулар көмескі ауысулар деп аталады және практикалық мәнге ие болады. Осындай ауысулар үшін бір нүктеде емес температуралық интервалда термодинамикалық потенциялдың туындысы өзгереді. Көмескі фазалық ауысулар үшін Эренфест классификациясы жарамайды. Эренфест классификациясы көптеген жағдайларда толық емес және нақты фазалық ауысуды схемалық түрде жояды. Барлығы нақты практикада шекаралық жағдайлар арасында фазалық ауысулар кездеседі.
интервалда T = T
0
анықталған температурада фазалық ауысу болады. Мұндай ауысулар көмескі ауысулар деп аталады және практикалық мәнге ие болады. Осындай ауысулар үшін бір нүктеде емес температуралық интервалда термодинамикалық потенциялдың туындысы өзгереді. Көмескі фазалық ауысулар үшін Эренфест классификациясы жарамайды. Эренфест классификациясы көптеген жағдайларда толық емес және нақты фазалық ауысуды схемалық түрде жояды. Барлығы нақты практикада шекаралық жағдайлар арасында фазалық ауысулар кездеседі.
1. 1. Бірінші текті фазалық ауысу. Клапейрон - Клаузис теңдеуі.
Бірінші текті фазалық ауысу үшін термодинамикалық потенциялдың бірінші туындысы фазалық ауысу нүктесінде секірмелі өзгереді. Бұл фазалық ауысуды жақсы түсіну үшін физикалық интерпретацияны қарастырамыз. Ол үшін термодинамикалық қатынасты пайдаланамыз.
(
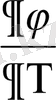 )
y
= -S және (
)
y
= -S және (
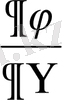 )
T
=X
)
T
=X
Бірінші текті фазалық ауысудың анықтамасын өрнектеп жазсақ, мына теңдеулерді аламыз.
 (T) =-(S
2
-S
1
) = -
(T) =-(S
2
-S
1
) = -
 S
S
 0 (1. 8)
0 (1. 8)
 (Y) = X
2
- X
1
=
(Y) = X
2
- X
1
=
 X
X
 0 (1. 9)
0 (1. 9)
бұл ауысуда жүйенің энтропиясы жалпы сыртқы параметрлері секірмелі өзгереді. Мысалы X=V, V=P болса, онда бірінші текті фазалық ауысуда көлем секілді өзгереді. Оған агрегаттық күйлердің алмасуы жатады. Сонда теңдеу былай өрнектеледі.
 (P) =V
2
-V
1
=
(P) =V
2
-V
1
=
 V
V
 0 (1. 10)
0 (1. 10)
Термодинамиканың екінші бастамасына сәйкес энтропияның өзгерісі жылудың өзгерісімен байланысты болады.
 Q
0
= T
0
Q
0
= T
0
 S, (1. 11)
S, (1. 11)
мұндағы
 Q
0
-фазалық ауысудың жылуы оның фазалық ауысудың жасырын жылуы деп те атайды. Мысалы булану жылуы. Сонымен фазалық ауысудың бірінші түрінде жылу не жұтылады, не бөлініп шығады.
Q
0
-фазалық ауысудың жылуы оның фазалық ауысудың жасырын жылуы деп те атайды. Мысалы булану жылуы. Сонымен фазалық ауысудың бірінші түрінде жылу не жұтылады, не бөлініп шығады.
Термодинамиканың негізгі теңдеуінен жүйенің ішкі энергиясының өзгерісі фазалық ауысу нүктесінде мынаған тең.
 U =T(S
2
-S
1
) - P(V
2
-V
1
)
U =T(S
2
-S
1
) - P(V
2
-V
1
)
 0 (1. 12)
0 (1. 12)
Бұл теңдеуде фазалық ауысу нүктесінде ішкі энергия секірмелі өзгеретінін байқаймыз. Фазалық ауысу температурасы тұрақты болса (dT 0 = dT = 0), онда жүйенің жылу сыйымдылығы өте үлкен мөлшерде секірмелі өзгереді.
С
р
= (
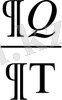 )
p
=T(
)
p
=T(
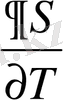 )
p
,
)
p
,
 C
p
C
p
 (1. 13)
(1. 13)
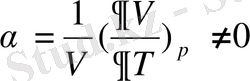 ,
,
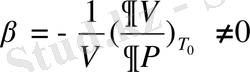 (1. 14)
(1. 14)
- коэффиценттері де секірмелі өзгереді. График түрде анықталған нәтижені келтірейік.
S V C
P,
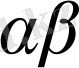

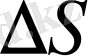


T T T
T 0 T 0 T 0
- сурет.
1-сурет. Бірінші текті фазалық ауысудағы нүктеге жақын физикалық шаманың өзгерісі. Бірінші текті фазалық ауысулар бағынатын теңдеуді Клапейрон-Клаузиус теңдеуі деп атайды. Оны табу үшін екі фазада орналасқан бір компонентік жүйеге химиялық тепе-теңдік пайдаланайық.
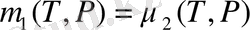 (1. 15)
(1. 15)
Бұл жерде
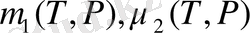 бірінші және екінші фазада бөлшекке арналған термодинамикалық потенциял. Сонымен фазалық ауысу (1. 15) қатынасты дифференциалдап, мына теңдеуді аламыз.
бірінші және екінші фазада бөлшекке арналған термодинамикалық потенциял. Сонымен фазалық ауысу (1. 15) қатынасты дифференциалдап, мына теңдеуді аламыз.
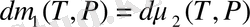 немесе
немесе
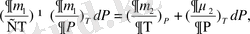 Equation. 3 )
Equation. 3 )
бұдан
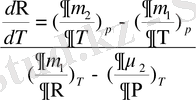 (1. 16)
(1. 16)
егер -S= (
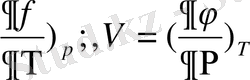 Equation. 3 ) еске алсақ,
Equation. 3 ) еске алсақ,
онда
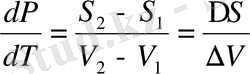 (1. 17)
(1. 17)
немесе
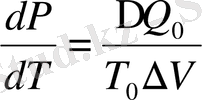 (1. 18)
(1. 18)
- фазалық ауысудың жылу саны (1. 17), (1. 18) теңдеулері Клапейрон- Клаузис теңдеуі деп аталады және бірінші текті фазалық ауысудың негізгі теңдеуі болып саналады. Клапейрон - Клаузиус теңдеуі фазалық тепе-теңдік сызығының дифференциялдық теңдеуі болып келеді. Осы теңдеуді талдайық.
Төменгі температурада термодинамиканың үшінші бастамасына сәйкес
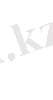
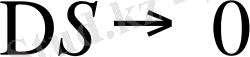 егер
егер
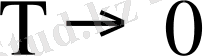 , онда (1. 18) теңдеу былай жазылады.
, онда (1. 18) теңдеу былай жазылады.
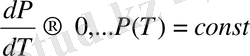 (1. 19)
(1. 19)
Графиктік түрде P=P(T) төменгі температурада тепе-теңдік сызығының жанамасы горизонталь сызық болады. Кез келген жүйеге арналған Клапейрон-Клаузиус теңдеуі мына түрде жазылады.
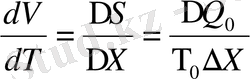 (1. 20)
(1. 20)
бір компонентті екі фазалық жүйеге арналған жалпы Клапейрон-Клаузиус теңдеуі. Егер Клайперон-Клаузиус теңдеуін мына түрде жазылады.
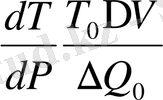 (1. 21)
(1. 21)
онда бұл теңдеу фазалық ауысудың температурасының өзгерісін қысыммен байланыстырады. Бұл өзгеріс көлемнің
 өзгерісімен және фазалық аусудың жасырын
өзгерісімен және фазалық аусудың жасырын
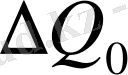 жылумен байланысты. Егер фазалық ауысу дененің қыздыруымен байланысты болса,
жылумен байланысты. Егер фазалық ауысу дененің қыздыруымен байланысты болса,
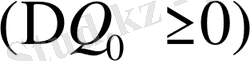 онда
онда
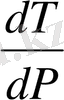 шаманың таңбасы көлемнің
шаманың таңбасы көлемнің
 өзгерісі арқылы анықталады. Көптеген заттар үшін
өзгерісі арқылы анықталады. Көптеген заттар үшін
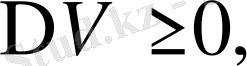 онда
онда
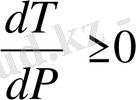 болады. Қысым неғұрлым ұлғайса, соғұрлым фазалық ауысу температурасы өседі. Егер
болады. Қысым неғұрлым ұлғайса, соғұрлым фазалық ауысу температурасы өседі. Егер
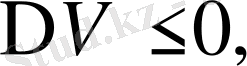 онда
онда
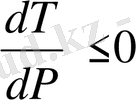 . Қысым неғұрлым ұлғайса, соғұрлым фазалық ауысу температурасы төмендейді. Бұл жағдай мұзға, висмутқа арналған. Бірінші текті фазалық ауысуға заттың агрегаттық күйінің өзгерісі жатады: қатаю, булану, конденсациялану. Мысалы:
. Қысым неғұрлым ұлғайса, соғұрлым фазалық ауысу температурасы төмендейді. Бұл жағдай мұзға, висмутқа арналған. Бірінші текті фазалық ауысуға заттың агрегаттық күйінің өзгерісі жатады: қатаю, булану, конденсациялану. Мысалы:
Қайнау. Қайнау фазалық ауысуда заттың агрегаттық сұйық күйден газ күйіне айналуы болып келеді. Ол белгілі қысым және температурада өтеді, жүйеге жылу
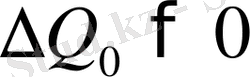 келтіріледі, көлемі ұлғаяды. Сондықтан
келтіріледі, көлемі ұлғаяды. Сондықтан
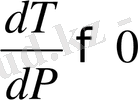 фазалық ауысу температурасы қысымға тәуелді ұлғаяды. Мысалы: Егер қысым 15 атмосфера болса, онда қайнау температурасы 200
0
С, егер қысым 80 атмосфера болса, онда 300
0
С. Анықталған сыртқы қысым анықталған қайнау температурасына сәйкес келеді. Бұл қысым қанығу буының қысымы деп аталады. Мысалы судың қанығу буының қысымы 100
0
С.
фазалық ауысу температурасы қысымға тәуелді ұлғаяды. Мысалы: Егер қысым 15 атмосфера болса, онда қайнау температурасы 200
0
С, егер қысым 80 атмосфера болса, онда 300
0
С. Анықталған сыртқы қысым анықталған қайнау температурасына сәйкес келеді. Бұл қысым қанығу буының қысымы деп аталады. Мысалы судың қанығу буының қысымы 100
0
С.
Бір уақытта екі фазаның /сұйық және бу/ болу фазалық тепе-теңдік қисықтарының нүктелеріне сәйкес келеді. Қайнау сұйық күйден газ күйіне тез өтеді. Тағы да бір порцесс бар сұйықтан буға өтетін, бұл процесті булану деп атайды. Кез келген температурада бола береді.
Балқу әрбір қатты дене агрегаттық сұйық күйден өтеді, егер температура үлкен болса. Мұндай фазалық ауысу балқу деп аталады және ол бірінші текті фазалық ауысуға жатады. Критикалық дене үшін балқу температурасы деп аталатын анықталған температурада балқу болады. Бұл қасиет кристалдық қатты дененің бір түрі аморфты денелерден ажыратуға ықпал етеді.
Балқу қысымның өзгерісіне байланысты. Қысым өзгерген кезде балқу температурасында өзгереді. Қайнаудан айырмашылығы қысымның өсуі әрқашанда температураның өсуімен байланысты. Сондай-ақ, балқу температурасы қысымның өсуі кезінде өсе бермей төмендеуі де мүмкін. Бұл қысым кезінде көлемнің өзгеруіне байланысты. Қатты денеде балқу кезінде көлем өседі, (
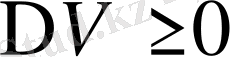 ) сондықтан Клапейрон - Клаузис теңдеуіне сәйкес
) сондықтан Клапейрон - Клаузис теңдеуіне сәйкес
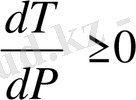 . Қысым өскен кезде балқу температурасы да өседі. Мынандай заттарды мысалы, мұз, чугун, висмут балқығанда көлемдері азаяды. (
. Қысым өскен кезде балқу температурасы да өседі. Мынандай заттарды мысалы, мұз, чугун, висмут балқығанда көлемдері азаяды. (
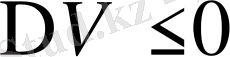 ), сондықтан
), сондықтан
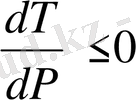 . Осындай денелерде қысым ұлғайса, балқу температурасы төмендейді. Көп заттарды
. Осындай денелерде қысым ұлғайса, балқу температурасы төмендейді. Көп заттарды
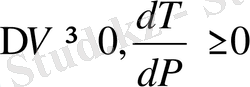 жағдайлары орындалады.
жағдайлары орындалады.
1. 2. Екінші текті фазалық ауысулар. Эренфест теңдеуі.
Екінші тектілі фазалық ауысу үшін фазалық ауысу нүктесінде термодинамикалық потенциялдың бірінші туындысы үздіксіз, ал екіншісі секірмелі өзгерді. (1. 3) . (1. 4), теңдеулерді пайдаланып келесі теңдеуді жазамыз.
 (T) =S
2
-S
1
=
(T) =S
2
-S
1
=
 S=0 (1. 21)
S=0 (1. 21)
 (Y) = X
2
- X
1
=
(Y) = X
2
- X
1
=
 X=0 (1. 22)
X=0 (1. 22)
Екінші текті фазалық ауысуда жүйенің энтропиясы және жалпы сыртқы параметрлері үздіксіз өзгереді. Сондықтан бұл фазалық ауысуларда жылу жүйеге келтірілмейді және алынбайды.
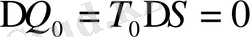
Термодинамикалық потенциялдың екінші туындыларының фазалық өту нүктесіндегі өзгерісі былай өзгертіледі.
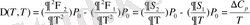 (1. 23)
(1. 23)
мұндағы
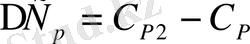 фазалық ауысу нүктесіндегі меншікті жылу сыйымдылық. (1. 6), (1. 7) теңдеулерді пайдаланып, келесі теңдеулерді аламыз.
фазалық ауысу нүктесіндегі меншікті жылу сыйымдылық. (1. 6), (1. 7) теңдеулерді пайдаланып, келесі теңдеулерді аламыз.
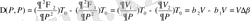
(1. 24)
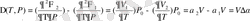 (1. 25)
(1. 25)
мұндағы
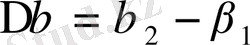 ;
;
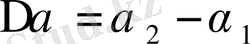 фазалық ауысу нүктесіндегі изотермиялық ұлғаю коэффициенті
фазалық ауысу нүктесіндегі изотермиялық ұлғаю коэффициенті
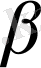 және термиялық сығылу коэффициенті
және термиялық сығылу коэффициенті
 . Сонымен екінші текті фазалық ауысуда фазалық ауысу нүктесінде энтропия, көлемі үздіксіз өзгереді. Ал жылу сыйымдылық, ұлғаю және сығылу коэффициенттері секірмелі шектелген мөлшерде өзгереді. График түрінде осы байланысты келтірейік.
. Сонымен екінші текті фазалық ауысуда фазалық ауысу нүктесінде энтропия, көлемі үздіксіз өзгереді. Ал жылу сыйымдылық, ұлғаю және сығылу коэффициенттері секірмелі шектелген мөлшерде өзгереді. График түрінде осы байланысты келтірейік.
S V C
P,
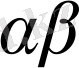
T T T
T 0 T 0 T 0
Сурет 2. Екінші текті фазалық ауысудағы нүктеге жақын физикалық шаманың өзгерісі.
Бұл физикалық ауысуға заттың ферромагниттік күйінен парамагниттік күйіне өтуі, дұрыс өткізгіштік күйден асқын өткізгіштік күйге өтуі жатады. Екінші текті фазалық ауысуға сәйкес келетін температураны
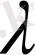 -нүкте немесе Кюри температурасы деп атайды.
-нүкте немесе Кюри температурасы деп атайды.
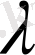 - нүкте фазалық ауысу нүктесіне жақын физикалық шама изобаралық С
р
сыйымдылықтың өзгерісінің графигі гректің
- нүкте фазалық ауысу нүктесіне жақын физикалық шама изобаралық С
р
сыйымдылықтың өзгерісінің графигі гректің
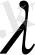 әріпіне ұқсас.
әріпіне ұқсас.
Фазалық ауысу температурасы сыртқы жағдайлармен байланысты, олар өзгерсе температурада өзгереді. Бұл жағдай бірінші текті фазалық ауысуда байқалады. Кейбір кезде сыртқы жағдайлардың өзгерісі фазалық ауысудың түрінің өзгерісіне келтіріледі. Мысалы екінші текті фазалық ауысу бірінші тектілі фазалық ауысуға өтеді. Осы жағдайдағы фазалық ауысу температурасын кризистік Кюри температурасы немесе кризистік
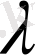 -нүктесі деп атайды. Т
0к
арқылы белгіленеді.
-нүктесі деп атайды. Т
0к
арқылы белгіленеді.
Т 0к температураға бірінші түрлі фазалық ауысу жақын және екінші түрлі фазалық ауысу жақын шектеуге болады. Бірінші жағдайда екінші текті фазалық ауысуға жақын бірінші текті фазалық ауысу, ол екінші текті фазалық ауысуға жақын екінші текті фазалық ауысу дейміз.
Екінші текті фазалық ауысудың екінші түрінің термодинамикалық теориясын Эренфест қарастырған, оның негізгі мақсаты: фазалық ауысу нүктесінде әр түрлі физикалық шамалардың ( меншікті жылу сыйымдылық,
 ,
,
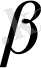 - коэффиценттер) арасындағы байланысты анықтау. Екінші текті фазалық ауысуда энтропия және көлем үздіксіз өзгереді, Клапейрон-Клаузиус теңдеуі фазалық ауысу нүктесінде анықталмағандықты береді.
- коэффиценттер) арасындағы байланысты анықтау. Екінші текті фазалық ауысуда энтропия және көлем үздіксіз өзгереді, Клапейрон-Клаузиус теңдеуі фазалық ауысу нүктесінде анықталмағандықты береді.
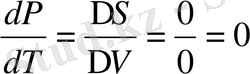
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz