Қатты денелер жайлы түсінік

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 38 бет
Таңдаулыға:

М а з м ұ н ы
Кіріспе 3
... ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ...
... ... ... ... ... ... ... ... .. ... ..
І-тарау. Қатты денелер және олардың деформациялары 6
... ... ... ... ... .
1.1. Қатты денелер жайлы түсінік 6
... ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ...
1.2. Қатты денелердің серпімді деформациясы 18
... ... ... ... ... ... ... ... .. ... ..
1.3. Қатты денелердің пластикалық деформациясы 29
... ... ... ... ... ... ... ... .
ІІ-тарау. Стерженьде серпімді толқындардың таралуын зерттеу ... . 39
2.1. Серпімді толқындар 39
... ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ...
... ... ...
2.2. Толқын теңдеуі 43
... ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ...
... ... ... ... ...
2.3. Стерженьде серпімді толқындардың таралуы 44
... ... ... ... ... ... ... ... .. ..
Қорытынды 70
... ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ...
... ... ... ... ... ... ... ...
Әдебиеттер 71
... ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ...
... ... ... ... ... ... ... ... .
Қосымшалар 72
... ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ...
... ... ... ... ... ... ... .

Кіріспе

Дүниені танудың арнайы құралы болатын математикалық модельдеу ұғымы
кең мағынаға ие. Зерттеушінің объекттіге байланысты танымы модель болады.
Модельдің түрлері көп. Математикалық модель тілі қоршаған дүние мен
абстракты математиканы байланыстыратын звено болып табылады.
Қоршаған ортамен араласып, қарым-қатынас жасаудың нәтижесінде адам өз
танымына қарай модель құрайды. Танымдық процесс зерттелінетін (танылатын)
объектіге және зерттеуші (танушы) субъектіге байланысты. Зерттелінетін
объектіде болып жатқан оқиғаны бақылап, керек болса оқиғаға кірісіп, қойған
сұрақтарына жауап алумен қатар, объектіге қатысты информацияларда жинақтап,
қорытып, субъект пен объектіге тән құбылысты түсініп, өзінің көзқарасын
белгілі бір формада бекітеді. Осы затқа тән нақтылы информацияларға
негізделген зерттеушінің субъективтік танымы – объектінің моделі болып
есептелінеді.
Танымдық процесстің негізгі қызметі – информацияны жинау, сақтау және
қорыту болса, осылар модельдеудің негізі сипаттамасын береді.
Модельдеуді жалпы үлкен екі топқа бөледі: материалдық (заттық) және
идеалдық. Материалдық модельдеу – зерттелінетін обьектің геометриялық,
физикалық, динамикалық және функциональдық сипаттамасына негізделеді.
Сондықтан материалдық таным физикалық және аналогтық болып екі топқа
бөлінеді.
Физикалық модельдеуге – ұқсастық теория негізінде нақты объектінің
кішірейтілген немесе үлкейтілген көшірмесін қолданып, лабораториялық
жағдайда процессті қайталап, тәжірибе жасап ұғу жатады.
Аналогтік модельдеуге – зерттелінетін объектілердің физикалық табиғаты
әртүрлі құбылыстарда жүретін процесстердің арасындағы байланысты білдіретін
ұқсастық теорияны қолданып, зерттеу жатады.
Мұндай процесстер бірдей математикалық теңдеумен, немесе логикалық
сызбалармен беріледі. Бұл екі типтес модельдер берілген объектілердің
заттық баламасына негізделген, өзара геометриялық, физикалық және басқа
сипаттамаларымен байланыста қарастырылады. Сондықтан материалдық модельдеу
өзінің табиғаты жағынан эксперименттік тәсілге жатады.
Заттық модельдеуден идеалдық модельдеу принципі мүлде басқа. Заттық
зерттеу объекті мен модельдің материалдық аналогиясына негізделсе, идеалдық
зерттеу танымдық процесстің негізінде құрылған ойдың, идеалдың
аналогиясының жемісі болып табылады.
Сөйтіп, идеалдық модельдеу теориялық сипаттамадан тұрады да,
интуитивтік және таңбалық болып екіге бөлінеді. Интуитивтік модельдеу
дегеніміз – зерттелетін объекті мен зерттеушінің сезім мүшелеріне әсер
етеуіне байланысты топшыланған информациялардың жиынтығы. Таңбалық модель –
зерттелінетін объектіге қатысты информацияны белгілі бір тәртіпте сүйеніп,
таңбаларға түрлендіріп, мысалы, сүлбеге, графикке, сызбаға, формулаға, т.б.
таңбаларға жинақтау.
Таңбалық модель құрылымен түзейтін элементтер заңдылыққа, алгоритмге
бағынып, өзіне тән ережелер жүйесінде жұмыс істейді. Математикалық модель –
таңбалық танымның негізіне жатады.
Математикалық модельді бірнеше түрге классификациялауға болады. Егер
процеске кездойсоқ факторлар әсер етсе стохастикалық модель, ал сырттай
әсер ететін факторлардың эффектілігі ескерімесе детерминальдық модель
делінеді. Күйді сипаттайтын функциялар уақытқа байланысты өзгерсе
динамикалық, ал күйді сипаттамаларын беретін шамалар уақыт өзегерісіне
қатысы жоқ болса стационарлық модель деп айтылады.
Қазіргі таңда математикалық модельдеу әдістері ғылымның түрлі
салаларында қолдануда. Атап айтқанда химия, билогия, физика және т.б.
Қазіргі заманғы технологиялық процестерде көптеген стержендік құрылым
элементтері әр түрлі күштер әсерінде жұмыс істейді. Мұндай әсер
көздерінен стержендік құрылым элементтерінде өте күрделі
кернеулік–деформациялық жағдайлар туындайды. Олардың табиғатына құрылым
элементтерінің қаншалықты ұзақ мерзімге төзетінділігі, беріктілігі, тікелей
байланысты болады.
Мұндай күрделі құбылыс технологиялық үрдістертің үздіксіз, мінсіз
сапалы жұмыс жасауына өз әсерін тигізбей қоймайды.
Дипломдық жұмыс тақырыбының өзектілігі тұрақты күш көздері әсерінде
жұмыс жасайтын, стержендік құрылым элементтерінде таралатын температураны
есептейтін сандық алгоритмдік әдісін құру. Алынған нәтижелерді талдау және
қорытындылау.
Дипломдық жұмыс құрылымы кіріспеден, екі тараудан, қорытындыдан,
әдебиеттер тізімінен және қосымшадан құрылған.

І ТАРАУ. ҚАТТЫ ДЕНЕЛЕР ЖӘНЕ ОЛАРДЫҢ ДЕФОРМАЦИЯЛАРЫ

1.1 Қатты денелер жайлы түсінік

Қатты денелер өздерінің физикалық қасиеттері жағынан бірінен-бірінің
өте үлкен айырмашылықтары бар екі топқа бөлінеді: кристалл денелер және
аморф денелер.
Заттың кристалл күйінің негізгі белгісі – оның анизотропиялығы.
Анизотропия деп, бір текті дененің әр түрлі бағытта қасиеттері түрліше
болатындығына айтады. Мысалы, кристалл дененің жылулық ұлғаю коэффициенті
әр түрлі бағытта түрліше болады. Кристаллдардың механикалық, оптикалық
және электрлік қасиеттері әр түрлі бағытта бірдей болмайды. Кристалдың
өзіне тән сыртқы белгісі – оның геометриялық формасының дұрыс болатындығы.
Терезе шынысының бетіне су қатқанда байқалатын мұз кристаллдардың
геометриялық дұрыс формалы өрнектері және қардың жеке ұлпаларының дұрыс
формалары жалпыға белгілі. Кристаллдардың жан-жағы айнадай жазық болып
келеді. Ол жазық жақтар бірімен-бірі түзу қырлар және үшкір бұрыштар жасап
қиылысады. Әдетте жақтар біріне қарағанда бірі симетриялы болып орналасады.
Мысалы, кварц ұштары алты жақты пирамидалар болып келген алты жақты призма
түрінде болып кристаллданады (Сурет 1.1.1). Ашудас октаэдр пішінінді (Сурет
1.1.2), ал қара тікен тұз (тас тұз) куб пішінді болып кристаллданады. Бір
кристаллды заттың әр түрлерінде оның жақтарының арасындағы бұрыштар еш
уақытта өзгермейді.

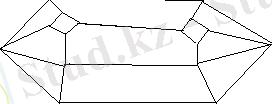
Сурет 1.1.1. Кварц кристалы.

Қатты аморф денелер изотропты болады, яғни олардың қасиеттері барлық
бағтта бірдей болады.
Кристаллдың жазықтықтары белгілі бір бағытта орналасады, сындырғанда
олар көбінесе осы жазықтықтардың бойымен жарылады. Мысалы, тас тұзының
кристаллдары ұрғанда өз ара перпендикуляр

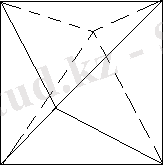
Сурет 1.1.2. Ашудас кристалы.

жазықтықтардың бойымен жарылып сынады, сонда сынғаннан кейінгі тас тұзының
кесектері параллелепипед формалы болады; слюда жұқа-жұқа пластинкаларға
бөлінеді. Ал аморф денелердің сынған жерлері ойлы-қырлы болады; жарылып
сынған шыны ұсақтарының белгілі бір формасы болмайды.
Кристалл денелер мен аморф денелердің балқу, яғни қатты күйден сұйық
күйге өту, процестері түрліше болады. Әрбір кристалл дененің өзіне тән
белгілі бір тұрақты балқу нүктесі болады. А-қисығы (Сурет 1.1.3) кристалл
денені бір қалыпты қыздырғанда оның балқу кезіндегі температурасының
уақытқа байланысты қалай өзгеретіндігін көрсетеді. Қисықтың bc бөлігі
кристалды қатты күйінде қыздыруды көрсетеді. Тбол температурасына жеткенде
дененің әрі қарай қызуы тоқталды, өйткені денеге берілетін жылудың
барлығы оны қатты күйден сұйық күйге айналдыруға жұмсалады (балқу жылуы). D
нүктесі қатты күйден сұйық күйге айналған кезін көрсетеді. Қисықтың әрі
қарай жоғарлайтын бөлігі сұйықтың қызғанын көрсетеді. Мұздың еру (балқу)
сипаты осындай болады. Мұздың еру кезіндегі температурасы, ол еріп тегіс
суға айналғанша өзгермей, 00 С-қа тең болып тұрады. Аморф дене бір қалыпты
қызғанда оның температурасының уақытқа байланысты қалай өзгеретінін
кескіндейтін В қисықтың (Сурет 1.1.3) дененің жұмсауына сәйкес жері ғана
көбірек майысады; аморф дене қатты күйден сұйық күйге біртіндеп өтеді.
Жалпы алғанда бұл жағдай қатты аморф денені аса тұтқыр сұйыққа жақындатады.

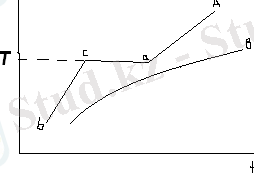
Сурет 1.1.3. Кристалл қатты дене (А) мен аморф қатты дене (В)
температураларының уақытқа байланысты өзгеруі.

Шыны, шыны тәрізді әр түрлі заттар, шайыр, битум және т.б. денелер
аморф денелер болып табылады. Балқытылған кристалл затты суытқанда кейде
шыны тәрізді күй пайда болады. Жайлап суытып жасырын балқу жылуын бөліп
шығармай және затты кристаллдық фазасына өткізбей, оның температурасын
балқу нүктесінен де төмен температураға жеткізуге болады. Алайда, мұнда
заттың тұтқырлығы соншалықты артып, ол әдеттегі сұйыққа атымен ұқсамай,
шыны тәрізді болады. Мұндай зат аса суытылған сұйық деп аталады. Аса
суытылған сұйық тұрақты болмайды: бара-бара онда кристаллдану процессі
жүреді. Кейінгі кездерде полимерлер деп аталатындарды жасайтын органикалық
қосылыстардан тұратын аморф заттарға айрықша көніл бөлінетін болды. Бұларда
неғұрлым қарапайым қосылыстағы молекулалар (маномерлер) топ-топ (полимер)
болып бірігеді. Мысалы, С2Н4О-мономерден (паральдегидтен) полимер
(ацетальдегид) жасалады; бұл ацетальдегидтен әрбір молекуласы
паральдегидтің үш молекуласынан (С2Н4О)3 құралады. Полимерленудің
мономердің бірнеше мың молекуласы бірігіп, бір топ, әдетте бау тәрізді топ,
жасалатын жоғары дәрежесінің де кездесуі мүмкін. Осындай полимерлерден
құралатын қатты аморф дене молекулалардың бау тәрізді шумағы болып
табылады. Нағыз және жасанды каучук, тағы басқа пластмассалар осыған мысал
болады.
Былай қарағанда қатты кристалл денелердің саны онша көп болып
көрінбеуі мүмкін. Алайда, анығында сыртқы формасының симметриялығы және
анизотропиялығы тікелей байқалатын денелердің ғана құрылысы кристалды
құрылыс емес. Кварцтың табиғи кристалы (тау хрусталі), тас тұзының
кесектері тағы сол сияқты жеке ірі кристалдардың ғана кристалдық құрылысы
сыртынан тікелей көрініп тұрады. Мұндай жеке кристалдар монокристалдар деп
аталады. Ал қатты денелердің көпшілігінің құрылысы ұсақ кристалды, немесе
басқаша айтқанда, поликристалды болады. Тұздардың ұнтағы микроскопиялық
жеке кристалдардың жинағы болып табылыды. Бір тұздың ерітіндісінен осы
тұздың үлкенмонокристалын қолдан жасап шығаруға болады.
Металдардың барлығының да құрылысы поликристалды болады. Металдың жеке
ұсақ кристалдарын бірінің маңында бірін молекулалы күштер ұстап тұрады,
сонымен осындай ұсақ кристалдардың жалпы жиыны жай көзбен қарағанда бір
тұтас болып көрінетін кесек металл болып табылады. Кішкене жеке кристалдар
қалай болса солай ретсіз орналасатын болғандықтан металдың тұтас кесегінде,
оны құрайтын жеке кристалдар анизотропиялы болса да, анизотропиялық қасиет
болмайды.
Металлдың тегістелген, жылтыр бетін қарағанда оның поликристаллдық
құрылысын көруге болады; кейде металл кристаллының ірілігі соншалқты, оны
жай көзбен көруге болады, ал кейде оны тек микроскоптың жәрдемімен ғана
көруге болады.
Кейінгі кезде әр түрлі металдардың монокристалдарын шығарып алудың
әдістері табылады. Монокристалдар көбінесе балқыған затты суытқанда
құралады. Әдетте балқаған масса (зат) суығанда кристалданудың бірнеше
центрі (ядросы) құралады; осы центрлерде пайда болған кішкене кристалдар
кейін әр түрлі жылдамдықпен жан-жағына таралып көбейеді де, поликристалдық
құрылыс жасалады. Монокристалл шығарып алу үшін тек бір ғана ядро
өсерліктей жағдай туғызу керек. Балқыған затқа ұйытқы (жеке кристалл)
салу және ыдысты төменгі жағынан ақырындап суыту жолымен өлшемдері едәуір
болатын металл монокристаллды (мысалы, ұзындығы 20см және одан да артық
болатын стержень түрінде) шығарып алуға болады.
Бөлшектердің кристалдарда орналасуының 230 түрі бар екені көрсетелген.
Мұнымен қатар симметрия мен кристалдардың химиялық құрамының арасындағы
байланысы анықталған және кристаллдық-химиялық анализдің методы
сипатталған.
Кристаллдың сыртқы симетриясы – оны құрайтын болшектердің симметриялы
болып орналасуының нәтижесі. Бұл пікір XVIII ғасырдың аяқ кезінің өзінде-
ақ айтылған болатын. Кристалдардағы атомдар кеңестік решетка жасап біріне
қарағанда бірі симметриялы болып орналастындығына қазіргі уақытта біздің
тікілей дәлеліміз бар. Бұл дәлел рентген сәулелерінің кристалдық решеткадан
диффракциялана алатындығына негізделген.
Қатты денені құрайтын атомдар әрқайсысына көршілес атомдардың барлығы
да әсер етеді. Атомдар белгілі бір кеңістік решеткасының бұрыштарына
орналасқанда бұлардың әрқайсысына әсер ететін күштер бірін-бірі жояды да,
атом тепе-теңдік қалпында болады. Атомдар осылайша орналасуына олардың өз
ара потенциялық энергиясының ең аз шамасы сәйкес келеді де, тұтас
кристалдың беріктігі міне осыған байланысты болады.
Сонымен, кристалл беріктігі өзінің ішкі симметриясына байланысты
болатын күрделі архитектуралық құрылыс болып табылады.
Кристалды құрайтын атомдардың арасындағы өз ара әсер күштерінің сипаты
түрліше болады. Тұз кристалдарының атомдарында электр зарядтары болады,
олар иондар болып табылады. Оң иондар мен теріс иондар кристалл тұтасымен
алғанда нейтрал боларлықтай алмасып орналасады. Гетерполярлық деп аталатын
мұндай иондық решеткадағы бөлшектердің арасындағы өз ара әсер күштер болып
табылады.
Тас тұзының (NaCl) куб решеткасын көрсетуге болады (Сурет 1.1.4). Бұл
сияқты решетка ең қарапайым решетка болып табылады да, кубтық системаның
қатарына жатады. Натрий атомдары қара дөңгелекшелермен көрсетілген, олар оң
электр зарядымен зарядталған, яғни оң иондар болып табылады. Хлор атомдары
ақ дөңгелекшелермен көрсетілген, олар теріс электр зарядымен зарядталған,
яғни теріс иондар болып табылады.

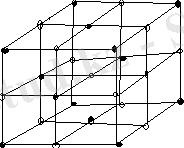
Сурет 1.1.4. Тас тұзының куб формалы решеткасы.

Күкіртті цинктің (ZnS) кеңістік решеткасы Сурет 1.1.5 көрсетілген.
Қара дөңгелекшелер цинктің оң иондаррын (Zn+), ақ дөңгелекшелер күкірттің
теріс иондарын (S-) кескіндейді. Күкіртті цинк решеткасының құрылысы тас
тұзы решеткасынң құрылысынан едәуір күрделірек.

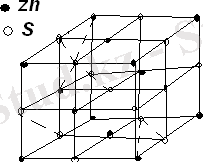
Сурет 1.1.5. Цинк жылтырының кеңістік решеткасы.

Химиялық жай қатты денелердің кеңістік решетка жасайтын атомдарының
барлығы нейтрал болады. Мұндай кристалдың решеткасы атомдык, немесе
гомеополярлық решетка деп аталады.
Атомдык решеткадағы өз ара әсер күштерінің табиғатын кванттық
механиканың негізінде ғана толық түсіндіруге болады.
Сурет 1.1.6 алмаздың кристалдық решеткасында атомдардың
қалай орналасатындығы көрсетелген.

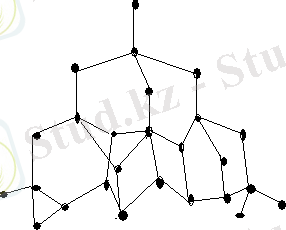
Сурет 1.1.6. Алмаздың кеңістік решеткасы.

Иондық (NaCl) және атомдық (алмаз сияқты) решеткалармен қатар
молекулалық решеткалар мен металл решеткаларын қарастыруға
келісілген, бірінші решеткалар көбінесе көп атомды химиялық қосылыстардың
(мысалы, Р2О5,5О3 т. с. с.) кристалдарына жатады; екінші решеткалар
электрді жақсы өткізетін жылтыр металдарға жатады. Металдардың
кристалдарын, тұрпайы түрде алғанда, ішінде бірінен-бірі белгілі бір
қашыктықта оң иондар орналасқан электрондық бұлт деп қарауға болады.
Кристалдық решеткада орнықты тепе-теңдіктің бар екендігін сығылу кезінде
кристалдарды құрайтын бөлшектердің арасында тебу күштерінің, ал созылу
кезінде тарту күштерінің пайда болатындығы көрсетеді. Мұны бөлшектердің
арасында тарту күштері қатарынан бар болу керек деп ұйғару арқылы
түсіндіруге болады; бұл күштердің бөлшектердің r аралығында тәуелділігі
түрліше болады. Тепе-теңдік жағдайында бұл күштер сан жағынан біріне-бірі
тең. R аралық азайғанда көршілес бөлшектердің арасындағы тебу күштері басым
бола бастайды ал бұл аралық артқанда тарту күштері басым болады.
Кристалдық решетканың Ер потенциялық энергиясын мынадай түрде
өрнектеуге болады:

(1.1.1)

бұл формуланың бірінші мүшесі тарту күштеріне, ал
екінші мүшесі тебу күштеріне сәйкес келеді. Сурет 1.1.7 решетканың
көршілес бөлшектерінің r аралықтарының өзгеруіне байланысты осы мүшелердің
әркайсысының жеке-жеке өзгерісі мен Е потенциялық энергияны кескіндейтін
жалпы қисықтын өзгерісі керсетілген. k2k1 болғанда r аралық кішірейген
сайын тебу күштері тарту күштерінен гөрі жылдамырақ артады, міне кристалдың
сығуға кері әсер ететіні осыдан болады. r= r0 мәніне потенциялық шұңқырдың
ең терең жері сәйкес келеді; r0 шама сыртқы күштердің әсері түспеген
кристалдағы бөлшектердің аралығын көрсетеді. Тепе-теңдік қалыптың маңында
бөлшектердің барлығы да, потенциялық шұнқырдың шегінен шықпай, аздап
тербеліп тұрады. Бөлшектердің тепе-теңдік қалыптың маңындағы осы
тербелістерінен кристалдағы жылулық қозғалыс туады.

Сурет 1.1.7. Кристалдық иондық решетканың Ер потенциялық энергиясы
иондарының r аралығына тәуелділігі.

Кристалдық решеткалар теориясын дамытқан Борн және бірқатар басқа
физиктер болды. Борн (1.1.1) формуладағы k1 және k2 дәреже көрсеткіштері
белгілі болса, кристалдардың серпімділік қасиеттерін, кристалдың жасалу
энергиясын, оның оптикалық қасиеттерін тағы басқаларды есептеп шығаруға
болатындығын көрсетті. Тәжірибемен үйлестіру үшін гетерополярлық
решеткаларда к=1 және к=9 деп алу керек; гемеополярлық решеткаларда к2
көрсеткіштің мәні үлкен болады.
NаСІ сияқты заттардың куб формалы қарапайым кристалдық решеткасының
энергиясын схема түрінде былай есептеп шығаруға болады.
е және +е зарядтары бар және бірінен-бірі г0 аралықта тұрған
оңашаланған екі ионның потенциялық энергиясы мынаған тең:
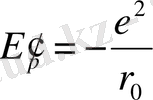(1.1.2)
Решетканың ішіндегі екі ионның потенциялық энергиясы мынадай екі
себеппен бұл шамадан артық болады: 1) иондардың әрқайсысына оған көрші
тұрған ион ғана емес, решетканың басқа иондары да әсер етеді; 2) иондар,
біріне-бірі әсер ете отырып, бірін-бірі поляризациялайды, ал мұның өзі тебу
күштерін туғызады. Есептеулер NаСІ сияқты кристалл үшін (1.1.2)
формуланың орнына мынадай формуланы алуға болады:

(1.1.2а)

(1.1.2а) формуламен өрнектелген потенциялык энергия сан жағынан көршілес
екі ионды решеткадан жұлып алып оларды шексіз алысқа ұзатып апару үшін
істелетін жұмысқа тең, екінші сөзбен айтқанда, ол - решеткадағы көршілес
екі ионның арасындағы байланысты үзуге кететін жұмысқа тең. Решетка затының
бір грамм - молекуласында N пар (қос) ион бар және куб формалы 1
решеткадағы әрбір ионның 6 көршілес ионы бар, сонымен, бір грамм-
молекуланың құрамына кіретін барлық иондарды бірінен-бірін шексіз
қашықтыққа бытыратып әкету үшін 6N байланысты үзу керек болады. Бұдан
решектканың бір грамм-молекулаға қатысты алынған. Ең толық потенциялық
энергия 6NЕр көбейтіндісіне, яғни мынаған тең болады:

(1.1.3)

Куб решеткадағы көршілес иондардың r0 аралығын былайша анықтаймыз:
егер ρ- қарастырылып отырған кристалдың тығыздығы, μ- молекулалық салмақ,
ал V0 — бір грамм-молекуланың көлемі болса, онда

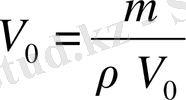
Элементарлық бір куб ұяға келетін υ = г03 көлемді табу үшін V0
көлемді грамм-молекуладағы ұялардың, ондағы (бір грамм-молекуладағы)
иондардың санымен бірдей болатын санына, яғни 2 N-гt, бөлеміз:

бұдан (1.1.4)

r0 аралықтын бұл мәнін потенциялық энергияның (1.1.3) формуласына
қойсақ, мынау шығады:

(1.1.5)

е мен N тұрақты шамалар болатындықтан, кейінгі өрнекті мына түрде көшіріп
жазуга болады:

(1.1.5а)

Егер ρ тығыздықты гсм3-мен, μ молекулалық салмақты бір грамм-
молекуладағы грамм санымен, ал Ер потенциялык. энергияны бір грамм-
молекулаға келетін калория санымен өрнектесек, онда тұрақты шама К-ның сан
мәні 545 болады. СsСІ сияқты заттардың кристалдық решеткасына арналған
формулалар (1.1.5а) формулаға ұқсас; бұлардың (1.1.5а) формуладан
айырмашылығы тек К тұрақтысының сан мәнінде ғана болады. Борнның
есептеулерін тікелей тәжірибе жасап тексеру қиын, өйткені қатты кристалды
еркін иондардың жиынына айналдыру мүмкін емес. Бұл есептеудің дұрыстығын
бірнеше тәсілмен жанамалап тексеруге болады.
Мысалы, NаСІ мен KJ тұздарының КСІ мен NaJ тұздарына айналу реакциясын
қарастырайық:

NаС1(кат) +КJ(қат) = NаJ(кат)КС1(кат)
Бұлардағы (кат) деген индекстер химиялык, символдар тиісті заттардын
катты кристалдық фазасына жататындығын көрсетеді ΔU айналу энергиясы
мынаған тең болатындығы өзінен-өзі түсінікті:
ΔU =-[Eр(NаС1)+Eр(КJ)] + [Eр(NаJ)+Eр(КС1)];
Олай болса (1.1.5а) формула бойынша NаСІ, ҚJ тағы сол сияқты
заттардың кристалдық решеткаларының Ер (NаСІ), Ер (ҚJ) тағы сол сияқты
потенциялық энергиялары арқылы К тұрақтысының мәнін есептеп шығаруға
болады. Екінші жағынан, жуықтап алғанда, ерітінділер олардағы молекулалар
тегіс диссоциацияланатындай әлсіз етіліп алынған жағдайда ΔU айналу
энергиясы тұздардың q еру жылуларының айырмасына тең болады:
ΔU = (q = [q(NаС1)+q(КJ)]- [q(NаJ) +q(КС1)].

Кесте 1.1.1
Бірнеше тұздардын еру жылуы арқылы табылған (U және (q мәндері

Реакция ΔU ∑q
КСІ + LіВг =КВг+LiС1 +4 +3,6
КСІ + NаВг =КJ + LіС1 +7 +7,2
КС1 + NаВг = ҚВг+NаС1 +3 +2,0
КСІ + NаJ =КJ + NаС1 +5 +3,4

Егер эксперимент жасауда ∑q аз ғана дәлдікпен анықталатындығын (үлкен
шамалардың айырмасы аз болатындықтан) еске алатын болсақ, онда ∑q мен
ΔUшамалар біріне-бірі ойдағыдай дәл келеді деп есептеуге болады. Тексерудің
екініші тәсілі Борн - Габердің дөңгелектік процесі деп аталатын
процесті қарастыруға келіп тіреледі. NаСІ алынған жағдайда бұл процесс
мынадай схема түрінде орындалады:
Nа+ Nа(қат) Nа(қат)
NаСІ(қат) Nа
С1(қат)
СІ - СІ(қат) СІ2(қат)

Біз әуелі қатты кристалл NаСІ -дың бір грамм-молекуласы бос Nа+ және
СІ — ионларлың жиынына ажырайды деп есептейміз; бұган сан жағынан алғанда
решетканын Еp потенциялық энергиясына тең жұмыс жұмсалады. Сонан кейін Nа+
және СІ ион газдар нейтрал атом газдарына, ягни Nа (газ) мен СІ (газ)
газдарына айналады. Бұған сан жағынан бір грамм-молекулаға қатысты алынған
Аj(Nа) және Аj (СІ) иондалу жұмыстарына тең жұмыс жұмсалады. Әрі карай газ
Nа(газ) қатты металл натрийға айналады [L(Nа) буға айналу жылуына тең жұмыс
жұмсалады], ал атомдық газ С1 (газ) кәдуелгі екі атомды газ тәрізді хлордың
(СІ2) грамм-молекуласының жартысына айналады (диссоциациялану q(Сl)
жылуына тең жұмыс жұмсалады). Ақырында, химиялық реакция жолымен қатты
металл натрий мен газ тәрізді хлордан NаСІ-дың катты кристалының бір грамм-
молекуласы жасалады: мұнда Q(NаСl) түзілу жылуы бөлініп шығады. Дөңгелек
процесте барлык жұмыс пен алынған және берілген барлық жылу мөлшерлерінің
(эквивалентті жұмысқа шаққандағы) косындысы нольге тең болады. Сондықтан
мынау шығады:

Осы теңдіктің оң жағындағы шамалардың әркайсысын өлшеп, Ер эпергияның мәнін
табуға болады. Анығында тікелей эксперимент жолымен осы шамалардың теріс
ионның (СІ-) жасалуына кететін жұмыстан басқаларының, барлығын да анықтауға
болады. Жобалап алғанда Аj(С1) шама 90 калмоль деп есептеуге болады. Сонда
тәжірибеден мәлім (Аj(Nа) = 117 кал, L(Na)=27 kал, 12 q(С1)=29 kaл,
Q(NаСІ) =98 кал мәндерді пайдаланып, NаСІ решеткасының энергиясы, шамамен,
180 калмоль тең шама екендігін табамыз. Егер (1.1.5а) формулаға тас тұзы
грамм-молекуласының μ = 58,5 гмоль массасын және оның р =2,16гсм3
тығыздығын койсақ, онда Еp = — 182 калмоль болып шығады.
Кристалдық решеткалардың неғұрлым дәл теориясы (әсіресе олардың
төменгі температуралардағы күйін білгісі келстін теория) кванттык
механикаға негізделуге тиіс екендігі есте болу керек.

1.2. Қатты денелердің серпімді деформациясы

Қатты денелердің барлығы да сыртқы күштердің әсерінен
деформацияланады, яғни өзінің формасын өзгертеді. Сыртқы күштің әсері
тоқталғаннан кейін жоғалып кететін деформация серпімді деформация деп
аталады. Мысалы, созылған пружина созушы күштің әсері тоқталғанан кейін
өзінің бұрынғы қалпына келеді. Күштің таңбасы өзгергенде серпімді
деформацияның таңбасы да өзгереді, мысалы пружина созушы күштің әсерінен
ұзаратып болса, сығушы күштің әсерінен қысқарады. Гуктың тағайындаган заңы
бойынша деформацияның Δх шамасы әсер етуші f күшке пропорционал
болады:
Δх =Kf (1.2.1)
мұндағы К — алынған қатты дененің осы деформациясы үшін тұрақты шама.
Бойлық созылу немесе бір жақты сығылу деформациясы деп
аталатын қарапайым деформацияны қарастырайық. Ұзынды L, көлденең
қимасы S бір текті стерженьнің. ұштарына fп- күш түсірілген болсын; осының
салдарынан стерженьнің ұзындығы ΔL шамасына өзгереді. Созушы күштерді
оң күштер деп есептейміз; бұл жағдайда (Сурет 1.2.1а) ΔL шама да оң
шама болады, яғни стержень созылады. Сығатын күштерді теріс күштер деп
есептейміз; бұл жағдайда (Сурет 1.2.1б) ΔL шама да теріс шама болады; бұл —
стерженьге бір жақты сығу күші түскенде оның L ұзындығы кысқарады дегенді
көрсетеді.

Сурет 1.2.1. Созылу деформациясы (а) мен сығылу деформациясы (б).

Деформацияны сипаттау үшін стерженьнің ΔL абсолют ұзаруының мәні емес,
оның ΔLL салыстырмалы ұзаруының мәні алынады. Бұлай етудің себебі бірдей
материалдан жасалған және көлденең қималары бірдей, бірақ біреуінің
ұзындығы 2 см, ал екіншісінікі 10 м екі стерженьді ΔL .= 1 см ұзарту ісі
бірдей болмайтындығынан екендігі өзінен-өзі түсінікті. Бүл сиякты
стерженьдерді бұрынғы ұзындықтарының бірдей үлестеріне (мысалы,
үлестеріне) созып ұзарту үшін екеуіне де бірдей f күш жұмсау керек
болады. Сонымен, деформацияны үзындықтың ΔL L салыстырмалы өзгеруімен
сипаттау керек. S көлденен қималары әр түрлі стерженьдерге бірдей күш
түскенде стерженьдер неғұрлым жуан болса, яғни s неғұрлым үлкен болса, ΔL
L салыстырмалы деформация солғұрлым аз болады. Бұдан созылудың (сығылудың)
серпімді деформациясы үшін ұзындықтың ΔL L салыстырмалы өзгеруі fnS
шамасына яғни стерженьнің көлденең кимсының бірлігіне түсетін күшке,
пропрционал болу керек екендігі шығады. Осы S шама кернеу деп
атайтамыз. Сонымен, нәтижеде мынау шығады:

, немесе (1.2.2)

мұндағы серпінділік коэффициенті деп аталатын а стерженьнің жасалған
материалына ғана байланысты болады. ά серпімділік коэффициентімен қатар
материалды осы коэфициенттің кері шамасымен сипаттауга келісілген:
(1.2.3)
Бұл шама серпімділік модулі немесе Юнг модулі деп аталады. 2) теңдіктегі ά
коэффициенттің орнына Юнг модулін қойсақ, мынау шығады:

(1.2.2а)

(1.2.2) және (1.2.2а) формулалардан мыналарды анықтаймыз:
(1.2.4)
бұдан мынадай қорытынды шығады: а серпімділік коэффициенті сан жағынан
ұзындықтың бір кернеу бірлігінің әсерінен болатын ΔLL салыстырмалы
өзгерісіне тең; Юнг модулі сан жағынан ұзындыктың бірге (бір бүтінге) тең
салыстырмалы езгерісін туғызатын рп кернеуге тең.
Салыстырмалы ұзару бір бүтінге тең болғанда ΔL = L болады. Бұдан Юнг
модулі сан жағынан стерженьді екі есе ұзартатын рn кернеуге тең деген
қорытынды шығады. Шынында материалдардың басым көпшілігі екі есе ұзаруға
жетпей-ақ үзіліп қалады, сондықтан стерженьге іс жүзінде сан жағынан Юнг
модуліне тең рn кернеу түсіруге болмайды. Бастапқы ұзындығы L0 болатын
стерженьге рп кернеу түсірілген болсын, сонда стерженьнің жаңа ұзындығы
мынадай болады:

L=L0+ΔL
(1.2.3) формула бойынша
ΔL=άL0pn
болғандықтан стерженьнің жаңа ұзындығы L мынаған тең болады.
L=L0(1+άpn) (1.2.5)
Бұл формуладан серпімді деформация шегінде стерженьнің ұзындығы
кернеуге пропорционал түрде өзгеретіндігі көрінді.Стержень созылғанда
немесе сығылғанда сыртқы күштер жұмыс істейді. (1.2.2а) формуладан
стерженьге түсетін күш әрбір уақыт кезеңінде мынаған тең болатындығын
көреміз:

яғни деформация кезінде күш тұрақты болып қалмайды, стержень ұзындығының ΔL
өзгерісіне пропорционал болып өзгеріп тұрады. Осындай айнымалы күштің
жұмысын анықтаған едік. Мүны осы жерде басқа тәсілмен есептеп шығарайық.
Стерженьнің ұзындығы L мәнінен L + ΔL мәніне дейін өзгеретін болсын, сонда
А жұмыс мынаған тең болады:

А= ƒn ΔL
мұндағы ƒn —күштің орташа мәні. ƒn күш ΔL ұзаруға пропорционал болып
артатындықтан, күштің бұл орташа мәні ΔL = 0 болған кездегі күштің ƒn = 0
мәні мен ұзару ΔL болғандағы ƒn =ESL ΔL мәнінің арифметикалық орташа
мәніне тең болады, яғни
, бұдан
Бұл жұмыс серпімді деформацияланған стерженьнің потенциялық энергиясын
жасауға жұмсалады:

Сонымен, серпімді деформацияланған стерженьнің потенциялық энергиясы
деформацияның квадратына (ΔL2) пропорционал болады екен.
Стерженьнің созылу немесе сығылу деформациясында оның, кесе бетінің
өлшемдері өзгереді. Созылғанда стерженьнің көлденең қимасы кішірейеді, ал
сығылғанда оның көлденең қимасы үлікейеді. Стержень жуандығының Δdd
салыстырмалы өзгеруі әсер ететін рn кернеуге пропорционал:

(1.2.7)
β коэффициенті бойлық созылудың көлденеңдік сығылу коэффициенті деп
аталады.

қатынасы Пуассон коэффициенті деп аталады. Пуассон коэффициентінің өрнегін
пайдаланып (1.2.7) формуланы мына түрде өзгертіп жазуға болады:

(1.2.7а)

Бір текті изотроптык, денелердің (және металдардың) көпшілігі үшін
σ Пуассон коэффициенті сан мәні жағынан ¼-ге
жуық болады.
Ығысу деформациясы дсп аталатын тағы бір жай деформацияны
қарастырайық. Ығысу деформациясы ft күшінің өзінің түсетін бетіне жанама
бағытпен әсер етуінен болады (Сурет 1.2.2). Осындай күштің әсерінен дененің
қабаттары біріне қарағанда бірі ығысады да, күш түсетін бетке
перпендикуляр физикалық аЬ тузуі (яғни қатты дененің белгілі бір
бөлшектерімен байланысты түзу) бір ψ бұрышқа бұрылады.

Сурет 1.2.2. Ығысу деформациясы.

Ψ ығысу бүрышы кішкене болғанда оны шамамен мынаған тең деп айтуға болады:

мұндағы аb = d — дененің қалыңдығы, bb' — жоғарғы қабаттың астынғы қабатқа
қарағанда ығысуының абсолют шамасы. Бұдан ығысу бұрышы ψ салыстырмалы
ығысуды сипаттайтындығын көреміз, сондықтан Гук заңының қолданылу шегінде
мынаны жазуға болады:

(1.2.8)

мұндағы п — ыгысу коэффиңиенті деп аталатын және тек білеудің жасалған
материалына ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.