Есептердің берілуі

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 15 бет
Таңдаулыға:

М а з м ұ н ы

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...

3
І-тарау. Сызықтық бағдарламалау есептері
... ... ... ... ... ... ... ... .. ... ... .
1.1. Сызықтық бағдарламалау есептерінің берілуінің негізгі 4
түсінігі ... ... ... ..
1.2. Сызықтық бағдарламалау есебнің жалпы берілуі ... ... ... ... ... ... ... ..5

ІІ-тарау. Жүкті тасымалдау тиімді есебі
... ... ... ... ... ... ... ... .. ... ... ... .
2.1. Бастапқы жоспарды анықтаудағы солтүстік - батыс бұрыш
әдісінің алгоритмі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 11
2.2. Бастапқы жоспарды анықтаудағы ең кіші нарық әдісінің 15
алгоритмі ... ..
Қорытынды ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 16
Пайдаланылған әдебиеттер

Кіріспе

Экономика-математикалық модельдің өңделу және орындалу процесі бірнеше
кезеңдерден тұрады:
● Есептердің берілуі;
● Модельдердің орындалуы;
● Модельдерді шешудің алгоритмі немесе математикалық әдістерін талдау;
● ЭЕМ-де есептерді шешу және шешімдердің нәтижесінің экономикалық
интерпретациясы.
Есептің берілгеніне ерекше мән беру керек және бірінші орынды
модельдің мақсатының шартына қарау қажет, жауапты тапсырушы және жүйенің
модернизациясы және модельді орындаушы арасында толық түсінушілік болуы
керек. Барлық келесі кезеңдердегі модельдеудің белгілі бір анықталған
бағытта модельдік мақсаттың нақты орындалуын анықтайды. Модельдің мақсатын
дұрыс тұжырымдау метажүйенің анализінің нәтижесінде жүзеге асырылады,
мұндағы зерттелуші жүйе элемент ретінде қарастырылады немесе басқа сөзбен
айтқанда, анализдің нәтижесінде жүйе мен сыртқы ортаның бір-біріне әсері
байқалады. Есептің берілуін объектіні өте жақсы білетін және орындай алатын
арнайы маман жүзеге асыру қажет.
Экономика-математикалық модельдерді орналастыру және орындау есептің
берілуі және модельдердің неғұрлым нәтижелі орындалу шартымен толығымен
сәйкес келуі қажет.
Математикалық модельдерді орындау жүйені жеткілікті түрде терең
біліп, модельдің ішіне тек қана кіруді үйренбей, модельдің ішіндегі
нәтижелі емес нәтижелерді алып тастап отыру (модельді жеңілдету мақсатында)
қажет.
Математикалық модельді құрастырудың негізгі мақсаты жай модель мен
оған сәйкес зерттелетін жүйедегі мәндесін табу. Алайда, математикалық
моделді талдаудың процесі ешқашан да толық тұжырымдалмайды. Сондықтан да
модельді талқылаушы модельден сол немесе басқа элементті алып тастау
шешімін қабылдап, жүйені өзінің білімімен басқарып, осыған ұқсас
модельдерді талдау нәтижесін пайдаланып отыруы қажет. Сондықтан да
модельдеуді тек қана ғылым емес, өнер деп те атайды.
Берілген кезеңді жүзеге асыру үшін жеткілікті түрде жақсы
математикалық әдістер жайлы білім және математика ғана жүзеге асырады.
Модельдерді тұжырымдауды өте жақсы жүзеге асырушы экономистер болып
саналады, себебі олар қазіргі математикалық аппараттарды сенімді қолдана
алады.
Модельді шешудің алгоритмін немесе математикалық әдісін жасау өзінше
күрделі және қиын көлемді кезең, себебі берілген математикалық әдістер
немесе алгоритмдердің көмегімен модельдер шешімін табу мүмкін емес
жағдайлар да кездеседі.
Модельдің шешімінің нәтижесінің экономикалық интерпретациясы
экономикалық жүйелердің экономика-математикалық модельдеуінің өте жауапты
кезеңі болып табылады.
Тиімді жоспарды табу нақты, ыңғайлы жоспармен жұмыс жасау болып
табылады. Тиімді жоспарды қажетті нақтылық деңгейге жеткізу процесінде
функционалдық объектілер жағдайында оның жан-жақты экономикалық анализінің
нәтижесі шешуші рөл ойнайды.
Осындай анализдеу процесінде біріншіден, қарастырылушы варианттар
шешімінің қалыптаспаған модельдегі факторымен сәйкесі, екіншіден, жаңа
басқарушы параметрлердің мәндерін таңдау, егер талдайтын вариант жоспары
қанағаттанарлықсыз болса. Расында, бұл кезеңнің өзі таза шығармаылық
процесс болып табылады, ең алдымен ол адамның біліміне сүйенеді, тәжірибесі
және интуициясына басқару шешімін меңгере алады.

I-тарау. Сызықтық бағдарламалау есептері

1.1. Сызықтық бағдарламалау есептерінің берілуінің негізгі түсінігі

Экономикадағы тиімді есептер мекемедегі жоспарлардың салалық немесе
халықтық шаруашылықта қысқа, орта немесе ұзақ мерзімді уақыт аралығында
жасалуына сәйкес туындайды.
Мекемеге байланысты өндірістің тиімді есептері максимальды айлық
немесе пайда формасында берілген шығарылатын өнімдер түрлері және қалған
ресурстарды шектеумен түрленеді. Есептер өндірістің бірнеше әдіспен
берілген өнімнің көлемдеріне жіберілетін минимальды шығын формасы түрінде
де беріледі. Тиімді есептер текқана өндірістің нақты сектор экономикасында
емес, сонымен қатар саудада, банкілік және сақтану жағдайларында да
қойылады.
Сызықтық бағдарламалаудың дербес жағдайларына берілетін есептерді
мысалмен келтіруге болады.
Фабрика айлық өндірістік бағдарламасында ресурстың үш түрін иеленді:
жұмысшылар күші (800 адамкүн), құрал-сайман(1400 станоксағ), шикізат
(4080 т) және төрт түрлі өнім шығара алады, олардың тарату бағасы белгілі.
Өндірістен шығатын ресурстардың мөлшері берілген, әрбір түрдің бірлік
өнімі. Барлық мағұлмат 2.1 кестесінде жазылған.

Кесте 1.1.1
Ресурстар Шығатын ресурстар нормасы бірлік өніммен Нақты
ресурстар,
т

Продукция Продукция Продукция Продукция 4
1 2 3
Еңбек, 7 2 2 6 800
адамкүн
Шикізат, т 5 8 4 3 4800
Құрал-сайман,2 4 1 8 1400
станоксағ
Бағасы мың 3 4 10 5
сом

Өнімнің өндірістік жоспарын табу және оны шығарғандағы жалпы бағасы
ең жоғары болуы қажет. Келтірілген тұжырым есептің экономикалық берілуі деп
аталады. Есептің экономика-математикалық модельінің есебі келесі түрде
болады:

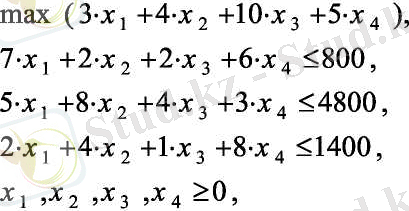
мұндағы X= (x1, x2, x3, x4)T - өндірістегі өнімнің әр түрінің көлемінің
векторы. (1.1.1) есебі сызықтық бағдарламалау есебідеп аталады.

1.2. Сызықтық бағдарламалау есебнің жалпы берілуі

Сызықтық бағдарламалаудың есебі жалпы түрде берілгенде үш түрлі
формада беріледі: еркін, симметриялық және конондық.
СПЕ-нің еркін формадағы түрі

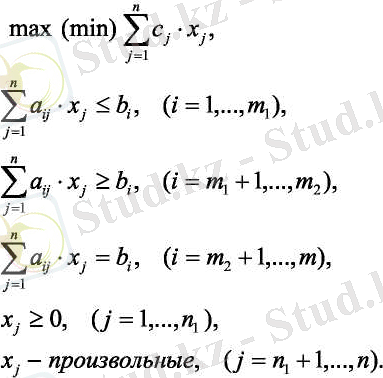
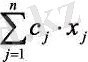
Берілген өрнек мақсатты функциялық (немесе критерийлік) есеп.
(Х1, Х2 ,..., Хn) – есептегі айнымалылар (1.2.1) есебіндегі теңсіздіктер
жүйесі D есебінің мүмкін болатын мәндер (жоспарлар) облысын анықтайды және
дөңеүс көпжақты формалы болып келеді. (1.2.1) есебіндегі тшеңдік және
теңсіздіктер шектелген деп аталады.
Әрбір теңсіздік жарты кеңістікті анықтайды, ал теңдік – кеңістіктегі
айнымалылар (Х1, Х2 ,..., Хn) жазықтығы (1.2.1) есебінің шешімі тиімді шешім
(немесе тиімді жоспар) деп аталады және
Х* = (Х*1, Х*2, ..., Х*n) арқылы белгіленеді. Тиімді шешімдер D
облысыныңшекарасында жатады.
Егер D облысы шектелген болса, онда СП есебінің жалғыз немесе шексіз көп
шешімдері болады. Егер жалғыз шешімі болса, онда ол D көпжағының бір
төбесімен беттеседі.
Егер мақсатты функцияның градиенті c = (с1, c2 ... ., сn) шектеудің
біреуінің градиентімен коллиниар болса, онда есептің шексіз көп шешімі
болады, ол шешімдер берілген шекарада жатады.
Егер шектеулер тәуелсіз болса немесе мақсатты функциялар шектелмеген
болса, онда (1.2.1) есебінің шешімі болмайды.
Егер D облысы шектелмеген болса, онда шешімі табылуы мүмкін,
шектелмеуі де мүмкін.
Кез-келген минимумға берілген есеп максимумға берілген есепке
келтірілуі мүмкін және керісінше мақсатты функцияны –1-ге көбейту керек.
Есепті ңоптимальды жоспары бұдан өзгермейді, ал мақсатты функцияның мәнінің
таңбасы өзгереді. Шешіп болған соң қайтадан мақсатты функцияның таңбасын
өзгерту керек.
СПЕ-нің максимумға берілген симметриялық формасы төмендегідей түрде
болады:

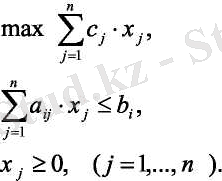
Есептің минимумға берілген симметриялық формасы төмендегідей:

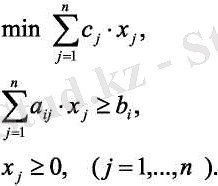
Егер барлық bi ≥ 0 болса, онда (1.2.3) есебі келесі эконеомикалық
мағынаны білдіреді: xj − j-шітүрдегі ө-нүімнің өндірістегі көлемі, cj −
бағасы немесе бірлік өнімнің пайдасы, аij – i-ші түрдегі ресурсты тарату
нормативінің j-ші түрдегі өнімінің өндірістегі бірлігі, bi − i-ші түрдегі
ресурстар запасы.
Өнімнің Х* = (Х*1, Х*2, ..., Х*n) өндірістегі жоспарын анықтау керек, ол
берілген шектеулі ресурстардың максимальды табысын немесе пайдасын береді.
Тиімді жоспардағы қол жеткен теңдік шектеуі дифицит ресурстарымен
сәйкес келеді, қалған ресурстар дифицит емес деп аталады.
СПЕ конондық формасы төменде көрсетілген:

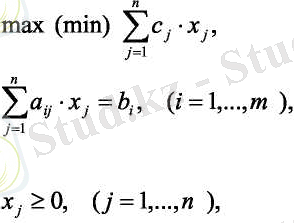
Сызықтық алгебрадан белгілі, сызықтық белгісіз теңдеулер саны
айнымалылар санынан артық болуы мүмкін емес. Сондықтан (1.2.4)-те n≥m деп
есептеуге болады.
Анықтама: Егер (1.2.4) есебінің коэффициенті 1-ге тең айнымалы болып,
ал басқа шектеуде жоқ болса, онда ол базистік деп аталады да, ал басқа
шектеулі айнымалыларды бос деп атайды.
Егер базистік айнымалы барлық шектеуде бар болса, онда СПЕ мұндай
формасын базистік айнымалысы бар конондық форма деп атайды. Базистік
айнымалысы бар конондық формасимплекстік алгоритмдік есептерді шешудің
бастамасы деп аталады.
(1.2.4) шартшын қанағаттандыратын кез келген векторды (Х1, Х2 ,..., Хn)
және m-нен аспайтын нөлдік емес компоненті бар тірек жоспары деп атайды.
Егер конондық формадағы барлық bi ≥ 0 болса, онда (1.2.4) есебінің
тірек жоспары болады, мұндағы базистік айнымалылар bi –ге тең, ал басқа
(бос) айнымалылар нөлге тең. Мұндай жоспар бастапқы тірек жоспары деп
аталады.
Айнымалы базистік деп аталады, егер теңсіздіктің сол жағынан қосылып
немесе азайтылып отырса, теңдөік алу үшін (1.2.2), (1.2.3) есептерінде
баланстық айнымалылар базистік болып табылады.
Келесі түрлендірулердің нәтижесінде кез келген СПЕ формасы конондық
формаға келтіріледі:
● айнымалы енгізу, егер кез келген мәндерді қабылдайтын екі жаңа оң
айнымалылардың айырмасы;
● баланстық айнымалы енгізу.
Егер СПЕ конондық формадағы шектеуде базистік айнымалы жоқ болса,
онда жасанды айнымалы енгізіледі. Бұл жағдайда мақсатты функция жасанды
айнымалы мен максимумға берілген есептегі М коэффициентінің айырмасы және
минимумға берілген есеп осындай жолдың қосындысына байланысты өзгереді. М
коэффициенті үлкен оң сан болып табылады.
Жасанды айнымалы енгізу және мақсатты функцияның өзгерген есебіндегі
корректировкасы М-есеп деп аталады.
Мысалы СП есебі төмендегідей түрде болсын:

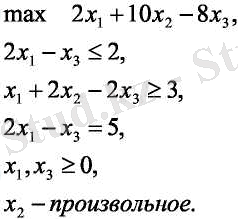
Конондық формаға келтіру үшін x2=x12−x22 алмастыруын жасаймыз, ал
теңсіздікке x4,x5 баланстық айнымалы енгіземіз және x6 жасанды айнымалы
енгіземіз. Сонда М есеп (1.2.5) үшін төменднгідей түрге келеді:

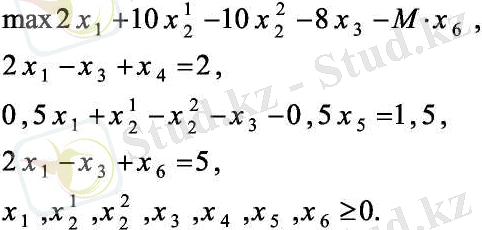
Кез келген экономикалық жүйе, салыстырмалы түрде алғанда масштабы
кішісін алсақ та, жоғарыда белгіленгендей, күрделі жүйе болып табылады.
Онда сыртқы жағдайлар әсерінен өзгеріп тұратын біраз техникалық
экономикалық және социалдық процесстер қарым-қатынас жасайды. Осы
жағдайларда экономикалық жүйелерді басқару қиындық туғызады. Бұл қиындықты
шешу, жүйелілік талқылау ғылыми аппаратты қолдануды талап етеді. Осының
эффектілік тәсілдерінің бірі экономикалық жүйелердің экономика-
математикалық модельдеуі болып табылады.
Жалпы жағдайда, басқа бір объектілердің (оның моделінің) арқасында
екінші бір объектінің (оригиналының) қасиеттерін көрсетіп шығаруын
модельдеу деп түсіндіреді.
Әдебиетте экономика-математикалық модельдеудің қалыптасқан анықтамасы
жоқ, анықтаманың жалпы көлемдік формулировкасының күрделілігін атап өтіп,
әрі қарай экономикалық моделдеп, бір-бірімен байланысты математикалық
тәуелділіктердің жиынтығы деп түсінеміз. Бұлар теңдеу немесе теңсіздік,
әйтеуір нақты экономикалық объектілердің жұмыс атқару шарттарын көрсету.
Басқа сөзбен айтқанда, экономика-математикалық модель – бұл зерттеліп
жатқан экономикалық объектінің (процесстің) математикалық айнасы. Осының
көмегімен жұмыс атқарылуы оқылып, оның сыртқы ортаның мінездемесі өзгерген
жағдайларда нәтиженің өзгеруі бағаланады.
Көрсетілген тәуелділіктер қарым-қатынасы әйтеуір бір деңгейде
айнымалы модель деп аталатын жиындар арқылы жүзеге асырылады. Сонымен қатар
экзогендік, яғни сырттан тыс модель ауыспалы және ауыспалы эндогендікті
ажыратады.
Бұлардың өзгеру траекториялары модельдің (өтілуінің) шығарылуының
қорытындысы арқылы анықталады. Практикалық зерттеулердегі экономика-
математикалық модельдеуді пайдалану негізі эндогендік ауыспалы тәртібінің
болжамында анықталады. Онда да экзогендік тәртібінің бір жағдайлардағы
келісімімен (әйтсе де, экзогендік ауыспалы тәртібі туралы келісімді басқа
да экономика-математикалық модельдер арқылы анықтауға болады).
Экономика-математикалық модельдеудің талай рет өткізілуі осы
процессте экономика-математикалық модельдеу деп аталады. Сонымен экономика-
математикалық модельдеу деп, біз әрі қарай қазіргі есептеуіш техника
базасында экономика-математикалық құрастыруды және оқуды танитын боламыз,
ол зерттеліп жатқан экономикалық объектіні (процесті) ауыстыра алуы тиіс.
Модельді қолданып басқару процесін бұл жағдайда нақты экономикалық
жүйенің тәртібін талдау үшін тиімді шешімін табу тәсілі деп жүйемен
ешқандай тәжірибе жасамай қарауға болады. Мұның сызбасын төмендегідей түрде
көрсетуге болады (1.1 сурет).

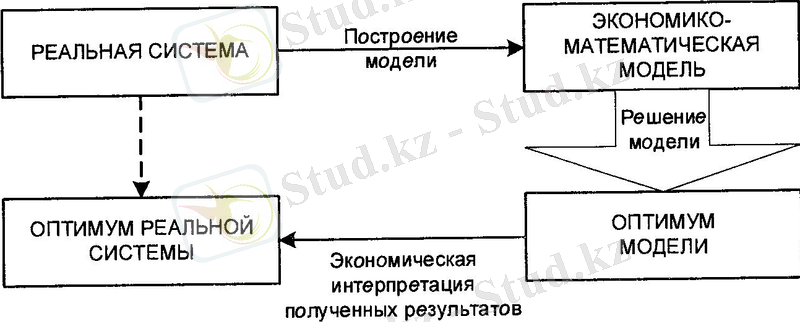
Сурет 1. Модельдеу принципін қолдану сызбасы.

Сурет1-де көрсетілгендей шешуге апаратын тікелей жол айналмалыға
алмастырылады, ол өзіне сәйкес модельдің тиімділігін және құрылымын қосады.
Сонымен, экономика-математикалық модельдеу тәсілін қолдану, бізге
ақиқатты қателер жасау және тексеріп көру тәсілін қолданбай-ақ экономикалық
жү.йелерді басқаруды ұсынады. Экономика-математикалық модельдеу – ғылыми
болжамдау және талқылаудың нақты фундаменті. Объектімен емес, модельдеумен
жұмыс істеу, толық және көрнекі ақпараттың, уақытылы және жылдам алынуына
жағдай туғызып, оның ішкі байланысының сапасы мен сандық параметрлерін
ашады.
Модельде сандар зерттеулері арқылы әртүрлі жағдайда нақты
экономикалық жүйелердің жұмыс істеуі жайлы толық ойға алсақ, экономика-
математикалық модельдер тек қана басқару мақсатындағы құрылымға емес,
модельдеу жүйесінің даму процесінің терең талдануына да үлкен нәтиже
береді. Расында, модельді туындағанда, зерттеуші амалсыз модельденіп жатқан
жүйені танып біледі, оны оқу объекті ретінде айнала ортадан бөлектейді,
сөйтіп оған қойылған мақсаттарына және бар мүмкіншіліктеріне (ресурстарына)
сәйкес оның ақпараттық, сонан соң әйтеуір бейнелеуін қарастырады.
Әрі қарай модель тәртібі арқылы ол жүйені талдайды, оның қасиетін,
жағдайын, мүмкін боатын, рұқсат берілген және тиым салынған өмір сүру
қалпын т.б оқиды.
Экономика-математикалық модельдеу принципін қолданғанда, материалдық
және еңбек шығындары біраз азаюы мүмкін, бұл тәжірибелік ыңғайға лайық,
олар керек ақпараттың кіші өлшемін ғана береді. Есепатеуіш модель
тәжірибесі ешқандай шектеуліктерге бағынбайды, математикалық модель кез
келген қауіпсіз базада және ойда жоқ жағдайларда сынақталуы мүмкін.
Экономика-математикалық модельдеудің ерекше ролі – жоғары нәтижеде
есептеуіш технниканы қолданудағы күрделі жағдайын, экономикалық жүйелердің
жұмыс атқаруын және оларды басқаруын шешуде. Есептеуіш техника көмегімен
кез келген есепті шығару, ол қатаң қалыптасудың керектігі. Өкінішке орай,
экономика-математикалық процесстер (мысалы, техникалықтарға қарағанда) өте
әлсіз қалыптасқан. Қалыптасқан экономикалық білімнің көбеюі қазіргі уақытта
есептеуіш техника процессінен өте қалып қойған. Бұны бағдарламалық
қамтамасыз құнынан айқындауға болады, өйткені ол техника құнынан біраз
жоғары. Нақты есептердің шешу сапасы бұл жағдайларда тек қана есептеуіш
техниканың мүмкіншілігімен емес, сәйкестендірілген математикалық
модельдердің жетілмегендігінен. Есептеуіш техника тек қорытындыны шығаруды
тездетеді, ал сонымен сәйкес экономика-математикалық модельдердің сапасына
байланысты дұрыс боуы да, қате шығуы да мүмкін, осы нәтижені алу негізіне
қойылуына байланысты.
Қазіргі уақытқа дейін осы жағдай тек қана есептеуіш техниканың
аспектісіне сүйенуде (клавишті басуға). Бұл тенденция өте қауіпті болып
табылады; ол математикалық модельдердің және тәсілдердің компьютерлендіру
процесінде мәнін төмендетуге, есептеуіш техникаға өте сеніп кетуге
компьютерлік эйфорияға байланысты.
Сонымен есепті шығарып жатқан ЭЕМ қолданушыға, оның шығарылуының
келесі кезеңдерін біртіндеп атқару керек (2 сурет).

Сонымен, басқарушыға, есептеуіш техниканы тек қана оны модельдеуге
үйретіп, кәдімгі құрал етуге болады; қазіргі есептеуіш техниканың
клавиштерін басып, осыдан кейін ғана ол бағдарламалық өнімдерін ой
сезіммен қолдана алады. Осы жайлы дәл айтқан кибернетика атасы Норберт
Винер болды. ЭЕМ-ді қолданудағы өте төмен нәтиженің себептері неде деген
сұраққа:
Мұның болып жатқаны, машинаға не керектігін білетін ақыл керек деп
жауап қайтарыпты. Идеалда тек қана экономикалық қатынастардың радикалдық
өзгеруі, экономика-математикалық модельдерді қолдануда бизнесмендер мен
менеджерлерге тиімді шешімдер іздеу үшін органикалық керектігін туғызады.
Бұл қазіргі ЭЕМ-нің үлкен шамаларын нәтижелі қолдануға мүмкіндік туғызады.
Сонымен, халық шаруашылығын жалпы және оның бөлек звеноларын басқарудағы
жұмысын жаңа сапалы деңгейге көтереді. ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.