Лежандр символы және квадраттық қалдықтар теориясы


КІРІСПЕ
Математика (грекше: μάθημα - ғылым, білім, оқу; μαθηματικός - білуге құштарлық) - әлдебір әлемнің сандық қатынастары мен кеңістіктік формалары, оның ішінде - структуралар, өзгерістер, белгісіздік жөніндегі ғылым. Ол абстрактілендіру және логикалық қорыту, есептеу, санау, өлшеу және физикалық нәрселерді жүйелі түрде орнықтыру, бейнелеу мен өзгерістерді оқыту арқылы көрініс табады. Математиктер жаңа тұжырымдамаларды сипаттайтын осы түсніктерді ретімен таңдалып алынған аксиомалар мен анықтамаларды пайдалана қорыта отырып зерттейді.
Қазіргі ғылым мен техникада математикалық зерттеулер, модельдер, жобалар өте үлкен роль атқарады. Ол қазіргі ақпараттар жүйесінің дамуына тікелей байланысты, демек математикалық нақты сандар шешімін табуға табысты қолдану мүмкіншілігін кеңейтеді.
Математика фундаменталды пəн, одан дəріс беру төменгі жағдайды қарастырады:
а) ойдың логикалық жəне алгоритмдік дамуын;
ə) негізгі зерттеу əдістерін меңгеру жəне математикалық есептердің шешімдерін таба білу;
б) математикалық негізгі сандық əдістерін меңгеру жəне оны компьютерде орындау;
в) математикалық білімді өз бетінше ұғып алуға еңбектену, қолданбалы инженерлік жəне экономикалық есептерге талдау жүргізу.
Таңдап отырған курстық жұмыстың басты мақсаты Лежандр символын зерттеу.
Мақсатқа жету үшін келесідей міндеттер қойылды:
- тақырып бойынша әдебиетті зерттеу;
- Лежандр символына қатысты анықтамалар мен теоремаларды дәлелдеу.
.
1 БІРІНШІ ДӘРЕЖЕЛІ САЛЫСТЫРУЛАР ЖӘНЕ САЛЫСТЫРУЛАР ЖҮЙЕСІН ШЕШУ
Бір айнымалылы салыстырудың дәрежесі
 болсын.
болсын.
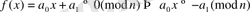 ,
,
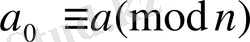 және
және
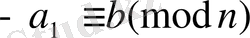 деп алсақ, онда
деп алсақ, онда
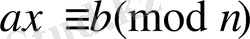 . (*)
. (*)
1) Егер
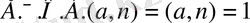 болса, онда (*) салыстыруының бір ғана шешуі болады.
болса, онда (*) салыстыруының бір ғана шешуі болады.
Эйлер теоремасы бойынша
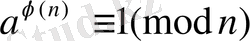 . Бұдан
. Бұдан
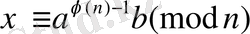 класы (*) -нің шешуі. Шынында,
класы (*) -нің шешуі. Шынында,
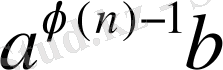 санын (*) қойсақ:
санын (*) қойсақ:
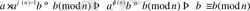 Ал, (*) -ның кез-келген шешуі
Ал, (*) -ның кез-келген шешуі
 -ны алсақ, онда
-ны алсақ, онда
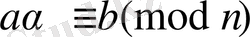 және
және
 .
.
Енді бұл екі салыстыруды жақтап көбейтсек
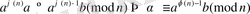 ,
,
яғни
 мен (
мен (
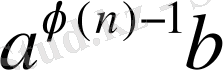 ) сандары бір класста жатады.
) сандары бір класста жатады.
2)
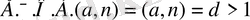 және
және
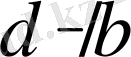 болса, онда (*) -ның шешуі жоқ.
болса, онда (*) -ның шешуі жоқ.
Шынында, қарсы жорысақ, яғни
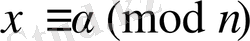 (*) -ның шешуі деп алсақ, онда
(*) -ның шешуі деп алсақ, онда
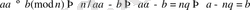
 және
және
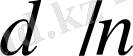 болғандықтан соңғы теңдіктен
болғандықтан соңғы теңдіктен
 шығады, ал бұл қайшылық.
шығады, ал бұл қайшылық.
3)
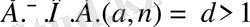 және
және
 болса, онда (*) -ның
болса, онда (*) -ның
 әртүрлі шешулері бар болады.
әртүрлі шешулері бар болады.
Мына
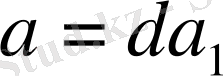 ,
,
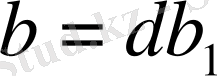 және
және
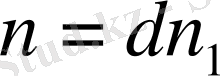 теңдіктерден және (*) -дан
теңдіктерден және (*) -дан
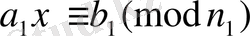 (**)
(**)
салыстыруы шығады, мұндағы
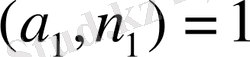 . Ендеше (**) -ның 1) -ші жағдай бойынша бір ғана шешуі бар
. Ендеше (**) -ның 1) -ші жағдай бойынша бір ғана шешуі бар
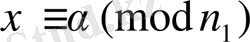 . Бұл шешу (*) -ға шешу болатындығы айқын. Өйткені
. Бұл шешу (*) -ға шешу болатындығы айқын. Өйткені
 .
.
Бірақ
 шешуі
шешуі
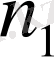 модулі бойынша анықталған.
модулі бойынша анықталған.
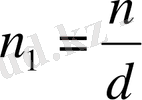 екенін ескерсек, бұл модуль бойынша мына
екенін ескерсек, бұл модуль бойынша мына
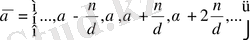
классты аламыз. Енді бұл класстың қалындылары
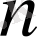 модулі әртүрлі
модулі әртүрлі
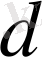 класстарға бөлінетіндігін көрсетейік. Мына
класстарға бөлінетіндігін көрсетейік. Мына
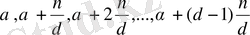 (***)
(***)
сандар
 модулі бойынша әртүрлі класстарда жататынын және
модулі бойынша әртүрлі класстарда жататынын және
 класының кез-келген саны осылардың тек біреуімен ғана
класының кез-келген саны осылардың тек біреуімен ғана
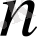 модулі бойынша бір класста болатынын дәлелдейік.
модулі бойынша бір класста болатынын дәлелдейік.
Егер
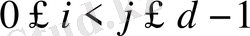 болса, онда
болса, онда
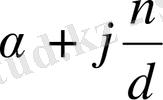
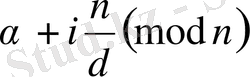 . Шынында, қарсы жорысақ, яғни
. Шынында, қарсы жорысақ, яғни
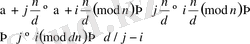
бірақ
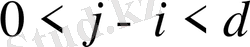 . Бұл қайшылық (***) -дағы сандар
. Бұл қайшылық (***) -дағы сандар
 модулі бойынша әртүрлі
модулі бойынша әртүрлі
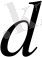 класстарда жататынын көрсетеді.
класстарда жататынын көрсетеді.
 үшін
үшін
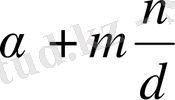 сандарын, яғни
сандарын, яғни
 класының кез-келген қалындысын алайық. Қалдықпен бөлу теоремасынан
класының кез-келген қалындысын алайық. Қалдықпен бөлу теоремасынан
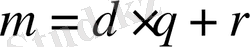 , мұндағы
, мұндағы
 . Ендеше
. Ендеше
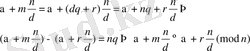
мұндағы
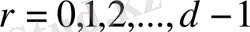 . 3-ші жағдай дәлелденді.
. 3-ші жағдай дәлелденді.
(А)

Бұл бір айнымалылы салыстырулар жүйесін шешу үшін алдымен жүйедегі әр салыстыруды қарастырып, оның шешулерін табу керек. Әр салыстырудың әр шешуін
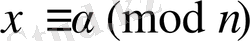 түрінде жазамыз. (А) жүйесінің шешуін табу үшін оның әр салыстыруының шешулерінің біреуін ғана алып, мына
түрінде жазамыз. (А) жүйесінің шешуін табу үшін оның әр салыстыруының шешулерінің біреуін ғана алып, мына
(В)
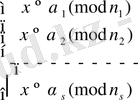
бірінші дәрежелі салыстыруларынан тұратын жүйені шешу қажет. Егер (В) жүйесі үйлесімді болса, онда (А) жүйесі де үйлесімді болады.
Егер (А) жүйесінің 1-ші салыстыруының әртүрлі шешулерінің саны
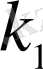 , 2-ші салыстыруының әртүрлі шешулерінің саны
, 2-ші салыстыруының әртүрлі шешулерінің саны
 ші салыстыруының әртүрлі шешулерінің саны
ші салыстыруының әртүрлі шешулерінің саны
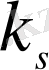 болса, онда (А) жүйесінен (В) түріндегі салыстырулар жүйелерінің саны
болса, онда (А) жүйесінен (В) түріндегі салыстырулар жүйелерінің саны
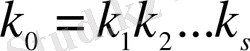 көбейтіндісіне тең болады.
көбейтіндісіне тең болады.
Ал (В) жүйесін шешу жолын біртіндеп жүргіземіз. 1-ші салыстырудан
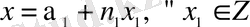
теңдігін 2-ші салыстыруға қойсақ, онда
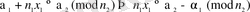
Бұл
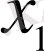 айнымалысына қарағанда
айнымалысына қарағанда
 модулі бойынша 1-ші дәрежелі салыстыру. Егер
модулі бойынша 1-ші дәрежелі салыстыру. Егер
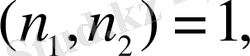 онда
онда
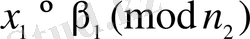 шешуі бар. Бұдан
шешуі бар. Бұдан
 теңдігін (*) ға қойып, мына
теңдігін (*) ға қойып, мына
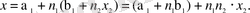
Енді соңғы (**) теңдікті (В) жүйені 3-ші салыстыруына қойып, оның
 модулі бойынша шешуін тауып, былай
модулі бойынша шешуін тауып, былай
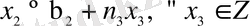 белгілеп, қайтадан (**) теңдікке қойып, 4-ші салыстыруға көшеміз. Осы процессті соңғы салыстыруға дейін жалғастыруы, (В) жүйенің шешуін табамыз.
белгілеп, қайтадан (**) теңдікке қойып, 4-ші салыстыруға көшеміз. Осы процессті соңғы салыстыруға дейін жалғастыруы, (В) жүйенің шешуін табамыз.
Теорема.
Егер жүйенің модульдері
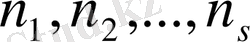 қос-қостан өзара жай болса, онда (В) жүйесінің
қос-қостан өзара жай болса, онда (В) жүйесінің
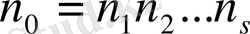 модулі бойынша бір ғана шешуі бар болады.
модулі бойынша бір ғана шешуі бар болады.
Дәлелдеу.
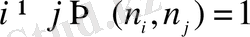 қос-қостан өзара жай модульдер үшін
қос-қостан өзара жай модульдер үшін
Е. К. О. Е.

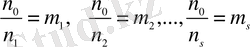 деп белгілеп, (***)
деп белгілеп, (***)
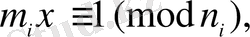 мұндағы I=1, 2, …, s, салыстыруының бір ғана шешуі бар, өйткені
мұндағы I=1, 2, …, s, салыстыруының бір ғана шешуі бар, өйткені
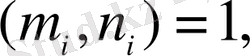 яғни
яғни
Е. Ү. О. Б.
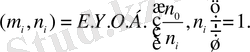
Енді (***) салыстырудың шешуін
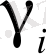 деп белгілеп, мына
деп белгілеп, мына
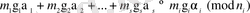
салыстыруының сол жағындағы
 үшін барлық мүшелер
үшін барлық мүшелер
 ге еселі екенін көреміз.
ге еселі екенін көреміз.
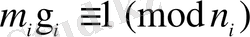 екенін ескерсек
екенін ескерсек

(В) жүйесінің шешуі
 болады және
болады және
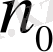 модулі бойынша бір ғана шешу шығады.
модулі бойынша бір ғана шешу шығады.
Теорема.
Егер
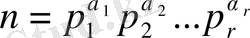 каноникалық жіктеуі болса, онда
каноникалық жіктеуі болса, онда
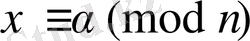
салыстыруы мына
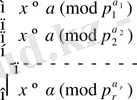
салыстырулар жүйесіне эквивалент болады.
2 ЕКІНШІ ДӘРЕЖЕЛІ САЛЫСТЫРУЛАР. ЛЕЖАНДР СИМВОЛЫ
Жоғарғы дәрежелі бір айнымалылы салыстырулардың қарапайым түрі ретінде 2-ші дәрежелі жай модуль бойынша салыстыруды алайық.
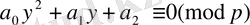 , (1)
, (1)
мұндағы модуль
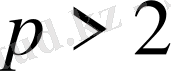 болсын. Егер
болсын. Егер
 болса, (1) салыстырудың сол жағын жұп тығын ғана анықтау жеткілікті, ал бұл ең оңай есеп болады.
болса, (1) салыстырудың сол жағын жұп тығын ғана анықтау жеткілікті, ал бұл ең оңай есеп болады.
Енді (1) салыстырудың екі жағын да
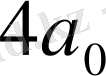 ге көбейтіп, одан кейін екі жағына да
ге көбейтіп, одан кейін екі жағына да
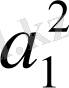 санын қоссақ, онда
санын қоссақ, онда
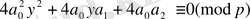 және
және

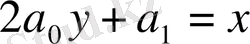 және
және
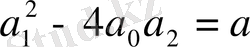 деп белгілесек, онда
деп белгілесек, онда
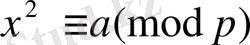 (2)
(2)
екімүшелі салыстыру шығады. Бұл салыстырудың шешуі болуы да, болмауы да мүмкін, мұндағы
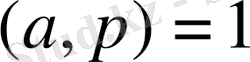 . Ал
. Ал
 болса, онда
болса, онда
 екені айқын.
екені айқын.
Анықтама.
Егер (2) салыстыруының ең болмағанда бір шешуі бар болса, онда
 саны
саны
 модулі бойынша квадраттық қалынды, ал керісінше болса, қалынды емес деп аталады.
модулі бойынша квадраттық қалынды, ал керісінше болса, қалынды емес деп аталады.
Теорема.
Егер
 саны
саны
 модулі бойынша квадраттық қалынды болса, онда (2) салыстыруының тура екі әртүрлі шешулері болады.
модулі бойынша квадраттық қалынды болса, онда (2) салыстыруының тура екі әртүрлі шешулері болады.
Дәлелдеу.
Анықтама бойынша, егер
 - квадраттық қалынды болса, онда (2) шешуі бар. Айтайық
- квадраттық қалынды болса, онда (2) шешуі бар. Айтайық
 -шешу, яғни
-шешу, яғни
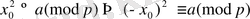 және
және
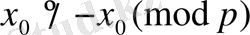 . Өйткені, егер
. Өйткені, егер
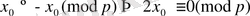 және
және
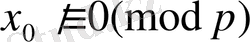 болғандықтан
болғандықтан
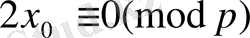 шығады. Бірақ
шығады. Бірақ
 , енді екі әртүрлі шешу бар.
, енді екі әртүрлі шешу бар.
Ферманың кіші теоремасы бойынша
 үшін
үшін
 , мұндағы
, мұндағы
 -тақ жай сан. Онда
-тақ жай сан. Онда
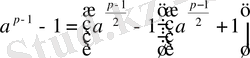 . Жай санға бөлудің қасиеті бойынша
. Жай санға бөлудің қасиеті бойынша
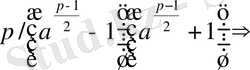 не
не
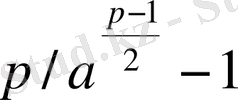 , не
, не
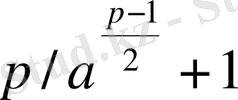 , яғни
, яғни
 , не (3)
, не (3)
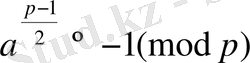 (4)
(4)
салыстырулары шығады. Ал бұл екі (3) және (4) бір уақытта орындала алмайды. Өйткені, қарсы жорысақ, онда
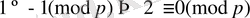 . Бұл мүмкін е мес (
. Бұл мүмкін е мес (
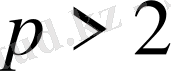 ) .
) .
Егер
 саны
саны
 модулі бойынша квадраттық қалынды болса, онда мәні 1 ге, квадраттық қалынды емес болса, онда мәні -1 ге тең Лежандр символы деп аталатын мына
модулі бойынша квадраттық қалынды болса, онда мәні 1 ге, квадраттық қалынды емес болса, онда мәні -1 ге тең Лежандр символы деп аталатын мына
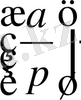 «
«
 -ның
-ның
 ға қатысты символы» деп аталады,
ға қатысты символы» деп аталады,
 символдың алымы, ал
символдың алымы, ал
 бөлімі.
бөлімі.
Теорема. (Эйлер критерийі) .
Лежандр символы
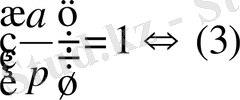
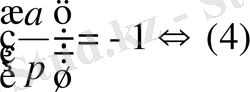 .
.
Дәлелдеуі.
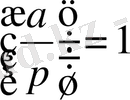 , онда
, онда
 саны
саны
 бойынша квадраттық қалынды, яғни (2) -нің тура екі әртүрлі шешулері бар. 4-ші лекциядағы теоремалар бойынша
бойынша квадраттық қалынды, яғни (2) -нің тура екі әртүрлі шешулері бар. 4-ші лекциядағы теоремалар бойынша

қалдықпен бөлудегі қалдық
 -тің коэффициенттері
-тің коэффициенттері
 ға бөлінеді. Ал
ға бөлінеді. Ал
 болғандықтан
болғандықтан
 - 1-ші дәрежелі көпмүшелік және
- 1-ші дәрежелі көпмүшелік және
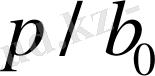 ,
,
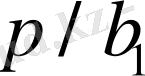 .
.
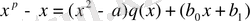 (5)
(5)
Осы теңдеуге алдымен
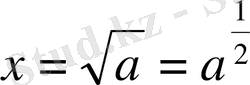 , одан кейін
, одан кейін
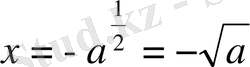 деген мәндер беріп, мына
деген мәндер беріп, мына
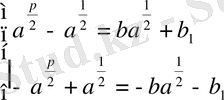
сандық тепе-теңдіктер аламыз. Енді оларды қосып және алсақ,
 және
және
 , ал бұдан (3) шығады. Керісінше, (3) деп
, ал бұдан (3) шығады. Керісінше, (3) деп
 , яғни (2) -нің екі әртүрлі шешулері бар. Ендеше
, яғни (2) -нің екі әртүрлі шешулері бар. Ендеше
 - квадраттық қалынды, ал
- квадраттық қалынды, ал
 .
.
Лежандр символының қасиеттері:
1
 . Егер
. Егер
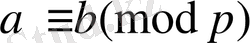 , онда
, онда
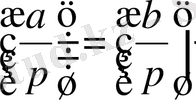 ;
;
2
 .
.
 ;
;
3
 .
.
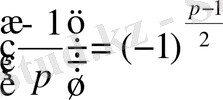 ;
;
4
 .
.
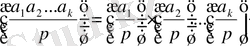 ;
;
5
 .
.
 ;
;
6
 .
.
 және
және
 әртүрлі жай сандар болса, онда
әртүрлі жай сандар болса, онда
 .
.
Енді осы Лежандр символының қасиеттерінің дәлелдеу жолдарын көрсетейік.
1
0
.

Онда а мен b сандары р модулі бойынша не квадраттық қалындылар, не екеуі де квадраттық қалындылар емес болады.
2
0
.
 , яғни 1 саны р модулі бойынша квадраттық қалынды.
, яғни 1 саны р модулі бойынша квадраттық қалынды.
3
0
.
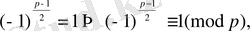 яғни -1 саны р модулі бойынша квадраттық қылынды, ал
яғни -1 саны р модулі бойынша квадраттық қылынды, ал
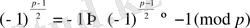 болса, онда -1 саны қылынды емес.
болса, онда -1 саны қылынды емес.
4
0
. Айтайық,
 сандарының ішінде
сандарының ішінде
 сандары р модулі бойынша квадраттық қалындылар, ал
сандары р модулі бойынша квадраттық қалындылар, ал
 сандары квадраттық қалынды емес болсын. Онда
сандары квадраттық қалынды емес болсын. Онда
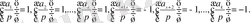 Эйлер критерийі бойынша
Эйлер критерийі бойынша
 Equation. 3 мұндағы I=1, 2, …, s.
Equation. 3 мұндағы I=1, 2, …, s.
 Equation. 3 мұндағы j=s+1s+, 2, …, k
Equation. 3 мұндағы j=s+1s+, 2, …, k
Бұл салыстыруларды көбейтсек, онда мына
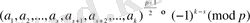
салыстыруы шығады. Егер
 болса, онда
болса, онда
 ал
ал
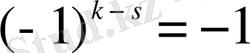
болса, онда
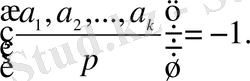 Ендеше,
Ендеше,
 ал
ал

Соңғы екі теңдіктерден 4
 қасиеттің дәлелденгенін көреміз. 5
қасиеттің дәлелденгенін көреміз. 5
 және 6
және 6
 қасиеттерді дәлелдеу үшін алдымен төмендегі Гаусс леммасын қарастыруымыз керек.
қасиеттерді дәлелдеу үшін алдымен төмендегі Гаусс леммасын қарастыруымыз керек.
Лемма. Егер p>2 жай саны үшін Е. Ү. О. Б. (a, p) =1болса, онда
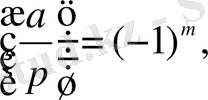 мұндағы m саны (*)
мұндағы m саны (*)
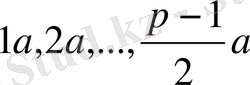 сандарын p-ға бөлгендегі
сандарын p-ға бөлгендегі
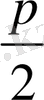 ден үлкен қалдықтардың санын көрсетеді.
ден үлкен қалдықтардың санын көрсетеді.
Дәлелдеу. (*) -дағы сандар p модулі бойынша әртүрлі класстарда жататынын көрініп тұр. Ендеше оларды p-ға бөлгендегі қалдықтар да әртүрлі класстарда жатады.
(*) -дағы p-ға бөлгенде
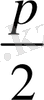 санынна үлкен қалдықтарды
санынна үлкен қалдықтарды
 ал
ал
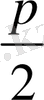 деп кішілерін
деп кішілерін
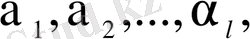 деп белгілейік, мұндағы l+m=
деп белгілейік, мұндағы l+m=
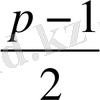 және l>0 де m>0 деп есептейік. Онда
және l>0 де m>0 деп есептейік. Онда
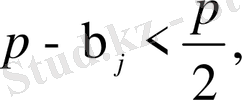 мұндағы
мұндағы
 яғни
яғни
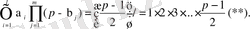
Екінші жағынан (*) -дағы сандарды p-ға бөлгендегі әр қалдық солардың біреуімен ғана p модулі бойынша салыстыруы, яғни

Ал,
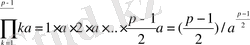 Equation. 3
Equation. 3
болғандықтан (***) деп мына
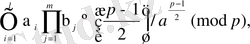 Equation. 3 және (**) -дан
Equation. 3 және (**) -дан
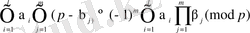 Equation. 3 салыстырулары шығады.
Equation. 3 салыстырулары шығады.
Соңғы екі салыстырулардан және (**) теңдіктен
 Equation. 3 ал бұдан
Equation. 3 ал бұдан
 шығады.
шығады.
Ендеше m жұп болса, онда
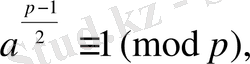 Equation. 3 ал m тақ болса, онда
Equation. 3 ал m тақ болса, онда
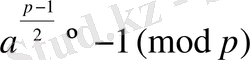 Equation. 3
Equation. 3
Сондықтан,
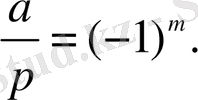
5
 . Лемманың дәлелдеуіндегі (*) сандарын p-ға бөлгендегі қалдықтарды бұрынғыдай белгілесек, және қалдықпен бөлу туралы теореманы ескерсек, онда
. Лемманың дәлелдеуіндегі (*) сандарын p-ға бөлгендегі қалдықтарды бұрынғыдай белгілесек, және қалдықпен бөлу туралы теореманы ескерсек, онда
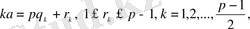 Equation. 3 ал
Equation. 3 ал
 -бүтін бөлігі.
-бүтін бөлігі.
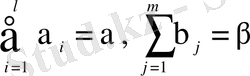 Equation. 3 деп алсақ, онда
Equation. 3 деп алсақ, онда
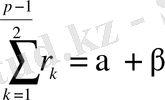 және
және

теңдіктері алынады., яғни
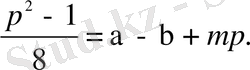
Енді,
 және соңғысынан алдындағын алсақ, онда
және соңғысынан алдындағын алсақ, онда
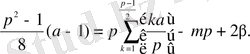 теңдігі шығады.
теңдігі шығады.
Бұдан
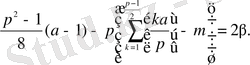 және p>2үшін p
және p>2үшін p
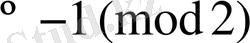 Equation. 3
Equation. 3
болғандықтан

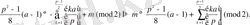
Ендеше,
(-1)
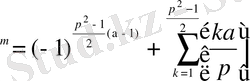 Equation. 3 .
Equation. 3 .
Ал, a=2
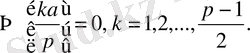 Equation. 3
Equation. 3
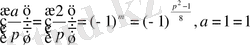
6
 Equation. 3 .
Equation. 3 .
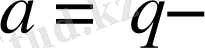 Equation. 3 жай сан және
Equation. 3 жай сан және
 q>2, онда
q>2, онда
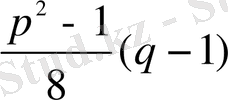 Equation. 3 -жұп сан. Сондықтан,
Equation. 3 -жұп сан. Сондықтан,
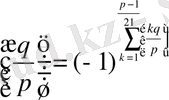 және
және
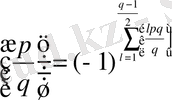 ,
,
мұндағы (p, q) =1, яғни өзара жай.
Бұл екі теңдіктерді көбейтіп, мына
 теңдік алынады. Енді,
теңдік алынады. Енді,
 теңдіктің орындалатынын көрсетсек, онда 6
теңдіктің орындалатынын көрсетсек, онда 6
 -қасиеттің орындалатыны оңай шығады. Ол үшін lp-kq түріндегі сандарды қарастырамыз. l=1, 2, …,
-қасиеттің орындалатыны оңай шығады. Ол үшін lp-kq түріндегі сандарды қарастырамыз. l=1, 2, …,
 ал k=1, 2, …,
ал k=1, 2, …,
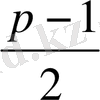 болғандықтан ол сандардың саны
болғандықтан ол сандардың саны
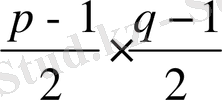 көбейтіндісіне тең болады және
көбейтіндісіне тең болады және
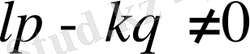 . Шынында да, егер
. Шынында да, егер
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz