Қозғалысқа берілген есептер

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 31 бет
Таңдаулыға:

Тақырыбы: Қозғалысқа берілген есептерді шығарауға үйрету

МАЗМҰНЫ

І КІРІСПЕ 3
ІІ
Негізгі бөлім
2.1
Бастаауыш мектепте қозғалыс есептерін оқытудың теориялық негіздері 6
2.2
Қозғалысқа берілген есептердің негізгі түрлері 14

2.3
Бастауыш сынып оқушыларының логикалық ойлау қабілетін дамытуда қозғалысқа берілген есептердің маңызы 24
ІІІ
Тәжірибелік бөлім 27
ІV
Қорытынды 30
V
Пайданылған әдебиеттер 32

КІРІСПЕ

Зерттеудің көкейкестілігі
Қазіргі таңда білім беру жүйесін реформалаудың маңызды бағыттары қатарынан білім сапасын көтеру мәселесі жетекші орын алады.Жалпы білім беретін мектептерде білім сапасын арттыру,білім беру мазмұнын жетілдіру,оқыту үрдісін жаңа сапалық деңгейге көтеру мұғалімдердің әдістемелік шеберліктерін арттыру сияқты факторлармен байланысты.
Соңғы жылдарда педагогикалық процесті ізгілендіру тенденцияларын күшейтуі математика пәндерін оқытуға аса көңіл бөлініп,болашақ ұрпақтың техникалық білімдерінің терең болуын талап етіп отыр.
Қазақстан Республикасының Президенті Н.Ә.Назарбаевтың Қазақстан халқына жолдауында:
Білім беру реформасы - Қазақстанның бәсекеге нақтылы қабілеттілігін қамтамасыз етуге мүмкіндік беретін аса маңызды құралдардың бірі.
Бізге экономикалық және қоғамдық жаңару қажеттіліктеріне сай келетін осы заманғы білім беру жүйесі қажет.
Жоғары білім беру саласында техникалық білім беруді дамытуға ерекше назар аудара отырып,Жоғары оқу орындары желісінде оңтайландыру жүргізілуге тиіс.Осы заманғы мемлекеттік мамандар даярлау үшін Мемлекеттік басқару академиясының негізінде шетелдік серіктестіктердің қатысуымен ең жоғарғы стандарттарға сәйкес келетін ұлттық басқару мектебі құрылуы қажет.
Білім беру жүйесін дамытуды ынталандыру мақсатында және сектор мен мемлекет арасындағы серіктестікті нығайту мемлекеттік жекеменшілік білім беруге кредиттер бөлу жүйесін жетілдіру қажет,-делінген.
Ал,оның негізі бастауыш сыныпта қаланбақ.Сондықтан да,бастауыш сынып оқушыларының ой-өрісін,ізденісін,тапқырлығын,зер ектігін дамытуда қозғалысқа берілген есептердің маңызы зор.Қазіргі кезде көптеген мұғалімдерге,әсіресе,бастауыш сынып оқытушыларына сабақта фронтальды жұмыс істеу міндеті қойылды.Өйткені,сабақ кезінде оқушылардың басым көпшілігі мұғалімнің нұсқауымен есептерді шешуге енді кіріскенде,сыныптағы басқа оқушылар есептің шешімін тауып қояды.Кейбір оқушылар есептің шешімін тауып қана қоймай,есептің әр түрлі шешімдерін көруге қабілетті болады.Ал оқушылардың ендігі бір бөлігіне жай ғана тапсырманы шешудің өзіне едәуір көмек керек болады.Иә,көмекке мұқтаждық әр оқушыда әр түрлі болады.Бұл ретте сыныптың бір бөлігі сабаққа қатыстырылмай қалуы мүмкін,өйткені ұсынылып отырған міндеттер олар үшін тым оңай болып табылады.Осыған байланысты мынандай сұрақ туындайды: Сабақта қозғалысқа байланысты есептермен жұмыс істеуді оқушылардың мүмкіндіктеріне сай келетіндей қалай ұйымдастыруға болады?

Қозғалысқа берілген есептердің көпшілігі 4-сынып бағдарламасында берілген.Бұл сыныптың бірінші жарты жылдығында оқушылар жалпы

ұғыммен таныстырылып,мағлұмат беріледі,яғни қозғалысқа берілген есептердің шешілу жолын үйренеді.Жылдамдық пен уақыттың көбейтіндісі қашықтықты беретіндігін, қашықтықты уақытқа бөлгенде жылдамдық алынатындығын және қашықтықты жылдамдыққа бөлгенде уақыт алынатындығын оқушылар меңгеретін болса,жылдың екінші жартысында қозғалысқа берілген есептерді шығару дағдыларын қалыптастырып,бекіту үшін қарастырылған есептердің берілгендігі бәрімізге мәлім.Балалар қозғалысқа берілген есептер туралы жыл бойына оқығанымен,машық кезінде оқушылардың есепті шығару деңгейлерінің төмендігін байқағандықтан курстық жұмысымда олардың деңгейлерін көтеру үшін есептің мазмұнын түсініп оқуға және толық талдауға көңіл бөлдім.
Сонымен,жоғарыда аталған мәселелерге байланысты таңдалған курстық жұмысымның тақырыбы- Қозғалысқа байланысты есептермен жұмыс.

Курстық жұмысымда қозғалысқа байланысты есептермен жұмыс істеу кезінде оқушылардың логикалық ойлау қабілетін дамыту,оқушының білімге деген ынтасын арттыру және қозғалыс есептерін шығарудың әдістерін зерттеу және оны есеп шығару барысында қолдану мәселелері қаралды.
Зерттеу мақсаты: Бастауыш сыныптарда қозғалысқа берілген есептердің ерекшеліктерін анықтау.
Оқушыларға қозғалыс есептерімен жұмыс істеу әдістемесін меңгерту;оқушы білімін дамыта отырып,оның іс-әрекетін тиімді ұйымдастыра білу. Бастауыш
сыныпта математика сабағында есептің мазмұнын түсініп оқуды және толық талдауды қолдану арқылы оқушылардың пәнге деген қызығушылығын арттыру жолдарына талдау жасау. Зерттеу міндеттері: -
Сабақта қозғалыс есептерімен жұмыс істеуді ұйымдастыру мәселесі бойынша әдістемелік әдебиеттерді зерделеу және талдау; - Балалардың есеп шығарудағы математикалық білімін белгілі бір жүйе бойынша дамыту мүмкіндіктерін анықтау;
- Балалардың есеп шығарудағы ой-өрісін дамытудың тиімділігін тексеру;
Зерттеу объектісі - Бастауыш мектептегі математиканы оқыту процесі.
Зерттеу пәні - Бастауыш сыныптағы математика сабағында қозғалыс есептерін шығару тәсілдерін қолдану арқылы оқушылардың ой-өрісін дамыту жолдары мен әдістері.
Зерттеудің ғылыми болжамы - Егер бастауыш сыныпта математика сабағында қозғалыс есептерін шығару тәсілдеріне талдау жасауды қолдану арқылы оқушылардың ой-өрісі дамытылатын болса,онда олардың математикадан білім деңгейі жоғарылайды,өйткені пәнге деген қызығушылығы нәтижелі қалыптасады.
Жұмыстың практикалық маңыздылығы - Бастауыш мектепте математика сабағындағы есептеуді үйретудің және оны оқытудағы әдістемелік

тәсілдердің мүмкіндіктерін ашып,қолдану жолдарын білімгер өзі әдістерін құру арқылы ұсынады.
Зерттеудің теориялық мәні - Қозғалыстың жалпы даму тарихына, бастауыш сынып оқушыларына қозғалыс есептерін шешуді оқытудың әдістемелік тәсілдеріне,қозғалыс есептерінің ерекшеліктеріне шолу жасалынды.
Зерттеудің методологиялық негізі - Бастауыш сыныптардағы қозғалыс есептерін үйрету сабағын жүргізудің қажеттілігі мен пайдасын анықтап көрсетті.
Курстық жұмысымда зерттеу әдістерінің келесі түрлері қолданылды:
Әдістемелік және психологиялық-педагогикалық әдебиеттерді зерделеу және талдау;
Педагогикалық жұмыста озық тәжірибені талдау және қорыту;
Бастауыш сыныптың математика сабағына бақылау және талдау жасау.

БАСТАУЫШ МЕКТЕПТЕ ҚОЗҒАЛЫС ЕСЕПТЕРІН ОҚЫТУДЫҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ

Қозғалыс - заттар мен құбылыстардың жалпы өзгерісін,бір-біріне әсер етуін білдіретін ұғым. Қозғалыссыз өмір болмайды, ол-барлық нәрсенің өмір сүру тәсілі.
Антиктік заман философиясы қозғалыстың бар екенін мойындап қана қоймай,оның мәнін зерделеп,себептерін,жалпы заңдылықтарын ашуға ұмтылды.Кейбір философтар табиғат бастамасын ағып жатқан суға (Фалес),жалындаған отқа (Гераклит),сандар арасындағы үйлесімге (Пифагор),бос кеңістіктегі атомдарға (Демокрит) теңеп,дүниенің динамикалық суреттемесін жасаса,енді біреулер қозғалыс ұғымының қайшылыққа толы екенін (Зенон) айтты.
Аристотель ілімінде қозғалыс ұғымы категория деңгейіне көтеріліп,оның көптүрлілігі,болмыс пен танымның басты анықтамаларының бірі екендігі айтылды.Жаңа заман дәуірінде (17-18 ғ.) ғылыми танымның,әсіресе,механиканың қарқынды дамуына орай қозғалыс көбінесе денелердің кеңістікте орын алмасуы және бір-біріне әсер етуі ретінде қарастырылып,дүниенің механикалық суреттемесі жасалды.
Гегель қозғалыс ұғымын қалыптасу,өзгеру,даму ұғымдарымен ұштастырып,оның жалпы заңдарын ашты,оны сан мен сапаның өзгеруі,сапалық түрлендіру секілді түсініктермен байытып,қозғалыстың ішкі қайнар көзі қайшылықта екенін көрсетті.Дүниеде өзгермейтін,қозғалмайтын дене болмайтыны секілді,қозғалыс табиғаттағы,қоғамдағы барлық өзгерістерді түгел қамтиды.Қозғалыс-жалпы өзгеріс,нысандардың бір-біріне әрқалай әсер етуі және олардың қалпының ауысуы.Ол-материяның ажырамас өмір сүру тәсілі.Қозғалыссыз материяның болмайтыны секілді,материясыз қозғалыстың болуы мүмкін емес.Қозғалыс сан алуан болып келеді.Әрбір қозғалыстың өз иесі,өз тасымалдаушысы,яғни түпкі негізі болады.Мысалы,қарапайым бөлшектер қозғалысының өз заңдылықтары,өзіне ғана тән ерекшеліктері бар.Сол секілді материя құрылымының деңгейіне сәйкес өз қозғалысының болуы заңды.
Алайда,қозғалыстың бастапқы негізін анықтау,яғни алғашқы қозғалыс қалай пайда болды деген мәселеде ғылыми ой-пікірлер мен діни сенімге негізделген теориялар қайшылығы жалғасып келеді. Қозғалыс шектілік пен шексіздіктің,өзгермелілік пен орнықтылықтың, тыныштық пен тынышсыздықтың қайшылығы болып табылады. Қозғалыстың өзіне қарама- қарсы сәті - тыныштық. Ол-қозғалыстың белгілі бір өткінші қалпы,біршама тұрақтылығы. Шексіз тыныштыққа жету - заттың жойылып кетуімен бара-бар келеді. Дамумен салыстырғанда қозғалыс - неғұрлым жалпылама ұғым,өйткені ол жүйенің дамуының ішкі заңдарына сәйкес келмейтін қандай да бір сыртқы және кездейсоқ өзгерістерді қамтиды.
ХХ ғасырдың екінші жартысында ғылым мен техниканың,қоғамдық

тәжірибенің дамуы жаңа нысандарды, күрделі жүйелер кешенін зерттеуге,қозғалыс және оның түрлері, олардың өзара байланысы туралы жаңа философиялық теориялар жасауға жол ашты.

Қозғалысқа берілген есептер

Бастауыш сыныпта қозғалысқа берілген есептердің көпшілігі 4-сынып бағдарламасында қарастырылады.
Бұл түрдегі есептердің негізгі компонеттері: а) жүрілген жол (S);
б) жылдамдық (V); в) уақыт (T).
Бұл шамалардың арасындағы байланыс келесі формулалармен өрнектеледі:
s=v*t ; v=s:t ; t=s:v.
Бұл шамалар бір бірлік жүйесінде болулары керек.Мысалы, егер жол километр-мен,ал уақыт сағат-пен есептелетін болса,онда жылдамдық кмсағ- пен есептеледі.
Қозғалысқа байланысты есептерді шығаруға дайындық жұмысы оқушылардың қозғалыс туралы түсінігін қорытуды,жаңа шамалармен- жылдамдық,уақыт,қашықтықпен танысуын,осы шамалардың арасындағы байланыстарды айқындай түсу жағын қарастырады.
Енді қозғалысқа берілген есептердің негізгі компоненттеріне жеке-жеке тоқталайық.
Жылдамдық - қозғалыстың негізгі математикалық сипаттамаларының бірі,қозғалыстың уақыт бойынша өзгеруінің лездігі.Жылдамдық латынның V әрпімен белгіленеді.Жалпы формуласы: V=S:T (мұндағы S - қашықтық, T
уақыт).Жылдамдықты,әдетте, мс-пен (бірліктердің халықаралық жүйесінде),кейде ммин-пен, кмсағ-пен өлшейді.
Уақыт - оқиғаның ұзақтығын және тізбектілігін сипаттайтын математиканың негізгі түсініктерінің бірі.Уақыт оқиғаларды реттеуде, олардың ұзақтығын,заттардың қозғалысын сипаттауда қолданылады.Уақыт латынның T әрпімен белгіленеді.Жалпы формуласы: T=S:V (мұндағы S
қашықтық,V - жылдамдық).Өлшем бірліктері - секунд,минут,сағат.
Қашықтық - математикадағы маңызды геометриялық ұғымдардың бірі. Ол қозғалыста шапшаңдықты сипаттайды.Қашықтық латынның S әрпімен белгіленеді.Жалпы формуласы: S=V*T (мұндағы V - жылдамдық,T - уақыт). Негізгі өлшем бірліктері - метр,километр.
Жылдамдық,уақыт,қашықтық шамалары арасындағы байланыстарды анықтау басқа пропорционал шамалар арасындағы байланыстарды анықтау әдістемесімен жүргізіледі.Осы жұмыстың нәтижесінде балалар мынадай байланыстарды ұғынулары тиіс: егер қашықтық пен жүрілген уақыт белгілі болса,онда жылдамдықты жүріп өтілген қашықтықты уақытқа бөлу арқылы табуға болады;егер жылдамдық пен жүрілген уақыт белгілі болса,онда

қашықтықты жылдамдық пен уақытты көбейту арқылы табуға болады;егер қашықтық пен жылдамдық белгілі болса,онда жүрілген уақытты қашықтықты уақытқа бөлу арқылы табуға болады. Бұдан әрі қарай,осы білімдерге сүйене оты рып балалар қозғалысқа берілген есептерді шығарады. Осы есептермен жұмыс жасағанда сызба түріндегі иллюстрацияны жиірек пайдалану керек,өйткені ол сызба есепте айтылған жағдайды адамның көз алдына келтіруде көмектеседі.Ол үшін балалардың транспорттық қозғалысын бақылауға арналған арнайы экскурсия өткізген пайдалы.Экскурсиядағы және сыныптағ ы жұмыста балалар өздерінің транспорттық қозғалысын иллюстрациялап көрсетеді.Мысалы, оқушылар екі дененің кездесу қозғалысын мынадай көрнекілік бойынша көрсетеді:

Мұндағы,кесінді денелер кездескенге дейінгі жүрілген жолды көрсетсе,жалауша - кездескен орынды, А және В нүктелері - денелердің шыққан пункттерін,стрелкалар - қозғалыс бағыттарын көрсетеді.
Оқушыларды жылдамдықпен,уақытпен және қашықтықпен таныстырғанда өздерінің жаяу жүргендегі жылдамдықтарын,қашықтығын немесе уақытын таба білетіндей етіп ұйымдастыру керек.Ол үшін аулада немесе спорт залында тұйық жол сызып, жол бойына әр 10 метр қашықтықты белгілеу керек,содан кейін әр оқушы қандай жол жүргенін,қанша уақытта жүріп өткендігін және қандай жылдамдықта жүргенін табу керек.
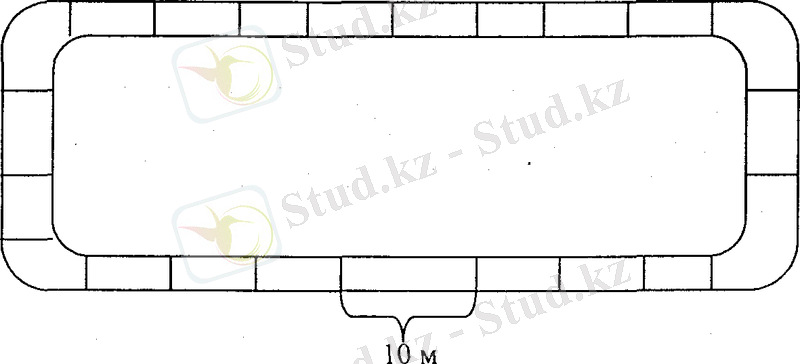Тұйық жолды көрнекілік бойынша көрсетейік.Мұғалім балаларға 4 минут жол жүруді ұсынады:
Балалар 10 метрлік белгі бойынша 10 минутта жүретінін есептеп табады.Мұғалім оқушы 1 минутта жүріп өткен қашықтық оның жылдамдығы болатынын айтады.
Аталған есептерді шығарумен қатар 4-сыныпта бір бағыттағы қозғалысқа,бір-біріне қарама-қарсы бағыттағы қозғалысқа және бірінен-бірі қарама-қарсы бағыттағы қозғалысқа арналған есептер енгізіледі.Осы есептердің әрқайсысы берілген мәліметтер мен ізделінді шамаларға

байланысты 3 түрлі болады:
Бірінші түрі - денелердің әрқайсысының жылдамдығы және қозғалыс уақыты берілген,ізделінді шама - қашықтық;
Екінші түрі - денелердің әрқайсысының жылдамдығы және қашықтық берілген,ізделінді шама - уақыт;
Үшінші түрі - денелердің әрқайсысының қашықтығы және қозғалыс уақыты берілген,ізделінді шама - жылдамдық.

Қозғалысқа байланысты есептерді шешу жолдары

Математикалық есептерді шешуде кез-келген адамдарда туындайтын мәселелерді шешу және олардың алдын алу бұрыннан оқытылып келеді.Бірақ осы уақытқа дейін олардың жалпы қабылданған түсініктемесі жоқ.
Қозғалыс есептерін шығару әдістерін қарастыру алдында,қазіргі кезде қолданылып жүрген есеп шығарудың жалпы методикасына тоқталайық.
1. Есептің шартымен танысу
Есепті шешуге арналған жұмыс алдымен оның мазмұнымен танысудан басталады.Есептің мазмұнымен таныстыру дегеніміз - оны оқып шығып,онда келтірілген жайттардың өмірде болатын ситуацияларын көз алдына келтіру.Есепті дұрыс түсіну үшін есеп мәтінін әрбір оқушы жеке-жеке оқуы тиіс.Есепті,әдетте,оқушылар оқиды.Мұғалім есепті тек балаларда есептің тексті жоқ жағдайда немесе олар оқи алмайтын кезде ғана оқиды.Егер есептің шарты шиеленіскен болса,онда оқушыға есептің шартын оқып,оны ойша елестетіп түсінуі үшін уақыт (1-2 минут) беру керек.Есепті дұрыс оқи білудің маңызы зор.Егер есептің текстінде түсініксіз сөздер кездессе,онда оларды түсіндіру керек немесе есепте айтылатын нәрселердің, мысалы , бульдозер,шөп шапқыш машинаның суреттерін көрсету керек.Есепті балалар бір-екі рет,кейде одан көп оқып шығады,бірақ біртіндеп оларды есепті бір оқығанда есте сақтап қалатындай етіп үйрету керек,өйткені бұлай еткенде олар бірден зейін қоя оқитын болады.Есептің шартын оқу кезінде оқушылардың логикалық ойлауын дұрыс қалыптастыра білу керек.Бұл математикалық терминдерді,белгісіз шамаларды түсінуге көмектеседі. Мәтінді есеппен жұмыс істеу кезінде оқушы әр сөзге,әр санға назар аударуы қажет.Мәтінмен ауызша жұмыс жасалғаннан кейін оны математикалық терминдерге (схема,кесте,сызба...) айналдыру керек.Есептің қысқаша шартын құру барысында белгілі шамалар мен белгісіз шамалардың арасындағы байланыс анықталады.Содан кейін оқушылар қандай шаманы табу керектігін біле алады.
2. Есептің мазмұнын талдау және шешімін іздеу
Есептің мазмұнымен танысқаннан кейін оның шешімін іздестіруге кірісуге болады:оқушылар есепке кірістірілген шамаларды,берілген сандар мен ізделінді сандарды айқындай білуі тиіс,сөйтіп осылардың негізінде сәйкес арифметикалық амалдарды таңдап ала білулері тиіс.Жаңа түрдегі есепті енгізгенде оның шешуін табу жұмысына мұғалім басшылық жасайды,сонан

кейін мұны оқушылар өздігінен орындайды.Екі жағдайда да балалардың шамаларды,берілген және ізделіп отырған сандарды мүшелерге бөлуге көмектесетін,олардың арасындағы байланыстарды тағайындайтын арнайы әдістер пайдаланылады.Мұндай әдістерге есептерді иллюстрациялау , есептерді қайталау,есепті шығару жоспарын талдау және оны құру жатады. Есептердің шешімін іздеуде мәтінге талдау жасау ең көп тараған тәсілдердің бірі.Есептерді талдау ойлау тізбегі арқылы жүзеге асады.Талдау кезінде есептердегі белгілі және белгісіз шамалардың арасындағы байланысты анықтау керек.Кейін жоспар құрылады.Ойлау бұл кезде кері тәртіппен жүргізіледі.Есептерді талдауды аналитикалық-синтетикалық әдіспен жүргізуге де болады.
Есептерді мұғалім түсіндіре отырып шығару керек.Мысалы:
Мектеп пен үйдің арасы 300 м.Оқушы минут сайын 60 м жүреді.Ол 3 мин жүрді.Мектепке жету үшін ол тағы неше метр жүруі керек?

Үй
T=3 мин
Мектеп
300 м
Есепті оқыған соң мәтін бойынша әңгіме жүргізіледі.Оқушылар тақтада және дәптерлерінде мұғалімнің көмегімен есептің шартының моделін құра бастайды.Мәтін бойынша сұрақ қоя отырып,мұғалім дауыс ырғағымен тірек сөзді бөліп оқиды.
Жазуды орындаймыз.Модельдің бірінші жолы:
Болғаны - 300 м
Оқушы қанша метр жолды жүріп өтті? (Белгісіз)
Жүріп өткен жол туралы не білеміз? (Оқушы минут сайын 60м жүреді) Оқушы жолда қанша уақыт болды? (3 минут)
Жазылу моделі:
Жүргені - ? м,минут сайын 60 м,3 мин
Есептің сұрағы қандай? (Мектепке жету үшін,ол тағы неше метр жүруі керек?)

Жазылу моделі:
Қалғаны - ? м
Мәтінді есеппен жұмыс істеу нәтижесіндегі соңғы жазылу моделі: Болғаны - 300 м
Жүргені - ? м ,минут сайын 60 м ,3 мин Қалғаны - ? м
Мәтінді есеппен жұмыс істеудің келесі кезеңі - оны шығару жоспарын құру.

Ол үшін моделі бойынша есепті талдаймыз.Бұл жағдайда мақсатты талдауды пайдаланамыз (сұрақтан берілгенге қарай).Мұғалім сыныпқа сұрақ қойып әңгімелесе отырып,есепті талдау сызбасын салады.
Есепте нені білу керек? (Оқушыға мектепке дейін жүретін қанша жол қалды?)

Қанша қалғанын білу үшін не істейміз? (Арақашықтық қанша еді және оқушы қаншасын жүріп өтті?)
Қалған жолды қандай амал арқылы табамыз? (Азайту)
Үйден мектепке дейінгі ара қашықтықты білеміз бе? (Иә,300 м)
Оқушы қанша жол жүріп өткенін білеміз бе? (Жоқ.Бірақ ол әр минут сайын 60 м жол жүргенін білеміз)
Оқушы жолда қанша уақыт болды? (3 минут)
Жүріп өткен жолын қандай амалмен табамыз? (Көбейту)
Егер есепті синтезді қолданып талда сақ (берілген сұраққа қарай),онда әңгімеміз мына түрде болады:
Оқушы әр минут сайын 60 м жүргенін білеміз және жолда барлығы 3 минут жүрген,біз нені біле аламыз? (Жүріп өткен жолды)
Жүріп өткен жолын қандай амалмен табамыз? (Көбейту)
Үйден мектепке дейінгі қашықтық 300 м екенін білеміз және жүріп өткен жолын біле отырып,енді нені таба аламыз? (Оқушы мектепке дейін неше метр жол жүруі керек?)
-Қалған жолды қандай амалмен табамыз? (Азайту)
Келесі кезеңде екі амалды орындау керек.Мәтінді есептермен жұмыс істеудің келесі кезеңі - оны шығару жоспарын орындау.
Есепті амалдарды орындау арқылы шығаруға болады (түсіндіре отырып немесе түсіндірмей де),сол сияқты өрнек құрып та шығаруға болады.
Берілген есепті амалдар арқылы шығаруды жазайық:
1) 60*3=180 м - оқушы жүріп өтті 2) 300 - 180=120 м
Енді есепті шығаруды өрнек түрінде жазып көрсетейік: 300 - 60*3=300 - 180=120 м
Жауабы: 120 м жол жүруі керек.
1. Есепті жалпы түрде шығару
Есептегі белгілі және белгісіз шамалар анықталғаннан кейін есептің қысқаша шарты құрылады.Белгісіз шаманы табуға қажетті формула анықталады.
2. Есептеу
Есепте берілген шамалардың барлығын ХБЖ өлшемдеріне келтіру керек.Кейін формулаға шамалардың сандық мәндерін қойып,математикалық есептеулер жүргізу қажет.
3. Есептің шешімін тексеру
Есептің шешімін тексеру - бұл есептің дұрыстығын немесе қате орындалғанын белгілеу.Тексеру кезінде ақыл-ой іс-әрекеттерін және практикалық іс-әрекеттерді пайдалана отырып,қорытынды ой шығарылады:

олай болса ... ,бұл есеп дұрыс (немесе дұрыс емес).Егер есеп әр түрлі тәсілдермен шешілген жағдайда есептердің шешімдері бірдей болса,онда есеп дұрыс шешілген болып есептеледі. Мысалы:
Екі ауыл арасындағы қашықтық 13 км,ауылдан бір мезгілде бір-біріне қарама-қарсы бағытта екі мотоциклші шықты және 5 минуттан кейін кездесті.Бірінші мотоциклші минутына 1 км 200 м жол жүрді.Екінші мотоциклші минутына қанша метр жол жүрген?
1км=1000м S=V*T Шешімі:
S1=V1*T=1200*5=6000м S2=S-S1=13000-6000=7000м V2=S2:T=7000:5=1400ммин
Тексеру: V=S:T=13000:5=2600ммин V2=V-V1=2600-1200=1400ммин
Жауабы: 1400 ммин Есеп дұрыс шешілген 6.Есепті шешу кезіндегі шығармашылық жұмыс
Шығармашылық сипаттағы есептерге қиындығы жоғары есептер,әр түрлі тәсілдермен шығарылатын есепт ер,бірнеше шешімі бар есептер жатады.Қиындығы жоғары есептер оқушылардың ойша есептеуіне,есептегі шамалар мен деректердің арасындағы байланысты ұғынуына көмегін тигізеді.Есептердің көпшілігі әр түрлі тәсілмен шешіледі.Есептердің әр түрлі шешімдерін іздеу оқушылардың есепт егі шамалар арасындағы жаңа байланыстарды ашуына мүмкіндік береді.
Кейбір шамалары жеткіліксіз немесе артық шамалары бар есептермен жұмыс істеу кезінде оқушылар шамалардың арасындағы байланысты терең ұғынуға үйренеді.Кейбір есептерді шешкеннен кейін оқушыларға есептің шартындағы қойылған сұрақты өзгертуді ұсынудың пайдасы мол.
Мысалы: Мәскеуден және Киевтен екі пойыз бір мезгілде бір-біріне қарама-қарсы бағытта жолға шықты.Мәскеуден шыққан пойыз 68 кмсағ жылдамдықпен,ал Киевтен шыққан пойыз 75 кмсағ жылдамдықпен жүрді.Егер Мәскеу мен Киевтің арақашықтығы 858 км болса,онда пойыздар бір-бірімен неше сағаттан кейін кездеседі?
Есеп шешіліп болғаннан кейін сұрақты мынадай етіп өзгертуге болады:
Пойыздар Мәскеуден қандай қашықтықта болғанда кездесті?, Кездесуге дейін әрбір пойыз қанша жол жүрген? және т.б.
Қозғалысқа берілген мәтінді есептер - ауызша моделі бар процестердің бірі.Барлық мәтінді есептерде бірдей тапсырма толығымен сипаттала бермейді,тек тапсырманың ең маңызды сандық сипаттамалары беріледі.
Мысалы,Автомобиль А пунктінен 60 кмсағ жылдамдықпен жолға шықты.2 сағаттан кейін оның артынан екінші автомобиль 90 кмсағ жылдамдықпен шықты.Екінші автомобиль біріншісін А пунктінен қандай қашықтықта қуып жетеді? Тапсырмада екі автомобильдің қозғалысы сипатталады.Кез-келген қозғалыс 3 шама арқылы сипатталады:жүріп өтілген қашықтық,жылдамдық және уақыт.Аталған тапсырмада кейбір шамалар белгілі болса,ал кейбірін табу қажет(жүріп өтілген қашықтық).

Осылайша,мәтінді есептердің кейбір құбылыстардың қандай да бір компоненттеріне сандық сипаттама беруге мүмкіндігі бар.
Л.М.Фридман қозғалыс есептерінің құ рамын талдап,олардан келесі компоненттерді бөліп алды:
шарт,оның құрамында көптеген аталған элементтер,байланыстар және олардың арасындағы қарым-қатынастар бар;
талап,ол есепті шешуге бағытталған нұсқау ретінде түсіндіріледі;
оператор,ол есептерді шешу үшін қойылатын талаптардың жиынтығы болып табылады.
Сондай-ақ, Ю.М.Колягин төртінші компонентті бөліп көрсетеді - есепті базис арқылы шешу,бұл есептің теориялық немесе практикалық негізі.
Ю.М.Колягин есептердің шығу тегін есептер жүйесінің пайда болуымен және қажетті жағдайда туындаған есептер жүйесінің мәселелерімен байланыстырады.
Фридманда есеп терминінің өзі белгілі бір проблемалық жағдайды сипаттайды,сондықтан да адамдарда есептерді шешу кезінде қандай да бір қиындықтар туындай ма,есептердің шешімін іздеу және оны жүзеге асыру ақыл-ой іс-әрекетіне күш түсіре ме деген сұрақтарды шешуде қолданылады. Ал Колягин: егер де берілген есептер адамдарға қиындық тудырмаса,
онда бұл тапсырмалар есеп болып табылмайды,-деп санайды.
Психологияда есепті қандай да бір субъектінің зерттеу объектісі ретінде қарастырады,мысалы,Г.А.Балл есеп ұғымы психологиялық әдебиетте 3 түрлі санатты объектіні түсіндіру үшін қолданылады деп атап өтті:

1) субъектінің алдына қойылған мақсаттардың категориясы ретінде;
2) сонымен қатар,қол жеткізілуі тиіс мақсаттардың категориясы ретінде;
3) ситуациялық жағдайды ауызша тұжырымдаудың категориясы ретінде. Психологиялық әдебиеттерде есеп терминін объектінің екінші санатты категориясы ретінде пайдалану кең таралған. Г.А.Балл есептерді шешуді анықтауды былайша түсіндірген: Жалпылама түрдегі есеп - бұл міндеттелген компоненттері бар жүйе болып табылады:
а) бастапқы жай-күйдегі есептер; б) жай-күйді талап ететін есептер.
А.К.Артемованың пікірі бойынша,есеп - бұл шарттары мен мақсаттары бар бірлік,егер осы компоненттердің біреуі болмаса,онда есеп те жоқ.Осыған байланысты,есептің шарттары орындалған жағдайда ғана есепті шешілді деп айтуға болады.
Ал В.И.Крупичтің пікірінше,мектептегі математикалық есептерді субъектінің материалдық формасына тәуелсіз күрделі объект ретінде қарастыруға болады.Бұл тәсіл есептердің ойлау субъектісінде болуы мүмкін екенін теріске шығармайды.Бұл жағдай оқушы берілген тапсырманы қабылдап,өзінің мүмкіндіктеріне сәйкес тапсырманы шешуге мақсат қойған жағдайда туындайды.
Н.Б.Истомина мәтінді есептерді шығарудың келесі кезеңдерін бөліп

көрсетеді:
есепті шешуге дайындық жұмысы;
мәтінді оқу және түсіну;
есептің шешілу жолдарын іздеу,жоспар құру;
есептің шешімін жазу;
шешілген есепті талдау.
Әр кезеңде мұғалім әр түрлі әдістемелік тәсілдерді пайдаланады. Есептерді шешудің әдістемелік тәсілдеріне шектеу қоюға болмайды. Өйткені,мұғалім оқыту процесінде есептерді шешу үшін өз әдіс-тәсілдерін қолданады.Нәтижесінде оның тиімділігіне көзі жетеді.
Сондықтан сабақты ұйымдастыра отыры п,оқушылардың білім-білік дағдыларын қалыптастырудың ең негізгі тәсілдерін ғана атайық:
алдыңғы әңгіме (фронтальді әңгіме);
көрнекі түсіндіру (қысқаша жазба,кесте,сызба,сурет және т.б.);
есептерді салыстыру (сұрақтар,мәтін,шешімдер);
есептерді түрлендіру (деректерді өзгерту);
жеткіліксіз және артық деректері бар мәтіндерді қарау;
оқушылармен бірге есептерді шешу;
есептерді басқа арифметикалық тәсілдермен шешу;
есептің шешімін тексеру;
есептерді саралау.
Бастауыш мектеп бағдарламасында оқушылар есептерді әр түрлі тәсілдермен шешуге үйренуі керек деп айтылады.
Есептерді әр түрлі тәсілдермен шешу дегеніміз не? Әдістемеде есептерді шешу тәсілдері төмендегідей:
арифметикалық;
алгебралық;
графикалық;
кестелік.
Есептердің қайсысын қай тәсілмен шешу керектігін орынды ажырата білу керек.Есептерді шешудің әр түрлі әдістері әр түрлі шешілу жолдарына әкеледі.
Есептерді әр түрлі тәсілдермен шешкеннен кейін, есептердің шешімдерін міндетті түрде салыстыру керек.Бұл тәсіл қай тәсілдің тиімді,қай тәсілдің артықшылығы бар екендігін көрсетеді.

ҚОЗҒАЛЫСҚА БЕРІЛГЕН ЕСЕПТЕРДІҢ НЕГІЗГІ ТҮРЛЕРІ

Бір пункттен екінші пунктке қарай бір бағыттағы қозғалысқа байланысты есептермен жұмыс
Қозғалысқа берілген есептердің негізгі түрлерінің бірі - бағыттас қозғалысқа тоқталайық.Бір пункттен екінші пунктке қарай бір бағыттағы қозғалысқа берілген есептерге артынан қуып жету қозғалысы және қалып қою қозғалысына берілген есептер жатады.Бағыттас қозғалыста екі дене қозғалысты бір мезгілде бастайтын болса,онда олар кездесетін жағдайда,екі дене қозғалыс басталғаннан кездескенге дейін бірдей уақыт жұмсайды.Ал,екі дене қозғалысты әр түрлі уақытта бастайтын болса,онда олар кездескенге дейін қозғалысты алғашқы бастағаны көбірек уақыт жұмсайды.Бір бағыттағы қозғалыс есептеріне мысалдар келтірейік.
Артынан қуып жету қозғалысына берілген есептер
Мысал №1.Мектеп пен үйдің арасындағы қашықтық 200 м.Бір мезгілде мектептен оқушы,ал үйден әжей шығып,олар бір бағытта жүрді.Оқушының жүру жылдамдығы 110 ммин,ал әжейдің жүру жылдамдығы 60 ммин.Қанша уақыттан кейін оқушы әжейді қуып жетеді?
110ммин 60ммин

Мектеп Үй

Оқушы Әжей
200 м
Есепті оқыған соң мәтін бойынша әңгіме жүргізіледі.Оқушылар сызбаны пайдаланып,есептің шартын құра бастайды.Мұғалім мәтін бойынша сұрақтар қоя отырып,есептің берілгенін талқылайды.
-Есепте не туралы айтылған? (Оқушы мен әжей туралы айтылған)
-Есепте не белгілі? (мектеп пен үйдің ара қашықтығы,оқушы мен әжейдің жүру жылдамдығы)
-Есептің сұрағы қандай? (Қанша уақыттан кейін оқушы әжейді қуып жетеді?)
-Есептің шартын құрамыз.
-Мектеп пен үйдің ара қашықтығы - S
-Оқушының жүру жылдамдығы - V1
-Әжейдің жүру жылдамдығы - V2
-Табу керек - T (қуып жету уақыты) Берілгені:
S=200 м
V1=110ммин V2=60ммин Табу керек: T - ?

Шешуі:
Оқушы мен әжейдің бір-біріне жақындау жылдамдығы - Vжақын. = V1 - V2 Vжақын.=V1 - V2=110 - 60 =50 ммин
Оқушы әжейді қуып жету үшін,екеуіні ң арасындағы бастапқы 200 м арақашықтықты жүріп өтуі керек.
T=S:Vжақын.=200:50=4 мин
Жауабы: Оқушы әжейді 4 минутта қуып жетеді.
Мысал №2.Мұрат пен Әлібектің үйлерінің арасы 160 м.Олар бір мезгілде үйлерінен мектепке қарай шықты.Әлібек 100 ммин жылдамдықпен,ал Мұрат Әлібектің артынан 120 ммин жылдамдықпен жүріп отырды.Неше минуттан кейін Мұрат Әлібекті қуып жетеді?
Мектеп
T - ? мин
V2=100ммин Ә.үйі
V1=120ммин М.үйі
160м
Есепті оқыған соң мәтін бойынша әңгіме жүргізіледі.Оқушылар сызбаны пайдаланып,есептің шартын құра бастайды.Мұғалім мәтін бойынша сұрақтар қоя отырып,есептің берілгенін талқылайды.
-Есепте не туралы айтылған? (Мұрат мен Әлібек туралы айтылған)
-Есепте не белгілі? (Мұрат пен Әлібектің үйлерінің арасы,олардың жүру жылдамдықтары)
-Есептің ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.