Есептерді шешу тәсілдері

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 27 бет
Таңдаулыға:

Қазақстан Республикасы Білім және ғылым министрлігі
Шығыс Қазақстан гуманитарлық колледжі

Қорғауға жіберілді
_____________2017 ж.

КУРСТЫҚ ЖҰМЫС

Тақырыбы: Мәтін есепті шығарудағы кескіндеу түрлері

0111000 Негізгі орта білім беру мамандығы бойынша

Орындаған 4-ИНФО-1
тобының студенті Н.Н. Мырзахметова

Ғылыми жетекшісі
_____________2017 ж. А.Ақылбек

Норма бақылаушы
_____________2017 ж. Ж.А.Слямбекова

Өскемен, 2017 ж.
Мазмұны

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .4
1. Есеп ұғымының ғылыми әдістемелік әдебиеттерде қарастырылуы ... ... ... ... 6
1.1 Есеп ұғымының негізі ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...6
1.2 Есептерді шешу тәсілдері ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..11
1.3 Мәтін есептерді шығарудағы кескіндеу түрлері ... ... ... ... ... ... ... ... ... ... ... ..12
2. Бастауыш сыныпта кескіндеу түрлерінің қолданылуы ... ... ... ... ... ... . ... ... ... 13
0.1 Есеп түрлері ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...13
2.2 Мәтін есептерді шығаруда кескіндеу түрлерін қолдану ... ... ... ... ... ... ... ... 18
3. Эксперимент жұмысының нәтижесі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..27
Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .32
Пайдаланылған әдебиеттер тізімі ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... 33

Кіріспе

Қазақстан Республикасының Президенті Н.Ә.Назарбаевтың Қазақстан халқына жолдауында: Білім беру реформасы - Қазақстанның бәсекеге нақтылы қабілеттілігін қамтамасыз етуге мүмкіндік беретін аса маңызды құралдардың бірі.
Бізге экономикалық және қоғамдық жаңару қажеттіліктеріне сай келетін осы заманғы білім беру жүйесі қажет.
Жоғарғы білім беру саласында техникалық білім беруді дамытуға ерекше назар аудара отырып, жоғары оқу орындары желісінде оңтайландыру жүргізілуге тиіс. Осы заманғы мемлекеттік менеджерлер даярлау үшін Мемлекеттік басқару академиясының негізінде шетелдік серіктестіктердің қатысуымен ең жоғары шығармашылық стандарттарға сәйкес келетін ұлттық басқару мектебі құрылуы қажет.
Білім беру жүйесін дамытуда ынталандыру мақсатында және сектор мен мемлекет арасындағы серіктестікті нығайту мемлекеттік жекеменшілік білім беруге кредиттер бөлу жүйесін жетілдіру қажет - делінген [6].
Ал, оның негізі бастауыш сыныпта қаланбақ. Осы орайда оқушыларды математика негізі болатын білімдер жүйесімен және ол білімдерді саналы түрде шығармашылықпен қолдана алудың іскерлігі мен дағдыларын берік қалыптастыру мен ой-өрісін дамыту болып табылады. Сондықтан да бастауыш мектепте мәтін есептер шығаруда кескін түрлерін пайдалану арқылы оқушылардың ой-өрісін дамыту көкейтесті мәселе.
Мектеп оқулықтарында мәтін есептерді шығаруға әдістемелік нұсқау жоқ десек те болады, көбінесе оқулықта бір немесе екі ғана шартпен берілетін қарапайым мәтін есептер үнемі қайталанып отырады. Осының әсерінен математиканың алдында тұрған негізгі талап - оқушылардың логикалық ойлау қабілеттерін дамыту, сонымен қатар математика пәнінде күнделікті өмірде кездесетін есептерді шығаруға үйрету, математикалық модель құра білу мәселелері назардан тыс қалуы мүмкін. Мәтін есептерді тура талқылауды керек ететін арифметикалық тәсілдерді қолдана отырып шығарудың оқушылардың логикасын дамытуда берері зор және арифметикалық тәсілді жақсы меңгерген оқушы мәтін есептерге жылдам, әрі дұрыс теңдеу құра алатыны сөзсіз[7].
Осы сараптамалардың негізінде біз курстық жұмыстың тақырыбын: "Бастауыш сыныптарда мәтін есептерді шығарудағы кескіндеу түрлері" деп алдық.
Зерттеу мақсаты: Кескіндеу түрлері арқылы мәтін есептерді шығарудың тиімді жолдарын анықтау.
Зерттеу міндеттері:
1. Ғылыми-теориялық әдебиеттерді қарастыру.
2. Негізгі ұғымдарға анықтама беру.
3. Мәтін есептерді шығарудағы кескіндеу түрлерін анықтау.
4. Мәтін есептерді шығарудағы кескіндеу түрлерінің тиімділігін анықтау.
Зерттеу объектісі: Бастауыш сынып оқушылары
Зерттеу пәні: Бастауыш сыныптардың математика сабақтарында мәтін есептерді шығару үрдісі.
Зерттеу болжамы: Егер мәтін есептерді шығаруда кескіндеу түрлері қолданылса, онда
1. Оқушылар мәтін есептерді шығарудағы білім сапасы артады
2. Оқушылар мәтін есептерді шапшаң шығаратын болады;
3. Оқушылардың мәтін есепке деген қызығушылықтары оянады.
Зерттеу әдіс-тәсілдері: Талдау, бақылау, эксперимент жұмысы, қорытындылау, салыстыру, сауалнама.

1. Есеп ұғымының ғылыми әдістемелік әдебиеттерде қарастырылуы

1.1 Есеп ұғымының негізі
Есеп адам өмірінде де, жалпы қоғамның өмір сүруі үшін де аса маңызды рөл атқарады. Себебі, жеке адамның өзіне-өзі, сондай-ақ оның күнделікті өмірде басқа адамдармен (және қоғам) өмірлік жағдайлар қоятын мәселелерді (есептерді) шешуге ақыл-ой иесі ретінде жеке тұлғаның бар қызметін, өмірлік және ойлау іс-әрекетін бағыттайды. Осы себептен, адамның өмірлік қызметі күн сайын мазмұны, рөлі, шешу үшін қолданылатын әдістері әр түрлі есептерді шешумен сипатталады деуге болады.
Адамның өндірістік және күнделікті тұрмыстық қызметі барысында туындайтын мәселелерді, сол сияқты таза математикалық және басқа да есептерді шешу проблемасы көптен бері зерттеліп келе жатқанымен, әлі күнге дейін есеп ұғымының көпшілікке ортақ келісілген анықтамасы жоқ. Бұл "есеп" терминінің кең мағыналығымен және бұл ұғымды жалпы түрде сипаттауға байланысты орын алып отырған объективті қиыншылықтармен түсіндіріледі. Кең мағынада "есеп" термининің әр алуан түрде, атап айтқанда, қандай да бір нәтижеге жетуді көздейтін алға қойылған мақсат, тапсырма, белгілі бір білімге және ойлануға негізделіп шешетін сұрақ; қандай да бір мәселе; жалпы білім беретін мектептердің барлық типтерінде, арнаулы орта және жоғарғы оқу орындарында оқытудың және білім мен практикалық дағдыларды оқытып-үйретудің және тексерудің әдісі ретінде қарастырылатыны белгілі. Орыс тілінің түсіндірме сөздігінде (С.И.Ожегов) "есеп" термині орындалуға, шешілуге тиісті, яғни, пайымдау, есептеу арқылы орындалатын жаттығу, ол зерттеуді және шешуді талап ететін күрделі ахуал деген анықтама берген [8]. Ғылымның әр саласында "есеп" терминінің өзіндік арнайы түсіндірмесі бар.
Мәселен, оқу процесіндегі "есеп" оқу мен еңбектегі оқушылардың танымдық және жаттығу белсенділіктерін арттыратын маңызды факторлардың бірі болып саналады. Сонда бұл термин оқушылардың анықталған мақсатты қабылдауын; қандай да бір сұраққа жауап алуға ұмтылудың қажеттігін; күткен нәтижеге жетудің керектігін; есепті шешу үшін берілген шарттар мен талаптардың ескерілуін; берілген мақсат пен шартқа сәйкес шешу тәсілдерінің немесе әдістерінің қолданылатынын сипаттайды [9]. Математиканы оқытуда "есеп" оқытудың мақсаты ретінде де, оқытудың құралы ретінде де қарастырылады. Оның көмегімен және оның негізінде негізгі ұғымдар қалыптастырылады, ұғымдардың жіктері тарқатылады, математикалық фактілердің нақты жағдайда қолданылуын көрсетеді және ол оқу, меңгеру қандай да білік қалыптастырудың объектісі ретінде көрініс табады, теория мен тәжірибенің арасын байланыстырушы қызметін атқарады, оқушылардың ойлауын дамытуға ықпал етеді. Математиканы оқытуда егер "есеп" термині кең мағынада түсіндірілсе, онда оған кез келген есептеу жаттығуларын, дәлелденуі анықталуға немесе зерттелуге тиісті кез келген теореманы, оқылатын математикалық ұғымдардың қандай да белгілерін анықтауды мақсат ететін және олардың ішінен осы ұғымды сипаттайтын кез келген тапсырмаларды немесе жаттығуларды және т.б. жатқызуға болады. Бұл жағдайда есп деп кәдімгі мектептегі есептерді, соның ішінде барлық мектеп оқулықтарындағы, мектеп емтихандарындағы, жоғары және арнаулы орта оқу орындарына түсу емтихандарындағы ұсынылып жүрген кейде мысалдар, жаттығулар, тапсырмалар деп аталатындарды айтуға болады. "Есеп" терминінің мұндай кең мағынадағы түсіндірмесі арнаулы және әдістемелік әдебиеттерде жиі кездеседі. Алайда, біздің ойымызша, "есеп " термині бастауыш мектепте математиканы оқытудың мақсаты мен ерекшеліктеріне үйлесетіндей "тарлау" мағынада анықталуы тиіс және орынды сияқты. Бұл тұрғыдан алғанда "есеп" терминінің мән-мағынасын анықтауға арналған жекелеген ұмтылыстар бар болғанымен, әдістемелік әдебиеттерде ол жеткілікті дәрежеде ашылмайды. Мәселен, көптеген әдістемелік еңбектерде (Бантова М.А., Пышкало А.М., Моро М.И., Истомина Н.Б., Лященко Е.И., Мазаник А.А., Колягин Ю.М., Столяр А.А., Дроздь В.А. және басқалар) арифметикалық мәтінді есептерді саралауға және оқыту барысындағы олардың мақсаты мен құралы ретіндегі ерекшеліктерін қарастыруға баса назар аударады. Бірақ, "мәтінді арифметикалық есеп" терминінің мән-мағынасы жете ашылмайды. М.А.Бантова бастаған авторлар "Бізді қоршаған өмірде санмен байланысты және оларға арифетикалық аамалдар орындауды талап ететін көптеген өмірлік жағдайлар туындайды, олар - есептер болып табылады", - деп түйіндейді. Сонда есептегі сан жиын элементтерінің санын немесе шаманың мәнін сипаттайды. Сондай-ақ, қатынасты немесе берілген дерексіз санды (дерексіз жағдайды қолданудың негізінде алынған) өрнектеп көрсетеді. Есеп шығару, математиканы оқытудың жалпы жүйесіндегі тиімді, нәтижелі жаттығулардың бірі болып саналады. Е.М.Лященко және А.А.Мазаник мәтін есептің танымдық функциясы бар, алайда математикалық қатынастың мән-мағынасы өмірлік тақырыбы мен математикалық емес тілдегі сөздің көлеңкесіндн қалып қоятын және де сонысымен оны шешуге қиындық тудыратын тапсырманың арнайы түрі ретінде қарастырады?. Сонымен бірге есептер математикалық фактілердің шынайы өмірдегі практикалық қолданысының мысалы болып табылатындығымен тиімді деп тұжырымдайды. А.А.Столяр мен В.Л.Дроздь тұрмыстық, табиғи мағынасы бар арифметикалық амалдың немесе амалдардың көмегімен шешілетін тапсырманы мәтінді есеп дейді [2]. Олардың пікірінше, мәтінді есептерді пайдаланатын тұрмыстық ұғым мен түсініктер оқушыларда алғашқы абстракция мен математикалық ұғымдарды қалыптастыру үшін бастапқы материал болып табылады. Сол сияқты оқушыларда математикалық ұғымдар мен қатынастар арқылы нақты өмірлік құбылысты байқауына мүмкіндік береді; қандай да түрдегі математикалық есепті шешу оны шешудің жалпы әдісін, белгілі бір ақыл-ой білігінің және танымдық операцияның қалыптасуына мүмкіндік береді; оларды (есептерді) шешудің маңызды дүниетанымдық мәні бар және адамгершілік сапалардың қалыптасуына негіз болатындай қоршаған шындықтың құбылыстарымен танысуға жол ашылады. Ал, А.М.Пышкало және Л.П.Стойлова мәтінді есепті белгілі бір жағдайдың (жағдайлардың) нақты компонентін сандық тұрғыдан сипаттау, сондай-ақ компоненттердің арасындағы қатынастардың бар немесе жоқ екендігін тағайындау немесе осы қатынастың түрін анықтау талабын қамтитын табиғи тілдегі баяндалуы ретінде анықтайды [2; 48-51].
Есеп дегеніміз - өмірде кездесетін жағдайдың (ситуацияның) сан ретіндегі сипаттамасын табуды талап ететін қарапайым тілде берілген сөйлем. Кез келген есеп екі бөлімнен тұрады: 1) есептің шарты; 2) есептің сұрағы. Есептің шартында қандай да бір жағдай, ондағы белгілі және белгісіз сан мәліметтер туралы айтылады. Белгілі және белгісіз сан мәліметтер айтылады. Белгілі және белгісіз сан мәліметтер арасындағы байланыстар "артық", "кем", "есе артық", "есе кем", т.с.с. қатынастар түрінде беріледі. Есептің сұрағында (немесе талабында) нені табу керек екендігі талап етіледі. Есептің сұрағы сұраулы сөйлем немесе бұйрықты сөйлем түрінде беріледі.
Мысалы, "үшбұрыштың ауданы нешеге тең?" сұраулы сөйлем түрінде, ал "үшбұрыштың ауданын тап" десе бұйрықты сөйлем түрінде беріледі.
Есеп - математикада кездесетін жаттығулардың ішіндегі ерекше түрі. Есепті басқа жаттығулардан айыру үшін оның өзіне ғана тән мәнді белгілерін білу керек. Ол мәнді белгілер мынадай:
1. Табиғи тілде тұжырымдалған мәтіннің көмегімен берілуі.
2. Мәтінде белгілі бір өмірлік жағдайдың сипатталуы.
3. Мәтінде міндетті түрде сұрақтың болуы.
4. Талап етілген сұраққа жауап беру үшін міндетті түрде ең болмағанда бір арифметикалық амалды орындалуы.
Егер аталған мәнді белгілердің ең болмағанда біреуі болмасы, онда мұндай жаттығулар есеп бола алмайды.
Мысалы, "Бір жұмыртқа 5 минутта піседі. Осындай 4 жұмыртқа неше минутта піседі? "деген тапсырма есеп болмайды. Мұнда есептің мәнді белгілерінің барлығы да бар сияқты болып көрінеді, бірақ есеп сұрағына жауап беру үшін арифметикалық амал орындалмайды.
Өмірде есептің сан алуан түрлері кездеседі. Кейбір кездерде есептің шарты мен сұрағы бірігіп кететін есептер де бар. Мысалы, жоғарыда тұжырымдалмаған есепті мынадай түрде өзгертуге болады:
" Токарь 2 сағатта 89 деталь, ал жұмыс аяғына дейін қалған уақытта бұдан 6 есе артық деталь дайындалса, онда бір күнде неше деталь дайындайды?" Мұнда есептің шартының бір бөлігі есеп сұрағымен бірігіп, "егер жұмыс аяғына дейін қалған уақытта бұдан 6 есе артық деталь дайындалса, онда ол бір күнде неше деталь дайындайды" деген бір сөйлеммен тұжырымдалған.
Сондай-ақ есеп сұрағына жауап беру кезінде ешқандай қатысы жоқ мәліметтерді артық берілген есептер де кездеседі. Мысалы, "Ералыда 10 қызыл асық және 5 көк асық бар, ал Ернарда 7 қызыл асық бар. Балаларда барлығы неше қызыл асық бар?"деген есепте 5 көк асық туралы мәлімет артық. Өйткені есеп сұрағына жауап беру кезінде бұл сан мәлімет қолданылмайды. Сонымен қатар кейбір есептерде есеп сұрағына жауап беру үшін сан мәліметтерді жеткіліксіз болатын жағдайлар да болады. Мұндай есептерді сан мәліметтері жеткіліксіз деп атайды. Ондай есептерді шешу үшін жетіспейтін сан мәліметті есепті шешуші адамның таңдап алуына болады. Мысалы, "Тіктөртбұрыштың ұзындығы енінен 2 есе артық, тіктөртбұрыштың ауданын тап". Бұл есепте тіктөртбұрыштың ені туралы мәлімет жеткіліксіз. Сондықтан есептің сұрағына жауап беру мүмкін емес. Бірақ ені туралы сан мәліметті есепті шешуші адам өзі таңдап алып, есеп мазмұнына енгізсе, онда қойылған сұраққа жауап беруге болады. [1. 88-90]
Есеп - бірдеңенің болуын анықтау, оның заттай және ақшалай тұлғада өлшенуі, сандық және сапалық жағынан тіркелуі; басқарылатын нысанның жай-күйі, оның айналысы, басқарушылық өкімдерінің орындалуы және қорытындылаушы мәліметтер туралы деректердің жиынтығы болып табылатын қажетті ақпаратты жинау мен тіркеу жүйесі.
Есеп шаруашылық қызмет пен қоғамдық өмірдің түрлі аялары туралы тұрақты ақпаратты қамтамасыз етеді. Қоғамның (мемлекеттің, ұйымның) өндіргіш күштерінің дамуына байланысты есептік ақпараттың көлемі мен оның басқару ісіндегі рөлі арта түседі. Есеп бухгалтерлік, статистикалық және оралымды түрлерді біріктіретін бірыңғай жүйе болып табылады. Есеп негізі 1-сыныпта енгізіледі[3].

1.2 Есепті шешу тәсілдері
Кез-келген есеп оны шешуді талап етеді, яғни есеп сұрағына жауап берілуі тиіс. Есепті шешеу дегеніміз - мәтінді берілген белгілі және ізделіндә сан мәліметтер арасындағы байланысты тағайындап, керекті амалдарды орындау арқылы есеп сұрағына жауап беру.
Есепті шешу процесінің мынадай міндетті кезеңдері болуы тиіс:
1. Есеп мазмұнымен танысу. Есеп мащмұнымен танысу дегеніміз - есепте баяндалған жағдайды жалпы түрде түсіну, есеп шартын, талабын, яғни сұрақтары, барлық терминдері және берілгендерді түсіну, бір сөзбен айтқанда есеп мазмұнын меңгеру.
2. Есептің шешімін іздестіру. Мұнда есепті шешу жоспары құрастырылады, есеп мазмұнында баяндалған қандай да нақты жағдайға сәйкескелетін арифметикалық амалдардың рет-тәртібін логикалық тұрғыда анықтау және негіздеу.
3. Есеп шешу жоспарын жүзеге асыру, яғни таңдалып алынған амалдарды орындау арқылы есеп сұрағына жауап беру.
4. Есептің шешуін тексеру, яғни алынған жауаптың дұрыс екендігіне көз жеткізу.
Толық шығарылған есеп осы кезеңдердің барлығын да қамтиды. Бірақ бұл кезеңдер есепті шешу барысындаерекше бөлініп көрсетілмейді.
Есепті шешу тәсілң негізінен арифметикалық және алгебралық болып бөлінеді.
Есепті арифметикалық тәсілмен шешкенде есеп сұрағына жауап сандар мен шамаларға арифметикалық амалдар орындаудың нәтижесінде табылады. Және де бір есепті бірнеше арифметикалық әдіспен шешуге болады. Егер есепті шешу негізіне алынған белгілі мәліметтер мен ізделіндінің байланысы бір-бірінен өзгеше болса, сонда және тек сонда есеп әр түрлі әдіспен шешілді деп айтуға болады.
Есепті алгебралық тәсілмен шешкенде есеп сұрағына жауап беру үшін, есеп мазмұнына сәйкес теңдеу құрылады және сол теңдеуді шешу арқылы есеп сұрағына жауап береміз. Есептң алгебралық тәсілмен шешудің де әр түрлі әдісі болуы мүмкін. Егер бір ғана есептің мазмұнына сәйкес әр түрлі теңдеулер құрылса, онда есепті әр түрлі алгебралық әдіспен шештік деп айтуға болады.
Есептерді шешудің қарастырылған тәсілдерден басқа да тәсілдері бар: графикалық және практикалық.
Есепті графикалық тәсілмен шешкенде есеп мазмұнына сәйкес сызбалар салынады, кесінділер тұрғызылады. Сызбалардың орналасуына қарап және кесінділердің ұзындықтарын өлшеу арқылы есеп сұрағына жауап береміз.
Есепті практикалық тәсілмен шешкенде есеп мазмұнына сәйкес заттарға амалдар қолданылады. Зат ретінде түрлі санау материалдарын (таяқшалар, дөңгелекшелер, т.б.) қолданамыз.

1.3 Мәтін есептерді шығарудағы кескіндеу түрлері
Есепті иллюстрациялау- есепке енетін шамаларды, берілген және ізделіп отырған сандарды мүшелерге бөлу үшін, сондай - ақ олардың арасындағы байланысты тағайындау үшін көрнекілік құралын пайдалану.
График түріндегі иллюстрация. Бұл кесінді түріндегі иллюстрация (шамалар ұзындық бірліктерімен немесе шамалар арасындағы қатынастар берілген есептерді).
Заттық иллюстрация . Иллюстрация ретінде есепте сөз болып отырған не нәрселердің өзі немесе олардың суреттері пайдаланылады.
Схемалық иллюстрация. Шамалар, сандар (деректер мен ізделінді) және олардың арасындағы байланысты қолайлы түрде көрсетуге болатын есептің қысқаша жазылуы
Иллюстрация нәрсе түрінде немесе сызба түрінде болуы мүмкін.
Бірінші жағдайда иллюстрация ретінде есепте сөз болып отырған не нәрселердің өзі немесе олардың суреттерін пайдалану мүмкін, солардың көмегімен заттардың тиісті амалдары иллюстрацияланады.

2. Бастауыш сыныпта кескіндеу түрлерінің қолданылуы

2.1 Есеп түрлері
Барлық арифметикалық есептер, оларды шешу үшін орындалатын амалдар санына қарай, жай есептерге және құрама есептерге бөлінеді.
Бір ғана амалмен орындалатын есеп жай есеп деп аталады. Шығару үшін өзара байланысты бірнеше амал орындалатын есеп құрама есеп деп аталады.
Жай есептерді, не оларды шығару үшін қолданылатын амалдарға (қосу, азайту, көбейту, бөлу амалымен шығарылатын жай есептер), немесе оларды шығару үстінде қалыптасатын түсініктерге байланысты түрлерге бөлуге болады.
1-сыныпта жай есептің 6 түрі қарастырылады:
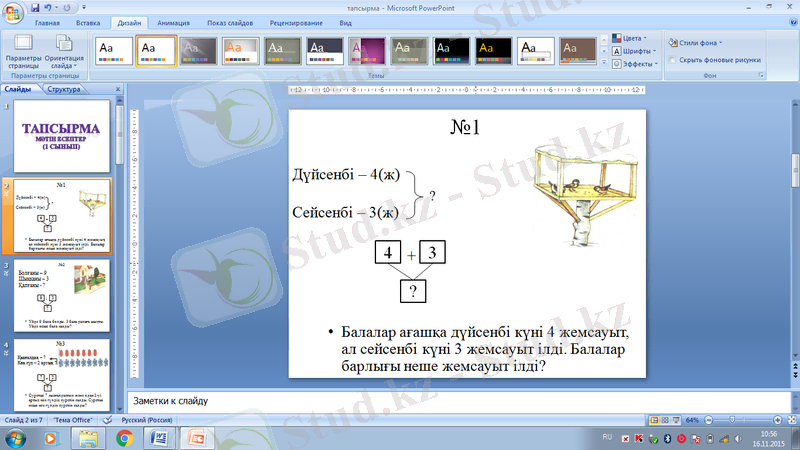
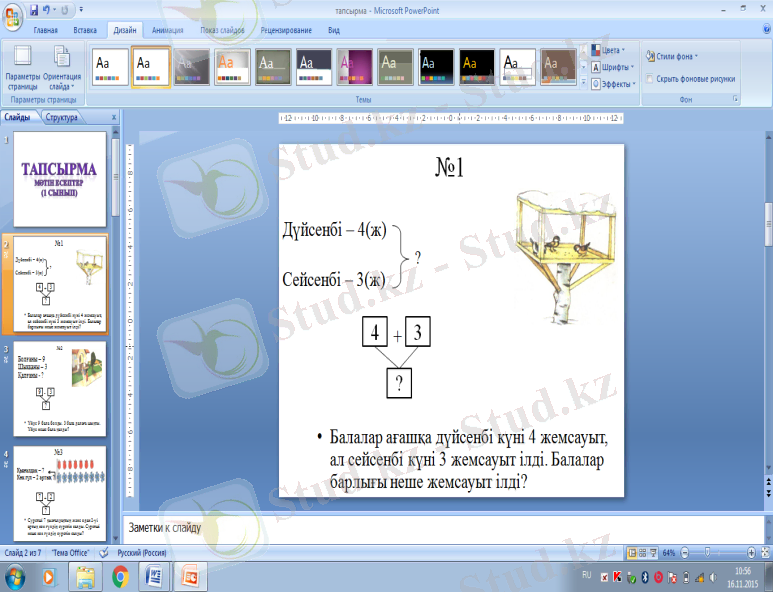
1. Екі санның қосындысын табу.
Мысалы: Балалар ағашқа дүйсенбі күні 4 жемсауыт, ал сейсенбі күні 3 жемсауыт ілді. Балалар барлығы неше жемсауыт ілді?

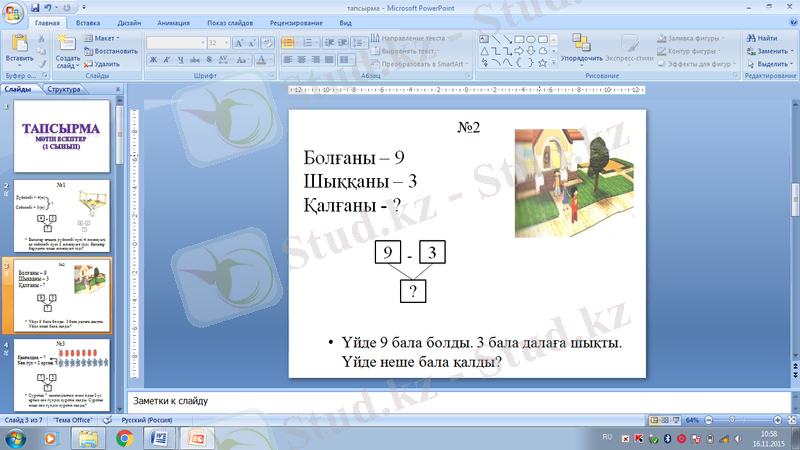
2. Қалдықты табу.
Мысалы: Үйде 9 бала болды. 3 бала далаға шықты. Үйде неше бала қалды?

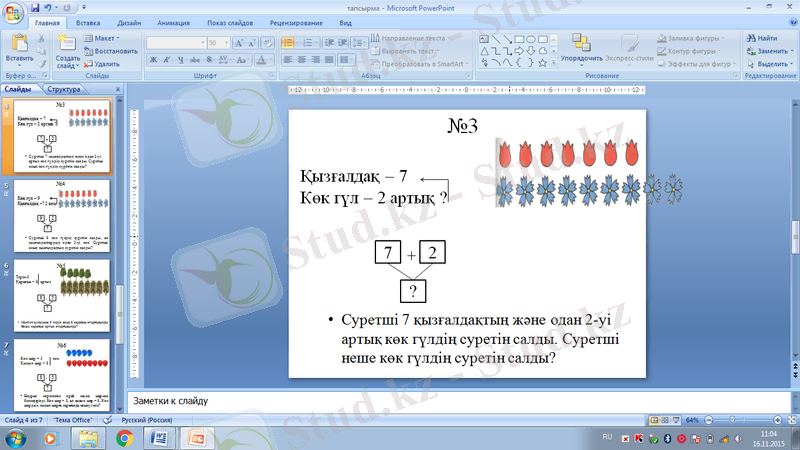
3. Сандарды бірнеше бірлікке арттыруға арналған есептер.
Мысалы: Суретші 7 қызғалдақтың және одан 2-уі артық көк гүлдің суретін салды. Суретші неше көк гүлдің суретін салды?

4. Сандарды бірнеше бірлікке кемітуге арналған есептер.
Мысалы: Суретші 9 көк гүлдің суретін салды, ал қызғалдақтардың одан 2-уі кем. Суретші неше қызғалдақтың суретін салды?

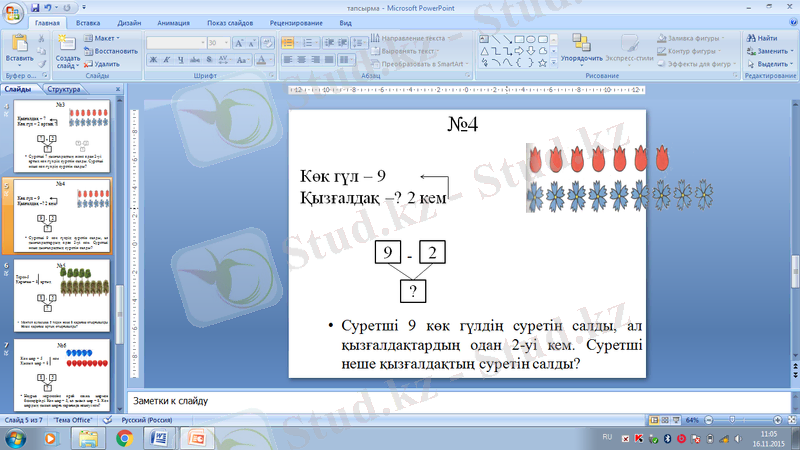
5,6. Айырмалық салыстырудың екі түріне берілген есептер.
Мысалы: 5. Мектеп ауласына 5 терек және 8 қарағаш отырғызылды. Неше қарағаш артық отырғызылды?

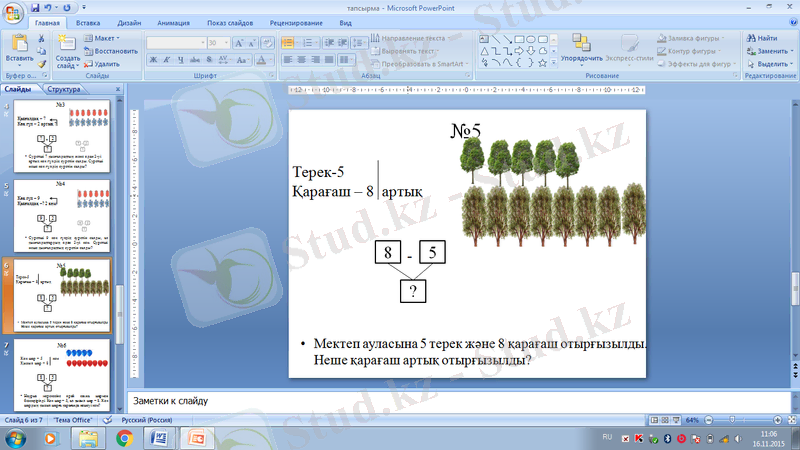
Мысалы: 6. Наурыз мерекесіне орай сахна шармен безендірілді. Көк шар - 5, ал қызыл шар - 8. Көк шардың қызыл шарға қарағанда нешеуі кем?

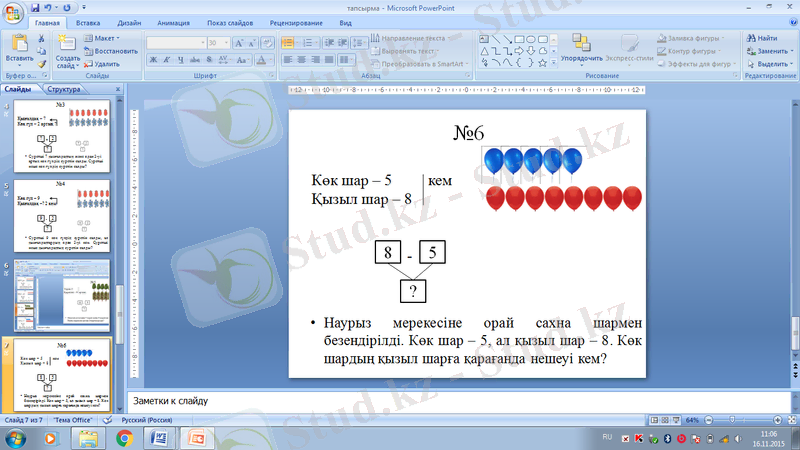
Жай есептердің топтары:
1-топ. Арифметтикалық амалдардың нақты мәнін ашатын есептер:
1. Екі санның қосындысын табу
2. Қалдық табу
3. Бірдей қосылғыштардың қосындысын(көбейтіндісін) табу
4. Тең бөліктерге бөлу
5. Тиісінше бөлу
2-топ. Арифметикалық амалдардың компоненттері мен нәтижелері арасындағы байланысты есептер.
1. Берілген қосындымен екінші қосылғыш бойынша бірінші қосылғышты табу. Мысалы: Қыз бала бірнеше шұңғыл және 2 майда тәрелке жуды. Барлығы 5 тәрелке жуды. Қыз бала қанша шұңғыл тәрелке жуды. 5-2꞊3(тәрелке)
2. Белгілі қосындымен белгілі қосылғыш бойынша екінші қосылғышты табу. Мысалы: Қыз бала 3 шұңғыл және бірнеше майда тәрелке жуды. Барлығы 5 тәрелке жуды. Қыз бала қанша майда тәрелке жуды. 5-3꞊2(тәрелке)
3. Белгілі азайтқышпен айырма бойынша азайғышты табу. Мысалы: балалар 3 ұяны ағаш басына іліп қойғанда тағы ұя қалды. Балалар барлығы қанша ұя жасаған? 3+4꞊7(ұя)
4. Белгілі азайғыш пен айырма бойынша азайтқышты табу. Мысалы: Балалар барлығы 6 ұя жасады. Оның бірнешеуін ілгеннен кейін тағы 4 ұя қалды. Қанша ұя ілінді? 6-4꞊2
5. Белгілі көбейтінді мен екінші көбейткіш бойынша бірінші көбейткішті табу. Мысалы: Тіктөрт
6. Белгілі көбейтінді мен бірінші көбейткіш бойынша екінші көбейткішті табу.Мысалы:
7. Белгілі бөлгіш пен бөлінді бойынша бөлінгішті табу. Мысалы:
8. Белгілі бөлінгіш пен бөлінді бойынша бөлгішті табу. Мысалы:
3-топ. Арифметикалық амалдардың жаңа мағыналарын ашатын есептер. 2-ге бөлінеді:
oo Айырма ұғымына
oo Қатынас ұғымына
Айырма ұғымына байланысты:
1. Сандарды айырмалық салыстыру (Бірінші түрі)
Дәптер 7 теңге, ал өшіргіш 3 теңге тұрады. Дәптер өшіргіштен неше теңгеге қымбат? 7-3꞊4 теңге
2. Санды айырмалық салыстыру (Екінші түрі)
Дәптер 7 теңге, ал өшіргіш 3 теңге тұрады. Өшіргіш дәптерден неше теңгеге арзан ? 7-3꞊4 теңге
3. Сандарды бірнеше бірлікке арттыру (тура формасы)
Лақтың салмағы 7 киллограм, ал қозының салмағы одан 3 киллограмға артық. Қозының салмағы неше киллограм? 7+3꞊10
4. Сандарды бірнеше бірлікке арттыру (жанама формасы)
Лақтың салмағы 7 киллограм, бұл қозының салмағынан 3 киллограмға кем. Қозының салмағы неше киллограм? 7+3꞊10
5. Сандарды бірнеше бірлікке кеміту (тура формасы)
Аққу 88 км ұшты, ал көгершін одан 26 км кем ұшты. Көгершін неше км ұшты? 88-26꞊62
6. Сандарды бірнеше бірлікке кеміту (жанама формасы)
Аққу 88 км ұшты, бұл көгершіннің ұшқанынан 26 км артық. Көгершін неше км ұшты? 88-26꞊62
Қатынас ұғымына байланысты:
1. Сандарды еселік салыстыру немесе екі санның қатынасын табу
1) Бақта 10 терек және 5 шырша өсіп тұр. Бақтағы терек шыршадан неше есе артық? 10:5꞊2
2) Домбыра үйірмесіне 8 ұл және 4 қыз бала қатысады. Қыз балалар ұл балаларға қарағанда неше есе кем? 8:4꞊2
2. Санды бірнеше есе арттыру
Тура формасы: Бүркіт 30 жыл, ал тасбақа одан 10 есе артық өмір ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.