Тригонометриялық теңсіздіктерді шешудің негізгі әдістері


Тыңдаушының өзіндік жұмысы
Тақырыбы: Тригонометриялық теңсіздіктерді шешу әдістері
Орындаған: Эшанова Султоной Абитдиновна
Түркістан облысы, Кентау ҚББ, «Ескі Иқан ЖОМ»
Жоспар
- Кіріспе
- Негізгі бөлім
Тригонометриялық теңсіздіктерді шешудің негізгі әдістері
- Қарапайым тригонометриялық теңдеулерді шеші
- Графикалық әдіс
- Алгебралық әдіс
- Қорытынды
- Қолданылған әдебиеттер тізімі
- Кіріспе
Өзектілігі. Тарихи тұрғыдан тригонометриялық теңдеулер мен теңсіздіктер мектеп курсында ерекше орын алды. Тригонометрия мектеп курсының және жалпы математика ғылымының маңызды бөлімдерінің бірі деп айта аламыз.
Тригонометриялық теңдеулер мен теңсіздіктер орта мектеп математикасы курсында оқу материалының мазмұнында да, оларды зерттеуде қалыптасатын және жасалуы керек теориялық және қолданбалы есептердің көптеген мәселелерін шешуге қолданылатын және жасалуы тиіс оқу-танымдық іс-әрекет әдістерінде де негізгі орындардың бірін алады.
Тригонометриялық теңдеулер мен теңсіздіктерді шешу тригонометрия бойынша барлық оқу материалдарына қатысты студенттердің білімін жүйелеуге алғышарттар жасайды (мысалы, тригонометриялық функциялардың қасиеттері, тригонометриялық өрнектерді түрлендіру әдістері және т. б. ) және зерттелетін материалмен алгебрада (теңдеулер, теңдеулер, теңсіздіктер, алгебралық өрнектердің бірдей түрлендірулері және т. б. ) .
Басқаша айтқанда, тригонометриялық теңдеулер мен теңсіздіктерді шешу әдістерін қарастыру осы дағдыларды жаңа мазмұнға ауыстырудың түрін қарастырады.
Теорияның маңыздылығы және оның көптеген қолданбалары таңдалған тақырыптың өзектілігін дәлелдейді. Бұл өз кезегінде курстық жұмыстың мақсатын, міндеттерін және зерттеу тақырыбын анықтауға мүмкіндік береді.
Зерттеу мақсаты: тригонометриялық теңсіздіктердің қол жетімді түрлерін, оларды шешудің негізгі және арнайы әдістерін жалпылау, мектеп оқушыларының тригонометриялық теңсіздіктерді шешуге арналған тапсырмалар жиынтығын таңдау.
Зерттеу мақсаты:
- Зерттеу тақырыбы бойынша қол жетімді әдебиеттерді талдау негізінде материалды жүйелеу.
- «Тригонометриялық теңсіздіктер» тақырыбын бекітуге қажетті тапсырмалар жиынтығын беріңіз.
- Зерттеу нысаны - мектеп математикасының курсында тригонометриялық теңсіздіктер.
- Зерттеу пәні: тригонометриялық теңсіздік түрлері және оларды шешу әдістері.
- Теориялық маңыздылығы материалды жүйелеуде жатыр.
- Практикалық маңыздылығы: теориялық білімді есептер шығаруда қолдану; тригонометриялық теңсіздіктерді шешудің негізгі жалпы әдістерін талдау.
- Зерттеу әдістері: ғылыми әдебиеттерді талдау, алынған білімді синтездеу және жалпылау, есептер шығаруды талдау, теңсіздіктерді шешудің оңтайлы әдістерін іздеу.
2. Тригонометриялық теңсіздіктерді шешудің негізгі әдістері
- Қарапайым тригонометриялық теңсіздіктерді шешу
Тригонометриялық теңсіздікті шешу дегеніміз теңсіздікті қанағаттандыратын, теңсіздікке кіретін белгісіз шамалардың жиынтығын табуды білдіреді.
Тригонометриялық теңсіздіктердің негізгі бөлігі оларды қарапайым түрге келтіру арқылы шешіледі:
- (,, ),
- (,, ),
- (,, ),
- (,, ) .
1. Бірлік шеңберде x санының синусының анықтамасын қолданыңыз.
2. Бірлік шеңбер салыңыз,
3. Ординаталар осінде координатасы a болатын нүктені белгілеңіз.
4. Сол нүктеден ОХ осіне параллель түзу жүргізіңіз және оның шеңбермен қиылысу нүктесін белгілеңіз.
5. Ординасы a нүктесінен кіші болатын барлық нүктелерді қамтитын шеңбердің доғасын белгілеңіз.
6. Жүріп өту бағытын көрсетіңіз (сағат тіліне қарсы), аралықтың соңына функцияның периоды болатын 2πn ,
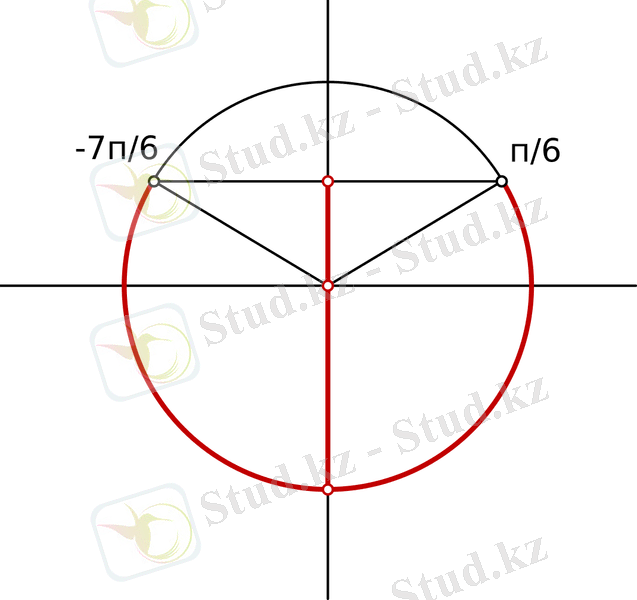
1 - есеп . Теңсіздікті шешіңіз:
Бірлік шеңберде шеңберді А жіне В нүктелерін қиятын
NM аралығындағы y тің барлық мәндері
1
0, 5
-0, 5
-1
-3
-2
-1
1
2
3
0
π
6
13
π
6
5
π
6
-7
π
6
;
;
y=
1
2
1
N
M
A
B
Сонымен,
яғни
Жауабы:
2. 2. Графикалық әдіс
Практикада тригонометриялық теңсіздіктерді шешудің графикалық әдісі көбінесе пайдалы болып келеді. Осы әдістің болмысын
1. Егер аргумент- күрделі ( х тен өзге ) болса, онда оны t айнымалысына ауыстырамыз.
2. Бір координаталар жүйесінде tOy жазықтығында
3. Синусоида
4. Косинустың периодын ескере отырып t аргументі үшін қос теңсіздік жазамыз.
5. Айнымалыға кері ауыстыру қолданамыз (бастапқы аргументке қайтамыз) және қос теңсіздіктегі х тің мәнін өрнектейміз, жауабын сан аралығында жазамыз.
2 -есеп. Теңсіздікті шешіңдер:
Теңсіздіктерді графикалық әдіспен шешкен кезде функцияның графиктерін мейлінше анық сызу керек. Теңсіздікті түрлендіреміз:
Бір координаталар жүйесінде
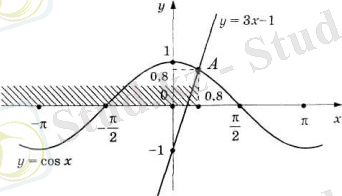
Функциялардың графиктері координаталары
Жауабы:
2. 3. Алгебралық әдіс
Көбінесе тригонометриялық теңсіздіктерді сәтті таңдалған жолмен оны алгебралық (рационал немесе иррационал) теңсіздікке келтіруге болады. Осы әдістің астарында теңсіздікті түрлендіру, жаңа айнымалы еңгізу назарда тұтылады. Осы әдістің қолдануын белгілі бір есептерде қарастырайық.
3-есеп.
\[\sin x\cos{\frac{p}{6}}-\cos x\sin{\frac{\pi}{6}}\leq0,5\]
\[\sin{\frac{\Phi}{\mathfrak{G}}}x-{\frac{\pi}{6}}{\frac{\mathfrak{G}}{\mathfrak{\phi}}}\leq0,5\]
Жауабы :
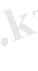
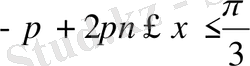 ,
,
Қорытынды
Зерттеудің барлық міндеттері орындалды. Теориялық материалдар жүйеленген: тригонометриялық теңсіздіктің негізгі түрлері мен оларды шешу әдістері (графикалық, алгебралық) қарастырылған. Әрбір әдіске есеп келтірілген. Теориялық бөлім артынан практикалық бөлім жүріп отырды.
Осы зерттеу жұмысын оқушылар өзіндік жұмыс ретінде қолдануларына болады. Мектеп оқушылары өздерінің осы тақырыпты қандай меңгергендерін қадағалап, әр түрлі қиындықтағы есептерді шығарып жаттығуына болады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz