Айналу беттері

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 11 бет
Таңдаулыға:

Реферат

«Көпжақтар және көпжақтарды кескіндеу. Айналу беттері. Винттік беттер. Кеңістік қисық сызықтар»

Орындаған:

Тобы:

Қабылдаған:

Жоспар:

Кіріспе
Көпжақтар жайлы негізгі түсініктер
Көпжақтардың түрлері
Дұрыс көпжақтардың тарихы
Көпжақтарды кескіндеу
Айналу беттері туралы мәлімет
Винттік беттер тақырыбындағы негізгі ұғымдар
Кеңістік қисық сызықтар
Пайдаланылған әдебиеттер

Кіріспе

«Көпжақтар» тақырыбы - мектеп геометриясының дәстүрлі курсының негізгі тақырыптарының бірі. Олар стереометрияның негізгі тақырыбын құрайды. Параллель және перпендикуляр түзулер мен жазықтықтарды, дифференциалдық бұрыштарды және басқаларды зерттеу, сондай-ақ векторлар мен координаталарды енгізу - мұның бәрі стереометрияның бастамасы, оның неғұрлым маңызды нысандарын - негізінен денелер мен беттерді зерттеу үшін құралдарды дайындау. Сонымен қатар, полихедралардың өзі көптеген қызықты қасиеттері бар барлық денелерден ерекшеленетін, әсіресе теоремалар мен проблемалармен ерекшеленетін өте маңызды зерттеу нысаны болып табылады. Мысалы, сіз Эйлер теоремасын тұлғалардың, шеттердің және шеттердің саны туралы еске түсіре аласыз, кәдімгі полифедралардың симметриясы, кеңістікті полифедралармен толтыру туралы сұрақтар және т. б. Көпжақтарға мектеп бағдарламасында көбірек көңіл бөлу керек, өйткені олар кеңістіктік бейнелерді дамыту үшін, сонымен қатар геометрияның мәнін құрайтын тірі кеңістіктік қиялдың үйлесімділігін қатаң логикамен үйлестіруді дамыту үшін өте бай материал береді. Тіпті полиэдрге қатысты қарапайым фактілер де мұндай байланысты қажет етеді, сондықтан бұл оңай емес. Параллелепипедтің диагональдарының бір нүктеде қиылысуы сияқты қарапайым факт болса, оны дәл көру үшін қиялдың күш-жігерін талап етеді және қатаң дәлелдеуді қажет етеді.

Көпжақтарға модельдерді жасау барысында студенттер теориялық білім мен дағдылардан басқа, қалыптасқан жаңа тұжырымдамаларды сызбаның көмегімен және құрылыс мәселелерінің нақты шешімдерімен біріктіреді. Модельдердің тәуелсіз өндірісінде кескіндер бөліктерге жасалады, сондықтан олармен түрлі манипуляциялар жасауға болады. Сонымен қатар, олардың барлық қасиеттері мен ерекшеліктері студенттердің жадында оңай сақталады.

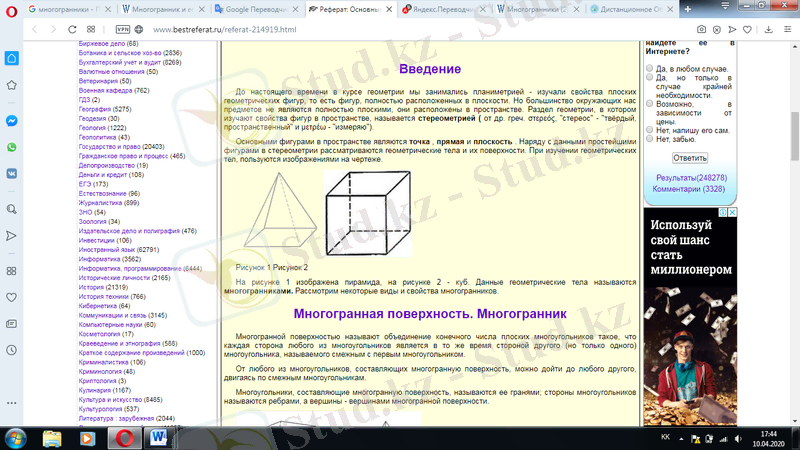Қазіргі уақытқа дейін геометрия курсында біз планиметриямен айналыстық-жазық геометриялық фигуралардың, яғни жазықтықта толық орналасқан фигуралардың қасиеттерін зерттадық. Бірақ бізді қоршаған заттардың көпшілігі тегіс емес, олар кеңістікте орналасқан. Кеңістіктегі фигуралардың қасиеттерін зерттейтін геометрия бөлімі стереометрия деп аталады. στερεός, "стереос" - "қатты, кеңістіктік" және μετρέω - "өлшеу") . Кеңістіктегі негізгі фигуралар нүкте, түзу және жазық болып табылады . Стереометриядағы қарапайым фигуралармен қатар геометриялық денелер мен олардың беттері қарастырылады. Геометриялық денелерді оқу кезінде сызбада суреттерді пайдаланады.

1-суретте пирамида, 2-сурет - текше көрсетілген. Бұл геометриялық денелер көпжақтар деп аталады. Көпжақтардың кейбір түрлері мен қасиеттерін қарастырыңыз.

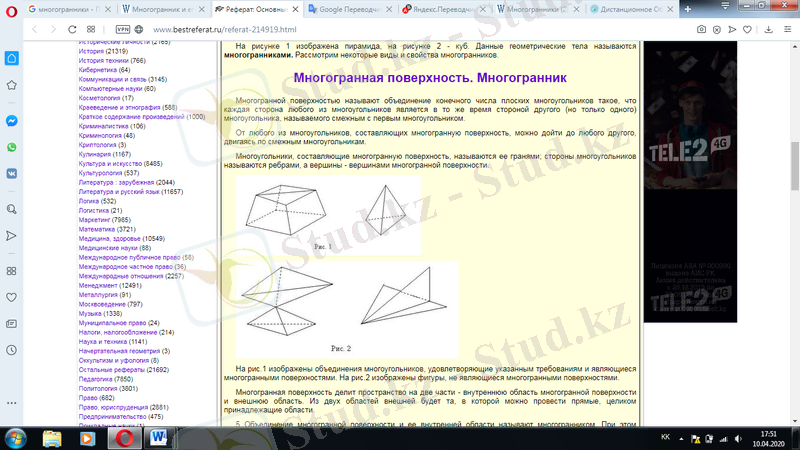
Көп қырлы бет болып жазық көпбұрыштардың соңғы санының бірігуі көпбұрыштардың әрбір жағы сол уақытта бірінші көпбұрышпен аралас деп аталатын басқа (бірақ бір ғана) көпбұрыштың жағы болып табылады. Көп қырлы бетті құрайтын кез келген көпбұрыштардан аралас көпбұрыштармен қозғала отырып, кез келген басқа жерге жетуге болады. Көп қырлы беттерді құрайтын көпбұрыштар оның қырлары деп аталады; көпбұрыштардың жақтары қырлар деп аталады, ал биіктіктері көп қырлы беттердің биіктіктері деп аталады.

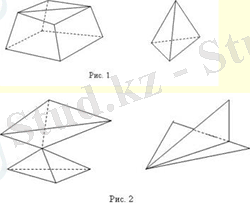
1-суретте көрсетілген талаптарды қанағаттандыратын және көп қырлы беттер болып табылатын көпбұрыштардың біріктірулері бейнеленген. 2-суретте көп қырлы бет болып табылмайтын фигуралар бейнеленген. Көп қырлы бет кеңістікті екі бөлікке бөледі - көп қырлы беттің ішкі аймағы және сыртқы аймақ. Екі облыс сыртынан тікелей, тұтастай облыстарға тиесілі болатындай болады. Көп қырлы бетті және оның ішкі аймағын біріктіру көп қырлы деп аталады. Бұл ретте көп қырлы бет пен оның ішкі аймағы көп қырлы бет пен ішкі аймақ деп аталады. Көп қырлы беттердің қырлары, қабырғалары мен жоғарғы жағы тиісінше қырлары, қырлары мен шыңдары деп аталады.

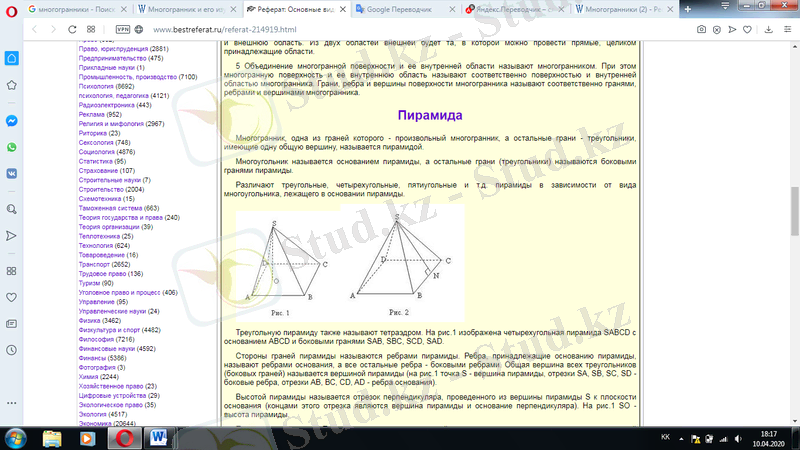
Пирамида. Көпжақтардың ерекше қызықты түрінің бірі - пирамида. Пирамида тақырыбын қозғағанда Мысыр пирамидаларын атамай кету мүмкін емес. Олар тек математиктерді ғана емес, сонымен қатар физиктерді, тарихшыларды, т. б. қызықтырып келеді. Пирамида деп бір жағы кез келген көпбұрыш, ал қалған жақтары төбелері ортақ үшбұрыштардан тұратын көпжақты атайды. Пирамидаларды дөңес және дөңес емес деп бөлеміз. Пирамиданың биіктігі дегеніміз - оның төбесінен табан жазықтығына түсірілген перпендикуляр немесе осы перпендикулярдың ұзындығы. Егер пирамида табаны дұрыс көпбұрыш болып, төбесінің проекциясы табанының центріне дәл түссе, онда ол дұрыс пирамида деп аталады. Дұрыс пирамиданың бүйір жағының пирамида төбесінен түсірілген биіктігі пирамиданың апофемасы деп аталады. Дұрыс пирамиданың:

бүйір қырлары тең;
бүйір жақтары тең;
апофемалары тең;
табанындағы екіжақты бұрыштары тең;
бүйір қырларындағы екіжақты бұрыштары тең.

Пирамиданың бүйір бетінің ауданы деп оның барлық бүйір жақтарының аудандарының қосындысын айтады. Пирамиданың бүйір бетінің ауданы оның табанының периметрінің жартысын пирамиданың апофемасына көбейткенге тең. Толық бетінің ауданы оның барлық жақтарының аудандарының қосындысына тең.

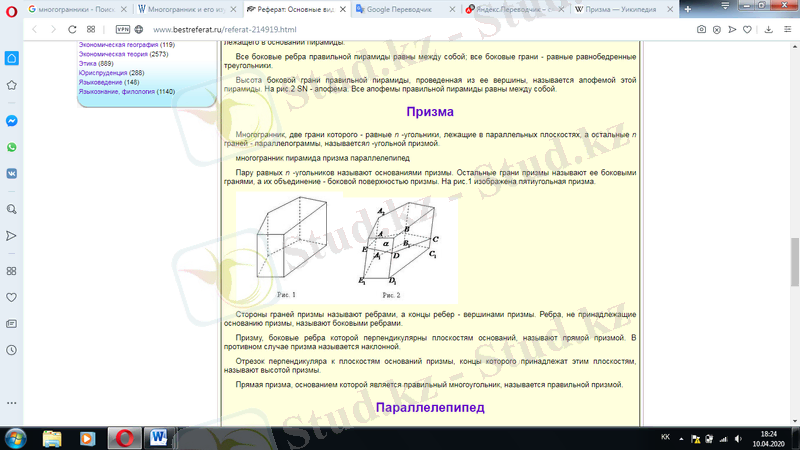Призма - табандары параллель жазықтықтарда жататын тең көпбұрыштардан тұратын, бүйір қырлары табандарына перпендикуляр кеңістік дене. Яғни әр түрлі жазықтықтарда жататын және параллель көшіргенде бір-біріне дәл келіп беттесетін екі көпбұрыштан және осы көпбұрыштардың сәйкес нүктелерін қосатын барлық кесінділерден тұратын көпжақты айтады. Көпбұрыштар-призманың табандары, ал сәйкес төбелерді қосатын кесінділер призманың бүйір қырлары деп аталады. Призманың табандары параллель жазықтықтарда жатады және тең болады; призманың бүйір қырлары параллель және тең болады. Призманың беті табандары мен бүйір бетінен құралады.

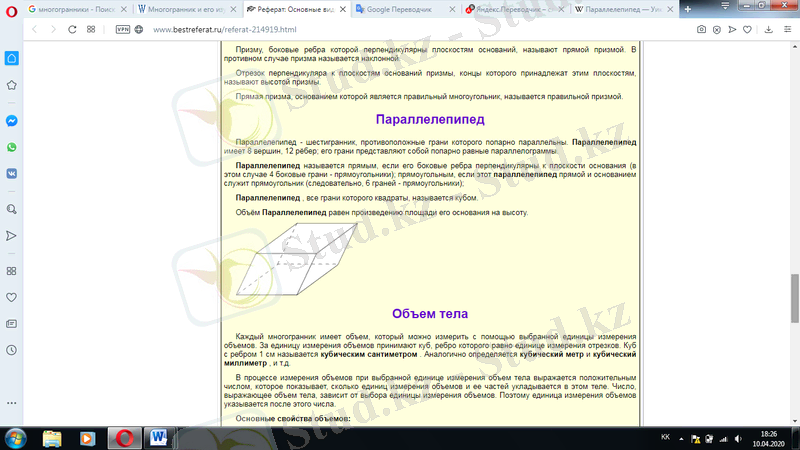Параллелепипед(грек. parallelos - параллель және epіpedon - жазықтық) - қарама-қарсы жақтары қос-қостан өзара параллель болатын алтыжақ. Параллелепипедтің 8 төбесі, 12 қабырғасы болады, оның жақтары қос-қостан бір-біріне тең параллелограмдар. Егер параллелепипедтің бүйір қабырғалары оның табан жазықтығына перпендикуляр болса (бұл жағдайда оның 4 бүйір жақтары - тік төртбұрыштар), онда ол тік параллелепипед деп аталады. Егер параллелепипед тік және табаны тік төртбұрыш болса (6 бүйір жақтары - тік төртбұрыш), онда ол тік бұрышты параллелепипед делінеді. Барлық жақтары квадрат параллелепипед “куб” деп аталады. Параллелепипедтің көлемі оның табан ауданы мен биіктігінің көбейтіндісіне тең болады.

Дұрыс көпжақтардың тарихы. Ежелгі грек философы Платон (428 немесе 427 б. з. д. - 348 немесе 347), Академаның тоғысында өз оқушыларымен әңгіме жүргізген (Академ - ежелгі грек мифологиялық кейіпкері, оның аңыз бойынша Афинаға жақын жерде қасиетті тоғайда жерленген, сол жерден аты шыққан, академия"), өз мектебінің ұрандарының бірі деп жариялады:, геометрияны білмейтін Платон жіберілмейді!”

Түйе-төрт түліктің төресі деп атайды, сондай-ақ Платоновыми тұрғыдан зерттеледі. Олардың белгілері Пифагорейцы Платонға бірнеше ғасыр бұрын. Диалогта, Тимей" ол төрт негізгі өлеңмен дұрыс көп қырлы байланыстырды. Тетраэдр отты бейнелейді, өйткені оның шыңы жоғары бағытталған; икосаэдр-су, өйткені ол ең "ағатын"; текше-ең "тұрақты" ретінде жер; октаэдр-ең "әуе" ретінде ауа. Бесінші сан қырлы, додекаэдр, "барлық тіршілік" өзіне жүзеге асырды, барлық әлемді бейнелейді, басты деп саналды. Дұрыс көп қырлы пифагорецтерге Платонға дейін бірнеше ғасыр бұрын белгілі болса да, оларды Платон денелері деп атайды. И. Кеплер әлемнің үйлесімді құрылымы жүйесіндегі дұрыс көп қырлы адамдар маңызды орын алды. Егер көп қырлы формаларды байқасаңыз және қарайтын болсақ, онда олардың сұлулығын сезініп қана қоймай, қолданбалы маңызы бар кейбір заңдылықтарды да анықтауға болады. Дұрыс және жартылай басқарылатын денелердің кейбірі табиғатта кристалдар түрінде, басқалары - вирустар, қарапайым микроорганизмдер түрінде кездеседі. Кристалдар-көп қырлы пішінді денелер. Бұл денелердің бір мысалы: Кристалл пирит (күкіртті колчедан FeS) - додекаэдраның табиғи моделі. Пирит (грек. "пир" - от) - күкіртті темір немесе күкіртті колчедан, сульфидтер тобынан ең көп таралған минерал. Пирит кристалдарының өлшемдері жиі бірнеше сантиметрге жетеді және жақсы коллекциялық материал. Оған ұқсас басқа минералдар қаттылығымен ерекшеленеді: шыны сызылады. Біздің Ана Жер дұрыс көлемді фигуралардың эволюциясын дәйекті түрде өтеді. Жердің құрылымы мен процестерін жоғарыда көрсетілген фигуралармен салыстыру туралы көптеген деректер бар. Жердің төрт геологиялық дәуіріне дұрыс платондық денелердің төрт күш қаңқасы сәйкес келеді: Протозою - тетраэдр (төрт плита) Палеозою - гексаэдр (алты плита) Мезозою - октаэдр (сегіз плита) Кайнозою - додекаэдр (он екі плита) .

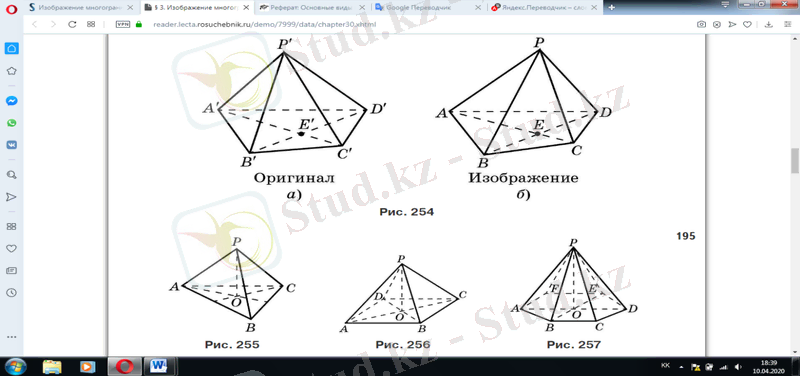Көпжақтарды кескіндеу. Көпжақты пішінінің толық бейнесін алу үшін, әдетте үш өзара перпендикуляр проекция жазықтығына проекция жасалады, жекелеген жағдайларда (салыстырмалы түрде қарапайым заттар үшін) екі проекция (әдетте фронталь және көлденең) жеткілікті. Мысал ретінде пирамиданы кескіндеуді қарастырайық:

P' A ' B ' C ' D ' төртбұрышты пирамидасының бейнесін құру үшін (сурет. 254, а) онда P' A ' B ' C үшбұрышты пирамида бөліп аламыз және оны pabc еркін толық төртбұрыш түрінде бейнелейміз (сурет. 254, б) . Осы пирамиданың d төбесінің d - бейнесі нүктесін салу қалды. Осы мақсатта осы пирамиданың негізі A' C' және B ' D ' диагоналін өткіземіз. E' = A' C'B' D ' Құралы Болсын. Параллельді жобалау кезінде бір түзуде жатқан үш нүктенің қарапайым қатынасы сақталатындықтан, онда A' E': E' C' = AE : EC ac кесіндісінде e нүктесін, ал B 'E': E ' d ' = BE : ED be сәулесінде d нүктесін саламыз. D нүктесін a, P және C нүктелерімен түзулермен біріктіріп, P ' A ' B ' C ' D ' төрт бұрышты пирамидасының pabcd ізделетін суретін аламыз. Бейненің көрнекілігіне жету үшін пирамиданың көрінетін қабырғаларын тұтас бөліктермен, ал көрінбейтін қабырғаларын штрихпен бөлеміз. Кез келген n-бұрышты пирамидасының бейнесі құрылады.

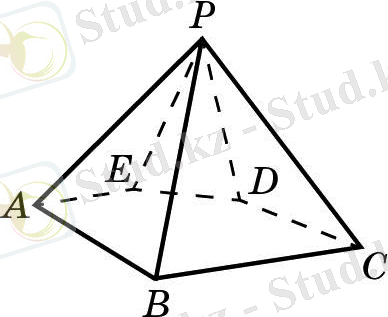Дұрыс пирамиданың дұрыс және көрнекі бейнесін құру үшін алдымен осы пирамиданың негізі мен оның ортасының бейнесін (көлденең орналасқан жазықтықта жақсы) салады. Содан кейін осы орталықтан тігінен жоғары қарай еркін нүктені көрсететін сәуле жүргізеді және оны осы пирамиданың ізделген бейнесі ретінде қабылдайды, ал осы төбені негіздің ортасын бейнелейтін нүктемен қосатын кесінді - осы дұрыс пирамиданың-түпнұсқаның биіктігінің бейнесі ретінде қабылдайды. 255, 256, 257-суретте PABC, PABCD, PABCDEF, ал 258-суретте pabcde еркін бесбұрышты пирамида бейнеленген.

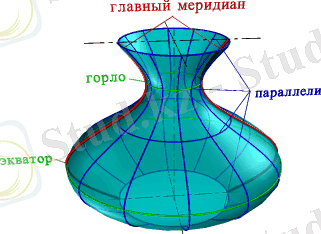Поверхности вращения Айналу беттері туралы түсінік. Айналудың беті-еркін сызықтың (түзу, жазық немесе кеңістіктік қисық) айнала айналғанда түзілетін бет. Мысалы, егер тік айналу осін қиып өтсе, онда оның айналуында конустық бет шығады, егер оське параллель болса - цилиндрлік, егер осьпен айқасқан болса - гиперболоид. Бір беті әртүрлі қисықтардың айналуымен алынуы мүмкін. Математикалық талдаудағы, аналитикалық және сызба геометриясындағы зерттеу объектісі болып табылады.

Айналу беттеріне мысалдар:

Айналмалы цилиндр беті (оған параллель түзу айнала алады) .
Конус (біріншісін қиып өтетін басқа түзудің айналасында түзудің айналуымен алынады) .
Сфера (сол жазықтықта жатқан және оның ортасынан өтетін осьтің айналасындағы шеңбердің айналуымен шығады) .
Тор (сол жазықтықта жатқан осьті қиып өтпейтін шеңбердің айналуымен шығады) .
Айналу Эллипсоид-екі жартылай осьтің ұзындығы сәйкес келетін эллипсоид(оның осьтерінің бірінің айналасында эллипстің айналуымен алынады) .
Параболоид айналу-өз осінің айналасындағы параболаның айналуымен алынған эллиптикалық параболоид.
Катеноид (тізбекті желінің айналуымен алынады) .

Қисық жазықтығында жатқан, бірақ қисық қиылыспайтын, осьтің айналасындағы соңғы ұзындықтағы жазық қисықтың айналуымен түзілген айналу бетінің ауданы қисық массасының ортасына дейінгі осьтен арақашықтыққа тең радиусы бар шеңбердің ұзындығына қисық ұзындығының туындысына тең. Бұл мәлімдеме Папп - Гульдиннің екінші теоремасы немесе Орталық туралы Папп теоремасы деп аталады. Қисық жазықтықта жатқан, бірақ қисық қиылыспайтын жазық тұйық өздігінен қиылысатын қисық айналумен түзілген айналу бетімен шектелген көлем қисықпен шектелген жазық фигура ауданының туындысына тең, осьтен жазық фигура ауырлығының ортасына дейінгі қашықтыққа тең радиусы бар шеңбердің ұзындығына тең.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.