Перпендикулярлы түзулерді құру

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 12 бет
Таңдаулыға:

Реферат

«Геометриялық тұрғызулар. Кесінділерді, бұрыштарды және шеңберлерді тең бөліктерге бөлу. Түйіндесулер. Коробтық және лекальдық қисықтар»

Орындаған:

Тобы:

Қабылдаған:

Жоспар:

Кіріспе
Перпендикулярлы және параллель түзулерді құру
Тік кесіндіні тең бөліктерге бөлу
Бұрыштарды өлшеу және тең бөліктерге бөлу
Шеңберлерді тең бөліктерге бөлу
Түйіндесулер
Коробтық қисықтар
Лекальдық қисықтар
Пайдаланылған әдебиеттер

Кіріспе

Геометриялық тұрғызулар деп геометрияның негізгі ережелеріне негізделген жазықтықтағы элементарлық құрылымдар түсініледі. Оларға мыналар жатады: өзара перпендикулярлы және параллель түзулерді жүргізу, кесінділерді, бұрыштарды бөлу және т. б. геометриялық құрылым циркульмен және сызғышпен (рейсшинмен) немесе сызғышпен және бұрыштармен орындалады. Геометриялық құрылымдарды білу кез келген бұйымның контурын дұрыс жазуға, сызба форматының рамкасын дәл орындауға және сызбаны оның ішінде дұрыс орналастыруға, жазуларды дәл белгілеуге мүмкіндік береді. Осылайша, геометриялық құрылыстар сызбаны орындау үшін негіз болып табылады. Оларды білу сызбаның орындалуын тездетеді, өйткені әрбір жағдайда құрудың ең тиімді тәсілдерін таңдауға мүмкіндік береді. Сонымен қатар, геометриялық құрылымдарды орындау сызба құралдарымен жұмыстың дұрыс тәсілдерін меңгеруге мүмкіндік береді. Графикалық құрылыс әрдайым дәл емес, бірақ дәлдік дәрежесі әртүрлі болуы мүмкін. Егер ол аз операциялар болса, құру дәлірек, (операция деп тура сызық жүргізуді, доғаны сызуды, кесіндіні кейінге қалдыруды және т. б. түсінеді) . Сондықтан құру тапсырмасын шешу кезінде ең қысқа жолды таңдау өте маңызды.

Геометриялық тұрғызулардың дәлдігі көбінесе жұмыс істеушінің ұқыптылығы мен назарынан тәуелді. Бұл ретте мыналарды ескеру қажет:

Жүргізілетін сызықтар жұқа болуы керек және оларды қатты қарындашпен сызу керек.
Сызбадағы нүктені екі сызықтың қиылысу нүктесі ретінде қою керек: екі түзу, екі доға немесе түзу және доға. Барлық жағдайларда осы сызықтардың арасындағы бұрыш түзу немесе оған жақындауға ұмтылу керек.
Екі нүкте арқылы тікелей өткізе отырып, оларды бір-бірінен алыс алған жөн, себебі нүктелерді жақындастыру кезінде тура оның шынайы бағытынан ауытқу мүмкіндігі артады.

Перпендикулярлы және параллель түзулерді құру

Перпендикулярлы түзулерді құру. Берілген A нүктесінде перпендикулярды mn түзуге тұрғызу (1, а-сурет) . A нүктесін центрден және R1 еркін радиусымен қабылдайды доғаны оның O1 және O2 нүктелерінде R2 радиусы үлкен R1 радиусымен қиылысқанға дейін сипаттайды, O1 және O2 орталықтарынан доғаларды B және С нүктелерінде өзара қиылысқанға дейін жүргізеді, B және C түзу нүктелерін қосып, ізделінетін перпендикуляр алады.

1, б-суретте сол тапсырма сызғыш пен бұрыштаманың көмегімен шешілді. Тік MN көмірді катетпен (көмірдің жағдайы I), ал оның гипотенузасына сызғышты немесе басқа бұрыштарды қосады. Сол қолмен сызғышты ұстай отырып, бұрыштаманы оның екінші аяғы А нүктесімен сәйкес келгенге дейін оң жаққа жылжытады (бұрыштаманың жағдайы II), содан кейін берілген сызғышқа перпендикуляр тура жүргізеді.

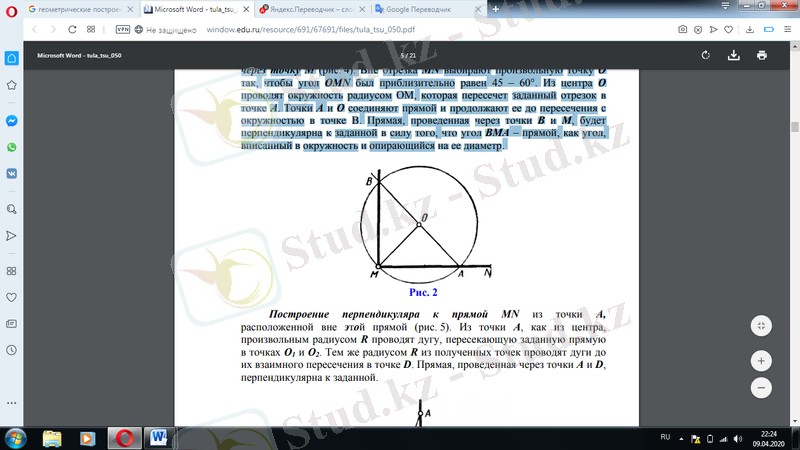
MN кесіндісіне перпендикуляр және М нүктесі арқылы өтетін түзу құру (2-сурет) . MN бөлігінен тыс OMN бұрышы шамамен 45 - 60°тең болатындай етіп еркін нүктені таңдайды. В және M нүктелері арқылы жүргізілген түзу ВМА бұрышы шеңберге жазылған және оның диаметріне тірелетін бұрыш сияқты тік бұрышқа берілген бұрышқа перпендикуляр болады.

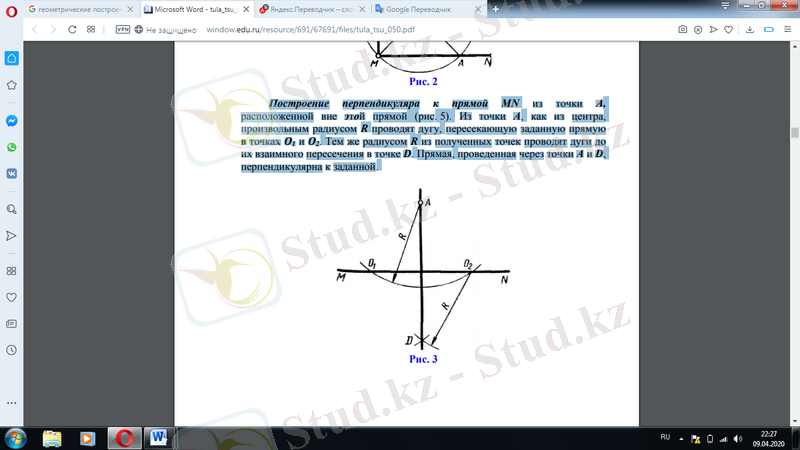Осы түзуден тыс орналасқан А нүктесінен тік MN-ге перпендикуляр құру (3-сурет) . А нүктесінен, ортасынан, R еркін радиусы O1 және O2 нүктелерінде берілген түзу қиып өтетін доғаны жүргізеді. Алынған нүктелерден сол R радиусы доғалар D нүктесінде өзара қиылысқанға дейін жүргізеді.

Параллель түзулерді құру. Осы сызықтан тыс орналасқан А нүктесі арқылы берілген MN сызығына параллель сызық сызыңыз (4, а-сурет) . А нүктесінен М радиусын В және С нүктелерімен қиылысатын шеңбер сызылады, олардың біреуінен, мысалы, С нүктесінен, MN түзуінде R радиусына тең кесінді кез-келген бағытта салынып, D нүктесінен алынады, D нүктесінен бірдей болады. радиусымен доғаны ол Е нүктесінде шеңбермен қиылысқанша сызады, AE және CD сегменттері ACDE ромбының қарама-қарсы жақтары болғандықтан, AE түзу сызығы MN-ге параллель болып табылады.

Тік кесіндіні тең бөліктерге бөлу

АВ кесіндісін жартыға бөлу (1, а-сурет) . R радиусы AB кесіндісінің ұшынан M және N нүктелерімен қиылысқанша екі доғалар тартылады, олар M және N нүктелерімен қиылысқанша, осы сегментті С нүктесінде жартысына бөледі.

Егер біз кесіндіні бөліп, оның жартысын біртіндеп екі есе азайтуды жалғастырсақ, онда АВ кесіндісі тең бөліктерге 4, 8, 16 және т. б. бөлінеді (1, б-сурет) .

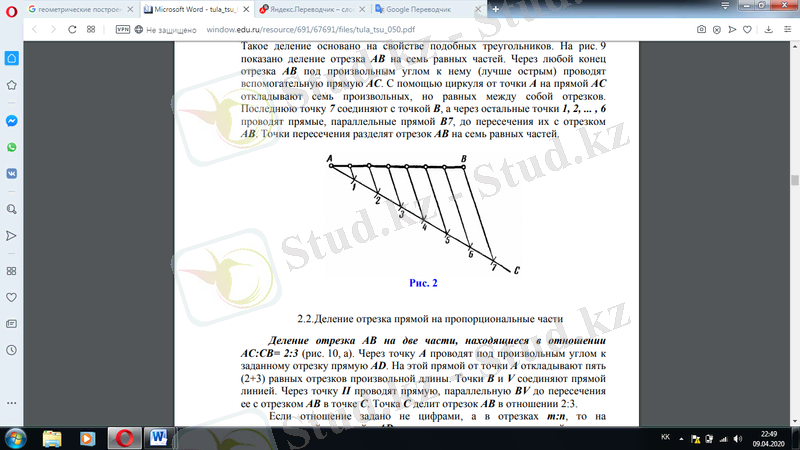Сызықтық сегментті тең бөліктердің кез-келген санына бөлу. Бұл бөлу осындай үшбұрыштардың қасиетіне негізделген. 2-суретте АВ кесіндісін жеті тең бөлікке бөлуді көрсетеді. Көмекші айнымалы сызық AB кесіндісінің кез-келген нүктесінен оған еркін бұрышпен тартылады (жақсырақ өткір) . А нүктесінен компасты қолдана отырып, жеті еркін, бірақ бір-біріне тең, сегменттер АС сызығына қойылады. Соңғы 7 нүкте В нүктесіне қосылады, ал қалған 1, 2, . . . , 6 нүктелері арқылы AB7 кесіндісімен қиылысқанша В7 сызығына параллель түзу сызықтар салынады. Қиылысу нүктелері AB сегментін жеті тең бөлікке бөледі.

Бұрыштарды өлшеу және тең бөліктерге бөлу

Бұрыштарды өлшеу. 4-суретте протектордың ABC бұрышын өлшеуін көрсетеді. Протектордың бастапқы түзу сызығы өлшенген бұрыштың бір жағымен біріктіріледі, осылайша В шыңы О нүктесіне сәйкес келеді, содан кейін бұрыштың екінші жағымен сәйкес келетін масштабтың бөлінуі өлшенген бұрыштың градус санын көрсетеді.

Бұрышты тең жарты бөлікке бөлу. Кездейсоқ радиусы R1 болатын ABC В шыңынан доғаны ол М және Н нүктелеріндегі бұрыштармен қиылысқанша сызыңыз, содан кейін M және N нүктелерінен радиус> R1 доғаларын D нүктесіне қиылысқанша сызыңыз, BD түзу сызығы бұл бұрышты жартысына бөледі. Бұрышты 4, 8 және т. б. тең бөліктерге бөлу бұрыштың әр бөлігінің жартысында кезекпен бөліну арқылы жүзеге асырылады (5, б-сурет) .

Бұрышты сызбада қиылыспайтын тараптар орнатқан жағдайда, мысалы, 5, в-суреттегі АВ және CD, бұрышты жартыға бөлу келесідей орындалады. Кездейсоқ, бірақ бұрыштың екі жағынан бірдей қашықтықта KL сызықтарын сызыңыз AB және MN CD-ге салыңыз және оларды О нүктесінде қиылысқанша жалғастырыңыз. Соның нәтижесінде алынған бұрышы OF түзу сызығымен жартысына бөлінеді. OF сызығы берілген бұрышты екі есе азайтады.

Дұрыс бұрышты үш тең бөлікке бөлу (17-сурет) . Дұрыс бұрыштың шыңынан - В нүктесі, радиустың кез келген екі жағымен А және С нүктелерімен қиылысқанша, R радиусының доғасын сызыңыз, А және С нүктелерінен бірдей радиусы бар R доғаларын сызыңыз, M және N нүктелерінде айнымалы ток доғасымен қиылысқа салыңыз. В бұрышы мен M және N нүктелерінің шыңдары арқылы дұрыс бұрышты үш тең бөлікке бөліңіз.

Шеңберлерді тең бөліктерге бөлу

Шеңберді жартыға бөлу үшін кез-келген диаметрді жүргізу жеткілікті. Екі өзара перпендикуляр диаметр шеңберді төрт тең бөлікке бөледі (1, а-сурет) . Әр төртінші бөлікті жартысына бөліп, сіз сегізінші бөлікті аласыз, ал одан кейінгі бөліністер он алтыдан, отыз екінші бөліктен және т. с. с. болады (1, б-сурет) . Егер бөлу нүктелерін түзу сызықтармен жалғасаңыз, онда сіз тұрақты жазылатын квадраттың (а4), сегізбұрыштың (а8) және т. б. бүйірлерін алуға болады (1, с-сурет) .

Шеңберді 3, 6, 12 және т, д. тең бөліктерге бөлу, сондай-ақ тиісті дұрыс жазылған көпбұрыштарды тұрғызу былайша жүзеге асырылады. Шеңберде екі өзара перпендикуляр диаметр 1-2 және 3-4 жүргізеді (2, а-сурет) . Орталықтардан 1 және 2 нүктелерден доғаларды R шеңбердің радиусымен оған А, В, С және D нүктелерінде қиылысқанға дейін сипаттайды. Сол нүктелер шеңберді тең үш бөлікке бөледі (2, б-сурет) . Шеңберді 12 тең бөлікке бөлу үшін 3 және 4 нүктелерінен шеңбер радиусымен тағы екі 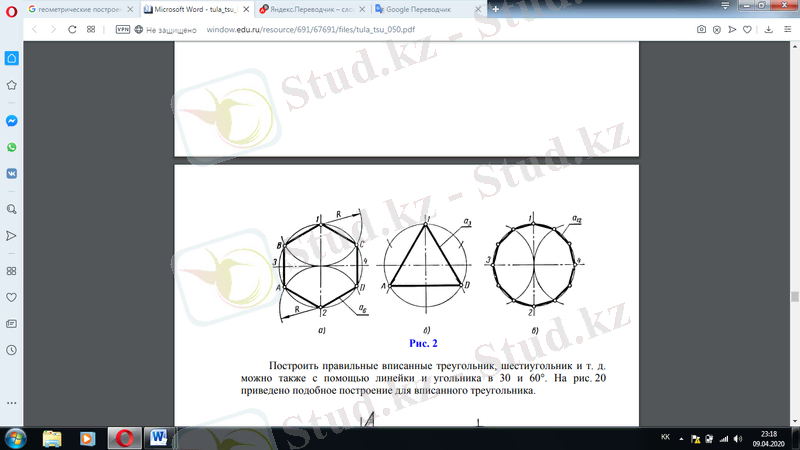доғаны сипаттайды (2, в-сурет) .

Шеңберді бес немесе он тең бөліктерге бөлу үшін екі өзара перпендикуляр диаметр жүргізіледі (5, а-сурет) . OA радиусы екіге бөлінеді және В нүктесін алып, одан R = BC радиусымен доғаны көлденең диаметрі бар D нүктесінде қиылысқанға дейін сипаттайды. C және D нүктелерінің арасындағы қашықтық дұрыс жазылған бесбұрыштың (а5) жағының ұзындығына тең, ал OD кесіндісі дұрыс жазылған онбұрыштың (А10) жағының ұзындығына тең. Шеңберді бес және он тең бөлікке бөлу, сондай-ақ жазылған дұрыс бесбұрыш пен он бұрышты тұрғызу 5, б-суретте көрсетілген. Шеңберді бес бөлікке бөлудің мысалы бес бұрышты жұлдыз болып табылады (5, в-сурет) .

6-суретте шеңберді тең бөліктерге жақындатудың жалпы тәсілі келтірілген. Шеңберді тоғыз тең бөлікке бөлу қажет болсын. Шеңберде екі өзара перпендикулярлы диаметр жүргізеді және Ab тік диаметрі қосалқы түзудің көмегімен тоғыз тең бөлікке бөлінеді (6, а-сурет) . B нүктесінен R = AB радиусымен доғаны сипаттайды және оның көлденең диаметрімен қиылысқан жерінде С және D нүктелерін алады. Сәулелердің шеңбермен қиылысу нүктелері оны тоғыз тең бөлікке бөледі (6, б-сурет) .

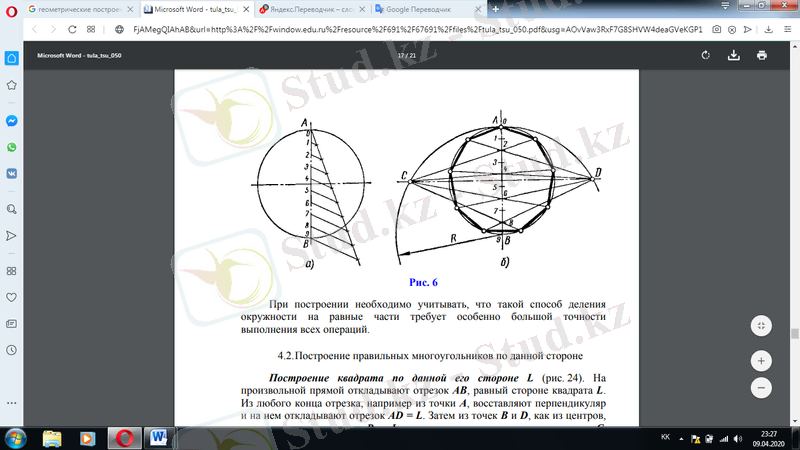
Құрастырулар кезінде шеңберді тең бөліктерге бөлудің осындай тәсілі барлық операцияларды орындаудың ерекше үлкен дәлдігін талап ететінін ескеру қажет.

Түйіндесулер

Түйіндесулер деп бір сызықтың екінші сызыққа бір қалыпты өтуі деп аталады. Түйіндестірулерді құру үшін жұптастыру орталығы мен жұптастыру нүктесін табу керек. Түйісу нүктесі-түйісу сызықтары үшін ортақ нүкте. Түйісу нүктесі де өту нүктесі деп аталады. Төменде негізгі жұптастыру түрлері қарастырылады.

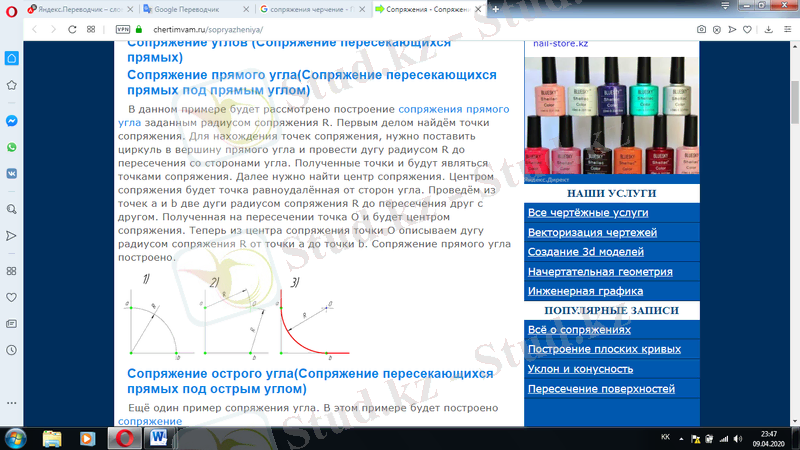R түйіндесу радиусымен тікелей бұрыштың түйісуін құру мысалын қарастырылады. Табу үшін нүктесі жанасу, қою керек циркуль в шыңына бұрышының тікелей және өткізу доғасы мен радиусы R қиылысына дейін тараптармен бұрышының. Алынған нүктелер түйісу нүктелері болады. Содан кейін жұптастыру орталығын табу керек. Жанасу орталығы жағынан тең нүкте болады. A және b нүктелерінен бір-бірімен қиылысқанға дейін екі доғаны R түйіндеу радиусымен өткіземіз. Қиылыста алынған нүкте О және түйісу орталығы болады. Енді нүктенің түйісу ортасынан доғаны R түйісу радиусымен а нүктесінен b нүктесіне дейін сипаттаймыз. Тік бұрыш үшін түйіндесу құрылды.

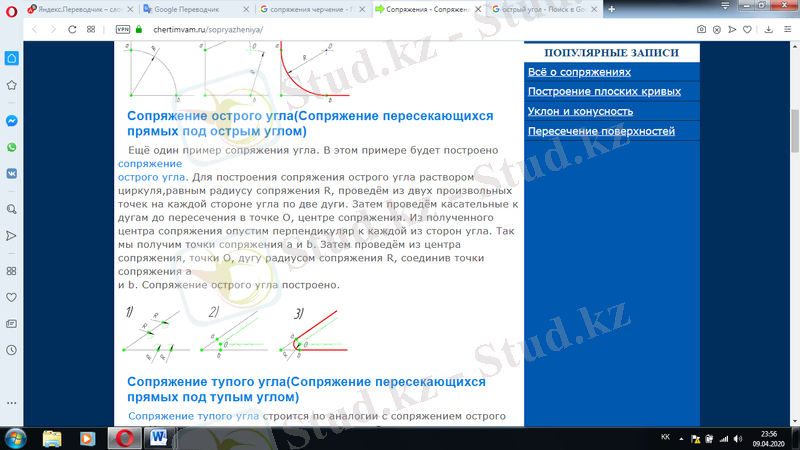Бұрышты түйіндестірудің тағы бір мысалы. Бұл мысалда өткір бұрышты түйіндесу жасалады. Түйіндесу радиусына R тең болатын циркульдің ерітіндісімен жедел бұрыштық түйіндесуді құру үшін бұрыштың екі жағындағы екі еркін нүктеден екі доғаны сызамыз. Содан кейін тангенстерді доғаларға түйісу орталығы О нүктесінде қиылысқанша тартамыз. Алынған түйісу центрінен бұрыштың екі жағына перпендикуляр түсіреміз. Сонымен а және b түйіндесу нүктелерін аламыз. Содан кейін біз түйіндесу центрінен, O нүктесін, а және b конъюгация нүктелерін байланыстыратын радиусы R доғаны аламыз. Сонымен өткір бұрышты түйіндесу пайда болды.

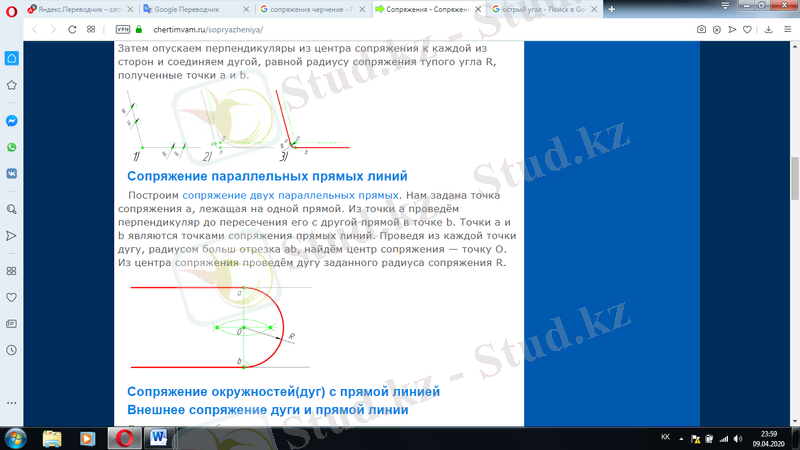Параллель түзу сызықтардың түйіндестіру. Екі параллель түзудің түйіндесуін құрайық. Бізге бір түзуге жататын a түйіндеу нүктесі берілген. A нүктесінен перпендикулярды b нүктесіндегі басқа түзумен қиылысқанға дейін жүргіземіз. Әрбір нүктеден доғаны, радиус арқылы AB үлкен бөлігін жүргізіп, түйіндеу орталығын - o нүктесін табамыз.

Аралас доғалардың түйіндесуінің бірінің орталығы (O1) олардың R радиусының жанасатын доғаларының шегінен тыс, ал басқа шеңбердің ортасы(O2) - оның ішінде жатқан доғалардың түйісуі болып табылады. R1 нүктесінің радиусының ортасынан O1, және R-R2 нүктесінің радиусының ортасынан O2 нүктесінің радиусының ортасынан R+R1 радиусының доғасын табамыз. Осыдан кейін o нүктесін O1 және O2 шеңберінің ортасымен тура байланыстырамыз және тиісті шеңбердің сызықтарымен қиылысқанда A және B түйіндесу нүктелерін аламыз.

Коробтық қисықтар

Машиналардың кейбір бөлшектерінің, металдарды өңдеуге арналған құралдардың әртүрлі диаметрлі шеңберлердің өзара созылатын доғаларынан тұратын тұйық қисық сызықтармен шектелген контурлары болады. Коробтық қисықтар деп шеңбер доғаларының түйіндесулерінің нәтижесінде пайда болатын қисықтар аталады. Мұндай қисықтарға овалдар, овидтер, бұйралар жатады.

Овоид құру. Овоид - симметрияның тек бір осі бар жабық коробты қисық. Орталық овоид симметриясының осінде жатқан шеңбердің R және R1 радиустары бір-біріне тең емес. Берілген АВ осі бойынша овоид құру келесі ретпен орындалады: АВ овоид осіне тең диаметрі бар шеңберді жүргізеді. А және В нүктелерінен О1 нүктесі арқылы (R радиусы шеңберінің симметрия осімен қиылысу нүктесі) түзу жүргізеді. А және В нүктелерінен, Р2 радиусы, АВ осіне тең, an және Bm доғаларын жүргізеді, ал О1 орталығынан R1 радиусы NM овоидінің кіші доғасын жүргізеді.

Овалды құру. Овал - симметриялық екі осі бар жабық коробты қисық. Берілген өлшем бойынша овалды құру реті овал АВ осінің үлкен осі мынадай түрде жүргізіледі. АВ осі тең үш бөлікке бөлінеді (АО1, О1О2, О2В) . N және M нүктелерін О1 және О2 нүктелерімен жалғай отырып, шеңберлермен қиылысқанға дейін жалғастыратын түзу пО1, пО2, мО1, мО2 алады. Алынған нүктелер 1, 2, 3, және 4 доғалардың түйіндеу нүктелері болып табылады. M және n нүктелерінен, N2 және m3 тең R1 радиусы орталықтардан, 12 жоғарғы доғаны және 34 төменгі доғаны жүргізеді.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.