Экожүйелерді математикалық модельдеудің теориялық негіздерін оқыту әдістемесі


МАЗМҰНЫ
ЭКОЖҮЙЕЛЕРДІ МАТЕМАТИКАЛЫҚ МОДЕЛЬДЕУ ҚҰРЫЛЫМНЫҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІН ОҚЫТУ ӘДІСТЕМЕСІ
НАРМАТИВТІК СІЛТЕМЕЛЕР . . . 3
АНЫҚТАМАЛАР . . . 4
ҚЫСҚАРТУЛАР ТІЗІМІ . . . 5
КІРІСПЕ
Жалпы математикалық модельдеу ұғымын қысқаша сипаттайтын болсақ: ол кез келген құбылыстарды, күрделі физикалық үрдістерді және аппараттарды зерттеу арқылы олардың математикалық модельдерін құру. Ал соның ішінде математикалық модель дегеніміз - математикалық қатынастар түрінде жазылған, техникалық объект немесе құбылыс туралы білімдердің, ұсыныстардың және ғылыми болжам жиынтығы. Математикалық моделдеуге кез келген математикалық мүмкіндіктерді пайдалануға болады. Мысалы, дифференциалдық немесе интегралдық теңдеулерді, жиындар теориясын, абстрактылық алгебраны, математикалық логиканы, ықтималдықтар теориясын және тағы сол сияқты. Модель жүйенің бейнесін анықтауға, сол туралы түсінікті жетілдіруге жиі қолданылатын құрал. Ал енді соның ішінде экология саласындағы моделдеу туралы айтуды заман талап етіп отырған тәрізді. Сағат санап өзгеріп жатқан тынымсыз дүниеде, қоршаған ортаның әр түрлі заттармен ластанып жатқаны баршамызға аян. Экология пәні көптеген ғылыми пәндердің жиынтығы, атап айтсақ: биология, физика, геология, химия, география, экономика, әлеуметтану, математикалық модельдеу, құқықтану т. с. с. Дегенмен экологияның даму кезеңдерін еске түсіретін болсақ, онда оның ағзалардың қоршаған ортамен әрекетін зерттейтін ботаника және зоология деп аталатын екі бөліктері екендігін білеміз. XX ғасырдың ортасына таман экология ғылымының зерттеу аумағы ұлғайып, ағзаларды қоршаған ортамен байланыстыра зерттейтін, «жалпы экология» деп аталатын биологияның үлкен бір саласына айналып отыр. Бүгінгі таңда экология тек пәнаралық байланыс ретінде ғана қалып қоймай, жалпы ғылыми маңызыдылығы жоғары ерекше дара пәнге айналды. Жалпы экология пәні - қоршаған ортадағы болмысты толық баяндайтын ғылыми негізі қалыптасқан әдістемелік ғылым ретінде шаруашылықтың әр саласында нәтижелі қолданыс тауып отыр. Енді осындай экожүйелерді ғылыми түрде байланыстыра отырып, ондағы есептеулердің нәтижелерін математикалық моделдеу арқылы көрсете білудің маңызы өте зор. Зерттелетін экологиялық үдерістерге сандық баға беруге математикалық модельдеу мүмкіндік жасайды. Қандайда бір жинақталған мәліметтерді пайдаланып, қоршаған ортадағы экологиялық процестер мен жағдайлардың даму мүмкіндіктерін математикалық моделдеу арқылы болжауға болады.
Қоршаған ортадағы обьектілер мен процестерді математикалық моделдеудің ерекшеліктері және оның экология жүйесіндегі алатын орны қарастырылған. Соның ішінде экология саласындағы математикалық моделдеудің заманауи бағыттағы маңыздылығы және экологиялық жүйелерді қорғап, дамыту үшін математикалық модельдеудің рөлі талқыланады. Математиканың экологиямен байланысын тереңдеп оқыту - экологиялық процестер мен жағдайлардың даму мүмкіндіктерін математикалық моделдеу арқылы болжауға болады. Экологиялық процестерді зерттеу үшін математикалық модельдерді алудың кейбір жолдарын түсіну қажет. Сондықтан табиғаттағы құбылыстарды зерттеуде қолданылатын математикалық модельдердің негізгі принциптерін білген жөн.
Экожүйелер - бір-бірімен және қоршаған жансыз бөлігімен байланысқа түсетін тірі ағзалардың өз-өздерін қолдай алатын жүйелрі. Қоршаған ортаның сапасы және оның негізгі құрамдас бөліктерінің әлеуетті мүмкіндіктерін талдау және оның жай-күйін бақылау жүйесінің мониторингін нақты ұйымдастыруды болжайды. Бұл ретте қазіргі заманғы экологиялық дағдарыс жағдайында қоршаған ортаны жан-жақты талдаудың токсикологиялық аспектілері ерекше маңызға ие болады. Қазіргі уақытта ғылыми және өндірістік ортада шекті жол берілетін шоғырлану жүйесіне негізделген табиғи объектілерге ластаушы заттардың төгінділері мен шығарындыларын нормалау тұжырымдамасының шектеулілігі бізге түсінікті. Экология-тірі организмдердің, соның ішінде адамның қоршаған ортамен өзара іс-қимылы туралы барлық ғылымдардың түсініктерін қамтитын, білім саласы. 20 ғасырдың ортасына дейін экология биологиялық пәндердің бірі болып табылады, атап айтқанда, организмдердің қоршаған ортамен өзара әрекеттесуі туралы ғылым. Қазіргі заманғы экология сонымен қатар ғылым мен қоршаған ортаның жай - күйін бақылаудың практикалық әдістері-мониторинг, қоршаған ортаны қорғау, биогеоценоз және табиғи экологиялық жүйелерге аторопологиялық әсер ету туралы ілім, экологиялық-экономикалық және экологиялық-әлеуметтік аспектілер кіреді. Осының бәрі экология мәселелерін шешуде қолданылатын математикалық модельдер мен әдістерді біріктіретін математикалық экология пәнін де анықтайды.
1. 1. Модель және математикалық модельдеу ұғымы Модель дегеніміз - нақты объектіні, процессті немесе құбылысты ықшам әрі шағын түрде бейнелеп көрсету. Модельдеу - объектілерді, процесстерді немесе құбылыстарды зерттеу мақсатында олардың моделін (макетін) құру. Модель - көрнекі түрде жазбаша жоспар, сызба ретінде жасалуы мүмкін. Мұндай модель барлық уақытта біздің ойымызда бейнеленетін прототип пайда болғанға дейін жасалады. Бір объект үшін әр түрлі модель жасалуы мүмкін. Модельдің жасалуы зерттеу мақсатына және прототип жөнінде жинақталған мәліметтердің көлеміне тәуелді болады. . Мысалы, жуық арада басқа қалаға қыдырып баратын болдық делік. Ол қала туралы өзіміз білетін мәліметтерді жинақтап, ойымызды қорытып, қиялымызда сол қаланың моделін жасай бастаймыз. Мұндағы мақсатымыз - басқа қаламен танысу. Қаланы аралап келгеннен соң, толық мәлімет алғандықтан, ойымыздағы модель өзгеруі мүмкін. Ал сол қаланың сеулетші жасаған моделі мүлде өзгеше болады. Қоршаған ортамен араласып, қарым - қатынас жасаудің нәтижесінде адам өз танымына қарай модель құрайды. Танымдық процесс зерттелінетін (танылатын) обьектіге және зерттеуші (танушы) субьектіге байланысты. Зерттелетін обьектіде болып жатқан оқиғаны бақылап, керек болса оқиғаға кірісіп, қойған сұрақтарына жауап алумен қатар, обьектіге қатысты информацияларды жинақтап, қорытып, субьект пен обьектіге тән құбылысты түсініп, өзінің көзқарасын белгілі бір формада бекітеді. Осы затқа тән нақтылы информацияларға негізделген зерттеушінің обьективтік танымы - обьектінің моделі болып есептелінеді.
Қазіргі жаһанданған заманда ғылыми технологияның дамуы, экономиканың өркендеуіне байланысты экожүйелерін математикалық модельдеудің маңыздылығы да күн санап артып келеді. Экологиялық проблемаларды шешу кешенді және сандық тәсілді талап етеді, сол себепті сандық талдау және пәнаралық синтез мүмкіндіктерімен математикалық үлгілеу әдісі, бақылау және экспримент әдістерін толықтыру арқылы неғұрлым өзектілікке ие бола аламыз.
Математикалық модельдеу : өмірде болып жатқан құбылыстарды немесе күрделі физикалық процестерді, аппараттарды олардың математикалық модельдерін құру арқылы зерттеу тәсілі яғни, математикалық модельді құру үрдісі болып табылады. Математикалық модель деп обьектінің қызметі мен құрлымын сипаттайтын математикалық тәуелділіктер жүйесі, математикалық формулалар мен теңдеулер арқылы өрнектелетін обьектілердің математикалық сипаттамалары болып табылады.
Сөйтіп танымдық процестің негізгі қызыметі - информацияны жинау, сақтау және қорыту болса, модельдеудің негізінде де осылар жатыр деуге болады.
Қоршаған дүниені жүйелі ұғудың танымдық типтерін, әрі нақтылы процесті сипаттаудың жолы әртүрлі. Бұған жататандар ғылым, философия, дін, мәдениет, әдебиет . . . Ал бұларға тән ортақ баланыс бар ма? Әр ғылым иесі өз тұжырымын жасайды. Мысалы, дін - адамның мәңгілік жасау мүмкіндігінің, құдайдың қағыйдалық ұғымдары туралы; жазушы детективтік роман немесе трагедиялық әңгіме жазады; суретші таң шапағындағы күннің шығу кезіндегі құбылысты беретін суреттер салса, ал композитор бір оқиғаға арнап симфония жазуы мүмкін . . .
Модельдің түрлері көп. Модельдеудің жалпы үлкен екі топқа бөлінеді: материалдық (заттық) және идеалдық. Материалдық дегеніміз - зерттелінетін обьектінің геометриялық, физикалық, динамикалық және функционалдық сипаттамасына негізделеді. Сондықтан материалдық таным физикалық және аналогтық болып бөлінеді.
Физикалық модельдеуге - ұқсастық теория негізінде нақты обьектінің кішірейтілген немесе үлкейтілген көшірмесін қолданып, лобораториялық жағдайда процесті қайталап, тәжірибе жасап ұғу жатады.
Аналогтік модельдеуге - зерттелнетін обьектілердің физикалық табиғаты әртүрлі құбылыстарда жүретін процесстердің арасындағы байланысты білдіретін ұқсастық теорияны қолданып, зерттеу жатады. Мұндай процестер бірде математикалық теңдеумен, немесе логикалық сызбалармен беріледі. Қарапайым мысал ретінде механикалық тербелістерді электірлік сұлба бойынша зерттеуге болады. Мұндағы процестер аналогиялық құбылыстарға жатады, сондықтан да екеуі де бірдей теңдеумен сипатталады.
Бұл екі тиіптес модельдер берілген обьектілердің заттық баламасына негізделген, өзара геометриялық, физикалық және басқа сипаттамалармен байланыста қарастырылады. Сондықтан материалдық модельдеу өзінің табиғаты жағынан эксперименттік тәсілге жатады.
Заттық моделдеуден идеалдық модельдеу принципі мүлде басқа. Заттық зерттеу обьекті мен модельдің материалдық аналогиясына негізделсе, идеалдық зерттеу танымдық процестің негізінде құрылған ойдың, идеалдық аналогиясының жемісі боп табылады.
Сөйтіп, идеалдық модельдеу теориялық сипаттамадан тұрады да, интуитивтік және таңбалық болып екіге бөлінеді. Интуитивтік модельдеу дегеніміз - зерттелетін обьекті мен зерттеушінің сезім мүшелеріне әсер етуіне байланысты топшыланған информациялардың жиынтығы. Мысалы, адамның өмірде жинаған тәжірибсі қоршаған дүниенің интуитивтік моделі болады т. б. ; Таңбалық модель - зерттелінетін обьектіге қатысты информацияны белгілі бір тәртіпке сүйеніп, таңбаларға түрлендіреміз. Мысалы, сүлбеге, графиікке, сызбаға, формулаға, т. б. таңбаларға жинақтау. Таңбалық модель құрылымын зерттейтін элементтер заңдылыққа, алгоритмге бағынып, өзіне тән ережелер жүесінде жұмыс істейді. Математикалық модель - таңбалық танымның негізіне жатады. Классикалық мысал ретінде механиканың заңдарын, И. Ньютонның математикалық формулаларын қолданып зрттеуге болады.
Экожүйе дүниесіндегі обьектілердің ғылыми танымдылығын жеткізу үшін әртүрлі математикалық тәсілдердің қолданыстарын пайымдайық. Ол үшін аздап математиканың маңызына және оның басқа ғылымдармен байланысына, әрі кейбір ерекшеліктеріне тоқталайық.
Өмірде кездесетін ғылымдардың көбі бір - бірімен тығыз байланыста болғанымен, қолдану шегарасы айқындалған. Физикамен айналысатын таза физик жекеменшік формаларының өзара қатынасын түсіндіре алмайды. Ал өзінің қадірін білетін математиктің алдында ешқандай кедергі тұрмайды. Әртүрлі ғылыми пәндердің жасанды шекарасы математика моделін қолдануға бөгет болмайды. Таза математик бола тұрып, адамзаттың әртүрлі формадағы қызыметіне батыл кірісіп, айтарлықтай жетістіктерге жетеді. Осыдан математика өзіне тән қасиеттер арқылы, барлық саланы қамытуға тырысқандығы және нақты не бере алады деген ой туады.
Математика мен бізді қоршаған нақты өмірді байланыструшы арнайы түйіннің түрі - модель болады. Сонымен, модель бір жағынан зерттелетін обьектіге тиісті бай информатцияны қамтыса, екінші жағынан математикалық стандартты формула таңбаларынан тұрады. Сөйтіп, математикалық аппаратты қолдануға мүмкіндік береді. Бұл дегеніміз - зерттелінетін құбылыстың Математикалық моделі. Ол нақты ғылыми заңдылықтардың негізінде математикалық тілге аударылып қызымет істейді, танымның дамуына жол ашады. Жалпы математикалық модель принципті түрде әртүрлі екі дүниені қосатын ұлы көпір. Біреуі - қоршаған обьективтік шындық. Ол біздің сана-сезімімізге әсер етеді. Екіншісі - жеке адамзаттың идеясына сүйенген, құдіретті математика заңына бағынған абстрактік дүние.
Біздің мақсатымыз - экожүйелері математикалық модельдеуді шынайы өмірде қолдануға болатын теориялық оқыту әдістемесін зерттеу, оқушылардың дүниетанымына қажетті математикалық көпір құруды үйрету болып табылады.
Енді ғылыми зерттеудегі мазмұн мен форманың байланысы, оның ішінде математикалық модельдеудің мәні қандай? Кез - келген модельдің мақсаты - қарастырылатын обьект туралы информацияны жеткізу болғандықтан, мазмұнын модельдеу, формаға қарағанда басым болады. Ал математикалық модель бейнелейтін нақтылы дүниеге адекватты болады, сондықтан формаға және мазмұнға қойылатын талап бірдей. Математикалық танымның алдындағы кейбір этаптарды қарастырайық. Зерттелетін құбылысқа қойылған моделмен зерттеуші қандай проблеманы шешпек, қандай математикалық аппаратты, тәсілді және техниканы қолданбақ, жетілген құрал - жабдықтарға, білімге байланысты нақтылы шындыққа барынша жақындап, нақты информация алуға болады десек артық болар. Әрине, бұдан математикалық аппараттың негізінде абсолютті дәл немесе ықтималдылығы басым эталондық модель аламыз деген ой тумайды.
Модельдеу дегеніміз - неізгі информацияны жинап, сақтап, түрлендіру болып табылады. Сондықтан бір обьектінің екі моделін салыстырсақ, қайсысының информацияны түрлендіру эффектілігі басым, сол модель жақсы делінеді. Кейде абстрактілі математикалық модельден қосымша енгізілген түзетулердің көмегімен информацияларды өңдеп зерттелетін процесс туралы нақты деректер алуға болады. Бірақ мұндай модельді, өмірде қолдану ойдағыдай болмайды.
Математикалық модельдер. Математикалық модельдермен зерттелетін объекті мен үрдістің қасиеттері, ерекшеліктері және сипаттамалары теңдеулер жүйелері, теңсіздіктер және функция арқылы көрсетіледі.
Көптеген математикалық модельдеруниверсалды болып келеді, . Математикалық модельдер қарастырылатын құбылыстар мен үрдістердің сандық заңдылықтарын анықтауға, сипатталатын факторлардың тәуелділігі мен .
Математикалық модельдердің дамуына өте күрделі есептеулерді жүргізетін электронды-есептегіш машиналарының көбеюі зор ықпал етті.
. Айнымалышамалар, мысалы, өндірілгенөнімкөлемі, капиталжұмсау, тасымалдаут. с. с., алпараметрлер , уақыт, . .
1) Сыртқыайнымалылар-;
2) Ішкіайнымалылар, модельді зерттеу қорытындысында анықталады.
Модельдеу үрдісінің нақты алгоритмі жоқ, бірақ модельдеу тәжірибесінде басшылықққа алатын анықталған принциптер бар.
Математикалық модельдердің құрылымдық және функционалдық түрлері бар. Құрылымдық модельдер жүйелердің құрылымын және оның элементерінің өзараәсерінзерттейді.
.
Құрылымдық модельді оқып үйрену үстінде объектінің мазмұнын туралы, оның сыртқы жағдайларға әсері туралы информацияларды алуға болады. Ал функционалдық модельді зерттегенде объектінің әртүрлі реакцияларының сыртқы ортаға әсері туралы деректер алуға болады. Сонымен қатар объектінің құрылымын талдауға және құрылымдық модельдерді құруға мүмкіндіктер туады.
Экономикалық-математикалық модельдер жүйе жағдайын болашақты жоспарлау мен болжауға пайдаланады. Мұндай жағдайда модель оның негізінде қойылған белгілі бір алғы шарттарға сәйкес экономикалық үрдістердің ағымын кӛрсетеді. Жоспарлауменболжау модельдерінде алғышарттарды дұрыс таңдау ерекше маңызды роль атқарады. Модель есептің шарты дұрыс қойылған кезде ғана нақты жүйелердің құрылысы мен функциясын дұрыс сипатайды.
Экономикалық-математикалық модельдер сипаттаулы және оптималды болып бөлінеді.
Экономикалық жүйелердің сипаттаулы моделі есептерді математикалық формула түрінде көрсетеді және жүйе жағдайымен оның элементтерінің байланысын тереңірек ұғып үйренуге қолданылады.
және экономикалық аудандардың салааралық байланысының матрицалық моделі жатады. Осындай типті есептің модельдері анықталған алғашқы мәліметтері бойынша бір ғана шешімі болады. Бұл модельдердің негізгі кемшілігі - ең тиімді (оптималды) шешімін іздейтін шарттың жоқтығы.
Оптималды модельдерде экономикалық есептің мағынасы математикалық формула түрінде жазылады және ең тиімді шешімі табылатын шарт функция түрінде кӛрсетіледі.
критерийіне сәйкес тиімді шешім алуға мүмкіндік береді. Мұндай модельдерге , кесіп-пішудіоптималдау, , , .
Оптималдық модельдердің көпшілігінде оптиалдықтың бірғана критерийі қарастырылады.
Математикалық модельдерде сызықтық және сызықтық емес тәуелділіктердің әртүрлі түрлері қолданылады.
Математикалық модельдеу үрдісінің негізгі бөлігіаппроксимация (жуықтау) - математикалық амалдарды (функция, теңдеу т. с. с. ) басқа қарапайым шамалар арқылы жуықтап табу болып табылады. Аппроксимацияның , сызықтық емес теңдеулерді сызықтық теңдеулерге келтіреді.
Модельденетін обьектінің белгілі бір уақытқа немесе уақыт аралығына сәйкес қасиеттерін сипаттайтын математикалық модельдер статикалық деп аталады.
Математикалық модельді құрастырудың жалпы реттілігі.
Халық шаруашылығы мен білім салаларында электронды есептеу машиналарының кеңінен қолданылуының басты себебі - жалпы технологиялар мен есептеу техникаларының қарқынды дамуы негізінде инженерлік зерттеу жұмыстарында математикалық әдістердің кеңінен қолданылуы екені белгілі.
Практикалық есептерді ЭЕМ-де шешу бастапқы берілгендер мен есептің мақсатын математикалық тілде сипаттаудан басталады. Есепті шешу шарттары мен мақсаттарын математикалық таңбалармен заңдылықтар жиынтығында дәл белгілеу. Есептің математикалық қойылымы алдымен есептің математикалық моделін құрылуымен, сонан соң есепті шешу тәсілі талданып сәйкес алгоритм құрылады. Математикалық модельдеу нақты дүниедегі обьекттер мен процестерді олардың математикалық тілдегі жуықталған сипаттамалары болған - математикалық модельдері - жәрдемінде зерттеу әдісі болып табылады. Бұл әдіс өте кең қолданыс тапқан, амалда ғылымда, басқа да қолданбалы салаларда бірнеше ғасырлардан бері қолданылып келеді. Математикалық модельдеудің мүмкіндіктері мен оның ғылыми-техникалық прогреске әсері соңғы 35-45 жылдың ішінде компьютердің пайда болуы мен оның барлық салаларда қарқынды қолданылуымен ерекшеленеді.
Математикалық модельді құру процесін шартты түрде бірнеше кезеңге бөлуге болады:
1. Математикалық модельді құру.
2. Сәйкес есептеу есептерінің қойылымы, оларды зерттеу және шешу .
3. Практикада модель сапасын тексеру және модельді жетілдіру.
Қолданбалы есептерді компьютер көмегімен шешу кезеңдерін бірнеше кезеңге бөлуге болады.
1. Мәселенің қойылымы.
2. Математикалық модельді таңдау немесе құру.
3. Есептеу есебінің қойылымы.
4. Есептеу есебінің қасиеттерін алдын ала талдау.
5. Сандық әдісті таңдау немесе құру.
6. Алгоритмдеу және программалау.
7. Программаны отладка (дұрыстау) жасау.
8. Программа бойынша есептеулер жүргізу.
9. Нәтижелерді өңдеу және интерпретация жасау.
10. Нәтижелерді пайдалану және математикалық модельді түзету.
Математикалық модельді құру және қолданбалы есептерді компьютер көмегімен шешуде үлкен көлемдегі жұмыстарды орындауға тура келеді. Есептеу экспериментінде есептеулер нақты обьектпен емес, оның математикалық моделімен жүргізіледі, тәжірибелік қондырғы орнын компьютер атқарады. Компьютер арнайы құрылған қолданбалы программалар пакетімен (ҚПП) жабдықталған болады. Сондықтан, ғылыми-техникалық және қолданбалы есептерді кешенді шешуді есептеу эксперименті ретінде жүргізген дұрыс.
Математикалық модельдеуде компьютерлердің кең қолданылуы, құрылған теория және алынған елеулі практикалық нәтижелер есептеу экспериментін ғылыми және қолданбалы зерттеулердегі жаңа технология мен әдістеме деп атауға болады.
Есептеу экспериментінің натуралық эксперименттерден артықшылық жақтарына тоқтала кетейік. Әдетте, есептеу эксперименті физикалық эксперименттен арзан болады. Бұл экспериментке жеңіл және қауіпсіз араласуға болады. Оны бірнеше рет қайталауға болады, сондай-ақ кез келген уақытта тоқтатуға болады. Эксперимент кезінде лабораториялық жағдайда келтіріп шығару мүмкін болмаған жағдайларды модельдеу мүмкін. Есептеу экспериментінің негізгі кемшілігі оның нәтижелерін қолдану мүмкіншілігі қабылданған математикалық модель шеңберінде ғана болады.
Барлық модельдер және модельдеу түрлерінің ортасында бізге маңыздысы математикалық модель мен математикалық модельдеу түсініктері.
Әр қарай ақпаратты түсіну үшін кейбір түсініктерді анықтайық.
Математикалық модель дегеніміз - математикалық қатынастар түрінде жазылған, техникалық объект немесе құбылыс туралы білімдердің, ұсыныстардың және ғылыми болжам жиынтығы.
Математикалық модельдеу дегеніміз - математикалық модельге кіретін теңдеулерді аналитикалық, сандық (ЭЕМ-да), немесе аналогтық (АЕМ) шешу жолымен оның математикалық моделі бойынша объектіні немесе құбылысты зерттеу процесі.
Математикалық модельдеудің түрі - имитациялық модельдеу.
Зерттеу объектілері (ЗО) - электр жетегімен қимылға келтірілетін машиналар, механизмдер, технологиялық желілер, сондай-ақ осы жүйелердің элементтері: автоматтық реттеуіштер; түзеткіш буындары; сүзгілер; сигналдарды беру және шектеу блоктары; датчиктер; жеке электр тізбектері [1] .
Физикалық құрылғысына қарамай кез келген құрылғыларды жобалау кезіндегі кейбір жалпы түсініктерді айтып кетейік.
Жобалау құрылғысының элементтерінің параметрлері - ішкі параметрлер деп аталады. Құрылғының жұмыс істеу сапасын бағалайтын параметрлері - шығыс параметрлері деп аталады. Сыртқы ақпараттық сигналдарының құрылғыға әсер беретін параметрлері - кіріс , ал қоршаған ортаның параметрлері - сыртқы параметрлері деп аталады [1] .
Кез келген зерттеу объектісін "қара жәшік" ретінде қарастыруға болады.
"Қара жәшік" - ол объектінің кіріс және шығыс параметрлерін талдау мүмкінділігі бар зерттеу әдісі.
"Қара жәшік" ретінде көрсетілген зертеу объектісін графикалық түрде 4. 1. суретте көруге болады.
Сонымен, зерттеу объектісі кіріске келген сигналдарды әр түрлі математикалық модельдер бойынша түрлендіреді. Мысалы, зертеу объектісі:
- дифференциал теңдеу арқылы немесе операторлы түрде;
- беріліс функциясы ретінде;
- теңдеулер тағы да басқа түрде жазылуы мүмкін.
Операторлы түрде жазу үшін, теңдеулерге келесі тік алмастыруды қолдану керек:
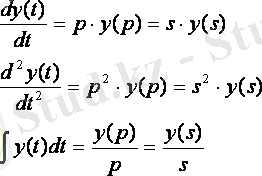
(4. 1)
(4. 2)
(4. 3)
Осындай алмастыру Лаплас түрлендіру деп аталады. P және s әріптер бір ұғымды білдіріп - Лаплас операторы деп аталады. (4. 1), (4. 2) және (4. 3) формулалар тікелей алмастыруын көрсетеді. Лаплас түрлендірулері дифференциал теңдеулерін қарапайым алгебралық теңдеулер түрінде келтіруге болдады, оларды шешу оңай болады және оларды беріліс функцияларын жазу түрінде қолданады.
Беріліс функциясы - Лаплас бейнелеуі шығыстың кіріс сигналының қатынасы болып табылады [2] . 4. 1 суретте көрсетілген сұлбаның беріліс функциясын келесі түрде жазуға болады:
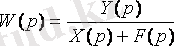
... жалғасы
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz