Жазықтықтағы аналитикалық геометрия және түзулер теориясының негіздері


Жазықтықтағы аналитикалық геометрия элементтері. Түзулер теориясы
Мазмұны:
Кіріспе
1 тарау. Жазықтықтағы аналитикалық геометрия
1. 1 Жазықтықтағы аналитикалық геометрияның элементтері
1. 2 Аналитикалық геометрия
1. 3 Аналитикалық геометрия негіздері.
2 тарау. Түзулер теориясының сипаттамасы
2. 1 Жазықтықтағы түзудің берілу тәсілдері
2. 2 Түзулер теориясы
Қорытынды
Әдебиеттер тізімі
Кіріспе
X, y, z координаттарына қатысты бірінші дәрежелі кез келген теңдеулер
+ By + Cz +D = 0 жазықтықты анықтайды және керісінше: әр жазықтықты жазықтықтың теңдеуі деп аталатын теңдеумен ұсынылуы мүмкін.
N (A, B, C) векторы, ортогональды жазықтықтың қалыпты векторы деп аталады. A, B, C коэффициенттері теңдеуінде бір мезгілде 0 тең емес. Теңдеудің ерекше жағдайлары
D = 0, Ax+By+Cz = 0 - жазықтығы координаттардың басы арқылы өтеді.
C = 0, Ax+By+D = 0 - жазықтығы Oz осіне параллель.
C = D = 0, Ax +By = 0 - жазықтығы Oz осінен өтеді.
B = C = 0, Ax + D = 0-жазықтығы Oyz жазықтығына параллель.
Координаттық жазықтықтардың теңдеулері: x = 0, y = 0, z = 0.
Кеңістікте тікелей берілуі мүмкін:
) екі жазықтықтың қиылысу сызығы ретінде, яғни теңдеулер жүйесі:
A1 x + B1 y + C1 z + D1 = 0, A2 x + B2 y + C2 z + D2 = 0;
1) екі нүктесімен M1(x1, y1, z1) және M2(x2, y2, z2), онда түзу, олар арқылы өтетін, теңдеулермен беріледі:
нүкте M1(x1, y1, z1), оған тиесілі, және векторы a (m, n, р), оған коллинеарным. Сонда түзу теңдеулермен анықталады:
Теңдеулер канондық түзулер деп аталады.
A векторы түзу векторы деп аталады.
Түзудің параметрлік теңдеулері әр қатынасты t параметріне теңестіреміз:
= x1 +mt, y = y1 + nt, z = z1 + рt.
Жүйені X және y белгісіз сызықтық теңдеулер жүйесі ретінде шеше отырып, проекциялардағы түзу теңдеулеріне немесе келтірілген түзу теңдеулеріне келеміз: mz + a, y = nz + b
Әр теңдеуден z тауып және алынған мәндерді теңестіре отырып, теңдеулерден канондық теңдеулерге өтуге болады:
Егер осы түзудің қандай да бір нүктесін және оның бағыттаушы векторын N = [n1, n2], мұндағы n1(A1, B1, C1) және n2(a2, B2, C2) -берілген жазықтықтардың қалыпты векторлары. Егер теңдеулердегі m, n немесе р бөлгіштерінің бірі (3. 4) нөлге тең болса, онда тиісті бөлшек санын нөлге тең етіп қою керек, яғни жүйе
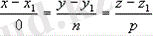
жүйеге тең
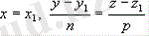 мұндай тікелей Ох осіне перпендикуляр.
мұндай тікелей Ох осіне перпендикуляр.
Жүйесі
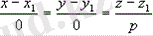 жүйеге тең x = x
1
, y = y
1
; тікелей Oz осіне параллель.
жүйеге тең x = x
1
, y = y
1
; тікелей Oz осіне параллель.
Курстық жұмыстың мақсаты : кеңістіктегі түзу және жазықтықты оқып үйрену.
Курстық жұмыстың міндеттері: кеңістіктегі жазықтықты, оның теңдеуін қарастыру, сонымен қатар кеңістіктегі жазықтықты қарастыру.
Курстық жұмыс құрылымы: кіріспе, 2 тарау, қорытынды, қолданылған әдебиеттер тізімі.
1 тарау. Жазықтықтағы аналитикалық геометрия
1. 1 Жазықтықтағы аналитикалық геометрияның элементтері
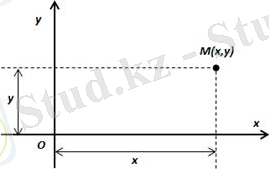
Тік бұрышты координаталар системасындағы нүктенің координаталары. Кесіндіні берілген қатынаста бөлу
Аналитикалық геометрия геометриялық бейнелерді алгебралық әдістермен зерттейді. Аналитикалық геометрияның негізгі құралы XVII ғасырда Декарт енгізген координаталар әдісі болып табылады.
О нүктесінде қиыласатын, кесінділерді өлшеу бірліктері бірдей болатын өзара перпендикуляр екі Ох, Оу түзуді тік бұрышты координаталар системасы деп атайды. Ох осін абсцисса осі деп, Оу осін ордината осі деп атайды.
Тік бұрышты координаталар системасын кейде Декарттық координаталар системасы деп те айтады. Оху координаталар системасында берілген М нүктесінің координаталары х, у ( х, у сандары суретте көрсетілген кесіндінің ұзындықтары арқылы анықталады) сандары болса, онда ол нүктені М(х; у) деп белгілейміз. Мұнда х -нүктенің абсциссасы, у - нүктенің ординатасы.
Декарттық координаталар системасында М 1 (х 1 ; у 1 ), М 2 (х 2 ; у 2 ) нүктелері берілсін. Олардың ара қашықтығы төмендегі формуламен есептеледі:
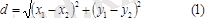
Бір түзудің бойында жатпайтын үш нүкте үшбұрыш анықтайтынын мектеп курсынан білеміз.
Теорема. Бір түзудің бойында жатпайтын кез-келген үш нүкте А(х 1 ; у 1 ), В(х 2 ; у 2 ) , С(х 3 ; у 3 ) анықтап тұрған үшбұрыштың ауданы мына формуламен есептеледі:
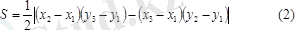
(2) формуланы, есте сақтауға ыңғайлырақ мына түрде жазуға болады:
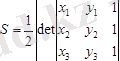 (сыртқы тік жақша абсолют шаманың белгісі) .
(сыртқы тік жақша абсолют шаманың белгісі) .
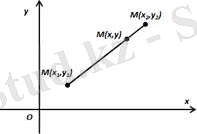 Айталық, жазықтықта
М
1
М
2
кесіндісі берілсін,
М
осы кесіндінің кез-келген
М
2
- ден басқа нүктесі болсын.
М
нүктесі
М
1
М
2
кесіндісін
λ
қатынасында бөліп тұрсын, яғни:
Айталық, жазықтықта
М
1
М
2
кесіндісі берілсін,
М
осы кесіндінің кез-келген
М
2
- ден басқа нүктесі болсын.
М
нүктесі
М
1
М
2
кесіндісін
λ
қатынасында бөліп тұрсын, яғни:
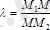
М 1 (х 1 ; у 1 ), М 2 (х 2 ; у 2 ) нүктелері анықтап тұрған кесіндіні λ қатынасында бөлетін М(х; у) нүктесінің координатасын төмендегі формулалар арқылы есептеуге болады:
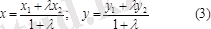
λ=1 болғанда кесіндінің ортасы болып тұрған нүктенің координатасын табатын формула шығады:
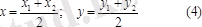
 Кей жағдайларда Декарттық координаталар системасынан басқа координаталар системасын қолдану ыңғайлырақ болады. Сондай координаталар системасының бірі - полярлық координаталар системасы.
Кей жағдайларда Декарттық координаталар системасынан басқа координаталар системасын қолдану ыңғайлырақ болады. Сондай координаталар системасының бірі - полярлық координаталар системасы.
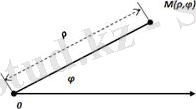
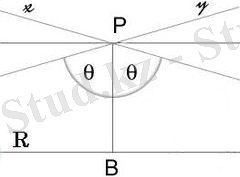
Полярлық координаталар системасында М нүктесі полюс деп аталатын О нүктеден қашықтығы (ОМ=ρ) мен ОМ кесіндінің полярлық ось деп аталатын ОЕ түзуімен жасайтын бұрышы φ арқылы анықталады. ОМ кесіндісін нүктенің полярлық радиус-векторы деп атайды. Егер полярлық осьтен полярлық радиус-векторға қарай бұрылу бағыты сағат тіліне қарсы бағыт болса, онда бұл бұрыш оң таңбалы болады, кері бағытты теріс бағыт деп есептейді.
Нүктенің декарттық координаталары мен полярлық координаталары арасында мынадай байланыс бар (полярлық осьті абсцисса осі деп есептейміз, ал ордината осі полярлық осьпен оң бағытта 90 градус бұрыш жасайды) .
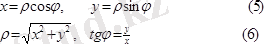
Q жазықтығы жалпы түрдегі теңдеумен берілсін: Ax + By + Cz + D=0, ал параметрлік түрде түзу L: x=x1+mt, y=y1+nt, z=z1+pt, сонда түзудің L және Q жазықтығының қиылысу нүктесін табу үшін, түзудің нүктесі жазықтықта жатқан t параметрінің мәнін табу керек. Подставив мәні x, y, z, қр теңдеуі жазықтықта және білдіре отырып, t, аламыз
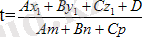
T мәні түзу және жазық параллель болмаса, жалғыз болады.
Түзудің және жазықтықтың параллельдік және перпендикулярлығының шарттары
Тікелей l қарастырайық:
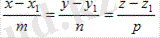
және α жазықтығы:
+By + Cz + D=0.
Түзу L және α жазықтығы:
а) түзу векторы және коллинеарлы жазықтықтың қалыпты векторы бір-біріне перпендикуляр, яғни.
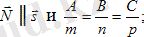
б) векторлар мен перпендикуляр болғанда бір-біріне параллель болады, яғни.
және Am + Bn + Ср = 0.
түзу және жазықтықтың арасындағы бұрыш
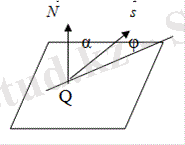
Жазықтықтың қалыпты векторы мен түзудің бағыттаушы векторы арасындағы α бұрышы мынадай формула бойынша есептеледі:
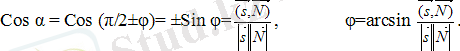
Жазықтық шоғыры
Берілген түзу L арқылы өтетін барлық жазықтықтардың жиынтығы жазықтықтар шоғыры деп аталады, ал түзу l - шоғыр осі. Будың осі теңдеулермен берілсін
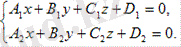
Жүйенің екінші теңдеуін тұрақты және бірінші теңдеумен қосамыз:
A1x+B1y + C1z+D1 + λ (A2x+B2y+C2z+D2) =0.
Бұл теңдеудің бірінші дәрежесі х, у, z және сәйкесінше, λ кез келген сандық мәнде жазықтықты анықтайды. Бұл теңдеулер екі теңдеудің салдары болғандықтан, осы теңдеулерді қанағаттандыратын нүкте координаттары осы теңдеуді да қанағаттандыратын болады. Демек, λ кез келген сандық мәнде берілген теңдеу берілген түзу арқылы өтетін жазықтықтың теңдеуі бар. Алынған теңдеу-жазықтықтар шоғырының теңдеуі.
Мысал. Параллель М1(2, -3, 4) нүктесі арқылы өтетін жазықтықтың теңдеуін жазу
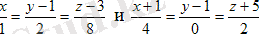
Шешімі. Осы М1 нүктесі арқылы өтетін жазықтықтар байламының теңдеуін жазамыз:
А (х-2) + В (у + 3) + C(z - 4) = 0.
Ізделіп жатқан жазықтық деректерге параллель болуы тиіс болғандықтан, оның қалыпты векторы осы түзулердің бағыттаушы векторларына перпендикуляр болуы тиіс. Сондықтан N векторы ретінде векторлардың векторлық көбейтіндісін алуға болады :
Демек, А = 4, В = 30, С = - 8. А, В, С табылған мәндерін жазықтықтың байланыстырғыш теңдеуіне
1. 2 Аналитикалық геометрия
Аналитикалық геометрия - геометрияның қарапайым геометрия бейнелерді (түзулер, жазықтықтар, қисықтар, екінші реттік беттер) координаттар әдістерінің негізінде алгебралық амалдар арқылы зерттейтін бөлімі.
Координаттар әдісінің пайда болуы 17 ғ-да астрономия, механика және техника ғылымдарының дамуымен тығыз байланысты. Координаттар әдісі мен аналитикалық геометрияның негіздері Р. Декарттың «Геометриясында» (1637) мейлінше толық және анық баяндалған. Бұл әдістің басты идеялары оның замандасы П. Фермаға да белгілі болған. Аналитикалық геометрияның бұдан әрі дамуына Г. Лейбниц, И. Ньютон және Л. Эйлер зор үлес қосқан. Аналитикалық геометрияның тұжырымдарын Ж. Лагранжаналитикалық механика, ал Г. Монж дифференциалдық геометрия негіздерін қалау барысында пайдаланған.
Координаттар әдісінің мәні - жазықтықта орналасқан кез келген
М(х, у)
нүктесін декарттық координаттар жүйесі арқылы анықтауға болатындығында. х және у шамалары Оху жүйесіндегі М нүктесінің декарттық тік бұрышты координаттары (не қысқаша тік бұрышты координаттар) деп аталады. Осыған сәйкес оларды М нүктесінің абсциссасы (х) және ординатасы (у) деп атайды.
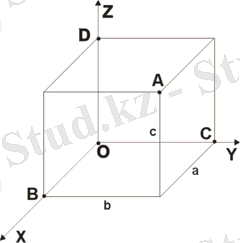
Жазықтықтағы координаттар әдісінің негізгі идеясы - L сызығының геом. қасиеттерін осы сызықты сипаттайтын Ғ (х, у) = 0 теңдеуін аналит. және алгебр. жолмен зерттеу. Жазықтықтағы А. г-да 1- және 2-реттік алгебр. сызықтар жүйелі түрде зерттеледі. 1-реттік сызықтар - түзу сызықтар және олар бір дәрежелі Ах + Ву + С = 0 алгебр. теңдеуімен, ал 2-реттік қисық сызықтар Ах2 + Вху + Су2 + Dх + Еу + Ғ = 0 теңдеуімен сипатталады. 2-реттік қисық сызықтарға эллипс, гипербола, парабола қисықтары жатады. Табиғатта өте жиі кездесетін бұл қисықтардың негізгі қасиеттері А. г-да толық анықталған. Кеңістіктегі А. г-да координаттар әдісі жазықтықтағы әдіске толық ұқсас етіп қарастырылады. Мұнда кез келген М нүктесі х - абсцисса, у - ордината және z - аппликата координаттары арқылы анықталады. Кеңістікте орналасқан S бетін Oxyz координаттар жүйесіне қатысты F = (x, y, z) = 0 теңдеуімен сипаттауға болады. Кеңістіктегі А. г-да Ах + Ву + Сz + D = 0 теңдеуімен анықталатын 1-реттік беттердің (жазықтықтардың) және Ах2 + Ву2 + Сz2 + Dху + Еуz + Ғхz + Gх + Ну + Мz + N = 0 теңдеуімен анықталатын 2-реттік беттердің (эллипсоидтың, гиперболоидтың, параболоидтың) қасиеттері зерттеледі.
Қазақстанда аналитикалық геометрияның дамуына профессорлар А. З. Закарин, Ф. Д. Крамер, В. В. Стрельцов, доценттер С. А. Аяпбергенов, М. У. Исқақов, Ж. Ш. Юсупов, Э. И. Хмелевский, т. б. айтарлықтай үлес қосты.
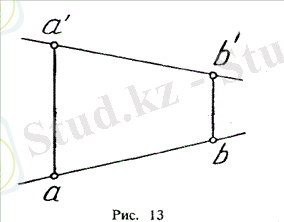
Кеңістіктегі түзу сызық шексіз, сондықтан оны ыңғайлы бөлікке қою. Евклидтік геометрияның мектеп курсынан аксиома белгілі, "кеңістіктегі екі нүктеден кейін тура және, притпен тек бір ғана өткізуге болады". Демек, эпюрде түзу екі фронтальды және екі көлденең нүкте проекциясымен берілуі мүмкін. Бірақ түзу - бұл тік (қисық емес) болғандықтан, біз осы нүктелерді түзу сызықпен қосып, тік және көлденең проекцияларды ала аламыз (сурет. 13) .
Кері дәлел: V және Н проекцияларының жазықтығында а' b' және ab екі проекциялары берілген (сурет. 14) . Олар арқылы V және Н проекцияларының жазықтықтарына перпендикуляр жазықтықтарды жүргіземіз (сурет. 14), жазықтықтардың қиылысу сызығы түзу АВ болады.
Кеңістіктегі түзудің әртүрлі жағдайлары
Біз қарастырған жағдайларда түзу параллель емес, V, н, W проекцияларының жазықтықтарына перпендикуляр болған жоқ. Олар жоғары немесе төмен болуы мүмкін (өзін түсіну) .
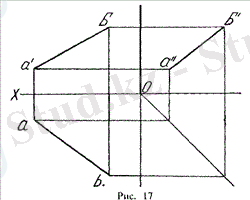
Сур. 17 үш проекциямен берілген жалпы жағдайды тікелей көрсетеді. Маңызды қасиеттері бар түзу, проекцияның қандай да бір жазықтығына параллель түзулер отбасын қарастырайық.
Сур. 17 үш проекциямен берілген жалпы жағдайды тікелей көрсетеді.
Маңызды қасиеттерге ие түзу, проекциялардың қандай да бір жазықтығына параллель түзулер отбасын қарастырайық.
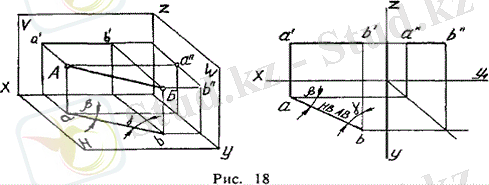
а) көлденең тік (әйтпесе - көлденең, тік көлденең деңгей) . Бұл проекцияның көлденең жазықтығына параллель түзу деп аталады. Оның кеңістіктегі және эпюрадағы бейнесі 18 суретте көрсетілген.
Көлденең "бетке" эпюрасында білу оңай: оның алдыңғы проекциясы әрдайым ОХ осіне параллель. Горизонтальдың толық маңызды қасиеті осылай қалыптасады:
Көлденең-алдыңғы проекция ОХ осіне параллель, ал көлденең табиғи шаманы көрсетеді. Эпюрадағы көлденең көлденең проекция оның V жазықтығына (B бұрышы) және W (у) жазықтығына көлбеу бұрышын анықтауға мүмкіндік береді - сурет. 18.
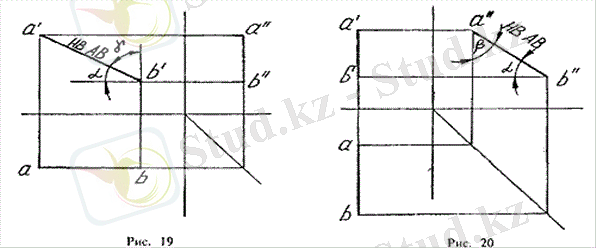
б) фронтальды тік (фронталь, фронтальды деңгей) - бұл проекцияның фронтальды жазықтығына параллель түзу, параллель. Біз оны көрнекі бейнемен суреттемейміз, оның эпюрасын көрсетеміз (сурет. 19) .
Эпюр фронталь көлденең және профильді оның проекциялары X және Z осьтеріне сәйкес параллель, ал фронтальды проекция ерікті түрде орналасады және фронтальдың табиғи шамасын көрсетеді. Эпюрада жолай көлденең (а) және проекциялардың бейінді (у) жазықтықтарына тік көлбеу бұрыштары бар. Сонымен, тағы бір рет:
Фронтальда-көлденең проекция ОХ осіне параллель, ал фронтальды табиғи шаманы көрсетеді
в) бейіндік түзу. Әлбетте, бұл проекциялардың түзу, бейінді жазықтығына параллель (сурет. 20) . Сондай-ақ, Профильді түзудің табиғи шамасы проекцияның Профильді жазықтығында (а"b" проекциясы-сурет. 20) және мұнда оның көлбеу бұрыштарын Н (a) және V (b) жазықтықтарына көруге болады.
Келесі тікелей отбасы, бірақ тікелей деңгей ретінде маңызды емес, бұл проекциялаушы тікелей.
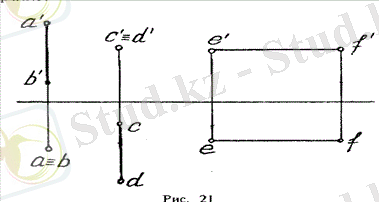
Проекциялар жазықтығына перпендикуляр түзу проекциялар деп аталады (проекциялаушы сәулелерге ұқсас-сурет. 21) .
АВ пл. Н - тік көлденең-проекциялайтын; пл. V - тік фронтальды-проекциялайтын; пл. W - тік бейінді-проекциялайтын.
1. 3 Аналитикалық геометрия негіздері.
Түзу геометриядағы алғашқы ұғымдардың (түсініктердің) 6ipi.
Бізге: екі нүкте арқылы жалғыз түзу жүргізуге болатыны; түзу бойында жатқан нүкте арқьлы осы түзуге перпендикуляр жалғыз түзу жүргізуге болатыны т. с. с. аксиомалар белгілі.
Мектеп курсынан L түзуінің тендеуі
y = kx + l (1. 1)
түрінде жазылатынын білеміз. Мұнда
k = tg
 -
түзудің бұрыштық коэффициенті,
ал
-
түзудің бұрыштық коэффициенті,
ал
 L -
түзуі мен
х-
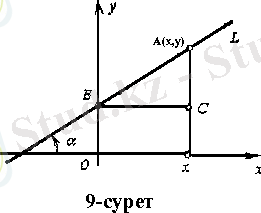
өсінің оң бағаты арасындағы бүрыш; l - түзу мен y
ө
сінің киылысу нүктесінің ординатасы
(1 = ОВ)
(9 - суретті караңыз) .
L -
түзуі мен
х-
өсінің оң бағаты арасындағы бүрыш; l - түзу мен y
ө
сінің киылысу нүктесінің ординатасы
(1 = ОВ)
(9 - суретті караңыз) .
Ах + Ву + С = 0 (1. 2) .
тендеуін қарастырайык, Мұндағы А, В, С - белгілі сандар және А мен В б ір мезгілде нөлге тең емес.
Егер B≠О болса, онда (1. 2) - ден
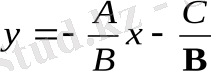 түрінде немесе
түрінде немесе
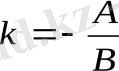 ,
,
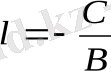 арқылы
белгілеп
y = kx + l,
яғни (1. 1) - теңдеу түрінде
жаза
аламыз.
арқылы
белгілеп
y = kx + l,
яғни (1. 1) - теңдеу түрінде
жаза
аламыз.
Егер В = 0 болса, онда (1. 2) - ден Ах + С = О (А ≠ 0)
немесе
х = а
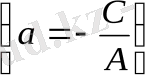 (1. 3)
(1. 3)
түрінде жазуға болады. Бұл
у
өсіне параллель түзу, басқаша айтқанда, абсциссалары
а
санына тең болатын нүктелердің геометриялық орны (16 - суретті к, арацыз) . Егер
А = 0 (В
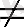 0) болса, онда (1. 2) - ден
0) болса, онда (1. 2) - ден
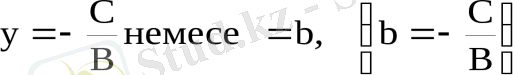 (1. 4)
(1. 4)
түрінде жазар едік. Бұл х өсіне параллель тузу: ординаталары b санына тең болатын нүктелердің геометриялык, орны (1. 3) жене (1. 4) тендеулерінде а = 0 және b = 0 болса, онда х = О және у = 0, сейкес у - өсінің және х- өсінің теңдеулері шығады. (1. 2) - ні жазықтықтағы түзудің жалпы тендеуі деп атайды.
1 - есеп. Бұрыштық коэффициенті k - тең, (х 0 , у 0 ) - нүктесі арқылы ететіп түзу тендеуін жазу керек.
Шешуі. y = kх + l - бұрыштык, коэффициенті k - тең, (l - кез келген сан) болатын түзу теңдеуі. (х 0 , у а ) - осы түзу бойында болатындықтан y o = kх o + l (1. 5)
тендіқ орындалуы тиіс. (1. 1) - тең (1. 5) - ті мүшелеп шегеріп іздеп отырған тендеуді аламыз:
у-у 0 =k(x-x o ) . (1. 6)
2 - есеп. М 1 (х 1 , у 1 ) және М 2 (х 2 , у 2 ) екі нүкте арқылы өтетін түзу тендеуін жазу керек.
х 1 ≠х 2 болсын, онда ізделінген тузу у өсіне параллель емес, сондықтан оның тендеуі ((1. 6) - қараңыз) .
у-у 1 =k(x-x l ), k-сан (1. 7)
түрінде жазылады. Бұл тендеуден түзудің M 1 (х 1 ; x 1 , ) нүктесі арқылы өтетіні керініп тұр. Ол М 2 (х 2 , у 2 ) нүктесі арк. ылы да ететіндіктен
у 2 -у 1 =k(x 2 -x l ), (1. 8 )
тенңдігі орындалуы тиіс. (1. 7) - ні (1. 8) - ге мүшелеп бөлеміз, сонда
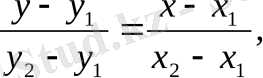 (1. 9)
(1. 9)
берілген M t (x 1 , y 1 ) және М 2 (х 2 , у 2 ) нүктелері арқылы өтеті түзу тендеуін аламыз.
Егер x 1 = х 2 = с болса, онда ізделінген теңдеу х = с түріне ие болады. Бұл жағдайда (1. 9) - тендеу
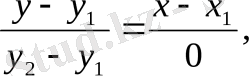 түріне келер еді. Бұл өрнектің мағанасы болмаса да жазуға ыңғайлы мысал мұндағы бөлімдерден құтылсақ
түріне келер еді. Бұл өрнектің мағанасы болмаса да жазуға ыңғайлы мысал мұндағы бөлімдерден құтылсақ
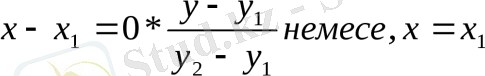 алар едік. Ал у
2
=у
1
жағдайында
алар едік. Ал у
2
=у
1
жағдайында
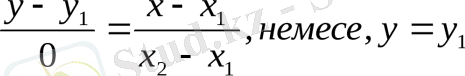
болады.
3 -Есеп. y 1 =k 1 x + l l және у= k 2 х + / 2 түзулерінің арасындағы бұрышын табу керек.
Шешу. k 1 = tgα 1, k 2 = tgα 2 бұрыштык; коэффициенттер, α 1, α 2 түзулердің х- өсінің оң бағытымен жасайтын бұрыштары (10 - суретті караңыз) .
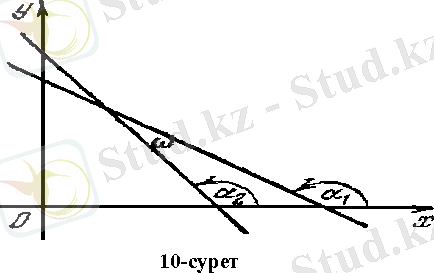
ω = α 1 - α 2 теңдігінен
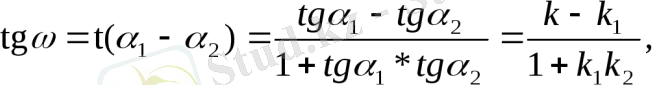 (1. 10)
(1. 10)
яғни екі түзу арасындағы бұрышты табу формуласын аламыз. (1. 10) - теңдіктен екі түзудің перпендикулярлық белгісі
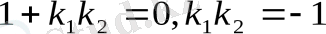 және
екі түзудаң параллельдік
(tga>
= 0) белгісі.
және
екі түзудаң параллельдік
(tga>
= 0) белгісі.
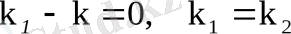 шығады.
шығады.
Жағдайға бейімдеп (1. 2) теңдеуді x = x l , y = x 2 , А = А 1, В = А 2 деп алып
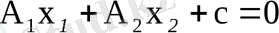 (1. 11) түрінде жазып алайық.
(1. 11) түрінде жазып алайық.
Егер A 1 ≠0, A 2 ≠0, С≠0 болса, онда (1. 11) - ді келесі түрге келтіруте болады:
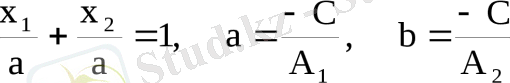 (1. 12)
(1. 12)
(1. 12) - нi түзудін кесіндідегі теңдеуі деп атайды. Бұл түзу х } - өсін (а, 0), ал х 2 - өсін (О, b ) нүктесінде кияды.
(1. 11)
тендеуімен берілген түзу
(
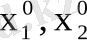 )
нүктесі арқылы ететін болса, онда
)
нүктесі арқылы ететін болса, онда
А 1 Х 1 ° + А 2 х 0 2 +С = 0 (1. 13)
Теңдігі орынадалады. (1. 11) - lен (1. 13) - nі шегерсек, онда келесі тендеуге келеміз:
А
1
(x
1
-x
1
°) + А
2
(x
2
-х
0
2
) = 0
(1. 14) Бұл түзудің
M
0
(x
1
°, х
0
2
)
нүктесі арқылы ететін теңдеуі.
Егер
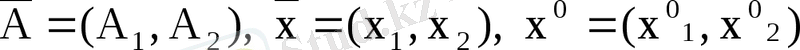 векторларын енгізсек,
векторларын енгізсек,
онда (1. 14) - тің сол жағындағы шама
А
мен
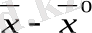 векторларының
векторларының
скаляр кебейтіндісі екенін көрінеді
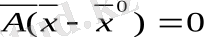 (1. 15)
(1. 15)
Мұндағы
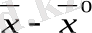 векторы L, түзуінде жатыр
векторы L, түзуінде жатыр
Олай болса, (1. 15) - тен А = (А 1 , А 2 ) векторы берілген түзуге перпендикуляр болатыны шығады. Бұл А 1 , А 2 коэффициенттерінің геометриялық мағынасы.
L түзуше перпендикуляр вектор осы түзудің нормалі (нормаль векторы) деп аталады да оны көбінесе n арқылы белгілейді.
Соньмен, n =(A 1 , A 2 ) ⊥L, яғни L: А 1 х 1 + А 2 х 2 + С = 0 тендеуіндегі A 1 , A 2 осы тузуге нормаль вектордың координаталары болатынын көрдік.
Келесі
L 1 : А 1 х 1 + А 2 х 2 + С = 0
L 2 : B 1 x ] +B 2 x 2 +C 2 =0, түзулерінің арасындағы φ бұрышты табу керек болсын.
А
= (А
1
, А
2
) ⊥
L,
жэне
B
= (B
1
, B
2
)
⊥
L
2
болғандықтан
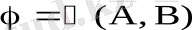 олай болса,
олай болса,
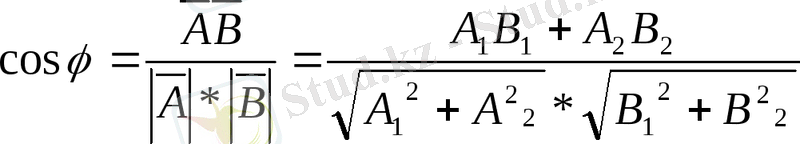 (1. 17)
(1. 17)
(1. 17)
-
ден L
1
және L
2
түзулерінің перпендикулярлык,
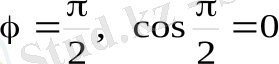 шартын жаза аламыз:
шартын жаза аламыз:
A 1 , A 2 + B 1 , B 2 =0. Егер екі түзу параллель болса (L 1 L 2 ), онда А мен В
коллинеар болады, ягни
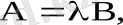 ,
,
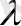 - сан.
- сан.
Бұдан түзулердің параллелдік шарты шығады:
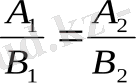
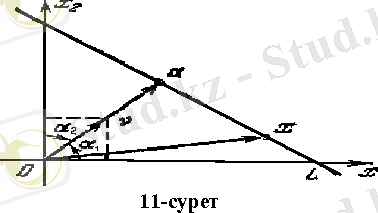
Тік бұрышты координаталар жүйесінде координата бас нүктесінен өтпейтін кез келген l түзуі берілсін. а - координата бас нүктесінен шығатын L түзуіне перпендикуляр, үшы L түзуінде жататын вектор болсын (11-суретті караңыз) .
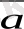 - векторы
l
түзуін толығымен анықтайды, өйткені,
а
-
вектрының ұшы арқылы оған перпендикуляр жалғыз ғана түзу жүргізуге болады.
- векторы
l
түзуін толығымен анықтайды, өйткені,
а
-
вектрының ұшы арқылы оған перпендикуляр жалғыз ғана түзу жүргізуге болады.
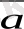 = р,
= р,
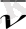 = (cosα
1
, cosα
2
) - а - векторының орты, ал cos α
1
, cos α
2
оның бағыттаушы косинустары болсын.
= (cosα
1
, cosα
2
) - а - векторының орты, ал cos α
1
, cos α
2
оның бағыттаушы косинустары болсын.
x = (x
1
, x
2
) L -
түзуінің кез келген нүктесі (радиус-вектор) болсын. Осы
х
векторының
v -
бірлік векторына проекциясы
р
тең екені айқын нәрсе:
Пр
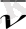
 =
р.
=
р.
Сондықтан, l түзуінің векторлың теңдеуі деп аталатын
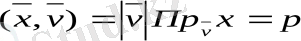 (1. 18)
(1. 18)
тендеуін аламыз. Расында да керісінше (1. 18) - тендеуді қанағаттандыратын әрбір
 нуктесі
l
түзуінде жатады. Егер
l
түзуі координата бас нүктесі арқылы өтсе, онда оның тендеуі де (1. 18) - түрінде жазылады.
нуктесі
l
түзуінде жатады. Егер
l
түзуі координата бас нүктесі арқылы өтсе, онда оның тендеуі де (1. 18) - түрінде жазылады.
(1. 18) -ді координаталар бойынша x [ cosα l +x 2 cosα 2 = р (р≥0), (1. 19)
немесе cos
α
2
=cos(90°-
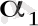 ) = sin
) = sin
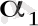 ескеріп
x
1
cosα
1
+x
2
sinα
l
= р
(
р≥0
) (1. 20)
ескеріп
x
1
cosα
1
+x
2
sinα
l
= р
(
р≥0
) (1. 20)
түрінде жазуға болады. (1. 19) немесе (1. 20) - түзудің қалыпты теңдеуі деп аталады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz