Есепті шешу алгоритмі

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 19 бет
Таңдаулыға:

----------------------------------- ----------------------------------- ----------

----------------------------------- ----------------------------------- ----------
Қазақстан Республикасының Білім және ғылым министрлігі
----------------------------------- ----------------------------------- ----------
Қарағанды мемлекеттік техникалық университеті
----------------------------------- ----------------------------------- ----------

----------------------------------- ----------------------------------- ----------

----------------------------------- ----------------------------------- ----------
Ақпараттық есептеуіш жүйелер кафедрасы
----------------------------------- ----------------------------------- ----------

----------------------------------- ----------------------------------- ----------

----------------------------------- ----------------------------------- ----------
КУРСТЫҚ
----------------------------------- ----------------------------------- ----------
ЖҰМЫС
----------------------------------- ----------------------------------- ----------

----------------------------------- ----------------------------------- ----------

----------------------------------- ----------------------------------- ----------

----------------------------------- ----------------------------------- ----------
Автоматтандырылған басқару модельдері мен әдістері пәні бойынша
----------------------------------- ----------------------------------- ----------
(пәннің атауы)
----------------------------------- ----------------------------------- ----------
Тақырыбы: Сызықты емес теңдеуді шешу бағдарламасы
----------------------------------- ----------------------------------- ----------

----------------------------------- ----------------------------------- ----------

----------------------------------- ----------------------------------- ----------

----------------------------------- ----------------------------------- ----------

----------------------------------- ----------------------------------- ----------
Қабылдаған:
----------------------------------- ----------------------------------- ----------

----------------------------------- ----------------------------------- ----------
______________ аға оқытушы Сүлеймен А.Е.
----------------------------------- ----------------------------------- ----------
(баға) (аты-жөні)
----------------------------------- ----------------------------------- ----------
_____________________________ (қолы) (күні)
----------------------------------- ----------------------------------- ----------

----------------------------------- ----------------------------------- ----------

----------------------------------- ----------------------------------- ----------
Комиссия мүшелері: Орындаған:
----------------------------------- ----------------------------------- ----------

----------------------------------- ----------------------------------- ----------
______________________ ИС 17-1 тобы Жумабаев Қ.Б.
----------------------------------- ----------------------------------- ----------
(қолы, аты-жөні) (аты-жөні)
----------------------------------- ----------------------------------- ----------

----------------------------------- ----------------------------------- ----------
(қолы, аты-жөні) (қолы) (күні)
----------------------------------- ----------------------------------- ----------

Карағанды 2020
Қазақстан Республикасының білім және ғылым министрлігі
Қарағанды мемлекеттік техникалық университеті

Факультет ИТФ БЕКІТЕМІН
Кафедра АЕЖ АЕЖ кафедра меңг. м.а. Калинин А.А.
______________ (қолы)
___________2020ж.

КУРСТЫҚ ЖҰМЫСҚА ТАПСЫРМА

Автоматтандырылған басқару модельдері мен әдістері пәні бойынша
ИС-17-1 тобының студенті Жумабаев Қанат Болатұлы
Тақырып: Сызықты емес теңдеуді шешу бағдарламасы
Бастапқы мәліметтері: Курстық жобаның әдістемелік нұсқаулығы.

Тапсырма берілді 28 қаңтар 2020ж.
Жетекші: Сүлеймен А.Е. қолы_________
Студент: Жумабаев Қ.Б. қолы

Мазмұны

Кіріспе 3
1 Теориялық бөлім 4
1.1 Бағдарламалық құралдарға шолу 4
1.2 Тапсырманы қою 4
1.3 Математикалық модель 5
1.4 Есепті шешу алгоритмі 8
1.5 Қойылған міндетті шешу алгоритмінің блок-схемалары 9
2 Тәжірибелік бөлім 12
2.1 Delphi-де қойылған тапсырманы шешу 12
2.1.1 Delphi ортасындағы бағдарлама интерфейсін сипаттау 12
2.1.2. Бағдарламада қолданылған сәйкестендіргіштердің тізбесі 12
2.1.3 Негізгі модульдердің мәтіндері және қосымша нысандарының түр. 12
2.1.4 Нәтижелерді графикалық ұсыну 13
2.2 Қойылған міндетті MathCad құралдарымен шешу 14
2.2.1 Бағдарламада қолданылған сәйкестендіргіштердің тізбесі 14
2.2.2 MathCad бағдарламасының мәтіндері 14
2.2.3 Нәтижелерді графикалық ұсыну 14
2.3 Алынған нәтижелерді талдау 15
Қорытынды 17
Пайдаланылған әдебиеттер тізімі 18
Қосымша 19

Кіріспе

Нақты есептерді шешу үшін компьютерлерді қолдану адамнан бағдарламалау негіздерін білуді талап етеді. Оны игерудегі маңызды кезеңдердің бірі объектілі-бағытталған бағдарламалау негіздерін зерделеу болып табылады.
ООП-қосымшаларды құру кезінде жүйе компоненттерінің арасындағы өзара байланыс үшін объектілерді пайдаланатын бағдарламалау тәсілі.
Объектілі-бағытталған бағдарламалау немесе ООП (object-oriented programming) - әр қайсысы белгілі бір типті жүзеге асыру болып табылатын, хабар жіберу механизмін және мұра иерархиясында ұйымдастырылған кластарды пайдаланатын, бағдарлама жиынтығы түрінде ұсынуға негізделген бағдарламалау әдіснамасы. Бірнеше практикалық есептерді шешу үшін есептеудің дәл әдістерін қолдану пайда болған есептеулерге байланысты қолайсыз болып табылады. Бұл үшін сандық әдістер қолданылады, олар нақты затты оңайлату және оны физикалық модельмен ауыстыру арқылы тек берілген дәлдік дәрежесімен есептеулерді жүргізуге мүмкіндік береді.
Жұмыстың мақсаты тізбекті жақындау, Ньютон, кесіндіні екіге бөлу әдістерімен сызықты емес теңдеулерді шешу алгоритмдерін әзірлеу болып табылады.
Бұл жобада хорд әдістерімен теңдеудің шешімін алу үшін, сонымен қатар кесінді жартысына бөлу үшін Delphi (Embarcadero RAD Studio 2010 әзірлеу ортасына кіретін заманауи іске асыру), Mathcad сияқты пакеттер пайдаланылады. Блок-схемаларды орындау үшін MicrosoftVisio 2010 бағдарламасы қолданылады.

1 Теориялық бөлім
Бағдарламалық құралдарға шолу

Delphi-бұл көптеген кластар (объектілер) және белгілі бір тәуелділіктер бар, ол іске асырылған және пайдалануға дайын, бұл қосымшаларды әзірлеуді жеңілдетуге көмектеседі. Бірақ шаблондардың Объектілік моделіндегі ең маңызды тәуелділіктер: кластарды мұраға алу, виртуалды (virtual) және абстраткалық (abstract) әдістер, қорғалған (protected) және жалпыға қол жетімді (public) әдістерді пайдалану болып табылады. Сонымен қатар, әр түрлі деңгейдегі есептерді шешу үшін өте ыңғайлы болып табылады, өйткені бағдарламалық кодтың көмегімен тек қана үлкен дәлдікпен ғана емес, сонымен қатар табуланған функцияға арналған аппроксимациялайтын полиномдардың (көпмүшелердің) коэффициенттерін табуға және қолданушыға ыңғайлы интерфейсін жасауға мүмкіндік береді. Сондықтан әзірлеудің бұл ортасы өндірісте да, оқу орындарында да, ғылыми мекемелерде да кеңінен қолданылады. Mathcad математикалық пакеті теңдеулер жүйесін және қарапайым теңдеулерді шешуге, сондай-ақ кестеленген функцияға арналған аппроксимациялайтын полиномдардың (көпмүшелердің) коэффициенттерін табуға мүмкіндік береді, бірақ ол Delphi-ден ерекшеленеді, бұл тапсырманы едәуір жеңілдетеді.
MicrosoftVisio пакеті диаграммаларды, соның ішінде блок-схемаларды жылдам және сапалы құруға мүмкіндік береді, сондай-ақ MicrosoftWord-мен үйлесімділікке ие.

Тапсырманы қою

Тапсырма 1, нұсқа 7:
1. Өз нұсқасына сәйкес теңдеудің түбірін графикалық түрде бөлу. А параметрін таңдау арқылы, теңдеудің кем дегенде 3 тамырына ие болатындай етіп өз бетінше қою. А параметрінің қандай мәндерінде теңдеудің 1, 2 және 3 тамыры бар екенін анықтау. Егер теңдеуде көрсетілген тамыр саны болмаса (1,2,3), неге түсіндіріңіз.
2. Жартылай бөлу, хорд, жанама әдістерімен теңдеудің тамырын нақтылау алгоритмдерін әзірлеу және алгоритмдердің блок-сызбасын құру.
3. Pascal (немесе Delphi) бағдарламалау тілінде әзірленген алгоритмдерді іске асыратын көрсетілген әдістермен теңдеудің түбірін нақтылау үшін бағдарлама жасау. Бағдарламаның көмегімен теңдеудің кез келген тамырын нақтылаңыз .
4. Есептерді MathCad немесе Excel құралдарымен шешу.
5. Тамырды бөлу және нақтылау кезінде пайдаланылған а параметрі үшін x-тен F(X,a) функциясының кестесін құру.

1.3 Математикалық модель

Инженерлік есептеулерде функция анықталған және үздіксіз болатын кейбір учаскеде сызықты емес теңдеуді шешу қажеттілігі туындайды. Практикада жақын коэффициенттері бар теңдеулер кездеседі және оларды шешу үшін сандық әдістер қолданылады. Бұл әдістер аналитикалық және шебер қолдарға қарағанда әлдеқайда ыңғайлы, аналитикалық әдістер үшін мүлдем қол жетпейтін көптеген теңдеулердің шешімін алуға мүмкіндік береді. Сандық әдістер берілген кесіндіде берілген дәлдікпен теңдеудің тамырын алуға мүмкіндік береді. Сызықты емес теңдеулерді шешу процесі екі кезеңнен тұрады:
1. Түбірлердің бөлінуі, яғни осы теңдеудің тек бір түбірі бар кесінділерді табу. Ол үшін сандық немесе графикалық әдістер қолданылады. Соңғы жағдайда функция графигі құрылады және теңдеулердің тамыры графиктің абсцисс осімен қиылысу нүктелерінде болады. Сандық зерттеуде функция мәндерінің кестесін құрайды. Егер ол белгіні қарама-қарсы өзгертсе, онда бұл учаскеде түбірі бар. Және туынды функцияларды табу және оны монотондылық пен экстремумға тексеру қажет. Функция осы учаскеде жалғыз түбірі бар, егер оның туындысы өз белгісін сақтаса.
2. Бөлінген түбірдің мәнін белгілі бір дәлдікке дейін анықтау.

Хорд әдісі

Жанасу әдісін іске асыра отырып, әрбір Итерация кезінде тек 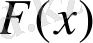функциясының мәнін ғана емес, оның туындысын да есептеу қажет. Алайда, Ньютон әдісінің нұсқасы бар , онда тек 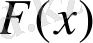мәндерін есептеуді шектеуге болады, бұл кейде есептеу алгоритмін жеңілдетеді.
Егер формулаға қойсаңыз:
,
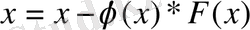
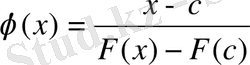ал аралық соңын алу ретінде 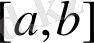, онда ,
онда итерациялық әдіске келеміз:

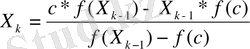
хорд әдісі деп аталады (немесе секущий әдісі).
Бұл жағдайда 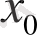ретінде 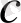(яғни ,онда 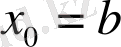немесе керісінше) таңдаудан кейін қалған 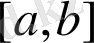аралығының сол ұшын қабылдаған жөн. Бұдан әрі бірізділік формула бойынша құрылады. Тамырға жақындау дәрежесін бағалау теңсіздіктің көмегімен мүмкін:

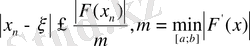
(ол қарастырылатын әдістерге байланысты емес Лагранж формуласының көмегімен алынды).
Әдістің геометриялық мағынасы (оның арқасында ол атау алды) (1.1 сурет). Бұл жағдайда 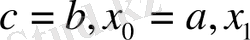қисықтың ұштарын абсцисс осімен қосатын Хорданың қиылысу нүктесіне сәйкес келеді. Одан әрі 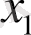абсциссасы бар қисық нүкте орналасқан , келесі хорда және т.б. жүргізіледі [2]. Бұл әдіс шаршы ұқсастыққа ие.
Хорд әдісімен теңдеуді шешу кезеңдері:
1. Жақындауды табу.
2. Берілген дәлдікке қол жеткізуді тексеру.
3. Келесі жақындауды табу.
4. Егер талап етілетін дәлдікке қол жеткізілсе, міндет шешілді.

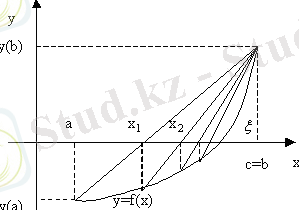
1.1 сурет - Хорд әдісінің геометриялық мағынасы

1.3.2 Кесіндіні екіге бөлу әдісі

Әдістің мәні мынада: бастапқы жақындау ретінде таңдалады
,
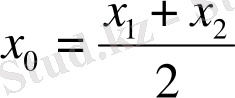мұнда 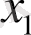, 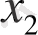-кесіндінің ұштарының координаттары. Содан кейін нүктедегі функция белгілері тексеріледі:

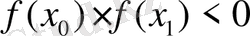
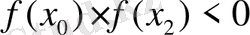
Интервал 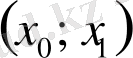(немесе 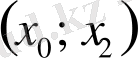) екіге бөлінеді және ұштарында шарт және т. б.орындалатын интервалды таңдайды. егер түбірді 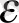дәлдігімен анықтау қажет болса, онда екіге бөлу кесіндінің ұзындығы 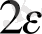-ден кем болмайынша жалғасады. Бұл жағдайда соңғы бөліктің жартысы және қажетті дәлдіктің түбірі бар.
Кесіндіні екіге бөлу әдісі жинақтылықтың сызықтық жылдамдығына ие. Дәлдікке жету үшін N итерацияларды орындау жеткілікті, мұнда

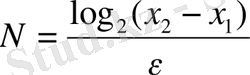
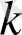-ші және 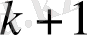-ші итерация қателігі арақатынасымен байланысты:
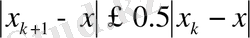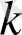, =1,2,3,...
Кесіндіні екіге бөлу әдісінің геометриялық мағынасы (сурет 1.2).

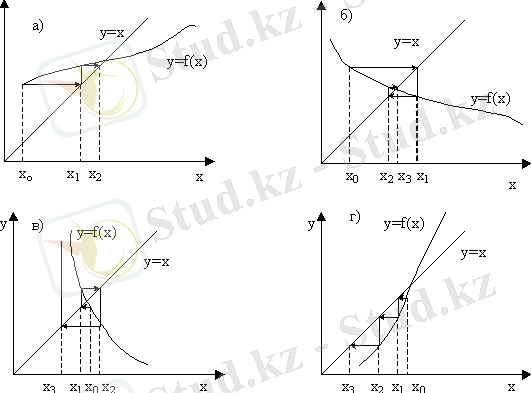
1.2 сурет- Графиктердің әртүрлі нұсқаларында кесіндіні екіге бөлу әдісінің геометриялық мағынасы

1.3.3 Жанама әдіс

Әдістің мәні келесідей [2]:
1. 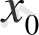түбірінің бастапқы жақындауы таңдалады
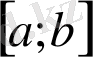
2. 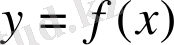графигіне қатысты 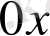осімен қиылысқанға дейін жүргізіледі . Бұл нүкте (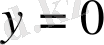) тамырдың келесі жақындауы болатын 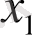дегенді білдіреді:

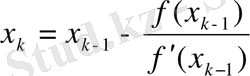
Итерациялық процесс әлі жалғасуда:
,
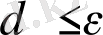
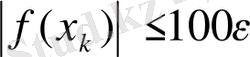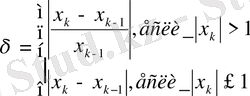, мұнда 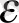-есептеулердің берілген қателігі.
Бастапқы жақындау келесі шартты орындау кезінде таңдалады:

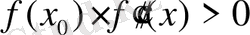
Әдісінің геометриялық мағынасы (сурет 1.3).

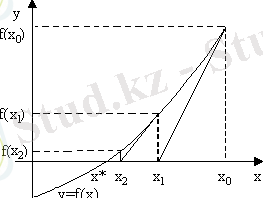
1.3 сурет - Әдісінің геометриялық мағынасы

Егер шарт орындалса, онда әдістің ұқсастығына кепілдік беріледі. Көбінесе бастапқы жақындау ретінде сол кесіндінің ұшының координаты таңдалады. Ньютон әдісінің жинақталу жылдамдығы квадраттық тәуелділікке ие.
Бастапқы жақындауды таңдау қиын болған ерекше жағдайларда, теңдеуді теңдеу бөлікті екіге бөлу әдісімен шешіледі және алынған мән Ньютон әдісі арқылы нақтыланады.

Есепті шешу алгоритмі

1.4.1 Хорд әдісі

1.Бастапқы деректерді енгізу, мұнда a - кесіндінің басы, b - кесіндінің соңы, x0 - бастапқы жақындау және eps - талап етілетін дәлдік.
2.Тексереміз жартысын кесіндінің [a;b], яғни кесінді [a,x0] бар тамыры. Егер шарт орындалса, онда 3-ші блокқа, әйтпесе 4-ші блокқа ауысамыз.
3.Қажетті кесінді [a,x0]. X0 түбірін анықтаңыз және X1 түбірін аламыз. Q параметрін есептейміз (х1 түбіріне дейінгі кезекті жақындау қашықтығын бағалау үшін қолданылады). Х0 мәніне x1 мәнін белгілейміз және нақтыланған түбірді дәлдік шартына сәйкестікке тексереміз. Егер дәлдік шарты х0 - ізделетін шешім орындалса, онда түбірді қайта анықтаймыз..
4.Қажетті кесінді [x0,b]. X0 түбірін анықтаңыз және X1 түбірін аламыз. Q параметрін есептейміз (х1 түбіріне дейінгі кезекті жақындау қашықтығын бағалау үшін қолданылады). Х0 мәніне x1 мәнін белгілейміз және нақтыланған түбірді дәлдік шартына сәйкестікке тексереміз. Егер дәлдік шарты х0 - ізделетін шешім орындалса, онда түбірді қайта анықтаймыз.
5.Алынған түбірді шығарамыз.

Жартылай бөлу әдісі

1. Бастапқы деректерді енгізу, мұнда nn-кесіндінің басы, NK-кесіндінің соңы, x0-бастапқы жақындау және eps-талап етілетін дәлдік.
2. Егер сәйкес келмесе, кесіндінің дәлдігін тексеру шартына сай келетінін тексереміз, онда 3-ші блокқа ауысамыз. Егер кесінді сәйкес келсе, онда функция осы кесіндіде өз белгісін өзгертетінін тексереміз, егер өзгерсе, онда NK айнымалысымен (кесіндінің соңы) x0 (бастапқы жақындау немесе кесіндінің ортасы) мәнін белгілейміз. Егер функция өз белгісін өзгертпесе, онда NN (кесіндінің басы) айнымалысына x0 (бастапқы жақындау немесе кесіндінің ортасы) мәнін береді. Бұл тексерумен біз тамыры жоқ жартысын алып тастаймыз. Ізделіп жатқан кесіндінің жартысын тамырдың бар-жоғына тексергеннен кейін түбірі бар кесінді таңдаймыз және оны екі, кесіндінің ортасын және x0 жаңа бастапқы жақындау бар. Кейін дәлдігін тексеру шартына кері ауысамыз.
3. Алынған бөлікті екіге бөліп, іздеген шешімді аламыз-теңдеудің түбірі.
4. Алынған түбірді шығарамыз.

Жанама әдіс

1.Бастапқы деректерді енгізу, мұнда a-кесіндінің басы, b-кесіндінің соңы, x0-бастапқы жақындау және eps-талап етілетін дәлдік.
2.Егер шарт орындалса, түбірді нақтылауға көшеміз, X1 жаңа түбірін аламыз және оны x0 береміз. Егер түбір дәлдік шартын қанағаттандырса, онда 3-блокқа ауысамыз, егер дәлдік шартын қанағаттандырмаса, қайтадан нақтылаймыз. Егер x0 жинақтылық шартын қанағаттандырмаса, онда бастапқы жақындауға кесіндінің басталу мәнін, яғни а және 3-блокқа ауысамыз.
3. Егер шарт орындалса, онда 2-ші блокқа ұқсас әрекеттерді орындаймыз және 4-ші блокқа ауысамыз. Егер x0 жинақтылық шартын қанағаттандырмаса, онда бастапқы жақындауға кесінді шетінің мәнін, яғни b және 4-блокқа ауысамыз.
4. Егер шарт орындалса, онда 2 блогына ұқсас әрекеттерді орындаймыз және іздеу шешімін аламыз-теңдеудің түбірі.
5. Алынған түбірді шығарамыз.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.