Электрмагниттік өрісте зарядталған бөлшектің қозғалысы


ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Комерциялық емес акционерлік қоғамы
«АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ»
ЭЛЕКТР ЭНЕРГЕТИКА ЖӘНЕ ЭЛЕКТР ТЕХНИКА ИНСТИТУТТЫ
«Техникалық физика кафедрасы»
СТУДЕНТТІҢ ӨЗІНДІК ЖҰМЫСЫ № 1
Пәні: Электрдинамика. Тербелістер мен толқындар.
Мамандығы: 5В071800 - Электрэнергетика.
Тобы: ЭЭк - 17-2.
Нұсқа: № 17.
Орындаған : Сисенбаев Н. М.
Қабылдаған : асс. Азилкияшева М. М.
«» 2018 ж.
(Бағасы) (Қолы)
Алматы, 2018
Тақырып № 1. Электрмагниттік өрісте зарядталған бөлшектің қозғалысы.
Жұмыс мақсаты: Электр және магнит өрістерінде зарядталған бөлшектің динамикасын зерттеу.
1. 1 Тапсырма:
1. 1. 1 Электр өрісіндегі зарядталған бөлшектің қозғалысы.
1. 1. 2 Магнит өрісінде зарядталған бөлшектің қозғалысы.
1. 2 Бақылау сұрақтары
1. 2. 1 Электр өрісіндегі зарядталған бөлшектің қозғалысының дифференциалдық теңдеулері.
1. 2. 2 Қозғалыс теңдеулерінің шешімдері және талдамы.
1. 2. 3 Магнит өрісіндегі зарядталған бөлшектің қозғалысының дифференциалдық теңдеулері.
1. 2. 4 Қозғалыс теңдеулерінің шешімдері және талдамы.
1. 2. 5 Электрмагниттік өрісте зарядталған бөлшектің қозғалысының қолданысы.
1. 1. 1. Электр өрісіндегі зарядталған бөлшектің қозғалысы.
Біз металдардағы, шала өтқізгіштердегі, вакуум мен газдағы электр тогын туғызатын негізгі процесс электр қозғалыстағы электр зарядтары мен электр өрісінің өз ара әсері екенін көрдік. Енді зарядталған бөлшектердің (электронный, ионның) біртекті және өзгермейтін электр өрісіндегі қозғалысын қарастырайық. Егер epic біртекті болмаса және зарядталған бөлшектердің өз ара әсерін еске алсақ, онда мәселе тіпті қиындайды. Реалды приборларда epic әрқашан да біртекті болмайды. Бірақ сол өрістің аса бір азғантай кәлемін бөліп алсақ, оны біртекті деуге болады. Сонымен бірге, көп жағдайда қозғалыстағы зарядталған бөлшектер бір-бірінен соншалықты қашық келеді, сондықтан тіпті олардың зарядтарының өз ара әсерін ескермеуге де болады. Егер зарядталған бөлшектер өрістің бағытымен орын ауыстырса (бөлшектердің жылдамдық векторы

электр өрісінің кернеулігінің векторымен сәйкес келеді), онда оған кернеулік векторының бойымен бағытталған:
F = qE (1. 1)
күш эсер етеді (41-сурет) Кинетикалық энергияныц өзгеруі туралы теорема бойынша бұл күштің жолдағы жұмысы: A=Fl=mv/2-mv/2=qEt=qU
болады. Мұндағы U - өрістің екі нүктесі арасындағы жол участогын шектейтін потенциалдар айырымы. Екіншіден, Ньютонның екінші заңы бойынша F күш бөлшекке
a=F/m (1. 2)
үдеу береді. Демек, зарядталған бөлшектің электр өрісіндегі қозғалысы үдемелі және бөлшектіқ кинетикалық энергиясы барған сайын артады.
Егер бастапқы жылдамдық нольге тең болса, онда кинетикалық энергия формуласы былай болады:
mv/2=qU (1. 3)
Бұл өрнек үдетуші потенциалдар айырымын (U) жүріп өткен бөлшектің ақырғы жылдамдығын анық-тауға мүмкіндік береді. Ол: V=2q/mU (1. 4)
Электрон үшін: q=e.
Электр өрісінің кернеулігі векторының бағытымен оң зарядқа эсер ететін күштің бағыты сәйкес келеді дедік. Ал электрондар теріс зарядты болғандықтан, электр ерісіндегі оған әсер ететін күш өріске қарсы
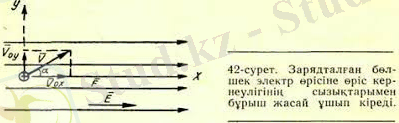
бағытталады, демек, осы параграфтағы оірінші фор-муланың оң жақ бөлігіне «минус» таңбасын қою керек. Енді бөлшектің жылдамдық векторы кернеулік векторына бұрыш жасай бағытталсын делік (42-сурет) . Мұнда жылдамдық векторын суретте көрсетілгендей етіп екі құраушыға жіктейміз. Сонда жылдамдықтың бір құраушысы (1. 5)
өрістің бойымен бағытталады. Бұл бағытта Ғ күштің әсерінен бөлшек үдей қозғалады. Ал енді (1. 6)
құраушы жылдамдығының бойымен белшекке күш әсер етпейді, бұл бағытта бөлшек бір қалыпты және түзу сызықты қозғалады. Механикадан белгілі, бұл қарастырылып отырған жағдайда бөлшек парабола бойымен қозғалады.
Егер тоғы бар өткізгішті біртекті магнит өрісіне орналастырсақ, онда оған
Ғ = ВLІsin (1. 7)
күш әсер етеді. Мұндағы В - өрістің магнит индукциясы;
L - өткізгіштің ұзындығы;
I- өткізгіштегі ток күші;
- токтың бағыты мен магнит индукциясы векторының арасындағы бұрыш.
Заряды q бөлшек өріске v жылдамдықпен ұшып кірді және соншалықты аз t уақыт ішінде S жол жүрді дейік. Зарядтың қозғалысы ұзындығы L өткізгіштегі І - ток сияқты. Сондықтан
F =BL q/t sin = qBL/t sin = qBv sin (1. 8)
Магнит өрісінің зарядталған бөлшекке әсер ететін бұл күшін Лоренц күші деп атайды.
Ол: = qBv sin (1. 9)
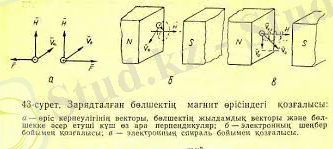
Ең алдымен бөлшектің жылдамдық векторы индукция векторына перпендикуляр жағдайды (sin = 1) қарастырайық. Лоренц күшінің бағытын анықтау үшін сол қол ережесін пайдаланамыз: ол үшін сол қолдың төрт саусағын жаза ұстап, оларды оң зарядталған бөлшектің жылдамдық векторының бағытымен бағыттап, ал магнит индукциясы векторы алақанға енетіндей етіп орналастырсақ, сонда керіп ұстаған бас бармақ бөлшекке әсер ететін күштің бағытын көрсетеді. Егер зарядталған бөлшек электрон болса, онда қолдың төрт саусағын бөлшек жылдамдығының векторына қарсы бағыттау керек, өйткені токтың бағыты электрондардың орын ауыстыру бағытына қарсы болады.
Бұл айтылғандар күштің өpic индукциясының векторына да, сондай-ақ жылдамдық векторына да перпендикуляр екендігін көрсетеді (43 а-сурет) . Ал егер күш жылдамдық векторына перпендикуляр болса, онда жұмыс нольге тең де, кинетикалык энергия өзгермейді, демек, жылдамдық нольге тең. Сонымен бірге, егер денеге жылдамдық векторына перпендикуляр бір, тек бір ғана күш әсер етсе, онда ол центрге тартқыш күш болатыны бізге механикадан белгілі. Ол мынаған тең:
F=mv/R (1. 10)
1. 1. 2 Магнит өрісінде зарядталған бөлшектің қозғалысы.
Магнит өрісі. Электр зарядтары қоршаған ортада электр өрісі пайда болатыны сияқты токтар мен тұрақты магниттермен қоршаған ортада күш өрісі - магнит өрісі пайда болады.
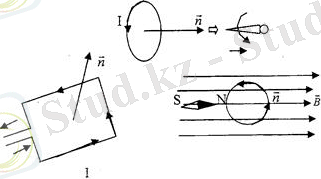 Айналдырушы күш моменті.
Айналдырушы күш моменті.
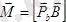 . Бұл
. Бұл
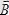 магнит индукциясы векторы магнит өрісінің сандық мәнін көрсетеді,
магнит индукциясы векторы магнит өрісінің сандық мәнін көрсетеді,
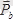 - тоғы бар рамканың магнит моменті.
- тоғы бар рамканың магнит моменті.
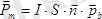 бағыты оң нормальдың бағытымен сәйкес келеді. Сонымен
бағыты оң нормальдың бағытымен сәйкес келеді. Сонымен
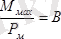 (2. 1)
(2. 1)
1-сурет - магнит өрісінің сипаттамасы және магнит индукция векторы.
Француз оқымыстылары Ж. Био, Ф. Савар тұрақты ток магнит өрістерін зерттей алған ғылыми нәтижелерін математика тұрғысынан тұжырымдап заң түріне келтірген француз математигі мен физигі Лаплас болды.
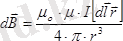 (2. 2)
(2. 2)
Мұнда
r
-
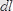 -бөлігінен өрістің А нүктесіне жүргізілген радиус-вектор.
-бөлігінен өрістің А нүктесіне жүргізілген радиус-вектор.
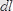 - өткізгіштің кішкене бөлігі.
- өткізгіштің кішкене бөлігі.
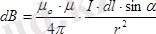 (2. 3)
(2. 3)
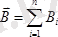 (2. 4)
(2. 4)
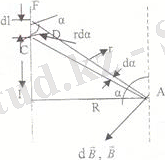
2-сурет 3-сурет
Түзу токтың магнит өрісі. Ұзындығы шексіз жіңішке түзу өткізгіштен ток өтіп жатсын (3-сурет) .
Өткізгіш өсінен
R
қашықтықтағы
А
нүктесіндегі
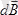 токтың барлық бөліктерінен бағыты бірдей болады және чертеждың жазықтығына перпендикуляр болып (бізге қарап) бағытталады.
токтың барлық бөліктерінен бағыты бірдей болады және чертеждың жазықтығына перпендикуляр болып (бізге қарап) бағытталады.
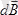 қосуды осы себептен олардың модульдерін қосумен алмастыруға болады.
қосуды осы себептен олардың модульдерін қосумен алмастыруға болады.
 -бұрышы -
-бұрышы -
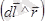
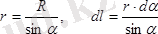 ,
,
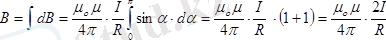
екенін аламыз. (3-сурет) .
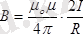 (2. 5)
(2. 5)
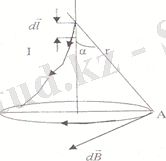
Тогы бар дөңгелек өткізгіштің центріндегі магнит өрісі(4-сурет) .
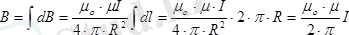
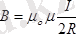 (2. 6)
(2. 6)
Лоренц күші. Магнит өрісіндегі зарядталған бөлшектердің қозғалысы.
Тәжірибеден магнит өрісі қозғалыстағы жеке зарядтарға да әсер етеді екен. Магнит өрісінде
 жылдамдықпен қозғалып келе жатқан
q
электр зарядына әсер ететін күш Лоренц формуласымен беріледі.
жылдамдықпен қозғалып келе жатқан
q
электр зарядына әсер ететін күш Лоренц формуласымен беріледі.
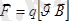

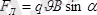 (2. 7)
(2. 7)
Лоренц күшінің бағыты сол қол ережесімен анықталынады.
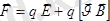
Лоренц күшінің бағыты және осы күштің арқасында зарядталған бөлшектердің магнит өрісіндегі ауытқу бағыты бөлшектердің q зарядының таңбасына тәуелді болады.
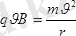 ,
,

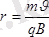 (2. 8)
(2. 8)
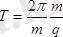 (2. 9)
(2. 9)
Ампер күші.
Магнит өрісінің тоғы бар әр түрлі өткізгіштерге әсерін зерттей отырып, Ампер: бойында тоғы бар ұзындығы
 өткізгіш элементіне магнит өрісінде әсер ететін күш ток күші I-ге, өткізгіштің ұзындығы
өткізгіш элементіне магнит өрісінде әсер ететін күш ток күші I-ге, өткізгіштің ұзындығы
 элементінің магнит индукциясы
элементінің магнит индукциясы
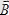 көбейтіндісіне тура пропорционал екендігін тапты (5-сурет) .
көбейтіндісіне тура пропорционал екендігін тапты (5-сурет) .
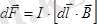 (2. 10)
(2. 10)
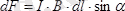 (2. 11)
(2. 11)
- Ампер күшінің өрнегі.
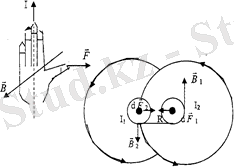
5 - сурет

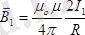
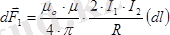 (2. 12)
(2. 12)
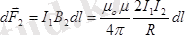 (2. 13)
(2. 13)
Магнит өріс үшін Гаусс теоремасы.
Магнит индукциясы векторының
dS
ауданы арқылы өтетін ағыны
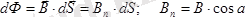
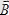 - векторының
dS
ауданына перпендикуляр бағытқа проекциясы.
- векторының
dS
ауданына перпендикуляр бағытқа проекциясы.
 -векторының ағыны cosα-ның мәніне байланысты оң да, теріс те болуы мүмкін.
-векторының ағыны cosα-ның мәніне байланысты оң да, теріс те болуы мүмкін.
 - нормалының оң бағыты ток пен оң бұранда ережесі арқылы байланысады (6-сурет) .
- нормалының оң бағыты ток пен оң бұранда ережесі арқылы байланысады (6-сурет) .
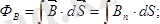 (2. 14)
(2. 14)
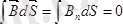
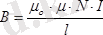 ,
,
бұдан
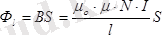 .
.
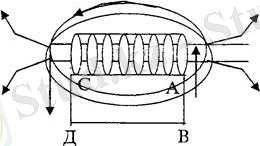
Соленоидтың барлық орамдарымен жалғасқан толық магнит ағыны тіркелген ағын деп аталынады.
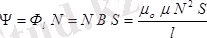 (2. 15)
(2. 15)
Главная Категории Заказать
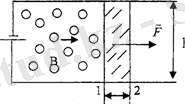
Тогы бар өткізгішті магнит өрісінде орын ауыстыру кезіндегі істелетін жұмыс.
Магнит өрісіндегі өткізгішке Ампер заңымен анықталатын күштер әсер етеді. Егер өткізгіш бекітілмесе, онда Ампер күшінің арқасында өткізгіш орын ауыстырады. Сонымен тоғы бар өткізгішті орын ауыстыру кезінде магнит өрісі жұмыс жасайды (7-сурет) . Ампер заңы бойынша
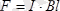 ,
,
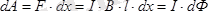 .
.
Сонымен
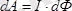 (2. 16)
(2. 16)
яғни магнит өрісінде тогы бар өткізгішті орын ауыстырған кезде жасалынатын жұмыс ток күшін өткізгіш қозғалған кезде қиып өткен магнит ағынының көбейтіндісіне тең шама.
Магнетиктер. Магниттік гестерезис. Кюри температурасы.
Өткізгіштерде өтетін токтардың магнит өрісіндегі кез келген магнетик ерекше күйге келеді - осыны магниттелу деп атайды. Сөйтіп, магнетик магниттелген кезде ондағы микротоктардың магнит өрістерін не күшейтеді, не қарсы әсер етіп әлсіретеді.
Сонымен жалпы кез келген ортадағы магнит индукциясының векторы дегеніміз макроскопиялық (
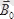 ) және микроскопиялық (
) және микроскопиялық (
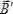 ) токтар туғызатын индукциялық векторларының қосындысы болып табылады:
) токтар туғызатын индукциялық векторларының қосындысы болып табылады:
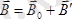 (2. 17)
(2. 17)
1) Егер
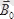 және
және
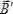 векторлары бағыттас болса, онда олар қосылып
векторлары бағыттас болса, онда олар қосылып
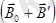 , жалпы ортадағы магнит өрісін күшейтеді де ортаның магнит өтімділігі
, жалпы ортадағы магнит өрісін күшейтеді де ортаның магнит өтімділігі
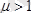 болады. Мұндай қасиеті бар заттарды парамагнетиктер деп атайды.
болады. Мұндай қасиеті бар заттарды парамагнетиктер деп атайды.
2) Егер
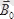 және
және
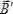 векторлары бір-біріне қарама-қарсы бағытталса, онда жалпы ортадағы магнит өрісі әлсірейді де ортаның магнит өтімділігі кемиді,
векторлары бір-біріне қарама-қарсы бағытталса, онда жалпы ортадағы магнит өрісі әлсірейді де ортаның магнит өтімділігі кемиді,
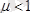 болады. Мұндай қасиеті бар заттар диамагнетиктер деп аталады.
болады. Мұндай қасиеті бар заттар диамагнетиктер деп аталады.
3) Егер
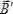 >
>
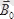 болса, осындай қасиеті бар заттар ферромагнетиктер деп аталады. Олар үшін
болса, осындай қасиеті бар заттар ферромагнетиктер деп аталады. Олар үшін
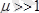 болады.
болады.
Парамагнеттік заттарға O 2 , NO 3 , Al, Pt, сирек кездесетін элементтер, сілтілер және т. б. заттар жатады. Диамагнетик заттарға инертті газдар, көптеген органикалық қоспалар, шайыр, су, шыны, мәрмәр, т. б. жатады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz