Эконометрика пәні: модельдер мен ықтималдық-статистикалық негіздер


Қазақстан Республикасының Білім және ғылым министрлігі
Әл-Фараби атындағы Қазақ Ұлттық университеті
Экономика және бизнес жоғарғы мектебі
Бизнес-технология кафедрасы
Логистика мамандығы

СӨЖ
Тақырыбы: «Эконометрика пәні»
Орындаған: Садуақас Д. А
Тексерген: Тұраров Д. Р.
Алматы қаласы
2019-2020 оқу жылы
Жоспар
- Эконометрика пәні және оның міндеттері
- Модельдер
- Оқиғалар, оқиғаның ықтималдылығы
- Кездейсоқ шама
- Кездейсоқ шамалардың сандық сипаттамалары
- Кездейсоқ шамалардың үлестіру заңдары
- Кездейсоқ шамалардың өзара байланысы
- Жоғардағы аталған сұрақтарға мысал ретінде есептерді ашып көрсет
- Пайдаланылған әдебиеттер
1. Эконометрика пәні
Эконометрика - бұл теорияларды құру немесе экономикадағы бар гипотезаларды тексеру және тарихи деректерден болашақ тенденцияларды болжау үшін деректерді қолданатын статистикалық және математикалық модельдерді сандық қолдану. Ол нақты деректерді статистикалық сынақтарға өткізеді, содан кейін нәтижелерді теорияға немесе сыналған теорияларға қарсы салыстырады
Сіз қолданыстағы теорияны сынап көруге немесе осы бақылауларға негізделген жаңа гипотезаны жасау үшін бар деректерді пайдалануға қызығушылық танытатындығыңызға байланысты эконометрика екі негізгі категорияға бөлінуі мүмкін: теориялық және қолданбалы.
Эконометрика негіздері. Эконометрика мәліметтерді статистикалық әдістерді қолдана отырып, экономикалық теорияны тексеру немесе дамыту мақсатында талдайды. Бұл әдістер жиілікті бөлу, ықтималдық пен ықтималдылықты бөлу, статистикалық анықтама, корреляциялық талдау, қарапайым және көп регрессиялық талдау, бір мезгілде теңдеулер модельдері және уақыт қатарлары сияқты құралдарды пайдалану арқылы экономикалық теорияларды сандық бағалауға және талдауға арналған статистикалық тұжырымдарға сүйенеді.
Эконометриканы Лоуренс Клейн, Рагнар Фриш және Саймон Кузнец бастаған. Үшеуі де өз үлестері үшін 1971 жылы экономика бойынша Нобель сыйлығын алды. Бүгінгі күні ол академиктермен қатар Уолл-стрит трейдерлері мен талдаушылары сияқты практиктердің арасында үнемі қолданылады.
Эконометриканы қолданудың мысалы - бақыланатын деректерді қолдана отырып, кірістердің әсерін зерттеу. Адам өзінің табысын көбейткен сайын оның шығыны да артады деп болжауы мүмкін экономист. Егер деректер осындай бірлестіктің бар екендігін көрсетсе, онда кіріс пен тұтыну арасындағы байланыстың беріктігін және оның қатынасы статистикалық маңызды ма, жоқ па, соны түсіну үшін регрессиялық талдау жүргізілуі мүмкін, яғни оның болуы екіталай болып көрінеді.
Эконометрика әдістемесі. Эконометрикалық әдіснамадағы алғашқы қадам - мәліметтер жиынтығын алу және талдау және жиынтықтың сипаты мен формасын түсіндіретін нақты гипотезаны анықтау. Бұл мәліметтер, мысалы, қор индекстің тарихи бағалары, тұтынушы қаржысын зерттеу кезінде алынған бақылаулар немесе әр түрлі елдердегі жұмыссыздық пен инфляция деңгейлері болуы мүмкін. Егер S&P 500 бағасының жыл сайынғы өзгеруі мен жұмыссыздық деңгейінің арасындағы байланыс сізді қызықтырса, сіз екі мәліметтер жиынтығын жинайсыз. Бұл жерде сіз жұмыссыздықтың жоғарылауы қор нарығындағы бағаның төмендеуіне әкеледі деген ойды сынап көргіңіз келеді. Осылайша, қор нарығының бағасы сіздің тәуелді ауыспалы, ал жұмыссыздық деңгейі тәуелсіз немесе түсіндірілетін өзгермелі болып табылады.
Ең көп таралған қатынас сызықтық болып табылады, яғни түсіндірме айнымалыдағы кез-келген өзгеріс тәуелді айнымалымен оң корреляцияны білдіреді, бұл жағдайда қарапайым регрессиялық модель көбінесе осы қатынасты зерттеу үшін қолданылады, бұл олардың арасында ең жақсы сызықты құруға мүмкіндік береді. екі деректер жиынтығы, содан кейін әр нүктенің орташа алғанда сол жолдан қаншалықты алыстығын тексеру үшін тестілеу.
Талдауда бірнеше түсіндірме айнымалылар болуы мүмкін екенін ескеріңіз - мысалы, ЖІӨ-нің өзгеруі және инфляция қор нарығындағы бағаны түсіндіруде жұмыссыздықпен қатар. Бірнеше түсіндірме айнымалыны қолданған кезде оны бірнеше сызықты регрессия деп атайды, яғни эконометрикада жиі қолданылатын құрал.
Регрессияның әртүрлі модельдері. Бірнеше әртүрлі регрессиялық модельдер бар, олар талданатын деректердің сипатына және сұрақтың түріне байланысты оңтайландырылады. Ең көп таралған мысал - қарапайым квадраттардың (OLS) регрессиясы, оны бірнеше қима немесе уақыт қатарлары бойынша жүргізуге болады. Егер сізді екілік нәтиже (иә-жоқ) нәтижесі қызықтырса - мысалы, жұмыста жұмыстан шығарылу мүмкіндігіңіз (иә, сіз жұмыстан босатылдыңыз, немесе жоқ, сіз істей алмайсыз) - сіздің өнімділігіңізге байланысты логистикалық регрессия немесе пробит моделі. Бүгінгі таңда эконометрологтың қолында жүздеген модельдер бар. Енді эконометрика STATA, SPSS немесе R сияқты осы мақсаттарға арналған статистикалық талдаудың бағдарламалық пакеттерін қолдана отырып жүргізілуде. Бұл бағдарламалық пакеттер сонымен қатар осы модельдер шығарған эмпирикалық нәтижелер жай нәтиже емес екендігіне қолдау көрсету үшін статистикалық маңыздылығын оңай тексере алады. мүмкіндік. R-квадраты, t-тестілер, p-мәндер және нөл-гипотезаларды тестілеу - эконометриктер модель нәтижелерінің дұрыстығын бағалау үшін қолданатын әдіс.
Эконометрика - статистика мен математикалық модельдердің сандық түрде қолданылуы, теорияны құру немесе экономикадағы бар гипотезаларды тексеру үшін.
Эконометрика регрессиялық модельдер және нөлдік гипотезаны тексеру сияқты әдістерге сүйенеді.
Эконометрика болашақ экономикалық немесе қаржылық тенденцияларды болжауға тырысу үшін де қолданыла алады. [2]
2. Модельдер
Эконометрикалық модельдер экономикалық деректер негізінде статистикалық анықтама әдістерінің көмегімен жасалады. Бұл модельдер әдетте экономикалық агенттердің іс-әрекетін оңтайландыруды болжайтын экономикалық теорияларға негізделген.
Эконометриялық модельдерді құруда пайдаланылатын негізгі мәліметтер баға мен мөлшер туралы бақылаулар болып табылады. Бұл деректер уақыт қатарлары немесе көлденең қималар немесе екеуінің жиынтығы (панельдік мәліметтер) болуы мүмкін. Деректер қандай да бір жинақтау деңгейіндегі фирмалардың немесе үй шаруашылықтарының нақты сатып алуларын көрсетеді. Тұтынушылар әртүрлі мөлшердегі тауарларды (тікелей тұтынуға арналған тауарлар немесе басқа тауарларды өндіруде қолданылатын тауарлар) салыстырмалы бағалар мен кірістердің немесе шығарылымдардың әртүрлі жиынтығынан алады.
Деректер бойынша есептелген теңдеулер, әдетте, оңтайландыру мәселесінен туындайтын бірінші кезектегі шарттардан алынады (мысалы, пайдалылық немесе кірісті көбейту) . Мінез-құлық (тауарларды сатып алу) туралы мәліметтер осылайша технологияның немесе талғамның негізгі құрылымын анықтау үшін қолданылады. Негізгі құрылым белгілі болғаннан кейін, үлгіні салыстырмалы бағалар мен кірістер мен шығыстардың кез-келген жиынтығында тұтынылатын белгілі бір тауардың мөлшерін болжау үшін қолдануға болады. Басқаша айтқанда, бүкіл кесте агент мінез-құлқын бақылаудың нақты жиынтығынан алынған. Эконометрикалық модельдер эконометрикада қолданылатын статистикалық модельдер. Эконометрикалық модель белгілі бір экономикалық құбылысқа қатысты әртүрлі экономикалық шамалар арасында болатын статистикалық қатынасты анықтайды. Эконометрикалық модель детерминистік экономикалық модельден, белгісіздікке жол беру арқылы немесе өзі стохастикалық болып табылатын экономикалық модельден алынады. Алайда, қандай-да бір нақты экономикалық теорияға байланбаған эконометриялық модельдерді де қолдануға болады. [3] Эконометрикалық модельдің қарапайым мысалы - тұтынушылардың ай сайынғы шығындары алдыңғы айдағы тұтынушылардың кірістеріне байланысты болады. Сонда модель теңдеуден:
Ct=a+bYt-1+et
{\displaystyle C_{t}=a+bY_{t-1}+e_{t}, }тұрады
мұндағы C - тұтынушының t айындағы шығындары, Yt-1 - өткен айдағы табыс, және де модель тұтынуды толық түсіндіре алмайтын қателіктер термині. Содан кейін эконометрологтың міндеті - a және b параметрлерінің бағаларын алу; Модельдің теңдеуінде пайдаланылған параметрлердің есептік мәндері болашақ тұтынудың алдыңғы айдағы кірісіне байланысты болжау жасауға мүмкіндік береді.
Жалпы эконометрикалық модельдердің кейбірі:
- Сызықтық регрессия
- Жалпыланған сызықтық модельдер
- Ықтимал
- Логит
- Тобит
- ARIMA
- Векторлық авторегрессия
- Квинтеграция
- Қауіп
Эконометрикада, жалпы статистика сияқты, талданатын шамаларды кездейсоқ шамалар ретінде қарастыруға болады. Осыдан кейін эконометрикалық модель дегеніміз зерттелетін айнымалылардың бірлескен ықтималдылықтың нақты үлестірілуі тиесілі болатын бірлескен ықтималдылықты бөлудің жиынтығы. Осы жиынның элементтерін нақты бағаланатын параметрлердің шексіз саны бойынша индекстеуге болатын жағдайда модель параметрлік модель деп аталады; әйтпесе бұл параметрлік емес немесе жартылайараметикалық модель. Эконометриканың көп бөлігі модельдерді таңдау, бағалау және оларға қорытынды жасау әдістерін зерттеу болып табылады. Ең көп таралған эконометрикалық модельдер құрылымдық болып табылады, себебі олар себептік және контрафактивті ақпараттарды жеткізеді, және саясатты бағалау үшін қолданылады. Мысалы, кірістерге негізделген тұтыну шығыстарын модельдеу әдісін тұтынудың кез-келген гипотетикалық деңгейге қандай болатынына байланысты болатынын көруге болады, олардың тек біреуі ғана (салық саясатын таңдауға байланысты) іс жүзінде пайда болады.
3. Оқиғалар. Оқиғаның ықтималдығы
Ықтималдықтар теориясында оқиға - бұл эксперимент нәтижелерінің жиынтығы (үлгілік кеңістіктің жиынтығы), оған ықтималдық тағайындалады. [1] Бір нәтиже көптеген әртүрлі оқиғалардың элементі болуы мүмкін, [2] және эксперименттегі әртүрлі оқиғалар, әдетте, бірдей мүмкін емес, өйткені олар нәтижелердің әртүрлі топтарын қамтуы мүмкін. [3] Оқиға қосымша оқиғаны анықтайды, атап айтқанда толықтырушы жиынтығы (оқиға орын алмаған), және олар бірге Бернулли сотын анықтайды: оқиға болды ма, жоқ па? Әдетте, үлгі кеңістігі шексіз болған кезде, үлгінің кеңістігінің кез-келген жиынтығы оқиға болып табылады (яғни, үлгі кеңістігінің қуат жиынтығының барлық элементтері оқиғалар ретінде анықталады) . Алайда, бұл әдіс таңдау кеңістігі сансыз шексіз болған жағдайда жақсы нәтиже бермейді. Сонымен, ықтималдық кеңістігін анықтаған кезде белгілі бір кеңістіктің кейбір жиынтықтарын оқиғалар болдырмауға болады және қажет болады. Оқиғаның болуы. Кез-келген экспериментте немесе сынақта кез-келген оқиға болуы немесе болмауы ықтималдығы бар. Оқиғаның пайда болу ықтималдығы 0 мен 1 аралығында. S үлгісі кеңістігінің Е оқиғасы деп алсақ, егер эксперименттің нәтижесі ω болса, occurred ∈ болса, пайда болды деп айтылады, алайда егер нәтиже ω болса, онда the ∉ E оқиға болған жоқ деп айтамыз. Карточкаларды ойнаудың мысалын келтірейік. Мұнда Е оқиғасы бет карточкасын салуда. Егер сіз күрек патшасын тартсаңыз, онда Е оқиғасы болды дейміз. Алайда, сіз сегіз клубты тартсаңыз, біз E оқиғасы болған жоқ дейміз. Оқиғалардың түрлері:
- Қарапайым оқиға. Егер E оқиғасында үлгі кеңістігінің бір ғана нүктесі болса, оны қарапайым оқиға немесе Элемент оқиғасы деп атайды. Бұл дәл бір нәтижеден тұратын оқиға. Мұны мысалмен түсінейік. Сіз өлі лақтырып тастаңыз деп айтыңыз, өлімге 2 пайда болу мүмкіндігі қарапайым оқиға және E = {2} береді
- Құрама оқиға. Қарапайым оқиғадан айырмашылығы, егер үлгі кеңістігінде бірнеше нүкте болса, мұндай оқиға құрама оқиға деп аталады. Бұл екі немесе одан да көп оқиғаны бірге біріктіруді және оқиғалардың осындай комбинациясының ықтималдығын табуды қамтиды. Мәселен, тағы бір мысалды алайық. Егер біз кубикті лақтырсақ, жұп санның пайда болуы мүмкін күрделі оқиға, өйткені бірнеше мүмкіндіктің үш мүмкіндігі бар, мысалы: E = {2, 4, 6}
- Белгілі бір оқиға. Атауы көрсеткендей, кез-келген экспериментте болатын оқиға белгілі бір оқиға. Оқиғаның бұл түрінің ықтималдығы 1-ге тең
- Мүмкін емес оқиға. Екінші жағынан, егер оқиға болмай қалса, яғни оның болмауы мүмкін оқиға деп айтуға болады. Бұл оқиғаның ықтималдығы 0-ге тең. Сіз палубадан шығарған картаңыздың қызыл және қара сияқты болуы да мүмкін емес оқиға.
- Оқиғалар бірдей болуы мүмкін. Егер эксперимент нәтижелері бірдей болатын болса, онда олар бірдей ықтимал оқиғалар деп аталады. Монетаны лақтыру кезінде бастар немесе құйрықтар алу мүмкіндігі бірдей.
- Қосымша оқиғалар. E оқиғасы үшін оқиғаның болмауы оның ақысыз оқиғасы деп аталады. Негізінен ақысыз іс-шаралар - бұл бір уақытта бола алмайтын оқиғалар. Сондықтан өлгенде тақ бет пен тегіс бет алу бір-бірін толықтырады.
- Өзара эксклюзивті оқиғалар. Екі оқиға бір-біріне сәйкес келмейтін екі ерекше оқиға деп айтылады. Өзара эксклюзивті оқиғалар әрқашан әртүрлі нәтижеге ие болады. Екі қарапайым оқиға әрқашан бір-бірінен ерекшеленеді, ал екі күрделі оқиға болуы мүмкін немесе болмауы да мүмкін.
Егер А және В екі оқиға болса, онда
( A ∩ B ) = Ø
P ( A ∩ B ) = 0
P ( A ∪ B) = P (A) + P ( B ) [5]
4. Кездейсоқ шама
Кездейсоқ шама, әдетте жазылғанда X деп белгіленеді, мүмкін мәндері кездейсоқ құбылыстың сандық нәтижелері болатын айнымалы. Кездейсоқ шамалардың екі түрі бар: дискретті және үздіксіз.
Дискретті кездейсоқ шамалар.
Дискретті кездейсоқ айнымалы - бұл 0, 1, 2, 3, 4, . . . сияқты белгілі бір мәндердің сандық санына ғана ие болатын кездейсоқ шамалар, әдетте (бірақ міндетті емес) есептеледі. Егер кездейсоқ айнымалы белгілі бір мәндердің шектеулі санын ғана алса, онда ол дискретті болуы керек. Дискретті кездейсоқ шамаларға мысал ретінде отбасындағы балалар саны, жұмаға түнгі кинотеатрға бару, дәрігердің хирургиясындағы пациенттер саны, он қораптағы жарық шамдарының саны жатады. Дискретті кездейсоқ шаманың ықтималдық таралуы - оның мүмкін болатын мәндерінің әрқайсысымен байланысты ықтималдықтар тізімі. Оны кейде ықтималдық функциясы немесе ықтималдықтың масса функциясы деп те атайды. Кездейсоқ айнымалы X әр түрлі мәндерді алуы мүмкін делік, X = xi P (X = xi) = pi деп анықталды. Пи ықтималдығы келесі талаптарды қанағаттандыруы керек:
1: 0 < p i < 1 әрбәр i үшін
2: p 1 + p 2 + . . . + p k = 1.
Мысалы,
X айнымалы мәні 1, 2, 3 немесе 4 мәндерін қабылдай алады делік. Әр нәтижеге байланысты ықтималдықтар келесі кестеде сипатталған:
Х-тің 2 немесе 3-ке тең ықтималдығы екі ықтималдықтың қосындысы:
P (X = 2 немесе X = 3) = P (X = 2) + P (X = 3) = 0. 3 + 0. 4 = 0. 7. Сол сияқты Х-тің 1-ден үлкен болу ықтималдығы комплемент ережесі бойынша
1 - Р (Х = 1) = 1 - 0, 1 = 0, 9 тең.
Бұл үлестіруді төменде көрсетілген ықтималдық гистограммасы арқылы да сипаттауға болады:

Үздіксіз кездейсоқ шамалар.
Үздіксіз кездейсоқ шама мүмкін мәндердің шексіз санын алатын шама. Үздіксіз кездейсоқ шамалар әдетте өлшеулер болып табылады. Мысалдарға биіктігі, салмағы, апельсиндегі қант мөлшері, бір миль жүгіру үшін қажет уақыт кіреді.
Үздіксіз кездейсоқ шамалар нақты мәндер бойынша анықталмайды. Оның орнына, ол шамалардың интервалында анықталады және қисық сызықты аймақпен ұсынылады (дамыған математикада бұл интеграл деп аталады) . Кез-келген жалғыз мәнді көру ықтималдығы 0-ге тең, өйткені кездейсоқ шамамен қабылдануы мүмкін шамалар саны шексіз.
Кездейсоқ айнымалы X барлық сандарды нақты сандар интервалынан алуы мүмкін делік. Сонда X нәтижесінің A, P (A) жиынтығында болуы ықтималдығы А-дан жоғары және қисық астындағы аудан ретінде анықталады. P (x) функциясын білдіретін қисық келесілерді қанағаттандыруы керек:
1: қисықтың теріс мәндері жоқ (p(x) > 0 барлық x үшін)
2: Қисық астындағы жалпы аудан 1-ге тең. [6]
5. Кездейсоқ шамалардың сандық сипаттамалары
Үлестіру заңы кездейсоқ шаманы сипаттайтынын көрдік. Көптеген практикалық мәселелерді шешкенде кездейсоқ шаманың үлестіру заңын іздестірмей-ақ, сол үлестірудің маңызды ерекшелігін қамтитын кейбір сандық сипаттамаларымен қанағаттануға болады.
Ықтималдықтар теориясында бұл сандық сипаттамалар мен оларға қолданылатын амалдардың ролі өте-мөте зор. Осы сандық сипаттамаларды білу нәтижесінде көптеген ықтималдықтар есептерін шешу жеңілденеді. Әрине, мұндай сандық сипаттамалар көп-ақ. Біз солардың ішінен математикалық күтім, дисперсия, орташа квадраттық ауытқу және реттік моменттерді қарастырамыз.
Сандық сипаттамалрының маңыздыларының біріне математикалық күтім M(X), дисперсия D(X) және орта квадраттық ауытқу(δ) жатады.
Дискретті кездейсоқ шаманың мүмкін болатын мәндерінің сәйкес ықтималдықтарына көбейтінділерінің қосындысын оның
математикалық күтімі
деп атайды.
M(X) белгіленеді:
M(X) =x
1
p
1
+x
2
p
2
+…+x
n
p
n
=
Математикалық күтімнің қасиеттері:
1) Тұрақты шаманың математикалық күтімі тұрақты шаманың өзіне тең:
M(C) =C;
2) Тұрақты көбейткішті математикалық күтім белгісінің сыртына шығаруға болады:
M(CX) =CM(X) ;
3) Тәуелсіз кездейсоқ шамалардың ақырлы санының көбейтіндісінің математикалық күтімі олардың математикалық күтімдерінің көбейтіндісіне тең:
M(X·Y·Z) =M(X) ·M(Y) ·M(Z) ;
4) Кездейсоқ шамалардың ақырлы санының қосындысының математикалық күтімі олардың математикалық күтімдерінің қосындысына тең:
M(X+Y+Z) =M(X) +M(Y) +M(Z) ;
Егер Х кездейсоқ шамасының барлық мәндерін бірдей С санына кемітсе (арттырса) , онда оның математикалық күтімі де сол С санына кемиді (артады) :
M(C-X) =M(X) -C
Х-дискретті кездейсоқ шамасының дисперсиясы (шашырау) дегеніміз, Х пен математикалық күтімінің квадратының математикалық күтімнен ауытқуын атайды:
D(X) =M[X-M(X) ] 2
Дисперсияны есептеу үшін келесі формуланы қолданған қолайлы:
D(X) =M(X
2
) -[M(X) ]
2
Дисперсияның қасиеттері:
Тұрақты шама С-ның дисперсиясы 0-ге тең:
D(C) =0;
Тұрақты көбейткішті дисперсия таңбасының алдына квадрат дәрежесін шығаруға болады.
D(CX) =C
2
D(X) ;
Бірнеше өзара тәуелсіз кездейсоқ шамалардың қосындысының дисперсиясы осы шамалардың дисперсияларының қосындысына тең:
D(X+Y+Z) =D(X) +D(Y) +D(Z) ;
Екі тәуелсіз кездейсоқ шамалардың айырмасының дисперсиясы осы шамалардың дисперсияларының қосындысына тең:
D(X-Y) =D(X) +D(Y) ;
Х кездейсоқ шамасының орта квадраттық ауытқуы деп дисперсиядан алынған квадрат түбірді атайды:

Дисперсияның өлшемі кездейсоқ шаманың квадратының өлшеміне тең. Себебі, орта квадраттық ауытқуы дисперсиядан алынған квадрат түбірге тең болғандықтан, онда σ(Х) өлшемі Х-тің өлшеміне тең. Сондықтан шашырау бағасы дұрыс болуы үшін орта квадраттық ауытқуды есептейді.
6. Кездейсоқ шамалардың үлестіру заңы
Егер тәжірибе нәтижесінде белгілі бір ықтималдығы бар жарамды мәндерді қабылдай алатын болса, айнымалы кездейсоқ деп аталады. Кездейсоқ шаманың толық, толық сипаттамасы - тарату заңы. Таралу заңы - кездейсоқ шаманың X белгілі бір мәнін қабылдайтын немесе белгілі бір уақыт аралығында болатын ықтималдығын анықтауға мүмкіндік беретін функция (кесте, график немесе формула бойынша берілген) . Егер кездейсоқ шамалар үлестірім заңын берген болса, оның осы заң бойынша таратылатындығын немесе бөлу заңына бағынатындығын айтады.
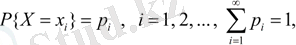
ол айнымалы Х мәніне сәйкес келеді, ол осы мәнді қабылдайды.
Кездейсоқ X өзгермелі деп аталады, егер кез келген a <b үшін теріс емес
f (x) функциясы болса, онда
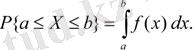
F (x) функциясы үздіксіз кездейсоқ шаманың тығыздық функциясы деп аталады. Кездейсоқ шаманың (дискретті немесе үздіксіз) кездейсоқ шаманың ықтималдығы, кіші х, X кездейсоқ шаманың үлестіру функциясы деп аталады және F (x) деп белгіленеді:
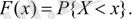
Тарату функциясы кез-келген кездейсоқ шамаларға сәйкес келетін үлестірім заңының әмбебап түрі.
Қалыпты үлестіру
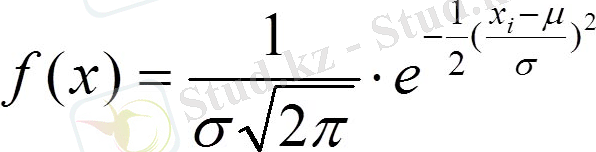
Формуладан қалыпты үлестіру параметрлерімен анықталады, сонымен қатар олар тәуелді:
D(X) =
℮=2. 71828…
үлестіру
Хи-квадрат кездейсоқ шаманың еркіндік дәрежесі n=V-m санымен анықталады. Олай болса
Математикалық үміт және дисперсия:
M( ) =n=V-m D( ) =2n=2(V-m)
Стьюдент үлестіруі.
Математикалық үміті мен дисперсиясы:
M(X) =0 D(T) =
Фишер үлестіруі.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz