Бас жиынтық пен таңдама: вариациялық қатарлар, бағалау әдістері және статистикалық гипотезаларды тексеру


Қазақстан Республикасының Білім және ғылым министрлігі
Әл-Фараби атындағы Қазақ Ұлттық университеті
Экономика және бизнес жоғарғы мектебі
Бизнес-технология кафедрасы
Логистика мамандығы

СӨЖ
Тақырыбы: «Бас жиынтық және таңдама»
Орындаған: Садуақас Д. А
Тексерген: Тұраров Д. Р
Алматы қаласы
2019-2020 оқу жылы
Мазмұны:
- Бас жиынтық және таңдама
- Статистикалық мәліметтерді ұсыну мен өңдеудің әдістері
- Таңдаманың сипаттамаларын есептеу
- Нүктелік бағалау және олардың қасиеттері
- Таңдаманы бағалау қасиеттері
- Интервалдық бағалау
- Статистикалық гипотезаларды тексеру
- Гипотезаларды тексеру мысалдары
1. Бас жиынтық және таңдама.
Таңдама жиынтық немесе жай таңдама деп кездейсоқ таңдап алынған обьектілер жиынын айтады.
Бас жиынтық деп ішінен таңдама жүргізілетін обьектілер жиынын айтады. Жиынтық көлемі деп осы жиынтықтың обьектілер санын айтады.
Біртекті обьектілердің жиынтығын оларды сипаттайтын сапалық және сандық белгісі бойынша зерттеу керек болсын. Мысалы, бір партия құралдар бар болса, олардың сапалық белгісі ретінде стандарттылығы сандық белгісі ретінде-құралдың өлшемі қарастырылады. Кей кезде жиынның әр обьектісін қажет белгісіне қатысты зерттеп, жаппай зерттеу жүргізеді. Алайда, практикада мұндай жаппай зерттеу салыстырмалы түрде сирек қолданылады. Практикада таңдаманың түрлі әдістері қолданылады. Бұл әдістерді 2 түрге топтауға болады.
І. Бас жиынтықты бөлшектеп бөлуді қажет етпейтін таңдама, оған:
а) жай кездейсоқ қайталанымсыз таңдама;
б) жай кездейсоқ қайталанбалы таңдама;
ІІ. Бас жиынтық бөлшектеп бөлінетін таңдама, оған:
а) типтік таңдама;
ә) механикалық таңдама;
б) сериялық таңдама
жатады.
Жай кездейсоқ таңдама деп барлық бас жиынтықтан обьектілерді бір-бірден алатын таңдаманы атайды. Егер алынған карточкаларды бумаға қайтармаса, онда таңдама жай кездейсоқ қайталанымсыз болады.
Типтік таңдама деп, обьектілер бас жиынтықтың барлығынан емес, оның әрбір «типтікң бөлігінен алынатын таңдаманы атайды.
Механикалық таңдама деп бас жиынтық таңдамаға қанша обьект қажет болса, сонша топқа бөлінетін таңдаманы атайды, әрбір топтан бір обьект алынады.
Сериялық таңдама деп бас жиынтықтан обьектілерді бір-бірден емес, жаппай зерттеуге ұшырайтын обьектілер «серияларменң таңдап алатын таңдаманы атайды.
Алынған таңдамалық зерттеулерді жүйелендіруде таралудың статистикалық дискретті және интервалды қатарлар қолданылады.
Вариациялық қатар - сәйкес жиіліктерімен бірге ранжирленген ретпен орналасқан белгінің сандық мәндері.
Вариациялық қатар
- варианта, зерттеліп отырған белгінің сандық өрнектелуі;
- вариантаның жиілігі (“салмақ”), оның вариациялық қатарда қайталану саны;
n - бақылаудың жалпы саны, таңдама көлемі (яғни, барлық жиіліктердің қосындысы, n =Σ ) ;
- вариациялық қатарды шектейтін шеткі варианталар, (қатардың лимиттері) ;
- қатардың амплитудасы (яғни, ең жоғарғы және ең төменгі варианталардың айырымы ) .
Вариациялық қатардың қолданылуы:
Вариациялық қатар орта шаманы және әртүрлілік критерийлерін анықтау үшін қолданылады.
Орта шама - зерттеліп отырған белгі өлшемінің жалпылама сипаттамасы. Ол бір санмен сапалы біртекті жиынтықты сандық сипаттауға мүмкіндік береді.
Бас жиынтықтан таңдама алынсын, және х 1 -n 1 рет, х 2 -n 2 рет, . . . , х k -n k рет қайталанады, ал -таңдама көлемі. х 1 мәндерін варианталар деп, ал өсу ретімен жазылған варианталар тізбегін вариациялық қатар деп атайды. Қарастырылатын мәндер санын жиіліктер, ал олардың таңдама көлеміне қатынасын салыстырмалы жиіліктер - деп айтады. Таңдаманың статистикалық таралуы деп варианталар мен оларға сәйкес жиіліктер немесе салыстырмалы жиіліктердің тізімі аталады.
1. Статистикалық таралуды интервалдар тізбегі және оларға сәйкес жиіліктер (интервалға сәйкес жиілік ретінде осы интервалға түскен жиіліктер қосындысын қабылдайды) тізбегі түрінде беруге болады. Мода ( Мо ) - кездейсоқ шаманың ең жиі кездесетін мәні
2. Медиана ( Ме ) - таңдаманы қақ ортасынан бөлетін кездейсоқ шаманың мәні. Барлық мәндерді ранжрленген қатарға орналастыру керек.
Таңдаманың 50% жоғары не төмен орналасқан мәнді көрсетеді.
3. Минимал мәні
4. Максимал мәні
5. Қадам
6. Орташа қатесі (стандартты) - таңдама көрсеткіштің (статистика) оның генеральды параметрінен ауытқу шамасы:
Көптеген кездейсоқ құбылыстардың бағынатын заңдылығын анықтау тәселесі, бақылау нәтижесінің статистикасын зерттейтін ықтималдық теориясының әдістіне негізделгегн.
Математикалық статистииканың мынадайесептерін қарастырамыз:
- Жүргізілген тәжірибенің немесе бақылаудың нәтижесінде, алынған статистикалық мағлұматтарға жинау жән оларды топқа бөлу әдістерін көрсету.
- Зерттеудің мақсатына байланысты статистикалық мағлұматтарға анализ жасау әдістерін іздеп табу.
Математикалық статистиканың міндеті ғылыми және трактикалық тұжырымдар жасау үшін сиатистикалық мағлұматтарды жинау. Кейде қажетті белгісі бойынша, заттар жиынтығындағы әрбір затты түгелдей тексеруге тура ккеледі. Іс жүзінде бұлай түглдей тексеру өте сирек зерттейді. Таңдап алынған жиынтық немесе жай ғана таңдамалы деп, кездейсоқ таңдап алынған заттардың жиынын айтады.
Бас жиынтық
деп, таңдамалы жасалатын заттардың жиынтығын айтады.
Көлем жиынтығы
деп, осы жинақтың ішіндегі заттардың санын айтады. Мысалы, егер 1000 бөлшектен тексеру ғғшін 100 бөлшек бөліп алынса, онда бас жиыниықтың көлемі N=1000, ал таңдамалы жиынтығының көлемі n=100.
Бақылау нәтижесінде қарастырылып отырған белгінің жиынтықтағы, әрдір бірлікке қатысты сандық немесе сапалық өзгерісі туралы мәлімет аламыз. Статистикалық бақылаудың мақсаты сол жиынтықта белгінің өзгеруін (
вариасиясын
) шешу. Ал белгінің мүмкін мәндерін статистикада
варианта
деп атайды. Варианталар сандық (дискретті немесе үздіксіз) болатын мүмкіндігін көрдік. Тәжірибе жүргізілгенде белгі мәндері қалай болса солай орналасуы мүмкін. Мысалы, тексерілген 100 вал диаметрі см-мен 15, 12, 16, 12, 13, 14, 16, 13, 14, 12 болып шықты. Мұны реттеп жазсақ 12, 12, 12, 13, 13, 14, 14, 15, 16, 16 болар еді. Мұны ықшамдап кесте түрінде жазсақ, мынадай болады:
Бұл кестенің жоғарғы жолын белгі мәндері (варианталары), ал төменгі жолында әрбір мәннің неше рет кездескені келтірілген. Осылай реттелген кестені вариацмялық қатар деп атайды.
Әдетте белгіні (вариантаны) кездейсоқ шамалар сияқты х, у, z, . . . , y k , z 1 , z 2 , …., z k арқылы белгілейміз. Варианта қайталап отыруы мүмкін. Ол қайталаулардың абсалютті санын (жиілігін) n 1 , n 2 … n k деп белгілесек, онда вариациялық қатардың жалпы түрін мына кесте көрсетеді.
2 - кесте
Мұнда, х і - варианталары сәйкес;
n
i
-жиіліктер;
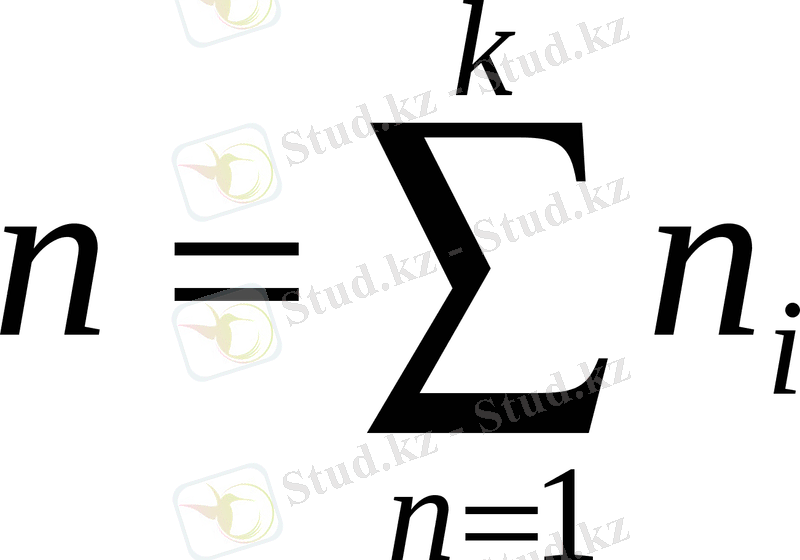 - вариация қатардың көлемі.
- вариация қатардың көлемі.
Іс жүзінде варианта абсалютті жиілікпен қатар салыстырмалы жиілік түрінде де беріледі. Бұл жағдайда 2 кесте былай жазылады:
3 - кесте
Мұндағы,
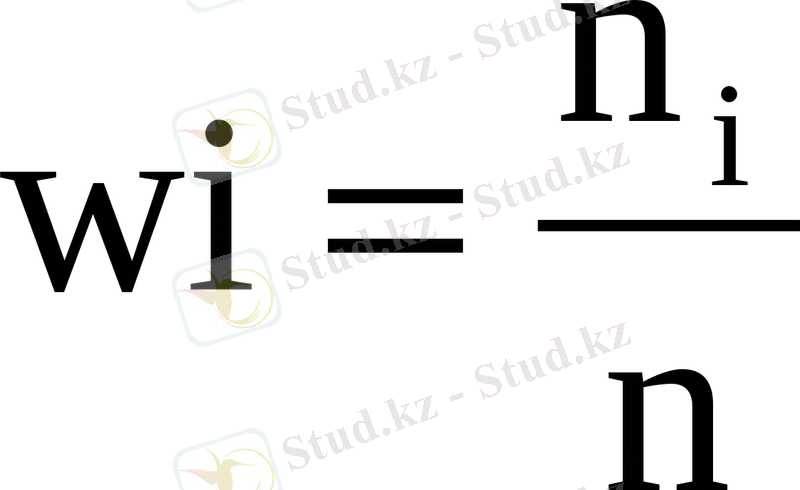 - салыстырмалы жиілік
- салыстырмалы жиілік
ал,

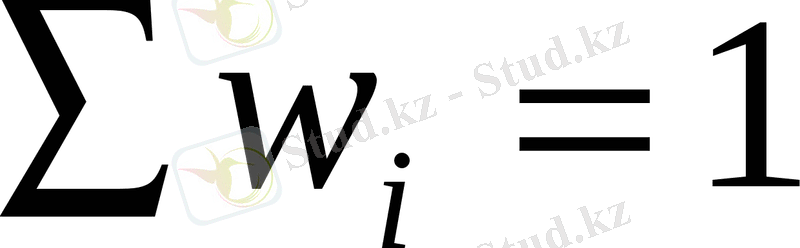 - салыстырмалы жиіліктердің қосындысына тең бірге
- салыстырмалы жиіліктердің қосындысына тең бірге
Егер вариациа үздіксіз өзгеретін болса, онда вариациалық қатарды интервалдар бойынша құруға тура келеді.
Жалпы түрде интервалдық қатар мынадай болады:
4 - кесте. Жиіліктің интервалдық түрі.
немесе
5 - кесте. Салыстырмалы жиіліктің интервалдық түрі.
Мұндағы (x 1; x 2 ), (x 2; x 3 ), (x 3; x 4 ) . . . , (x m; x m+1 ) аралықтары белгінің мүмкін мәндері жататын интервалды к 1 = x 2 -x 1 ; к 2 = x 3 -x 2 , к m = x m+1 -x m - айырымдары интервалды сипаттайды.
а) Шарттық варианталар.
Делік, таңдама варианттарлары өспелі ретінде орналасқан, яғни вариациялық қатар түрінде.
Айырымы h - қа тең арифметикалық прогрессияны құрастыратын варианталарды бірдей қашықтықтағы варианталар деп атайды.
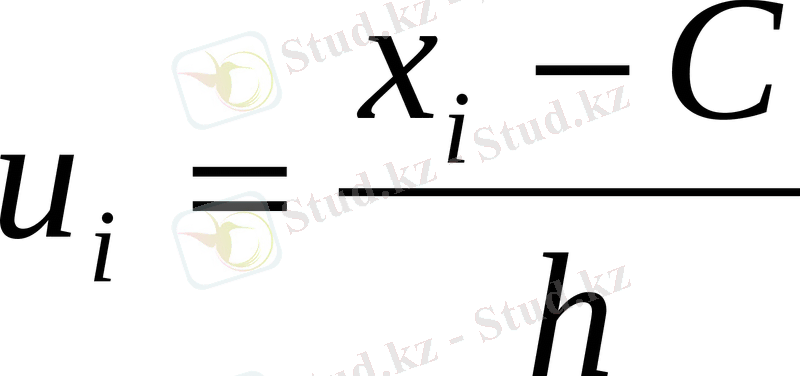 формуламен анықталатын вариантталарды шарттық варианта
деп атайды.
формуламен анықталатын вариантталарды шарттық варианта
деп атайды.
Мұндағы С - жалған ноль (санақтың жаңа бастамасы) .
Һ - қадам (екі көрші варианталардың айырмасы) .
Алғашқы варианталарды шарттық варианталарға ауыстыруы, ықшамдалған әдістер таңдамының жинақты сипаттамаларын есептеу үшін негізделген.
б) Таңдамалы орта мен дисперсияны есептеу көбейтінді әдісін қарастырайық. Делік, таңдама бірдей қашықтықтағы варианталар және оларға сәйкес жиіліктер түрінде берілсін. Бұл жағдайда таңдамалы ортаны және дисперсияны көбейту әдісі формулаларымен табу қолайлы.
Яғни,
 -таңдамалыорта
-таңдамалыорта
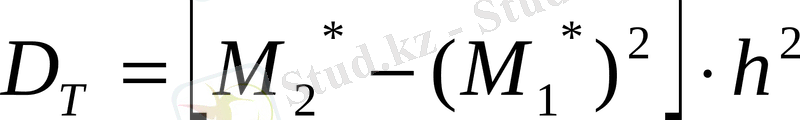 - таңдамалы дисперсия
- таңдамалы дисперсия
Мұндағы һ - қадам
С -жалған ноль(ең үлкен жиілігі бар варианта) .
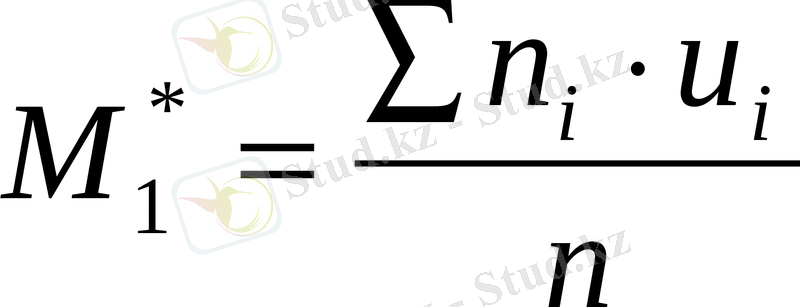 -.
-.
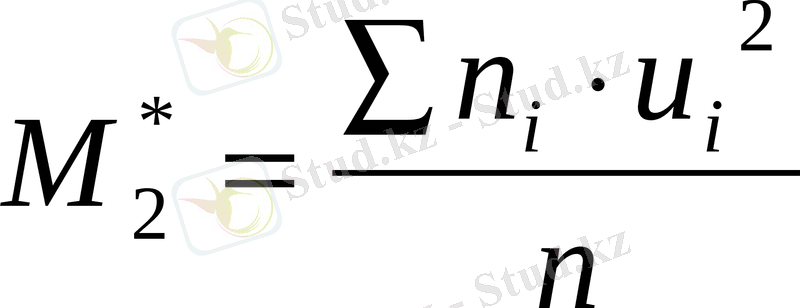 - екінші ретті шарттық сәт.
- екінші ретті шарттық сәт.
Көбейтінді әдісін қолдауын бір мысалда қарастырайық.
Мысал. Көлемі n=100 берілген үлестірімнің таңдамалы орта мен дисперсиясын табыңыз.
х і
n i
Шешуі. Бірінші есептеу кестені құрамыз; Ол үшін:
- Варианталарды бірінші бағанға жазамыз.
- Жиіліктерді екінші бағанға жазамыз, жиілік қосындысын (n=100) екінші бағанның төменгі торшасына жазамыз.
- Жалған ноль (С) ретінде С=16 вариантаны аламыз, оның ең үлкен жиілігі бар (С ретінде бағаның ортасында тұрған әлде қандай вариантаны алуға болады) . Жалған ноль тұрған жолдың үшінші бағанның торшасына 0 жазамыз, оның үстінен тізбектеп - 1, -2 - жазамыз, ал о - дың астына 1, 2, 3 жазамыз.
- Жиіліктердің шарттық төртінші бағанға жазамыз, ал олардың қосындысынбағанның төменгі торшасына орналастырамыз.



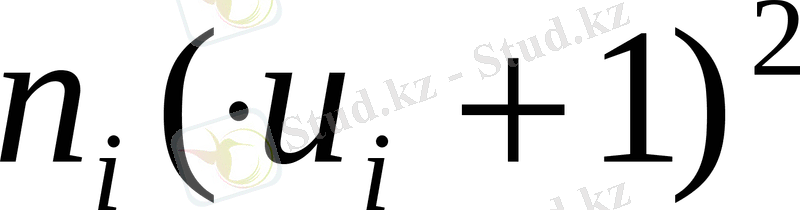
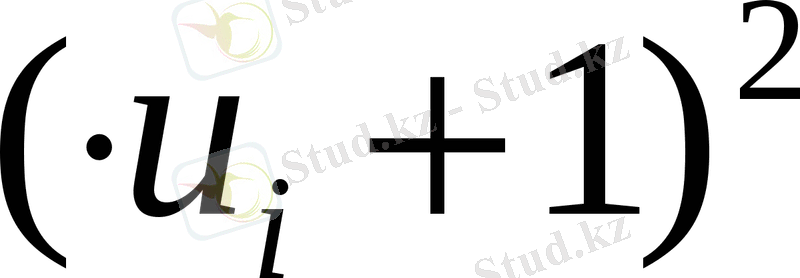
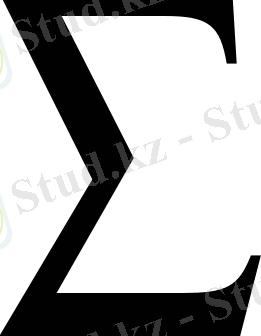

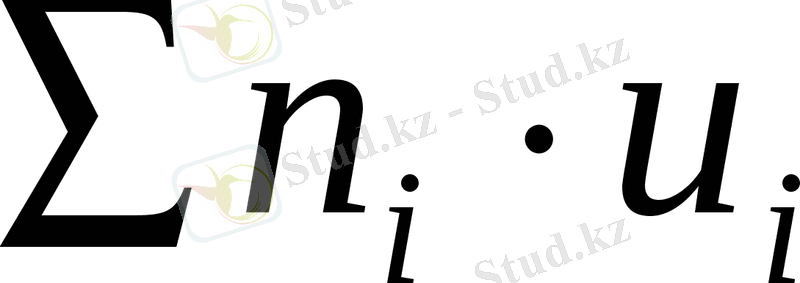 =23
=23
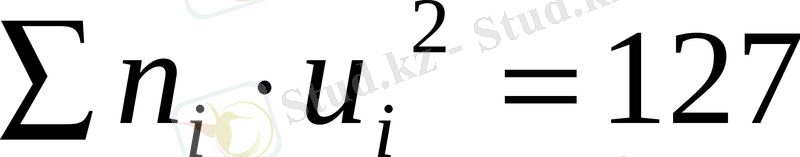
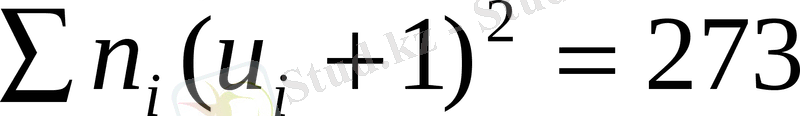
Бақылау:
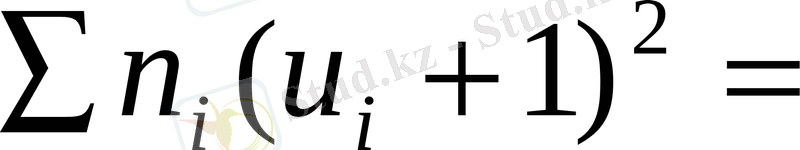


273=127+2*23+100
273=127+146
273=273
5) Жиілікті шарттық варианталардың квадраттарына көбейтіп шыққан көбейтінділерді
 бесінші бағанға жазамыз, шыққан сандарды қосып, олардың қосындысын
бесінші бағанға жазамыз, шыққан сандарды қосып, олардың қосындысын
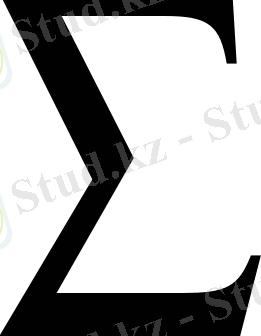
 бағанның төменгі торшасына орналастыр-
бағанның төменгі торшасына орналастыр-
ады.
6) Шарттық ықтималдылықтарды 1 санына үлкейтіп және олардың квадраттарын сәйкес жиеліктерге көбейтіп
 көбейтіндіні алтыншы бақылау бағанға жазамыз; барлық шыққан сандарды қосып, олардың қосындысын
көбейтіндіні алтыншы бақылау бағанға жазамыз; барлық шыққан сандарды қосып, олардың қосындысын
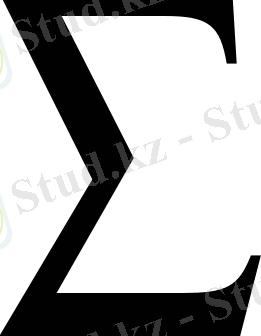
 бағанның төменгі торшасына орналастырамыз.
бағанның төменгі торшасына орналастырамыз.
Қорытындыда 1-ші кесте шығады.
Бақылау үшін мына теңбе-теңдікті қолданамыз:
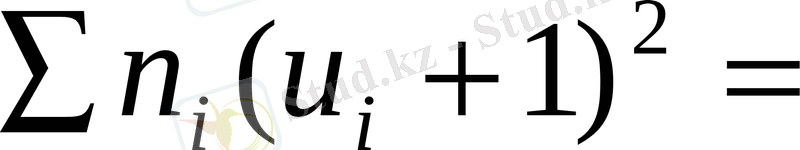


Бақылау:
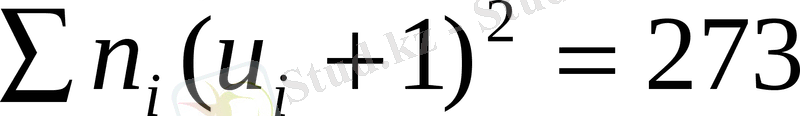 ;
;

 =127+2*23+100
=127+2*23+100
Бақылау қосындылардың дәл келу есептеуінің дұрыс болу куәлігі. Бірінші және екінші ретті шарттық сәттерді есептейміз.
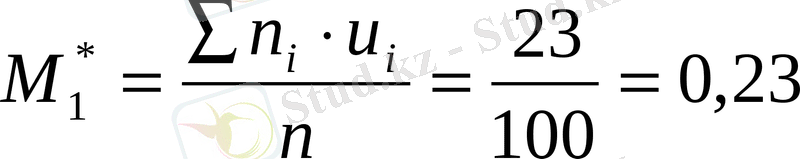
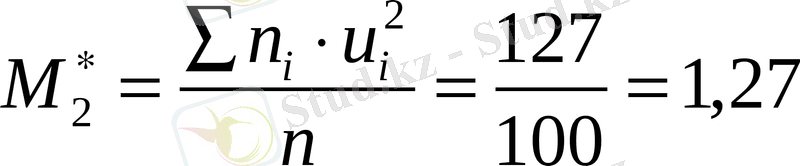
Қадамын табайық һ=14 - 12=2
Жалған ноль С=16 еске алып, таңдамалы орта мен дисперсияны есептейміз.
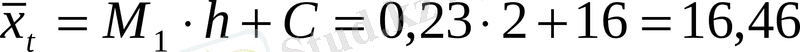

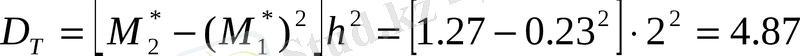
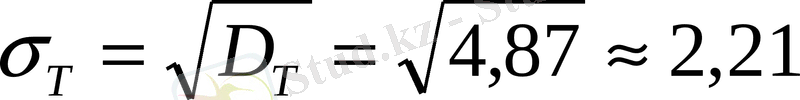
Сенімділік интервалды анықтайық (
 -
-
 ;
;
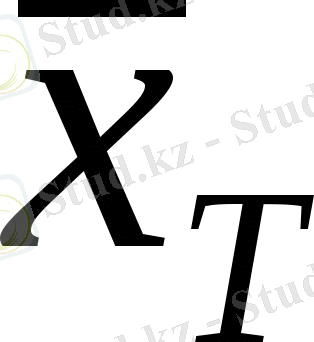 +
+
 ) ; мұндағы
) ; мұндағы
 - бағаны мына формуламен анықтаймыз
- бағаны мына формуламен анықтаймыз
 =
=
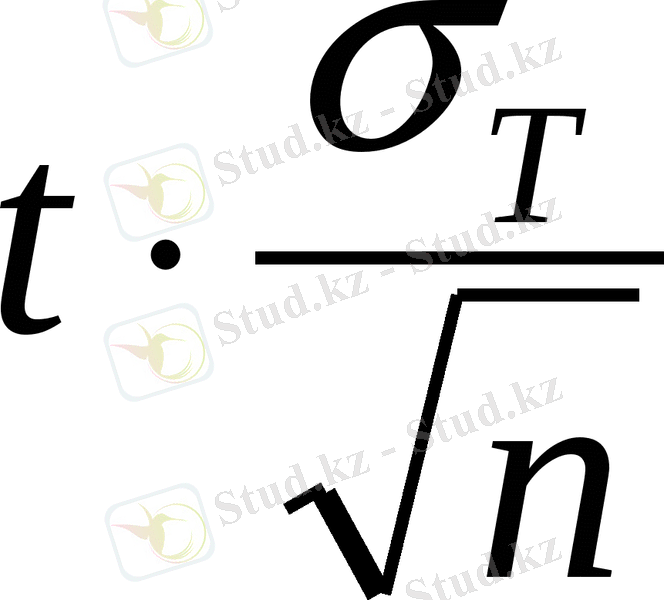 , ал t параметрді
, ал t параметрді
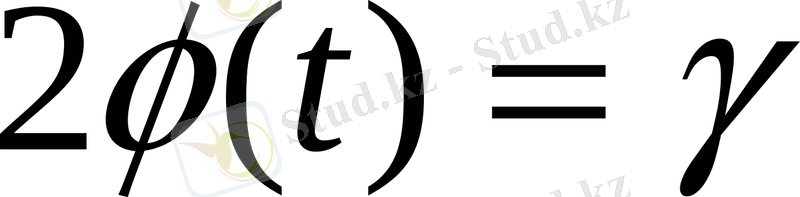 қатынасын табамыз.
қатынасын табамыз.
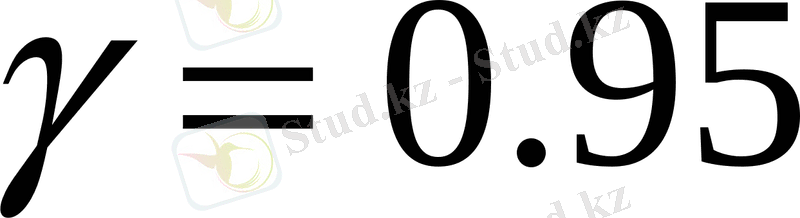 сенімділігі бар жиынтықтың белгісіз математикалық күтімін
а
бағалау үшін _ сенімділік интервалды табамыз. Сонымен
сенімділігі бар жиынтықтың белгісіз математикалық күтімін
а
бағалау үшін _ сенімділік интервалды табамыз. Сонымен
 ;
;
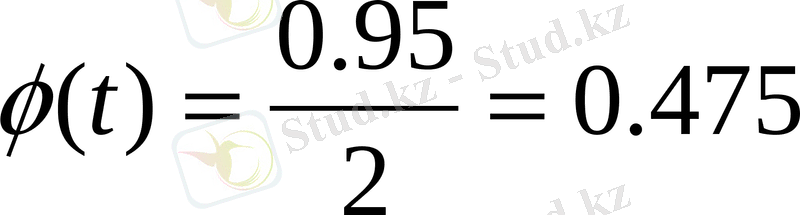 ; (екінші кестеден t=1. 96) енді баға
; (екінші кестеден t=1. 96) енді баға
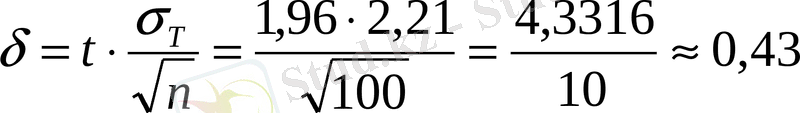
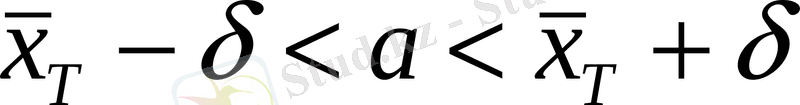 ;
16, 46-0, 43<a<a
;
16, 46-0, 43<a<a
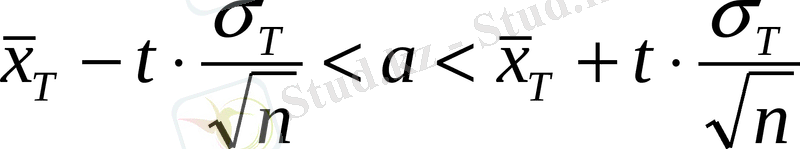 немесе
немесе
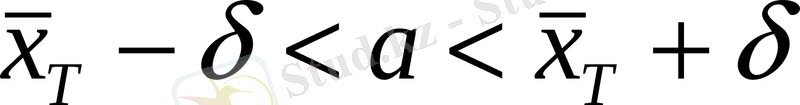 </a
</a
2. Статистикалық мәліметтерді ұсыну мен өңдеу әдістері
Статистикада біз жиі қолданылатын статистикалық әдістерді бөлеміз олардың арасында: сипаттау статистикасы; эксперименттерді жобалау; таңдау; гипотезаларды тексеру; регрессиялық, корреляциялық және факторлық талдау; уақытша қатарларды талдау ; статистикалық берілген рұқсатнамалар; өлшеу дәлдігін талдау; статистикалық технологиялық процестерді басқару; процестерді статистикалық бақылау; сенімділікті талдау;
Экономикада статистикалық әдістерді қолдану маңызды рөл атқарады, өйткені оләлеуметтік-экономикалық мәселелер бойынша ақпараттың үлкен көлемін өңдеумен және талдаумен айналысады құбылыстар, өз кезегінде, Экономикалық зерттеулер экономикалық процестің деңгейі мен динамикасын анықтайтын факторлар. Бір қызығы, бұл массаның сандық сипаттамаларын зерттейтін экономикалық статистика талдау және статистикалық мәліметтер көмегімен экономикадағы құбылыстар мен процестер өңдеу. Оның негізгі әдістері сипаттама, талдау және салыстырмалы әдістер болып табылады.
Әрбір жаңа статистикалық әдіс алдыңғысының негізінде іске асырылады. Мысалы, корреляцияны меңгеру мүмкін емес вариацияларын зерттеу әдістері, сондай-ақ вариацияларды зерттеу орташа шамаларды зерттемей мүмкін емес және т. б.
Егер маңыздылығы жалпы бағаланған ғылыми нәтижелер болса
а) типті жұмыстарға сәйкес келетін ғылыми өлшемдер, онда с) негізгі міндет қызметтің белгілі бір саласындағы нақты міндеттерді табысты шешу болып табылады. қолдану (техника және технология, экономика, әлеуметтану, медицина және т. б. ) Б) типті туындылар аралық орын алады, өйткені бір жағынан, қасиеттері мен статистикалық әдістері мен модельдерін теориялық зерттеу нақты қосымшалар өте күрделі және математикалық болуы мүмкін алайда нәтижелер жалпы қызығушылық білдірмейді және тек команда үшін өзекті болуы мүмкін бейінді мамандар. Жұмыстың түрі Б) шешім қабылдауға бағытталған деп айтуға болады нақты қосымшаның жалпы міндеттері. Сипаттамалық статистика әдістері негізінен, а), аналитикалық статистиканың әдістері б) - с типтері деп аталады) тиісінше. Ғылыми зерттеулерде статистикалық әдістерді қолданудың жалпы алгоритмі келтірілген.
1) ғылыми зерттеу мәселелері негізінде гипотезаны қалыптастыру;
2) зерттеуге қажетті параметрлердің санын анықтау (сипаты)
тестіленетін статистикалық атрибут, деректер типі, тарату түрі) ;
3) зерттеудің статистикалық мақсаттарын анықтау;
4) статистикалық әдістерді таңдап алынған параметрлерге
зерттеудің статистикалық мақсаттары;
5) алдымен статистикалық қорытынды жасап, содан кейін тәжірибелік
бақылау.
Зерттеудің негізгі статистикалық міндеттері (3-кезең) :
а) зерттелетін статистикалық белгі деңгейіндегі айырмашылықтарды анықтау;
б) деңгей ауысуының маңыздылығы мен бағытын анықтау
зерттелген ерекшелігі;
в) статистикалық белгіні бөлудегі айырмашылықтарды анықтау;
d) статистикалық сипаттамалардың өзгеруі арасындағы Келісімді анықтау;
г) статистикалық сипаттаманың өзгеруін анықтау бақыланатын жағдайлар (факторлар) ;
д) бүкіл әлемдік бас жиынтықтағы объектілерді біртекті топ;
g) өмір сүру туралы деректерді талдау.
Зерттеу нәтижелерін өңдеудің статистикалық әдісін таңдау туралы шешімдеректер алынған кезең (4-кезең)
1) А сәйкес статистикалық есептің түрін анықтау (a) ÷ x) )
2) статистикалық ақпаратты таңдау алгоритмін қолдануға;
Алдымен біз статистикалық есептерді және оларға қолданылатын статистикалық әдістерді жүйелейміз. Ол үшін таңбалар тізімін енгіземіз:
F-Фишер дисперсиясының коэффициенті;
G-сынақ белгісі;
H-Крускал-Уоллис сынағы;
L-бет трендінің талдауы ;
Q-Розенбаум тест ;
S-Jonckheere тренд сынағы;
Test-Уилкоксон т тесті;
т-т-Стьюдент өлшемі ;
U-Манн-Уитни U-тест;
хи-квадрат сынағы;
Р-Фридман өлшемі ;
λ-Колмогоров-Смирнов сынағы;
φ* - бұрыштық түрлендіру Фишердің
rxy-Пирсон корреляция коэффициенті, ;
RS-Спирмен рангалық корреляция коэффициенті;
R-бисериалды корреляциялық тест;
τ-Кендалл Тау рангтік корреляция коэффициенті;
φ-коэффициенті Пирсон.
Мысалы
Корреляция коэффициентін есептеуге арналған деректер
Гипотезаны тексеру үшін статистикалық есепті таңдаймыз-бұл "g) " (анықтама статистикалық куәліктердің келісілуі) . Бұдан әрі біз алгоритмді ұстанамыз:
статистикалық белгіні бөлу маңызды емес, олардың екеуі сапалы түрі, міндеті " g) ", сондықтан біз тиісті коэффициентті қолданамыз корреляция( немесе Қауымдастық φ) :
φ =2∙18-10∙6/√12∙24∙8∙28= -0, 094.
Енді біз бағалаймыз коэффициенттің алынған мәнінің мәні. Бұл үшін өлшем мәні 𝑥 р 2 = nФ2
Х 2 = 36·(-0, 094) 2 = 0, 321.
0, 05 мәнділік деңгейі және Саны үшін еркіндік дәрежесі 1. Содан кейін біз Х 2 (0, 05; 1) = 3, 841,
0, 321 < 6, 635, онда алынған мән елеусіз болып есептеледі
3. Таңдаманың сипаттамаларын есептеу
Егер жиіліктері
n
1
, n
2
, . . . , n
m
болатын
х
1,
х
2
, . . . , х
m
вариациялық қатар берілсе, онда
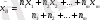 теңдігімен анықталатын
теңдігімен анықталатын
 шамасын вариациялық қатардың
арифметикалық ортасы
деп атайды, мұндағы
n = n
1
+ n
2
+ n
3
+ . . . + n
m
шамасын вариациялық қатардың
арифметикалық ортасы
деп атайды, мұндағы
n = n
1
+ n
2
+ n
3
+ . . . + n
m
Таңдама Х белгісінің жиілігі вариациялық қатардың үлестіру заңы бойынша берілсін.
мұнда
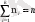
Вариациялық қатардың сандық сипаты немесе параметрі болып мынадай қосындыларды айтады.
Таңдаманың арифметикалық орта мәні деп мынадай шаманы айтамыз
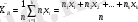
Орта шаманы экономикалық мәліметтерді өңдеу кезінде қолданылады.
Х белгісінің мәндерінің дисперсиясы деп мәні оның арифметикалық ортаға қатысты мынадай шаманы айтады
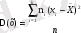 (3)
(3)
Ал, дисперсиядан алынған квадрат түбір орта квадраттық ауытқу деп аталады
 (4)
(4)
Таңдаманың дисперсиясы мен арифметикалық ортаның қасиеттері
1-қасиет. Егер вариантты бір тек бір санға еселеп арттырса (кемітсе), онда арифметикалық орта сонша есе артады (кемиді),
 (5)
(5)
2-қасиет. Егер барлық варианттардан бір тек бір санды шегерсе (қосса), онда арифметикалық орта сол санға кемиді (өседі), яғни
 (6)
(6)
3-қасиет. Егер барлық варианттарды к рет арттырса (кемітсе), онда дисперсия к 2 рет артады (кемиді), яғни
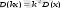 (7)
(7)
4-қасиет. Егер варианттарды бір тұрақты шамаға өсірсе немесе кемітсе, онда дисперсия өзгермейді, яғни
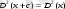 (8)
(8)
5-қасиет. Егер жиіліктерді бірдей санға арттырса немесе кемітсе, онда дисперсия өзгермейді.
6-қасиет. Дисперсия варианталардың квадраттарының арифметикалық ортасы мен арифметикалық ортаның квадратының айырмасына тең, яғни
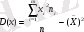 (9)
(9)
Осы қасиеттерді пайдалана отырып, арифметикалық ортаны келесі формула бойынша табуға болады
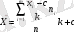 (10)
(10)
Ал дисперсияны мына формула бойынша есептейді
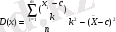 (11)
(11)
Бұл формулалар арифметикалық есептеулерді анағұрлым жеңілдетеді. Мұндағы к және с кез келген тұрақты. Әдетте, с ретінде берілген қатардың ортасында орналасқан жиілігі ең жоғары вариантаны алады. Ал к ретінде x i -c айырымының ЕҮОБ-ін алады.
3-мысал.
Кәсіпкер өзінің қаражатын тең бөліп екі шартқа отырды, әрбіреуі оған
100
пайыз кіріс әкеледі. Әрбір шарттың «күйремеу» ыктималдықтары 0, 8 тең. Шарттың уақыты өткеннен кейін кәсіпкер ең болмағанда ештеңесін жоғалтпау (өзінің қаражатын сақтап қалу) ықтималдығықандай?
Шешуі. Егер шарттың біреуі «күйремесе» (себебі екінші шарт шығынды жабады), немесе екі шарт та орындалса, онда кәсіпкер кем дегенде өзінің қаражатын сақтап қалады яғни шығынға ұшырамайды.
 және
және
 оқиғалары - сәйкес шарттардың орындалуы болсын, ықтималдықтары р=0, 8, бұл оқиғалар бір-бірінен тәуелсіз. Ал оларға қарама-қарсы оқиғалар
оқиғалары - сәйкес шарттардың орындалуы болсын, ықтималдықтары р=0, 8, бұл оқиғалар бір-бірінен тәуелсіз. Ал оларға қарама-қарсы оқиғалар
 және
және
 - шарттардың орындалмауы q=0, 2. Онда
- шарттардың орындалмауы q=0, 2. Онда
 оқиғалары үйлесімсіз болады. Бұл ықтималдықты мына формула бойынша табамыз (мұндағы
оқиғалары үйлесімсіз болады. Бұл ықтималдықты мына формула бойынша табамыз (мұндағы

 - екі шарттың да орындалуы)
- екі шарттың да орындалуы)
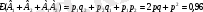 .
.
4. Нүктелік бағалау және олардың қасиеттері
Тәжірибеден алынған мәліметтер бойынша кездейсоқ шамалардың үлестіруін және оның параметрлерін анықтайтын математикалық аппарат қажет. Сайып келгенде математикалық статистика әдістерінің мақсаты статистикалық мәліметтерді жинастыру, оларды өндеу, белгісіз бас жиынтық үлестіріуінің параметрлерін және белгісіз үлестіру функцияларын бағалау, сондай-ақ парамерлер мен үлестірулер жайындағы статистикалық гипотезалардың дұрыстығын тексеру болмақ. Статистикалық әдістер белгінің сандық түріндегі ғана қолданылады. Ал белгі мәні болса санмен өлшенуі де мүмкін, сапалық болуы да мүмкін. Егер бас жиын шексіз немесе өте көп болса, ондай зерттеу ушін алынған оның бөлігін
таңдама жиынтық
дейді. Бас жиын параметрін
 десек, ал таңдама параметрін
десек, ал таңдама параметрін
 десек, онда бағасы ретінде қарастырады
десек, онда бағасы ретінде қарастырады
 қаншалықты
қаншалықты
 -ға жуық екенің білуді айқындау үшін математикалық аппаратты қолдану керек.
-ға жуық екенің білуді айқындау үшін математикалық аппаратты қолдану керек.
Үлестірудың әрбір параметрі шектіматериал көлемінде есептелгендіктен әруақытта кездейсоқтық элементі болады. Сондықтан бул мәнді зерттеп отырған бас жиынды сипаттайтын параметр мәнімен тепе-тең деп қарастыруға болмайды. Демек
 -ны тек
-ны тек
 мәнінің бағасы деп қарастыру керек. Ал
мәнінің бағасы деп қарастыру керек. Ал
 -ны бір ғана санмен бағаландықтан, мұндай бағалауды
нүктелік бағалау
деп атайды. Ал нүктелік баға Х кездейсоқ шама болғандықтан
-ны бір ғана санмен бағаландықтан, мұндай бағалауды
нүктелік бағалау
деп атайды. Ал нүктелік баға Х кездейсоқ шама болғандықтан
 -ға қатысты әртүрлі ауытқулар беруі мүмкін. Сондықтан, зерттелген таңдамалардың
-ға қатысты әртүрлі ауытқулар беруі мүмкін. Сондықтан, зерттелген таңдамалардың
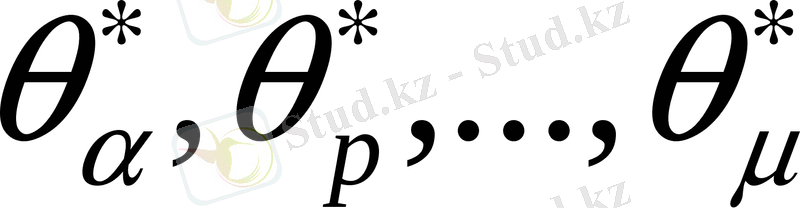 параметрлерінің ішінең
параметрлерінің ішінең
 қатысты ең аз ауытқу беретін және
қатысты ең аз ауытқу беретін және
 -ны жақсы бағалайтын
-ны жақсы бағалайтын
 -ті таңдап алатын критерийді табу керек. Ол үшін төмендегі үш жұмыс орындауға тиісті:
-ті таңдап алатын критерийді табу керек. Ол үшін төмендегі үш жұмыс орындауға тиісті:
1.
 -ға ең жуық мән беретін
-ға ең жуық мән беретін
 бағасына қойылатын талаптарды анықтау;
бағасына қойылатын талаптарды анықтау;
2. Бағаларды табу әдістерін анықтау;
3. Бас жиын параметрлері сенімді қортынды алу үшін бұл бағаларды пайдалану мүмкіндіктерін көрсету.
6. Интервалдық бағалау
Интервалдық бағалар. Бір санмен ғана анықталатын нүктелік баға таңдаманың көлемі аз болғанда, өрескел қателерге әкелуі мүмкін. Сондықтан бас жиынның белгісіз бағасын, яғни θпараметрі жататындайαβ интервалын белгілі бір сенімділікпен айқындау мәселесін қарастырайық.
θ параметрінің бағасы бойынша θ
*
сенімділік ықтималдығы деп׀θ-θ*׀‹δ теңсіздігініңорындалу ықтималдығыγ- ны атайды, яғни p= ׀θ-θ*׀‹δ=γ, бұл жердеδ бағаның дәлдігі.
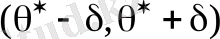 интервалын
интервалын
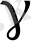 сенімділікпен алынған сенімділік интервалы деп атайды.
сенімділікпен алынған сенімділік интервалы деп атайды.
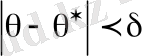 ,
,
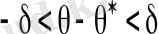 ,
,
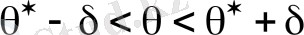
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz