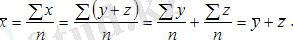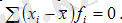Орташа шаманың маңызы мен түрлері: есептеу әдістері және қолдану шарттары


Орташа шаманың маңызы мен негізі, пайдалану шарты . Орташа шама ның түрлері және есептеу жолдары.
Жоспар
Кіріспе
Негізгі бөлім
1. Орташа шаманың түрлері мен есептеу әдістері.
1. 1Арифметикалық орташа шама бойынша жалпы түсінік.
1. 2 Құрылымдық орташа шаманың Мода және Медиананы бөліп қарастыру.
1. 3Үйлесімдік орташа шаманың ерекшеліктері.
Қорытынды
Пайдаланылған әдебиеттер тізімі
Кіріспе
Орташа шама деп - біртектес жиынтықты белгілі бір жағдайда және бел гілі бір уақытта өздеріне тән белгіс бойынша жинақтап көрсететін орташа сан мөлшерін, яғни біртектес жиынтық бірліктеріне жатқызылатын сандық шама сын айтады. Орташа мән зерттелетін популяциядағы белгінің немесе белгілер тобының жалпыланған мәнін сипаттайтын көрсеткіш деп аталады.
Егер біз агрегатты сапалы біртекті белгілермен зерттейтін болсақ, онда орташа мән мұнда типтік орташа мәннің типтік мәні ретінде пайда болады. Мысалы, белгілі бір салада жұмыс істейтін жұмысшылар тобы үшін тұрақты кіріс деңгейі анықталады, яғни негізгі қажеттіліктердің орташа құны анықталады, яғни. типтік орта белгілі бір популяциядағы атрибуттың сапалық біртекті мәндерін жинақтайды, бұл осы топтағы жұмысшылардың қажетті тауарларға кететін шығындарының үлесі.
Сапалық ерекшеліктері бар агрегаттарды зерттеу кезінде орташа көрсеткіштердің алдын-ала көрінуі мүмкін. Мысалы, бұл жан басына шаққандағы ұлттық табыстың орташа көрсеткіштері (әр түрлі жас топтары), бүкіл Қазақстан бойынша дәнді дақылдардың орташа өнімділігі (әр түрлі климаттық аймақтар мен әртүрлі дақылдардың аудандары), елдің барлық өңірлері үшін орташа өнімділік деңгейі, орташа белгілі бір кезеңдегі температура және т. б.
Мұнда орташа шамалар атрибуттардың немесе жүйелік кеңістіктік агрегаттардың (халықаралық қауымдастық, континент, мемлекет, аймақ, аймақ және т. б. ) немесе уақыт бойынша динамикалық агрегаттардың сапалық гетерогенді мәндерін жинақтайды. Мұндай орташа көрсеткіштер «Жүйелік орташа» деп аталады.
Сонымен, орташа мәндердің мәні олардың жалпылау функциясынан тұрады. Орташа мән сипаттаманың көптеген жеке мәндерін алмастырады, популяцияның барлық топтарына тән жалпы қасиеттерді ашады. Бұл өз кезегінде кездейсоқ себептерден аулақ болуға және жалпы себептерге байланысты жалпы заңдылықтарды анықтауға мүмкіндік береді.
Орташа мән бүкіл ақпаратқа жалпылама сандық сипаттама береді және оны осы белгімен байланысты сипаттайды. Орташа жалақы қарастырылған жұмысшылардың жалақысының жағдайына жалпы сандық сипаттама береді. Сонымен қатар, орташа мәндерді қолдана отырып, әртүрлі ақпарат жинақтарын салыстыруға болады. Мәселен, сіз әртүрлі ұйымдарды еңбек өнімділігі, сонымен қатар капитал өнімділігі, материалдық өнімділік және басқа көрсеткіштер бойынша салыстыра аласыз.
Орташа шама дұрыс есептеу мен пайдаланудың маңызды шарттары:
- әр нақты жағдайда, орташа сипаттаманың сапалық мазмұнына сүйене отырып, зерттелетін сипаттамалар мен есептеу үшін қол жетімді деректердің байланысын ескеру қажет;
- орташа мәндер есептелетін жеке шамалар біртекті популяциямен байланысты болуы керек және олардың саны маңызды болуы керек;
1. Орташа шаманың түрлері мен есептеу әдістері
1. 1Арифметикалық орташа шама бойынша жалпы түсінік.
Статистикалық өңдеу сатысында әр түрлі зерттеу міндеттерін қоюға болады, оларды шешу үшін сәйкес орташа мәнді таңдау қажет. Бұл жағдайда келесі ережені басшылыққа алу керек: орташа мәннің алымы мен анықтауышын білдіретін шамалар логикалық өзара байланысты болуы керек.
Статистикалық орташа шама түрлері:
- арифметикалық шама;
- құрылымдық шама;
- үйлесімдік шама;
Орташа арифметикалық шама - бұл анықталған ортадағы анықтаманың жиынтық көлемі деректер жиынында берілген барлық бірліктер арасында біркелкі бөлінетін орташа шама . Сонымен, бір жұмысшының орташа жыл дық шығарылымы - егер өнімнің барлық көлемі ұйымның барлық қызмет керлері арасында бірдей бөлінсе, әр жұмысшыға келетін өндіріс көлемінің мәні. Орташа қарапайым арифметикалық шама мына формула бойынша есептеледі:
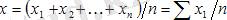
Х- орташа шама;
n - белгілердің саны;
Sx - жиынтық белгісі, яғни х-тің қосындысы;
Орташа арифметикалық шама - сандық белгінің жеке мәндерінің қосындысының жиынтықтағы белгілер санына қатынасына тең:
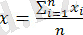
Егер мәліметтер жиынының көлемі үлкен болса және бөлу қатарын білдірсе, онда орташа арифметикалық шама есептеледі. Бұл өнім бірлігіне өлшенген орташа бағаны анықтайды, өнімнің жалпы құны (өнімнің бірлігінің бағасына оның санындағы өнімдердің қосындысы) өнімнің жалпы санына бөлінеді. Мұны келесі формула түрінде қолданылады:
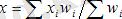
Салмақталған арифметикалық шама барлық белгілердің жиіліктерінің қосындысы қатынасына таңбаның қайталану жиілігіне көбейтіндісінің қаты насы зерттелген жиынның варианттары бірнеше рет кездескен кезде қолда нылады.
Аралық қатар үшін арифметикалық орта шамалар.
Аралық қатарлары үшін арифметикалық ортаны есептеу кезінде алды мен әрбір интервалдың орташа мәнін жоғарғы және төменгі шекаралардың жартылай қосындысы, содан кейін бүкіл қатардың орташа шамасын анықта ңыз. Ашық интервалдар жағдайында төменгі немесе жоғарғы интервалдар дың мәні оларға жақын орналасқан интервалдардың мөлшерімен анықта лады. Арифметикалық орта оның мәнін неғұрлым толық ашатын және есеп теуді жеңілдететін бірқатар қасиеттерге ие:
- Жиіліктердің қосындысы бойынша орташа көбейтінді әрдайым жиіліктер бойынша варианттың көбейтіндісіне тең болады, яғни.
- Әр түрлі шамалардың қосындысының арифметикалық орташа мәні осы шамалардың арифметикалық орташа шамасының қосындысына тең
- Белгінің жеке мәндерінің орташа мәннен ауытқуының алгебралық қосындысы нөлге тең
- Опциялардың квадраттық ауытқуларының мәні орташа мәннен квадраттық ауытқулардың қосындысынан кем, яғни:
- Егер сериялардың барлық нұсқалары бірдей санға азайтылса немесе көбейтілсе, онда орташа мәні сол санға азаяды:
1. 2 Құрылымдық орташа шаманың Мода және Медиананы бөліп қарастыру
Статистикадағы орташа мәндерінен басқа, мода мен медианмен көрсетілген құрылымдық орташа шама өзгеретін сипаттаманың және ішкі құрылымның көлемінің салыстырмалы сипаттамалары үшін қолданылады.
Мода - бұл сериялы шаманың ең көп таралған нұсқасы. Мода, мысалы, сатып алушылар арасында үлкен сұранысқа ие киім, аяқ киім мөлшерін анықтауда қолданылады. Дискреттік сериялардың модасы - бұл ең жоғары жиіліктегі опция. Вариативті қатарлар үшін режимді есептеу кезінде алдымен модальді интервалды (максималды жиілік бойынша), содан кейін модальдік сипаттаманың мәнін мына формула бойынша анықтау керек:
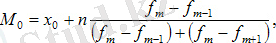
Mo - мода құндылығы;
Xo - модальды интервалдың төменгі шекарасы;
h- аралық шама;
fm - модальді интервал жиілігі;
fm-1 - модаль алдындағы аралықтың жиілігі;
fm+1 - модальдан кейінгі аралықтың жиілігі;
Мысалы, компанияда 16 адам жұмыс істейді: олардың 4-уі - 1 жыл, 3 адам - 2 жыл, 5 адам - 3 жыл және 4 адам - 4 жыл. Осылайша, Мо = 3 жыл модальды тәжірибе, өйткені бұл мәннің жиілігі максималды (f = 5) .
Егер Х тең аралықпен берілсе, онда модальды интервал алдымен f ең жоғары жиіліктегі интервал ретінде анықталады. Осы аралықта режимнің шартты мәні формула бойынша табылады:
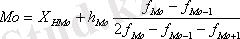
Медиан - бұл сараланған қатарлардың негізін құрайтын және осы серияларды бірдей мөлшердегі екі бөлікке бөлетін атрибуттың мәні. Жиіліктер болған кезде дискретті қатардағы медиананы анықтау үшін алдымен жиіліктердің жарты сомасы есептеледі, содан кейін нұсқаның оған қандай мәні түсетіні анықталады. Егер сұрыпталған серия тақ функция лардың санына ие болса, онда медианалық формула бойынша есептеледі:
Me = (n (жиынтықтағы функциялар саны) + 1) / 2,
Егер белгілер жұп болған жағдайда, медиан жолдың ортасында орналасқан екі белгінің орташа мәніне тең болады.
Вариациялық интервалдарының қатарына медиананы есептеу кезінде алдымен медиананың орналасқан интервалын, содан кейін формуламен медиананың мәнін анықтаңыз:
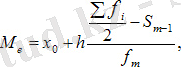
Me - медиан ;
Xo-Медианы бар интервалдың төменгі шекарасы;
h- аралық мән;
Efi - жиіліктердің қосындысы немесе серия мүшелерінің саны;
Sm-l - медиананың алдындағы аралықтардың жинақталған жиіліктерінің қосындысы;
fm - медианалық интервалдың жиілігі;
Статистикалық медиан - X мәні, ол өсу немесе кему реті бойынша реттелген статистикалық популяцияны екі тең бөлікке бөледі. Нәтижесінде жартысының медианасына қарағанда үлкен мәні бар, ал екінші жартысында кіші медиана болады.
Егер X өздігінен белгіленсе, онда медиананы анықтау үшін барлық мәндер өсу реті бойынша 0-ден N-ге дейін нөмірленеді, N жұп санының медианасы Х ортасында 0. 5N және (0. 5N + 1) сандары бар, ал тақ тақ сан үшін N орналасады. 0, 5-тен (N + 1) дейінгі X мәніне сәйкес келеді.
Мысалы, 10 адамнан тұратын топта сырттай оқитын студенттердің жасы туралы мәліметтер бар - Х: 18, 19, 19, 20, 21, 23, 23, 25, 28, 30 жас. Бұл мәліметтер өсу ретімен реттелген және олардың саны N = 10 біркелкі, сондықтан медиан X5 = 21 мәндеріне сәйкес келетін 0. 5 * 10 = 5 және (0. 5 * 10 + 1) = 6 сандарымен Х болады. және X6 = 23, содан кейін медианасы: Мен = (21 + 23) / 2 = 22 (жыл) .
Егер Х тең аралықтар түрінде берілсе, онда медианалық интервал алдымен анықталады (жиіліктердің жартысы f аяқталады, ал екінші жартысы басталады), онда медиананың шартты мәні формула бойынша табылады:
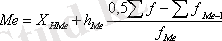
1. 3Үйлесімдік орташа шаманың ерекшеліктері
Үйлесімдік орташа - бұл арифметикалық орташа шаманың кері немесе өзгертілген түрі. Егер өзгермелі қатардың белгілері (х) оның жиілігі мәндері (f) берілген болса, онда ариыметикалық шама қолданылады, ал кейбір кезде өзгеше, өзгермелі қатардың белгілері (х) пен оның жиілігіне (xf) беріліп, жиілік мәндері (f) мәндері белгісіз болуф мүмкін.
Үйлесімдік орташа берілген мәліметтердің экономикалық маңызы мен мәнәне қарай, есептеу тәсіліне қарай жай және салмақталған болып 2 түрге бөшлінеді.
Үйлесімдік орташа - атрибут пен өнімнің жеке мәндері белгілі болған және жиіліктері белгісіз болған жағдайларда қолданылады.
Кірістілік белгілі - ауданы белгісіз (астықтың жалпы шығымдылығын өнімге бөлу арқылы есептеуге болады), астықтың жалпы түсімі белгілі.
Үйлесімдік орташа шама келесі формула бойынша анықтауға болады:
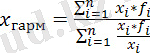
Егер көбейтіндісі бірдей болса немесе 1-ге тең болса (z = 1), есептеу үшін формула бойынша есептелген қарапайым қарапайым гармоник қолданылады:
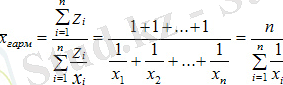
Қорытынды
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz