Электр өрісінің кернеулігі мен ағыны: Гаусстың интегралдық теоремасы және электромагниттік өріс теориясының дамуы


Мазмұны
1. Кіріспе. . 3
2. Электр өрісінің кернеулігі ағыны. Интегралдық түрдегі Гаусс теоремасы 4
3. Электромагниттік өрістер теориясының пайда болуы және дамуы . . . 7
4. Қорытынды . 11
5. Пайдаланылған әдебиеттер тізімі . 12
Кіріспе
Заманауи тұжырымдамаларға сәйкес электр зарядтары бір-біріне тікелей әсер етпейді. Әр зарядталған дене айналасындағы кеңістіктегі электр өрісін жасайды, ол басқа зарядталған денелерге күш әсер етеді.
Электр өрісінің негізгі қасиеті - бұл белгілі бір күшпен электр зарядына әсер ету. Сонымен, зарядталған денелердің өзара әрекеттесуі олардың бір-біріне тікелей әсер етуі арқылы емес, зарядталған денелерді қоршап тұрған электр өрістері арқылы жүзеге асырылады.
Электр өрісін өлшеу үшін күш сипаттамасы енгізіледі - электр өрісінің кернеуі.
Электр өрісінің кернеулігі - кеңістіктің белгілі бір нүктесінде орналастырылған оң сынақ заряды бойынша өріс әсер ететін күштің осы зарядтың мәніне қатынасына тең физикалық шама:
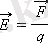
Электр өрісінің кернеулігі - вектордың физикалық шамасы. В векторының бағыты кеңістіктің әр нүктесінде оң сынақ заряды бойынша әрекет ететін күш бағытымен сәйкес келеді.
Кеңістіктегі белгілі бір нүктеде зарядтар жүйесі құрған электр өрісінің кернеуі сол зарядтар бойынша бір нүктеде құрылған электр өрісінің күштерінің векторлық қосындысына тең:
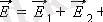
Электр өрісінің бұл қасиеті өрістің суперпозиция принципіне бағынатынын білдіреді.
Электр өрісінің кернеулігі ағыны.
Гаусс теоремасын интегралдық формада
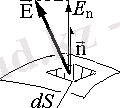 1. 1. 1-сур
1. 1. 1-сур
n - dS торабына қалыпты бірлік болсын (тораптағы E электр кернеуінің өзгеруін елемеуге шамалы) . Осы аймақ бойынша электр қарқындылығының ағынды дФе E және dS қалыпты компоненттерінің көбейтіндісі ретінде анықталады:
 (1. 1. 1)
(1. 1. 1)
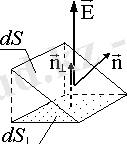
DFE ағынының белгісі қалыпты және кернеудің салыстырмалы бағытына байланысты. Егер осы екі вектор жедел бұрыш жасаса, онда ағын оң, ал егер теріс болса - теріс болады.
Өріс сызығына (мысалы, Е векторына) бейім платформа арқылы өтетін dFE ағыны осы платформаның өріс сызығына перпендикуляр жазықтыққа проекциясы арқылы өтетін ағынға тең болады (1. 1. 2-суретті қараңыз) :
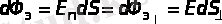 (1. 1. 2)
(1. 1. 2)
Бұл теңдік (1. 1. 1) dF e анықтамасынан және өзара перпендикуляр жағы бар бұрыштық теоремадан туындайды.
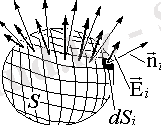 Рис. 1. 1. 3
Рис. 1. 1. 3
Тұйықталған S арқылы өтетін электрлік кернеудің Е ағыны Fe (1. 3. 3-сурет) барлық беткі аудандар арқылы өтетін элементар ағындардың сомасы ретінде анықталады. Шекте, электродтар саны шексіздікке жеткенде, электродтар арқылы өтетін ағындар жиынтығы En интенсивтіліктің қалыпты компонентінен беткі интегралға өтеді: (1. 1. 3. )
1844 жылы К. Гаусс өріс көздері мен қарқындылық ағындары арасындағы қоршаудағы ерікті бет арқылы байланыс орнататын теореманы (интегралдық түрдегі Гаусс теоремасы) дәлелдеді.
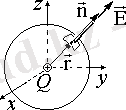 Мұны дәлелдеу үшін біз көмекші формула аламыз. Нүктелік зарядтан оның айналасындағы еркін шеңбер арқылы ағыңыз.
Мұны дәлелдеу үшін біз көмекші формула аламыз. Нүктелік зарядтан оның айналасындағы еркін шеңбер арқылы ағыңыз.
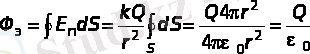 (1. 1. 4)
(1. 1. 4)
Нүктелік заряд өрісінің өріс сызықтары концентрлік сфераның бетіне перпендикуляр орналасқан (1. 1. 4-суретті қараңыз) . Осы фактіні ескере отырып, (1. 1. 4) формула нүктелік заряд өрісі өрнегінен алынған. Көріп отырғанымыздай, бұл жағдайда F e ағыны сфераның радиусына тәуелді емес, тек Q-қа тәуелді болады.
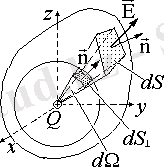
1. 1. 5-сур
(1. 1. 2) және (1. 1. 4) тармақтарынан зарядтың айналасындағы кез-келген бет арқылы нүктелік заряд өрісінің ағыны концентрлік зарядтың еркін радиусы шеңберінің ағынына тең болатындығы шығады. Шынында да dS кез-келген аудан арқылы нүктелік заряд өрісінің еркін сызықтан d angle қатты бұрышпен кесілген ағыны бірдей қатты бұрышпен кесілген сфера шеңберінің ағынымен бірдей. Фе өрісінің сфера арқылы ағуы, жоғарыда айтылғандай, оның радиусына тәуелді емес. Сондықтан S беті арқылы нүктелік зарядтың өріс күшінің ағыны (1. 3. 5 суретті қараңыз) (1. 3. 4) формуламен келтірілген. (1. 3. 4) формуласы және суперпозиция принципі Гаусс теоремасын интегралдық формада білдіреді: электр өрісінің Fe ағынының ерікті жабық бет арқылы өтетіндігі, оның ішінде еркін таратылатын зарядтары бар (көлемі, беті және т. б. ) Q, формула бойынша есептеледі.
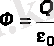 (1. 1. 5)
(1. 1. 5)
Есептерді шешуде Гаусс теоремасын қолданған кезде (1. 1. 5) Q теңдеуі ағым есептелетін ақыл-ой бетіндегі барлық зарядтардың, соның ішінде атомдар мен орта молекулаларына тиесілі зарядтардың қосындысын (байланысты заряд деп аталады) есте сақтау қажет.
Өріс күшінің Е толқындары нөлге тең болатын кез келген жабық бет арқылы ағыны да нөлге тең болады.
Электромагниттік өріс теориясының
пайда болуы және дамуы
17-18 ғасырларда электромагниттік процестер ғылымға тереңдеп, тереңдей түсті: физика мен химия. Механикалық бейненің орнына әлемнің электромагниттік бейнесінің дәуірі келді.
Максвелл оптика мен электрдің үлкен синтезін жүргізе отырып, электромагниттік заңдардың негізгі маңыздылығын анық көрді. Ол жарықтың электромагниттік теориясын құра отырып, оптиканы электромагнетизмге дейін азайтты және сол арқылы тек теориялық физикаға ғана емес, сонымен қатар технологияға, радиотехника үшін жаңа жолдар салды.
Фарадей электрлік және магниттік құбылыстарды зерттеуде жаңа тәсілді қолдана отырып, ортаның рөлін көрсетіп, өріс сызықтарын қолдана отырып, өзі сипаттаған өріс туралы түсінік енгізді. Максвелл математикалық толықтыққа идеялар берді, Фарадей әлі анықтамаған «электромагниттік өріс» терминін дәл осы өрістің математикалық заңдылықтарын тұжырымдады. Галилей мен Ньютон әлемнің механикалық бейнесінің негізін қалады, Фарадей мен Максвелл - әлемнің электромагниттік суретінің негізін қалады.
Максвелл күштердің физикалық сызықтары туралы (1861-1862) және динамикалық өрістер теориясы (1864-1865) еңбектерінде электромагниттік теорияны дамытады. Ол енді бұл шығармаларды Абердинде емес, Лондон қаласында, Кинг колледжінде профессорлыққа жазды. Мұнда Максвелл қазірдің өзінде ескі және науқасы бар Фарадеймен кездесті. Максвелл жарықтың электромагниттік сипатын растайтын мәліметтерді алып, оларды Фарадейге жіберді. Максвелл былай деп жазды: «Ол (Фарадей) ұсынған жарықтың электромагниттік теориясы« Радиациялық тербелістер туралы ойлар »(Фил. Маг., Мамыр 1846) немесе« Эксперименталды зерттеулер »(эксп., 447 б. ) . дәл осы мақалада («Динамикалық өрістердің теориясы» - Фил. Маг., 1865) дами бастадым, тек 1846 жылы таралу жылдамдығын есептеу үшін деректер болмаған. Ж. Қ. М.
1873 жылы Максвеллдің негізгі жұмысы «Электр және магнетизм туралы трактат» жарық көрді. Ол өзінің теориясы, қарапайым электр энергиясы туралы танымал экспозиция жаза бастады, бірақ оны аяқтай алмады.
Максвелл жан-жақты ғалым болды: теоретик, экспериментші және техник. Бірақ физика тарихында оның аты, ең алдымен, өзі жасаған электромагниттік өріс теориясымен байланысты, оны Максвелл теориясы немесе Максвеллдің электродинамикасы деп атайды. Ол ғылым тарихына Ньютон механикасы, релятивистік механика, кванттық механика сияқты іргелі жалпылаулармен бірге еніп, физикада жаңа кезеңнің басталуын белгіледі. Аристотель тұжырымдайтын ғылымның даму заңына сәйкес, ол табиғат туралы білімді жаңа, жоғары деңгейге көтерді және сонымен бірге Аристотель айтқандай, «бізге түсініксіз» деген алдыңғы теорияларға қарағанда түсініксіз, дерексіз болды.
Максвелл өзінің теориясын 1854 жылы дамыта бастады.
Максвелл электротониялық күйді үш функцияны қолдана отырып сипаттайды, ол оны электртониялық функцияларды немесе электротониялық күйдің компоненттерін атайды. Қазіргі таңбалауда бұл вектор функциясы потенциалды векторға сәйкес келеді. Максвелл осы вектордың жабық сызық бойындағы қисықтық сызықты интегралын «тұйықталған қисық бойындағы жалпы электротоникалық қарқындылық» деп атайды. Осы шама үшін ол электротониялық күйдің бірінші заңын табады: «Беттік элементтің шекарасы бойындағы жалпы электртоникалық қарқындылық осы элементтен өтетін магнит индукциясының шамасын немесе басқаша айтқанда, берілген элементке енетін магниттік сызықтар санын өлшеу ретінде қызмет етеді. » Қазіргі таңбада бұл заңды формула бойынша білдіруге болады:
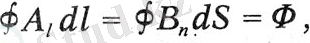
мұндағы A - dl қисығының элементі бағытындағы потенциалды вектордың компоненті, Bn - индукция векторының В бетінің элементіне қалыпты бағыттағы қалыпты компоненті.
Бұдан әрі Максвелл «магнит өткізгіштік теңдеуін» жазады:
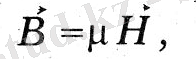
магнит индукциясын B магнит өрісінің векторымен байланыстыру.
Үшінші заң H магнит өрісін оны құратын токтың күшімен байланыстырады. Қазіргі таңбалауда бұл сөйлем формуламен сипатталады
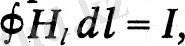
ол қазір интегралдық түрдегі алғашқы Максвелл теңдеуі деп аталады. Ол Оерстед ашқан тәжірибелік фактіні көрсетеді: ток магнит өрісімен қоршалған.
Токтардың күш әсерлесуін сипаттау үшін Максвелл магниттік потенциал деп аталатын шаманы енгізеді. Бұл шама бесінші заңға сәйкес келеді: «Тұйықталған токтың жалпы электромагниттік потенциалы токтың шамасына және тізбек бойындағы жалпы электротоникалық кернеуге көбейтілген ток бағытымен есептеледі:
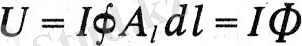
Максвеллдің алтыншы заңы электромагниттік индукцияға қатысты: «Өткізгіштің элементіне әсер ететін электр қозғаушы күш, бұл туынды электротониялық күйдің шамасы немесе бағыты өзгеруінен туындағанына қарамастан, электротоникалық қарқындылықтың уақыт туындысымен өлшенеді». Қазіргі таңбалауда бұл заң формуламен көрінеді:
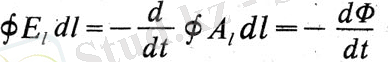
Бұл интегралдық формадағы екінші Максвелл теңдеуі. Максвелл электр өрісі векторының айналымын электр қозғаушы күш ретінде қарастыратынын ескеріңіз. Максвелл Фарадей-Ленц-Нейман индукциясының заңын жалпылайды, бұл магнит ағынының уақытының өзгеруі (электртониялық күй), бұл өріс ток өткізетін немесе өткізбейтін тұйық өткізгіштер бар-жоқтығына қарамастан бар құйынды электр өрісін тудырады деп есептейді. Максвелл әлі Оерстед заңы туралы жалпылама мәлімдеме бермейді.
Тағы бір маңызды жаңалық - бұрыс және бұрыс токтар туралы түсініктерді енгізу. Максвеллдің айтуынша, орын ауыстыру электр өрісіндегі диэлектрик күйлеріне тән. Жабық бет арқылы өтетін жылжудың жалпы ағыны бет ішіндегі зарядтардың алгебралық қосындысына тең. Бұл ағымдық жағымсыздықтың негізгі тұжырымдамасын ұсынады. Бұл ток, сондай-ақ өткізгіштік тогы магнит өрісін жасайды. Сондықтан Максвелл қазір Максвеллдің бірінші теңдеуі деп аталатын теңдеуді жалпылайды және бірінші бөлімде бұрыс токты енгізеді. Қазіргі таңбалауда бұл Максвелл теңдеуі келесі формада болады:
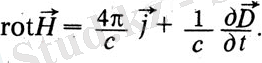
Бұдан әрі Максвелл өрісті бүкіл энергияға таралатын энергия тасымалдаушысы деп санайды. Электр өрісінің энергиясы келесі формула бойынша өрнектеледі:
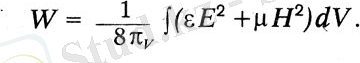
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz