Сипаттамалық теңдеудің түбірі

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 32 бет
Таңдаулыға:

Мазмұны
Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 4
1. №1дәріс ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...5
2. №2дәріс ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...9
3. №3 дәріс ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..15
4. №4 дәріс ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ...21
5. №5дәріс ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .26
6. №6дәріс ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...30
7. №7дәріс ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...34
8. №8 дәріс ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 38
9. №9 дәріс ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... 43
Әдебиеттер тізімі ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... .49

Кіріспе
Электр тізбектерінің теориясы пәні радиотехника, есептеу техникасы, байланыс мамандығының бакалаврларын дайындау үшін негізгі базалық курс болып табылады. Пәннің мақсаты - әртүрлі радиотехникалық қондырғыларда, байланыс және есептеу техникасының құрылғыларында болатын электрмагниттік процестер мен құбылыстарды зерттеу. Дәрістер жинағы үш негізгі тараудан тұрады: өтпелі процестер, сызықты емес электр тізбектері және жинақталған параметрлі тізбектер.
Бірінші тарауда өтпелі кезеңдерді шешудің классикалық, операторлық, спекторлі және Дюамель интегралы әдістері қарастырылған.
Екінші тарауда тұрақты тоқтың сызықтысыз электр тізбектері және гармоникалық әсер кезіндегі сызықсыз электр тізбектері қарастырылады.
Үшінші тарауда таратылған көрсеткіштері бар тізбектер қарастырылады.
Дәрістер жинағы 050719 - Радиотехника, электроника және телекоммуникация, 050704 - Есептеу техникасы және бағдарламаны қамтамасыз ету, 050703 - Ақпараттандыру жүйелері мамандықтарының студенттеріне арналған.

№1 дәріс. Жинақталған көрсеткішті сызықты электр тізбектеріндегі өтпелі кезеңдер
Дәрістің мақсаты: сызықты электр тізбектерін классикалық әдіспен шешуді зерттеу.
Мазмұны:
- ерікті (қалыптасқан) және еріксіз өтпелі ережелер;
- коммутация заңдары;
- біртекті дифференциалды теңдеудің ерікті құраушыларының жалпы шешімі;
- тізбектің уақыт құраушысы;
Электр тізбегі өзгеріске ұшырағанда (қосу, ажырату, қысқа тұйықталу, қандай да көрсеткіштердің тербелісі т.б) тізбекте өтпелі кезең пайда болады. Өтпелі кезең лезде ағып өте алмайды, өйткені тізбектің электрмагниттік өрісінде жинақталған энергияның лезде өзгеруі мүмкін емес. Сондықтан катушка (орам) мен конденсатордың электрмагниттік өрісінде жинақталған энергияның мәні мен жаңа күйдегі тізбектің мәні сәйкес келмейді.
Өтпелі кезең кезінде кондырғының бұзып, тіпті істен шығаратын асқын кернеу, асқын тоқ, электрмагниттік тербелістер болуы мүмкін. Сонымен бірге өптелі кезеңдер әртүрлі электронды генераторларда тиімді қолданылуда.
Классикалық әдіспен шешу
Өтпелі кезеңдерді классикалық әдіспен шешу тізбектің өтпелі кезеңі болған бөлігіндегі тоқ пен кернеудің өзгерісін сипаттайтын дифференциалды теңдеулерді интегралдауға негізделген.

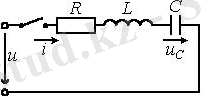
1.1 Сурет
Сызықты резистор R, индуктивтілік орамы L және сыйымдылық С құралған тізбектей қосылған тізбекке қорек көзінен U кернеу берілген (1.1 Сурет):

.
(1.1)
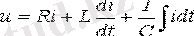Тоқтың сыйымдылық арқылы мәнін (1.1) қойып:
,
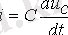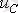қатысты екінші ретті сызықты дифференциалды теңдеу аламыз:
.
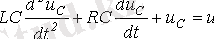Жалпы түрде n тәуелсіз жинақтауышы бар тізбектегі өтпелі кезеңнің теңдеуі:
,
(1.2)
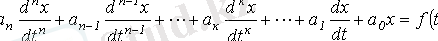мұндағы, х - ізделінген уақыт функциясы (кернеу, тоқ, ағын ілінісуі және т.б.);
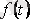- белгілі ауытқу әсері (электр энергия көзінің кернеуі немесе тоғы);
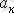- к тұрақты еселеуішті, тізбектің көрсеткіштерімен анықталады.
(1.2) теңдеуінің жалпы шешімі біртекті емес теңдеу мен біртекті теңдеудің жалпы шешімдерінің қосындысына тең болады. Ал, (1.2) 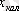дербес шешімі оң жақтағы 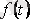функциясымен анықталады. Сондықтан еріксіз құраушы деп аталады. Тұрақты немесе периодты кернеу (тоқ) көздері берілген тізбектердегі еріксіз құраушыны анықтау үшін жоғарыда айтылған кезкелген сызықты электр тізбегін шешу әдісінің коммутациядан кейінгі сұлбасының қалыптасқан жұмыс ережесінн табу керек.
Жалпы х теңдеуінің (1.2) екінші құрушысы 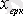((1.2) оң жақтағы шешімі) - ішкі (еріксіз) күштердің тізбекке тікелей әсер етпейтін ережесіне сәйкес келеді. Қорек көзінің әсері орама мен сыйымдылықтың өрісінде жинақталған энергияға байланысты. Сұлба жұмысының бұл ережесі ерікті, ал 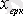- ерікті құраушы деп аталады.
Жоғарыда айтылғандарға байланысты (1.2) жалпы шешімі мына түрде болады:

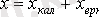
(1.3)

Бастапқы шарт. Коммутация заңдары.
Ерікті құраушысы 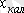анықтағанда оның мәнінде 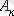интергалдау тұрақтысы болады. 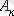-нің мәні дифференциалды теңдеудің ретіне тең. Интегралдау тұрақтысы бастапқы тәуелсіз және тәуелді шарттарға бөлу арқылы табылады.
Тәуелсіз бастапқы шарттарға уақыт моментіндегі (коммутация моменті) индуктивті орама мен сыйымдылық заряд (кернеу) үшін ағын ілінісуі (тоқ) жатады. Тәуелсіз бастапқы шарттар коммутация заңдарының негізінде анықталады.
Коммутацияның бірінші заңы - индуктивті орамалы тармақтағы коммутация кезіндегі тоқ өзінің коммутацияға дейінгі мәніне тең және әрі қарай 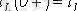өзгере бастайды.
Коммутацияның екінші заңы - сыйымдылықтағы кернеу коммутация кезінде өзінің коммутацияға дейінгі мәніне тең және әрі қарай өзгере бастайды.
Тәуелді бастапқы шарттар деп басқа тоқ пен кернеулердің мәнін айтады. Сонымен бірге коммутация кезінде тәуелсіз бастапқы шартпен ( 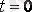үшін Кирхгоф заңымен құралатын теңдеумен) анықталатын ізделінді функцияның туындысын айтады. Бастапқы шарттың керекті мәні интегралдау тұрақтысынңың мәніне тең.

Сипаттамалық теңдеудің түбірі. Уақыт тұрақтысы.

Ерікті кұраушы 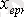мәні х дифференциалды теңдеуінің жалпы шешімінен сипаттамалық теңдеуінің түбірі арқылы анықталады

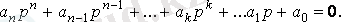
1.1 К е с т е - Жалпы шешімнің ерікті құраушыларының мәні

Сипаттамалық теңдеудің түбірінің түрі
Ерікті құраушының мәні

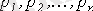
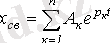
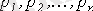және

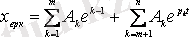
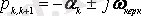
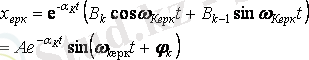
Уақыт өткеніне қарай сызықты тізбектерде ерікті құраушы өшеді, сипаттамалық теңдеудің 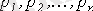түбірлері теріс болуы мүмкін.
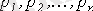түбірлерде 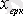монотонды өшіп, апериодты өтпелі кезең жүреді. 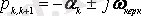түбірдің болуы өшетін синусоидалды тербелістердің (тербелмелі өтпелі кезең) пайда болуын шарттайды.
Тербелістің өшу жылдамдығы мына қатынаспен сипатталады және ол тербеліс декременті деп аталады
,
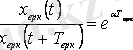немесе логарифмдік декремент деп аталатын натурал логарифмдік қатынаспен
,
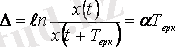мұндағы, 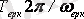, 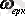- өзіндік және ерікті тербелістердің бұрыштық жиілігі.
Өтпелі кезеңдерді зерттегенде уақыт тұрақтысы маңызды сипаттама болып табылады. Ол бірінші реттік тізбек үшін анықталады
,
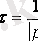мұндағы, р - сипаттамалық теңдеудің түбірі.
Уақыт тұрақтысы ерікті құраушының бастапқы мәнімен салысырғанда е есе азаю уақыт интервалында интерпретталады. Тоерия жүзінде өтпелі процесс ұзақ жүреді. Практика жүзінде 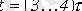уақытта бітеді деп есептейміз.

№ 2 дәріс. Сипаттамалық теңдеуді құрудың тәсілдері
Дәрістің мақсаты: сипаттамалық теңдеуді құрудың тәсілдерін үйрену және RL тізбегіндегі өтпелі кезеңдерді есептеу.
Мазмұны:
- сипаттамалық теңдеуді құрудың тәсілдері;
- RL тізбегін тұрақты кернеу көзіне қосу;
- RL тізбегін синусоидалы кернеу көзіне қосу;
- RL тзбегіндегі қысқа тұйықталу;

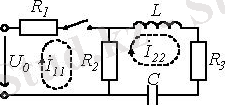
2.1 Сурет
Тізбекке сипаттамалық теңдеу коммутациядан кейін құрылады, Ол келесі тәсілдермен құрылуы мүмкін.
(1.2) кейіптеме бойынша дифференциальды теңдеу негізінде анықталады.
Бірінші тәсілде алдынғы дәрісте анықталған RLC тізбекті конденсаторда 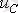қатысты дифференциальды теңдеумен анықтаймыз. Ескере кететін жайт, сызықты тізбек бірыңғай өтпелі кезеңді қамтитындықтан, сипаттамалы теңдеудің сұлба тармағының кернеуі мен тоғының барлық еркін құраушыларының жалпы түбірі болып табылады.
Сипаттамалы теңдеу құрудың екінші тәсілін келесі мысалда қарастырамыз ( 2.1 сурет).
Сипаттамалы теңдеуді кіріс кедергі әдісі бойынша құру төмендегідей жүзеге асады:
- айнымалы тоқ тізбегіндегі кіріс кедергі жазылады;
- jw - р операторымен ауыстырылады;
- табылған 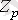өрнегі нөлге теңестіріледі.
Теңдеу сипаттамалы теңдеуге үйлесімді болады.

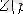
Тоқ көзінің қысқыштарына қатысты 2.1 суреттегі тізбекте

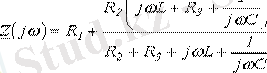
Jw-ны р операторына ауыстырып және алынған өрнекті нөлге теңестіріп мынаны жазамыз:

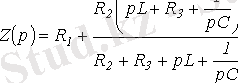
немесе

(2.1)
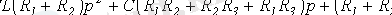
Өтпелі кезеңдерді есептеудің жалпы классикалық әдісі
Жалпы алғанда, өтпелі кезеңдерді есептеудің классикалық әдісі келесі кезеңдерден тұрады:
а) бастапқы тәуелсіз шартты анықтау -;
б) ізделінді айнымалы келесідей жазылады:

(2.2)
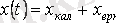
в) тізбектегі коммутациядан кейінгі қалыптасқан ережеде де есептелуге негізделген еріксіз құраушының жалпы шешімін анықтау;
г) сипаттамалы теңдеу құру және оның түбірлерін анықтау. Анықталған түбірлер типіне байланысты еркін құраушылар өрнегін жазу;
д) табылған өрнектерді сәйкесінше еріксіз және еркін құраушылар орнына қою (2.2);
е) бастапқы шартты анықтау және оның негізінде интегралдау тұрақтысын табу.
Өтпелі кезеңді классикалық әдіспен есептеуге мысалдар

Кернеу көзіне қосылған RL тізбегіндегі өтпелі кезең.

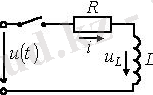
2.2 Сурет
Екі жағдайды қарастырамыз:
а)
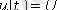
б) .
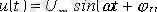Қаралған әдіске сәйкес тәуелсіз бастапқы шартты қарастырамыз 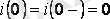, 2.2 суреттегі тізбектің тоғы үшін:

(2.3)
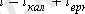
Онда бірінші жағдай үшін тоқтың еріксіз құраушысы

(2.4)
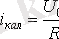
Сипаттамалық теңдеу

,
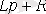Одан 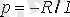және уақыт тұрақтысы .
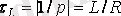Осыдан,

(2.5)
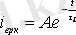
(2.4) және (2.5) өрнектерін (2.3) қойып мынаны жазамыз,
.
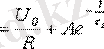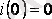болғандықтан,

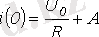
аламыз.

мұндағы,

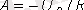
2.3 Сурет
.
Бұдан өтпелі кезеңдегі тізбек тоғы:
,
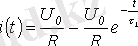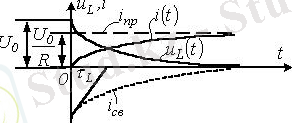
Ал индуктивтіліктегі кернеу:
.
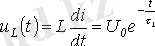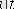және 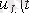қисықтары 2.3 суретте көрсетілген.
Қорек көзінің екінші түрінде еріксіз құраушыларды комплекстік әдіспен есептейміз.
,
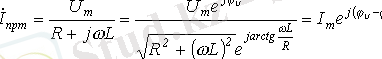мұндағы, .
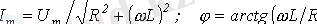Осыдан
.
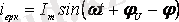Еркін құраушының өрнегі кернеу көзінің түрінен тәуелді емес. Ендеше:
.
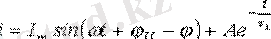болғандықтан,
.
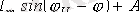Сондықтан да , нақтылай қорытынды аламыз.
.
(2.6)
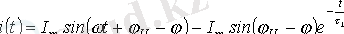Алынған (2.6) теңдеудің талдануы:
а) бастапқы фаза кернеуінде интегралдау тұрақтысы А=0. Сондықтан, осы жағдайды коммутация артынан өтпелі кезеңде жетектемейді. Тізбекте орнатылған ереже туады;
б) 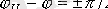болғанда еркін құраушы модульге максималды. Өтпелі кезеңдегі тоқ өзінің ең үлкен шамасына жетеді.

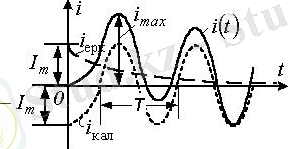
2.4 Сурет
Егер 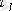шамаға мәнді болса, жарты периодтық еркін құраушы маңызды кемімейді. Осы жағдайда өтпелі кезеңдегі 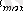максималды тоқ шамас, амплитудалық тоқтың орнатылған ережесінен асуы мүмкін. 2.4 суретінде көрсетілгендей, мұнда 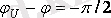, тоқ максимумы 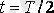кейін орын алады. 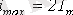аралық негізінде.
Сондықтан сызықты тізбек үшін максималды мәнінің тоғы өтпелі ережедегі екі еселенген амплитуданың еріксіз тоғынан 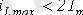аспайды.
Конденсатормен сызықты тізбек үшін іспеттес: егер коммутация кезінде еріксіз (қалыптасқан) кернеу өзінің мәніне тең болса және уақыт тұрақтысы жеткілікті үлкен болса, ендеше жарты периодты кернеуінен кейін конденсатор өзінің 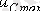максималды мәніне жетеді, онда ол екі еселенген амплитудалық еріксіз кернеуден 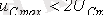аспайды.Индуктивті ораманы қорек көзінен ажыратқандағы өтпелі кезең. Кілттің тізбекте ажырауында (2.5 сурет) еріксіз тоқтың құраушысы индуктивті орамасынан 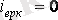өтеді

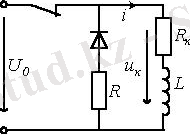
2.5 Сурет
Сипаттамалық теңдеуі
,
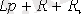осыдан 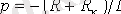және .
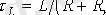Коммутацияның бірінші заңына сәйкес
.
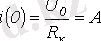Сондықтан да, өтпелі кезеңдегі тоқ үшін

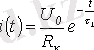
және индуктивті орамадағы кернеу

(2.7

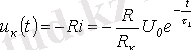
№3 дәріс. Конденсатордың заряды және разряды

Дәрістің мақсаты: классикалық әдіспен RC және RLC- тізбегінің өтпелі кезеңін есептеу және талдауын алу.
Мазмұны: - RC тізбегіндегі өтпелі кезеңдер;
- RLC - тізбегін тұрақты кернеу көзіне қосу;
Кілтті бір түрге ауыстырғанда конденсатордың зарядталу кезеңі басталады.

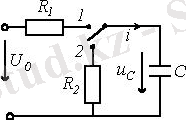
3.1 Сурет

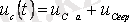
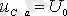конденсатордағы еріксіз (қалыптасқан) құраушы кернеу.
Сипаттамалық теңдеуден

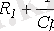
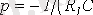- түбірін анықтаймыз. Осы жерден уақыт тұрақтысы. .
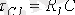Осыдан,
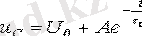. (3.1)
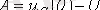t=0 болғанда конденсатор кернеуі - ға тең (жалпы жағдайда коммутация кезінде конденсатор зарядталған болуы мүмкін). Сондықтан және
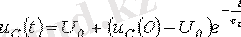. (3.2)
Зарядталған тоққа қатысты былай жазуға болады.
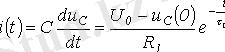. (3.3)
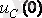шамасына байланысты:
1. -;
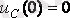2. -;
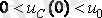3. -;
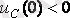4. - 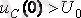- осыдан төрт қисық өтпелі кезең болуы мүмкін, 3.2 суретте көрсетілген.

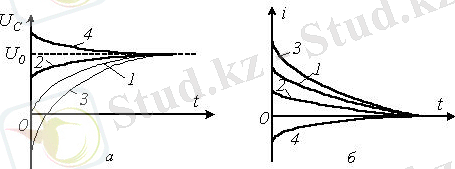
3.2 Сурет
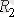резисторында конденсатор разрядталса (3.1 суретіндегі кілт 2 түрге ауыстырылады) 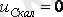. Уақыт тұрақтысы .
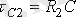Коммутация кезінде конденсатор 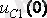кернеуінде зарядталған болса (кейбір кезде 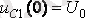), өтпелі ережеде кернеуді былай жазуға болады.
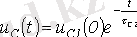. (3.4)
Сәйкесінше разрядты тоқ
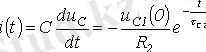(3.5)

Өтпелі кезеңде RLC- тізбегін кернеу көзіне тізбектей қосылған.
Мына жағдайды қарастырайық.

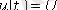
Алдыңғы дәрісте қарастырғандай өтпелі кезеңдегі классикалық әдісті конденсатордағы кернеуді 3.3 суретіндегі тізбекке қарап былай жазуға болады.

(3.7)

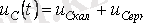
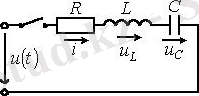
3.3 Сурет
Бірінші жағдай үшін мына кернеудің еріксіз құраушысы
.
((3.8)
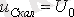Тізбектің сипаттамалық теңдеуі
,
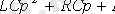Осыны шешіп, келесіні аламыз
.
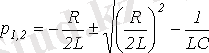Тізбек көрсеткіштерінің арақатынасына байланысты үш түбір болуы мүмкін және еркін құрастырушылар үшін үш нұсқа қарастырамыз:
1. 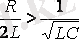немесе 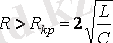, мұндағы 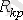- контурдың критикалық кедергісі, еркін кезең кіші тербелмелі сипаттамасын бірге алып жүреді.
Осыдан

((3.9)
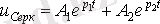
2. 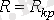- периодикалық емес ереженің шегі.
Осы жағдайда 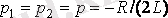және

(3.10)
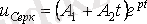
3. 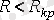- өтпелі кезеңнің периодикалық (тербелмелі) сипаттамасы.
Осы жағдайда 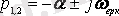және
,
(3.11)
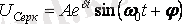мұндағы 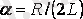- өшу еселеуіші;
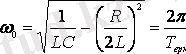- өзінің немесе еркін тербелістің бұрыштық жиілігі;
- өздік тербелістің периоды.
Өтпелі кезеңнің периодикалық емес сипаттамасы үшін мынаны жазуға болады:
.
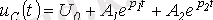Интегралдау тұрақтысын табу үшін, жалпы жағдайда 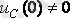және коммутацияның бірінші заңына қатысты 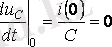, t=0 үшін екі теңдеу жазамыз.

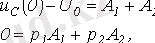
Осыны шешіп, келесіні аламыз
; .
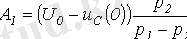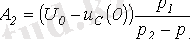Сондықтан,
.
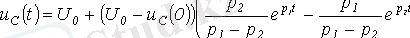Сонда тізбектің тоғы

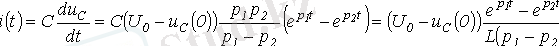
орамадағы индуктивті кернеу
.
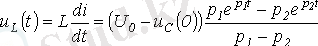3.4 суретінд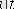е , және 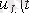сапалы кедергілер берілген, периодикалық емес өтпелі кезеңге қатысты.

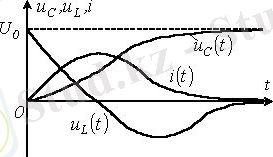
3.4 Сурет
Критикалық ереже үшін, былай жазуға болады.
.
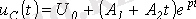болағанда

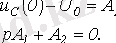
Сондықтан,
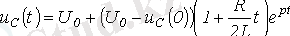және
.
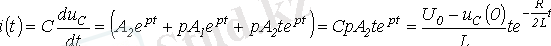Тербелмелі өтпелі ереже үшін
.
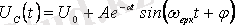Интегралдау тұрақтысын табу үшін

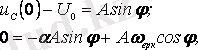
Осыдан
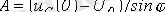және .
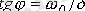сонда
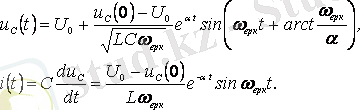
3.5 суретте 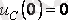кезінде тербелмелі өту кезеңіне сәйкес сапалы қисықтар Uc(t) және i(t)көрсетілген

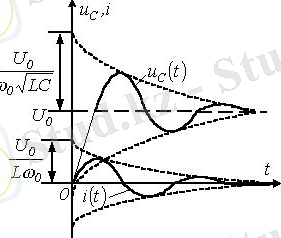
3.5 Сурет

№4 дәріс. Өтпелі кезеңдері есептеудің операторлық әдісі
Дәрістің мақсаты: операторлық әдіспен өту кезеңін есептеуді қарастыру.
Мазмұны:
- Лапластың тікелей түрленуі;
- индуктивтік және сыйымдылық элементтеріндегі кернеудің бейнесі;
- операторлық әдістегі Ом заңы;
- орынбасудың операторлық сұлбасы;
- операторлық формадағы Кирхгоф заңдары;
- бейнеден түп нұсқаға өту.
Операторлық әдістің негізі түп нұсқалы 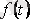функциясы бейне деп аталатын 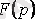кешеннің өзгерісіне 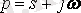сәйкестенеді. Соның нәтижесінде бейнелерге сәйкес туынды мен интеграл түп нұсқаларынан алгебралық функциялармен ауыстырылады (дифференциялды р операторға көбейтумен, ал интегралдау оған бөлумен ауыстырылады). Ол ізделінді айнымалылар бейнелеріне қатысты интегродифференциалдық теңдеулерде алгебралық теңдеулер жүйесіне өтуін анықтайды.
Теңдеулерді шешу нәтижесінде көріністер, ал кері өту кезінде түп нұсқалар жатады. Сонымен қатар басты мезеті, классикалық әдіске қарағанда жоғарғы тізбектердегі кезеңдерді есептеуді жеңілдететін бастапқы тәуелсіз шарттарын анықтау болды.
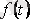функциясында берілген 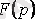Лапластың тікелей түрленуімен анықталады.

(4.1)
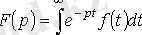
Қысқартылуы бойынша бейне мен түп нұсқаның арасындағы сәйкестік:

немесе
.
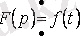
Интеграл мен туындының бейнелері
Математика курсынан 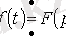болса, онда 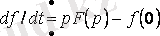, мұнда 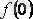- 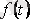функцияның бастапқы мәні.
Осылай индуктивтік элементтегі кернеу үшін

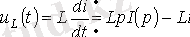
немесе бастапқы нөлдік шарттары үшін

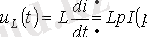
Бұдан индуктивтік катушканың операторлық кедергісі
.
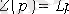Интеграл үшін: егер 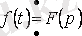, онда .
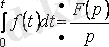Конденсатордағы бастапқы нөлдік емес шарты бар кернеуге:

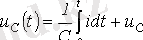
Сонда

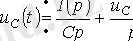
немесе бастапқы нөлдік шарттары үшін

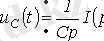
мұнда конденсатордың операторлық кедергісі

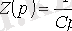
Операторлық түрдегі Ом заңы
Күрделі тізбекте белгіленген (4.1 сурет) тармағын аламыз.

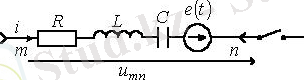
4.1 Сурет
Сыртқы тізбектегі кілттің тұйықталуы өту кезеңіне алып келеді, сонымен қатар тармақтағы тоқ және конденсатордағы кернеудің бастапқы шарттары жалпы жағдайда нөлдік емес.
Айнымалының лездік мәндері үшін

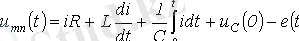
Онда жоғарыда келтірілген сәйкестіктерден:

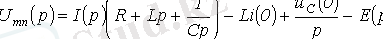
Осыдан

(4.2)
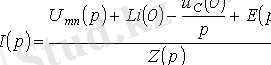
мұндағы, 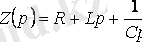- қарастырылып отырған тізбектің операторлық кедергісі.
Р операторын 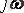ауыстыру кезінде тізбектегі синусойдалды тоқтың операторлық кедергісі 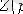комплексті кедергіге 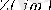сәйкес.
(4.2) теңдеу. Операторлық түрдегі ЭҚК көзі үшін Ом заңының математикалық жазылуы бар. Сонымен байланысты 4.2 суретте көрсетілген операторлық орынбасу сұлбасын 4.1 суреттегі тармақ үшін салуға болады.

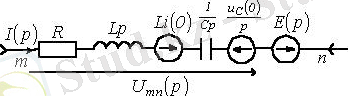
4.2 Сурет
Операторлық түрдегі Кирхгоф заңдары
Кирхгофтың бірінші заңы: түйіндес токтардың алгебралық қосындысы нөлге тең:

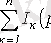
Кирхгофтың екінші заңы: контурға әсер етуші ЭҚК-ң алгебралық қосындысы осы контурдағы пассивті элементтердің алгебралық қосындысына тең.

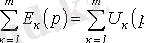
Кирхгофтың екінші заңы бойынша теңдеуді жазу кезінде нөлдік емес бастапқы шарттардағы ескеруді ұмытпау керек. Ескеру нәтижесінде соңғы сәйкестік кері түрде жазылуы мүмкін
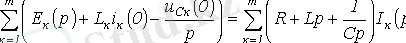(4.3)
Бейнеден түп нұсқаға өту
Ізделінді шаманың бейнесінен түп нұсқаға өту келесі әдістермен орындалуы мүмкін:
а) Лапластың кері түрленуі нәтижесінде

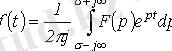
(4.1) интегралдық теңдеулерді шешумен қатар былайша қысқаша жазылады
.
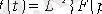Практикада бұл әдіс көп кездеспейді;
б) кестелер бойынша түп нұсқалар мен бейнелердің арасындағы сәйкестік;
Электротехниканың барлық тапсырмаларын қамтитын, жеткілікті шамадағы сәйкестік кейіптемелер арнайы әдебиеттерде кездеседі. Берілген әдіспен, кестеге сәйкес ізделінді шаманың бейнесін алып, кестеден түп нұсқаның мәнін жазып алу керек;
в) жіктеу кейіптемесін қолдану арқылы;
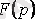ізделінді шаманың бейнесі екі полиномның қатынасымен анықталады.
,
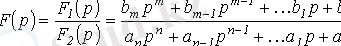мұндағы .
Сонда

(4.4)
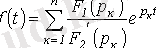
(4.4) қатынас жіктеу кейіптемесін көрсетеді.
Егер 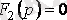теңдеуінің бір түбірі нөлге тең болса, онда 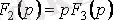, демек (4.4) теңдеуден
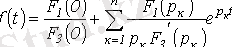(4.5)
Кешенді-түйіндес түбірлері 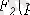болатын, қосу кезінде екі еселенген мүше беретін, кешендіі-түйіндес қосуларға жіктелу кейіптемелеріне сәйкес келеді. Демек әрбір кешенді-түйіндесу түбірлері:
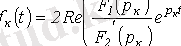(4.6)
Операторлық әдіспен өту кезеңдерін есептеу:
а) тізбектің коммутацияға дейінгі ережесі бойынша тәуелсіз бастапқы шарттарын анықтау;
б) тізбекті алмастырудағы операторлық сұлбаны құру;
в) бастапқы шарттарын ескере отырып операторлық түрдегі теңдеулерді Кирхгоф заңдары бойынша немесе сызықтық тізбектерді есептеудің басқа әдістерімен жазу;
г) алынған теңдеулердің шешімі ізделінді шамаға қатысты;
д) табылған бейнелер бойынша түп нұсқаларды анықтау.

№5 дәріс. Өтпелі өткізгіш

Дәрістің мақсаты: Дюамель интегралын немесе айнымалы қалып тәсілін қолданумен өтпелі кезеңдерді есептеуге дағдылану.

Мазмұны:
- тізбектің өтпелі функциясы;
- Дюамель интегралын қолданумен өтпелі кезеңдерді есептеу;
- қалыптың айнымалылары тәсілі;

Беттесу әдісін қарастырғанда сұлбаның әрбір тармағындағы тоқ мынадай түрде мүмкін екені көрсетілген

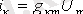
мұндағы 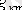- өздік (к=m) немесе өзара 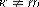өткізгіштік.
Бұл, мына теңдікке ауыстырылған ара қатынас
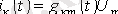(5.1)
өтпелі режимде де күшті болады, яғни m тармағындағы кілт тұйықталуы бұл тармақтығы 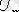тұрақты кернеу көзін тізбекке қосады. Бұл кезде 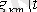уақыт функциясы болады және өтпелі өткізгіштік деп аталады.
(5.1)- не сәйкес өтпелі өткізгіштік сандық жағынан тізбекті тұрақты 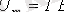кернеуіне қосқандағы тізбектегі тоққа тең.
Кернеу бойынша өтпелі функция
Кернеу бойынша өтпелі функция төртұштықтарды талдағанда жиі қолданылады.
Егер нөлдік бастапқы шарттары бар сызықты электр тізбекті тұрақты кернеу көзіне қосса, онда тізбектің m және n ерікті нүктелері арасында мына кернеу пайда болады
,
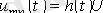мұндағы, 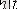- кернеу бойынша өтпелі функция, сандық жағынан сұлбаның, m және n ерікті нүктелері арасындағы, оның кірісіне 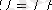тұрақты кернеуін бергендегі кернеуіне тең.
Дюамель интегралын қолданумен өтпелі кезеңдерді есептеу
Жекелік қоздыратын әсерге тізбектің реакциясын, яғни 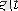өтпелі өткізгіштіктің функциясын және ( немесе ) 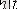кернеу бойынша өткізгіштік функцияны біле отырып, тізбектің ерікті формадағы әсерге реакциясын табуға болады. Дюамель интегралы көмегімен есептеу әдісі негізінде беттесу принципы жатыр.
Интеграциялау жүргізілетін айнымалыны және тізбектегі тоқ анықталатын уақыт мезетін анықтайтын айнымалыны бөлу үшін Дюамель интегралын қолданғанда, біріншісін , ал екіншісін - t түрінде белгілейді.

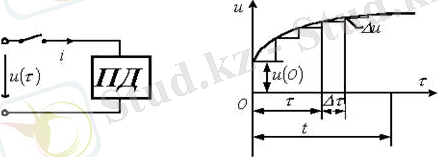
5.1 Сурет 5.2 Сурет
уақыты мезетінде нөлдік бастапқы шарттары бар тізбекке (5.1 суреттегі пассивті екіұштыққа ПЕ) ерікті формадағы 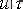кернеуі бар қорек көзі қосылады. Тізбектегі тоғын табу үшін бастапқы қисықты баспалдақтымен ауыстырайық (5.2 сурет), одан кейін тізбектің сызықты екенін ескере отырып, кернеуінің бастапқы секірісінен бастап және t мезетіне дейінгі уақыт бойынша кешігіп іске асатын кернеудің барлық баспалдақтарына дейінгі тоқтарды қосамыз.
t уақыт мезетінде кернеуінің бастапқы секірісімен анықталатын ортақ тоқтың құраушысы 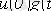тең.
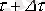уақыт мезетінде, уақыт интервалын есепке алғандағы секіріс басынан керекті t уақыт мезетіне дейінгі тоқ құраушысын шарттастыратын 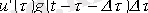, 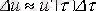кернеудің секірісі орын алады.
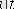толық тоғы t уақыт мезетінде 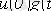ескергендегі кернеудің бөлек секірістерінен тоқтың барлық құраушыларының қосындысына тең, яғни

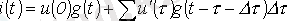
уақыт өсімінің соңғы интервалын шексіз азға ауыстырып, яғни қосындыдан интегралға көшіп мынаны жазамыз

(5.1)
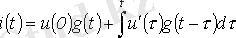
(5.1) ара қатынасы Дюамель интегралы деп аталады.

Дюамель интегралын қолданып кернеуді де анықтауға болатынын атап өту керек. Бұл кезде (5.1) - ге 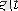өтпелі өткізгіштігінің орнына кернеу бойынша өтпелі функция кіреді.

Дюамель интегралын қолданғандағы есептеудің тізбегі:
а) қарастырылатын тізбек үшін 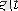(немесе 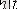) функциясын анықтау;
б) 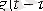(немесе 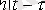) өрнегін t - ны - ға формальды ауыстыру жолымен жазу;
в) туындысын анықтау;
г) табылған функцияларды (5.1)-ге қою және белгілі бір интегралды интегралдау;

Қалыптың айнымалылары тәсілі
Қалыптың айнымалылары тәсілі, туындыларға қатысты шешіліп қойылған, яғни есептеуші техниканың құралдарымен іске асырылатын, интеграциялаудың сандық тәсілдерін қолдануға әлде қайда қолайлы болатын, бірінші ретті дифференциалды теңдеулер жүйесінің шешілуі мен ретті құрастырылуына негізделген.
Қалыптың айнымалылары мөлшері, демек қалыптың теңдеулерінің саны, энергияның тәуелсіз жинақтаушыларының санына тең.
Қалыптың теңдеулеріне екі негізгі талап қойылады:
- теңдеулер тәуелсіздігі;
- әрбір басқа айнымалылардың, қалыптың айнымалылары (қалыптың теңдеулеріне қатысты жазылған айнымалылары) негізінде қайта қалыптасуына мүмкіндік;
Бірінші талап, келесі көрсетілген қалыптың теңдеулерін құрастырудың арнайы методикасымен қанағаттандырылады.
Екінші талапты орындау үшін қалыптың айнымалылары ретінде ағын- ұстасуды (индуктивті элементтері бар тармақтардағы тоқты) және конденсаторлардағы зарядты ( кернеуді) қабылдау қажет. Шынында да, бұл айнымалылардың уақыт мөлшеріндегі өзгеру заңын біле отырып, оларды әр уақытта ЭҚК және табылған сипаттамалары бар тоқтардың қорек көзімен алмастыруға ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.