Сызықты емес теңдеулерді шешудің сандық әдістері: түбірді оқшаулаудан жақындауға дейін


Қазақстан Республикасының білім және ғылым министрлігі
Е. А. Бөкетов атындағы Қарағанды мемлекеттік университеті
Математика және ақпараттық технологиялар факультеті
«Математикадан сыныптан тыс жұмыс ( факультативтік сабақ ) » пәні бойынша
КУРСТЫҚ ЖҰМЫС
тақырыбы: « Сызықты емес теңдеулер шешімін табу үшін қолданылатын жасанды әдістер »
Орындаған:
баға күні М-301 тобының студенті
Исахан Ж. Б
Комиссия мүшелері: Жетекшісі:
1 МжИОӘ кафедрасының
2 доцент, ф. -м. ғ. к
3 Ахманова Д. М
МАЗМҰНЫ
Кіріспе . . . 3
Сызықты емес теңдеулерді шешу . . . 5
1. Алгебралық және трансценденттік теңдеулерді шешу . . . 5
2. Теңдік түбірін анықтау әдістер . …. . 8
2. 1 Жартыға бөлу әдісі . . . 8
2. 2 Кесіндіні қақ бөлу - дихотомия әдісі . . . 9
2. 3 Хордалар әдісі . . . 12
2. 4 Қию әдісі . . . 14
2. 5 Ньютон әдісі . . . 16
2. 6 Жай итерация әдісі . . . 192. 7 Зейдел әдісі . . . 21
3 Сызықты емес теңдеулерді шешу кезеңдері . . . 23
3. 1 Түбір жатқан аралықты анықтау әдісі . . . 23Қорытынды . . . 25
Пайдаланған әдебиеттер тізімі . . . 26
Сабақтың барысы . . . 27
Кіріспе
Курстық жұмыс сызықты емес теңдеулердің түрлерін шешу жолдарын, кезеңдерің және де әдістері қарапалып, зеріттеліп мысалдар келтірілді.
Математика - нақты әлемнің сандық қатынастары мен кеңістіктік формалары туралы ғылым.
Таза математика нақты әлемнің кеңістіктік формалары мен сандық қарым-қатынасына ие, өте нақты материал болды. Бұл материал өте абстрактілі форманы қабылдайды деген факт, оның сыртқы әлемнен шығу тегі нашар өшуі мүмкін. Бірақ таза түрде осы нысандар мен қарым-қатынастарды зерттеуге қабілетті болу үшін, олардың мазмұнынан оларды мүлдем бөліп алу қажет, бұл соңғы нәрсе ретінде шетте қалдыру.
Математика қосымшалары әртүрлі. Математикалық әдісті қолдану аясы мүлдем шектелмеген: материя қозғалысының барлық түрлері математикалық тұрғыдан зерттелуі мүмкін.
Ғылым мен техниканың түрлі салаларында құбылыстар мен үдерістерді процестерді математикалық модельдеулер - жаңа білім мен технологиялық шешімдерді алудың негізгі тәсілдерінің бірі болып табылады. Оқу құралында физикалық және техникалық мәселелерді зерттеу кезінде туындайтын кең ауқымды математикалық есептерді шығарудың сандық әдістері баяндалады.
Негізгі әдістер толығымен түсінікті болу мақсатында сандық қосымшалармен келтірілген - есептеу сызбалары мен тақырыпты толығымен қамтитын сандық мысалдар келтірілген. Баяндалған әдістер ЭЕМ-да, сондайақ қарапайым жолмен есептеулер жүргізуге пайдаланылады
Курстық жұмыстың мақсаты - сызықты емес теңдеулердің шешу әдістерін және олардың шешу жолдарын жіктеу.
Курстық жұмысты орындау барысында орындалатын міндеттер:
- берілген тақырып бойынша әдебиетті үйрену;
- сызықты емес теңдеулер туралы түсінік қалыптастыру;
- әдістерді іріктеу;
- теореманы талдау;
- олардың шешу жолдарын сараптау;
Курстық жұмыс кіріспе, үш негізгі бөлім, қорытынды және
пайдаланылған әдебиеттер тізімінен тұрады.
СЫЗЫҚТЫ ЕМЕС ТУҢДЕУЛЕРДІ ШЕШУ
- Алгебралық және трансценденттік теңдеулерді шешу
f ( x ) функцияны қарастырайық.
f ( x ) = 0шартты қанағаттандыратын кез келген сан ζ функцияның нөлі
деп, немесе (1) теңдеудің шешімі деп аталады:
f ( x ) = 0. (1)
«бір өлшемді сызықты емес теңдеулер» болып табылады. Физикалық және басқада құбылыстардың теңдеумен сипатталатыны белгілі. Сол теңдеуді классикалық математикалық формуламен шешу мүмкін емес жағдайлар бар. Бұл уақытта практикада сандық әдістерге жататын әдістермен шешілетінін дәлелдеу керек. Әрине ең алдымен құрылған теңдеудің қай аралықта анықталғандығын, үзіліссіздігін, түбірінің барлығын, оның жалғыздығын дәлелдейтін аргументтерді бақылау керек. Осы этаптан өткеннен кейін ғана есепті осы теңдеуге қолдануға келетін алгоритм көмегімен шығаруға болады.
Сызықты емес теңдеулердің алгебралық және транцендентті түрі бар.
Алгебралық теңдеулер деп алгебралық көпмүшеліктерден тұратын теңдеулерді айтады. Олардың шешімдері көбіне нақты сан болады. Трансцендентті теңдеу деп құрамында тригонометриялық немесе арнаулы функциялар бар теңдеуді айтады.
Көптеген ғылыми және инженерлік есептерде, мысалы, электродинамикада берілу сызықтары мен резонаторлардағы электромагнитті толқындық тербеліс үдерістерін математикалық модельдеуде дисперсиялық деп аталатын теңдеу алады, мына түрдегі теңдеуді шешу керек болады:
f ( x ) = 0 . (1)
мұндағы f ( x ) функциясы (a, b ) интервалында анықталған және үздіксіз. f ( x )
функциясын нөлге айналдыратын x*барлық мәні, яғни f (x*) = 0, теңдеудің түбірі, ал табу үдерісі - теңдеуді шешу деп аталады (1) .
Егер (x ) функциясы x- ке қатысты көпмүше болса, онда (1) теңдеуі алгебралық сызықты емес деп аталады (мысалы, х 5 - 3х-1=0 ), егер f(x) функциясы элементар (тригонометриялық, логарифмдік, көрсеткіштік және т. б. ) функцияларынан тұрса трансцендентті деп аталады (мысалы, 2 sin ²x+3х 3 -7) . Есептеу математикасы тұрғысынан алғанда бұл функциялар эквивалентті.
(1) теңдеуін геометриялық шешу y =f (x ) функциясы графигінің ОХ осімен қиылысу нүктелерін табу болып табылады. Сызықты емес теңдеулерді шығару әдістері тура және итерациялы бөліп бөлінеді. Тура әдіс сызықты емес теңдеулерді формула көмегімен және 13 әрдайым дәл шешім шығарады (мысалы, квадрат теңдеуді шешуге арналған теңдеу) . Бірақ олар кейбір теңдеулер үшін ғана, сондықтан практикада екінші әдіс - итерациялық әдіс кеңінен қолданылады. Мұнда шығару жолы түрінде кейбір алгоритмдерді бірнеше рет қолданады. Алынған нәтиже нақты мәніне қаншалықты жақын болса да әрқашан жуықталған түрде болады. Сонымен қатар, теңдеулер көбінесе жуықталып берілген коэффициенттерден тұрады, осыдан есептің өзі түбірді нақты анықтау мағынасынан айырылады.
Итерациялық әдістерді екіге бөлуге болады:
1) Түбірі бар интервалды тарылту әдісі (мысалы, жартылай бөлу әдісі, алтын қимасының әдісі) . Мұнда y= f (x ) функциясының мәні емес, таңбасы ғана пайдаланылады. Мәндер салыстырмалы түрде қарапайым болғанымен ұқсастық жылдамдығы төмен болады.
2) y= f (x ) функциясы қандай да бір қарапайым f(x) =0 функциясына ауыстырылатын, сол үшін түбір ізделінетін аппроксимация әдістері (мысалы, хордалар әдісі, Ньютон әдісі) . y= f (x ) функциясының мәндерін пайдаланады. Бұларда ұқсастық жылдамдығы үлкенірек болады.
Жалпы жағдайда екі кезеңмен шығарылады:
1) түбірді бөлектеу, яғни (1) теңдеуінің оқшауланған түбірі бар аз ара қашықтық орнату (a, b) ;
2) итерациялық әдістің көмегімен тапсырылған дәлдік дәрежеге дейін түбірді анықтау.
Түбірді бөлектеу үшін мына теореманы қолдануға болады: Егер ара қашықтықта y= f ( x ) функциясы үздіксіз болса және f (a) мен f(b) қарама-қарсы таңбалы болса, яғни f(a) f(b) <0, онда f(x) (a, b) ара қашықтығында кем дегенде бір ақиқаттық түбірге ие болады. Осылай бола тұра егер f(x) таңба өзгертпейтін бірінші туындысы болса, онда түбір жалғыз болады.
Төмендегі теңдеуді шешу үшін мысалқарастырайық:
2 sin ²x+3х 3 - 7 = 0
х аргументіне әртүрлі мән бере отырып, функция мәнін табамыз:
f(x) = 2 sin ²x+3х 3 - 7 = 0
Мысалы, x = 0 болғанда f(x) = -7, x = 1, болғанда f(x) < 0, x = 2, болғанда f(2) > 0 . Осыдан [1, 2 ] аралығында берілген теңдеудің шешімі бар екендігі көрінеді. Бұл шешудің жалғыздығын дәлелдеу үшін берілген аралықта f(x) функциясының бірсарындылығын тексеру қажет, ол осы жерде бірсарынды өсетін функция болуы керек, яғни функцияның бірінші туындысы оң болуы қажет f(x) > 0 . Бұған көз жеткізу үшін оның бірінші туындысын табамыз f(x) = 2sin2x + 9x 3 , мұнда да функцияның [1, 2 ] аралықта тек оң мәндер қабылдайтынын оңай көрсетуге болады. Сонымен, берілген аралықта (1) теңдеуінің түбірінің жалғыз болу шарттарының екеуі де орындалады екен.
Екінші кезеңде түбірді анықтау итерациялық әдістердің бірінің көмегімен іске асырылады, яғни {x k }k =0, 1, … шешуге жақындау тізбегі құрылады және мұнда итерациялық үдерістің екі өлшемдерінің бірін қолдануға болады:
1) f(x k ) < e ,
2) x k -x k-1 < e .
Екеуін бірге қолдануға да болады.
Итерациялық әдістердің негізгі сипаттамасы болып, олардың ұқсастық жылдамдығын сипаттайтын реті, яғни тапсырылған дәлдік болатын итерациялар саны табылады. Келесі жуықтау мен дәл шешудің арасындағы ара қашықтықты e k = x k - x* арқылы белгілейміз. Көріп отырғандай, әдіс ұқсастығы үшін шамасы -дан кем болуы керек, яғни ⁄ қатынасы бірден кем болуы керек. Бұл қатынас неғұрлым азырақ болса, ұқсастық жылдамдығы соғұрлым көбірек болады.
Сызықты емес алгебралық және трансценденттік теңдеулер жүйесі үшін түбірді қандайда бір жолмен бөліп алуға болмайды. Кейбір жағдайларда берілген функциялардың кестелерін немесе сызбаларын құрастырып, қиылысу нүктелері координаттарын анықтау нәтижесінде түбірдің жуықталған мәнін алуға болады. Көбінесе іс жүзінде осы топтаманың алдыңғы жүйесін шешу келесі жүйені шешуге жақсы бастапқы жуықтау болатындықтан жүйенің топтамасын шешкенде түбірді бөлектеу қиындығы оңай шешіледі.
Сызықты емес алгебралық және трансценденттік теңдеулер жүйесінің түбірлерін анықтау үшін тура әдістер емес, тек итерациялық әдістер ғана қолданылады. Көбінесе сызықты емес алгебралық және трансценденттік теңдеулер жүйесін шешу үшін Ньютон әдісі мен оның түрлендірулері қолданылады.
2. Теңдік түбірін анықтау әдістерСызықты емес теңдеуді сандық шешу екі тәсілден тұрады.
- Тура тәсіл - есепті математикалық дәлелденген бір формулаға қою арқылы тікелей шығару;
- Итерациялық тәсіл - есепті формула көмегімен бастапқы жуықтауды беру арқылы жуықтап, біртіндеп шығару;
Тура тәсілмен шығарылған есептер дәл мәнді береді. Ал итерациялық тәсілмен шешілген есептер есептің жуық мәнін береді. Мұның ішінде итерациялық әдістер сандық әдіске жатады.
Бір өлшемді сызықты емес теңдеуді шешудің келесі әдістері бар.
- Кесіндіні қақ бөлу - дихотомия әдісі деп аталады;
- Хорда әдісі;
- Жанама әдісі немесе Ньютон әдісі;
- Қарапайым итерациялық әдіс немесе жәй итерация әдісі т. б. ;
2. 1 Жартыға бөлу әдісі
Итерациялық үдерістің баяу ұқсастығынан орындалатын жұмыс көлемі дәлдік өскен сайын артатындығынан жартыға бөлу әдісі сенімді және оны теңдеудің түбірін табуға өте қолайлы. Егер f(x) мына [a, b] және f(a) f(b) < 0 аралықта үздіксіз болса, осы әдіс қолданылады.
Бұл әдістің мәні мынада (2. 1-суретті қараңыз) . Мысалы, (1) теңдеуінің түбірі бөлінді делік, яғни жалғыз түбірден тұратын [a, b] арасы табылды делік. Енді тапсырылған e дәлдікпен оның жуықталған мәнін табу керек. Түбірді есептеу алгоритмі мынадай болады:
а) [a, b] арасының ортасы анықталады: c=(a+b) /2;
б) f(x) шартының орындалуы тексеріледі, егер бұл шарт орындалса, онда ізделініп отырған шама табылып, с мәні шығарылады;
в) егер f(c) = 0 шарты орындалмаса, мына шарт тексеріледі
f(c) f(a) < 0;
егер бұл шарт орындалса, онда b=c, керісінше болса a=c;
г) a - b <eшарты тексеріледі, егер бұл шарт орындалса теңдеуді шығару үдерісі аяқталып, ізделініп отырған шаманың мәні шығарылады егер бұл шарт орындалмаса, яғни тапсырылған дәлдік шықпаса, онда а) бөліміне оралып, есептеуді жалғастырамыз.
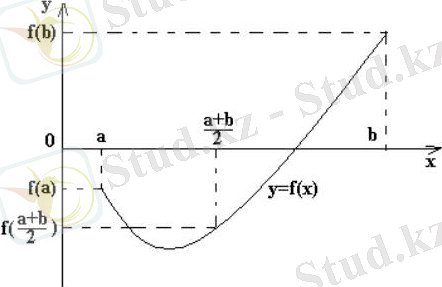
2. 1 сурет - Жартыға бөлу әдісі
Мысал 2. 1 . Жартыға бөлу әдісімен 0, 01 дәлдікке дейін 2 sin ²x+3х 3 -
- 7 = 0теңдеуді шешу.
Шешуі. Қарастырылатын түбірдің оқшаулау интервалы жоғарыда анықталған, бірақ оныy = 2 sin ²x, y = - 3х 3 + 7 = 0функциясының графигін тұрғызып табуға болады. [1, 2] ара қашықтығын жартысынан бөліп, c1= (a + b) /2 = (1 + 2) /2 = 1, 5 аламыз және f(c1) =f(1, 5) = 5, 115 > 0 есептейміз. Демек, белгісіз түбір [1; 1, 5] аралығында жатыр.
c2= (1+1, 5) /2 = 1, 25; f(c2) = f(1, 25) = 0, 661 > 0 деп аламыз. Нәтижесінде
белгісіз түбір [1; 1, 5] аралығында жатады.
Осы үдерісті жалғастыра отырып, алатынымыз:
c3 = 1, 25; f(c3) = f(1, 125) = -1, 1 < 0; ара қашықтық [1, 125; 1, 25] ;
c4 = 1, 187; f(c4) = f(1, 187) = -0, 256 < 0; ара қашықтық [1, 187; 1, 25] ;
c4 = 1, 218; f(c4) = f(1, 218) = 0, 193 > 0; ара қашықтық [1, 187; 1, 218] ;
c5= 1, 202; f(c5) = f(1, 202) =- 0, 0427< 0; ара қашықтық [1, 202; 1, 218] ;
c6= 1, 210; f(c6) = f(1, 210) = 0, 0654> 0; ара қашықтық [1, 202; 1, 210] ;
c7= 1, 206; f(c7) = f(1, 206) = 0, 0075> 0; ара қашықтық
Осылайша, біз [1, 201; 1, 210] ара қашықтығын алдық. Осыдан көрініп
тұрғандай, 0, 01 дәлдікке дейінгі ізделініп отырған түбір x = 1, 206.
2. 2. Кесіндіні қақ бөлу - дихотомия әдісі
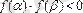 (2)
(2)
(1) теңдеу берілсін.
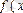 функциясы
функциясы
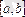 кесіндісінде үзіліссіз болсын және (2) теңсіздік орындалсын.
кесіндісінде үзіліссіз болсын және (2) теңсіздік орындалсын.
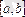 кесіндіде жатқан (1) теңдеудің түбірін табу үшін осы кесіндіні қақ ортасынан бөлеміз.
кесіндіде жатқан (1) теңдеудің түбірін табу үшін осы кесіндіні қақ ортасынан бөлеміз.
Егер
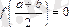 болса, онда
болса, онда
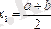 берілген теңдеудің түбірі болып табылады, ал кері жағдайда, егер
берілген теңдеудің түбірі болып табылады, ал кері жағдайда, егер
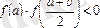 ,
,
онда
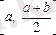 кесіндіні қарастырамыз, әйтпесе
кесіндіні қарастырамыз, әйтпесе
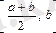 кесіндіні қарастырамыз.
кесіндіні қарастырамыз.
Әрі қарай
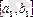 , яғни
, яғни
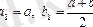 немесе
немесе
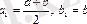 кесіндісін тағы қақ бөлеміз. Нәтижесінде қандай да бір қадамда не (1) теңдеудің дәл түбірін аламыз, не бір бірінің ішінде орналасқан
кесіндісін тағы қақ бөлеміз. Нәтижесінде қандай да бір қадамда не (1) теңдеудің дәл түбірін аламыз, не бір бірінің ішінде орналасқан
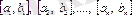 шектеусіз тізбектерді аламыз.
шектеусіз тізбектерді аламыз.
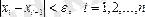 (3)
(3)
жағдайда итерациялық процесті тоқтатамыз. Шешімнің қателік бағасының формуласы
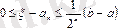
МЫСАЛ 1.
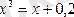
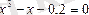 теңдеудің түбірлері жатқан аралықты табу керек.
теңдеудің түбірлері жатқан аралықты табу керек.
Шешуі.
1)
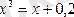 , яғни
, яғни
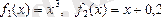 ;
;
2) Осы функциялардың графиктерін саламыз
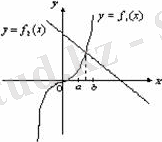
3)
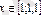 .
.
4)
 ,
,
яғни
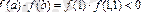 .
.
Жауабы:
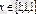 .
.
МЫСАЛ 2.
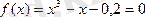 теңдеудің [1; 1, 1] кесіндісінде жататын түбірін жартылай (қақ) бөлу әдісімен дәлдігі e=0, 01 болғанда табу керек.
теңдеудің [1; 1, 1] кесіндісінде жататын түбірін жартылай (қақ) бөлу әдісімен дәлдігі e=0, 01 болғанда табу керек.
Шешуі.
1қадам
.
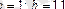 , онда
, онда
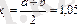
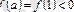 ,
,
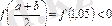 ,
,
яғни (2) теңсіздік орындалмайды, сондықтан келесі кескінін қарастырамыз
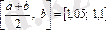 .
.
2 қадам.
 , онда
, онда
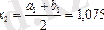 ;
;
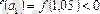 ,
,
 ,
,
яғни (2) теңсіздік орындалмайды. (3) теңсіздікті тексереміз
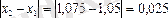 .
.
Сондықтан
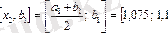 кескінін қарастырамыз.
кескінін қарастырамыз.
3 қадам.
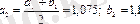 онда
онда
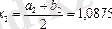 ;
;
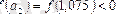 ,
,
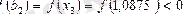
(3) теңсіздікті тексереміз:
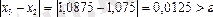 ,
,
сондықтан
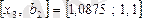 кескінін қарастырамыз.
кескінін қарастырамыз.
4 қ
адам.
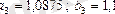 , онда
, онда
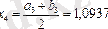 ;
;
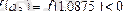 ,
,
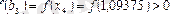 ,
,
яғни (2) теңсіздік орындалады. (3) теңсіздікті тексереміз
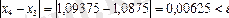 .
.
Жауабы:
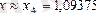 .
.
2. 3 Хордалар әдісі
Әдістің негізіне қарама-қарсы таңбалы екі мәннің сызықтық
интерполяция функциясы жатады. Хордалар әдісі жартыға бөлу әдісіне
қарағанда аз ε мәні үшін аздаған арифметикалық операциялармен есепті
шешуге жағдай жасайды.
[a, b] аралығында f(x) теңдеуінің түбірін табу керек болсын делік. Мұнда
f(x) [a, b] және f(a) f(b) < 0үздіксіз болсын. Бұдан басқа, пусть
f’(x) пен f”(x) [a, b] арасында өз таңбасын сақтайды дейік. f(x) функциясын
[a, b] арасында (a, f (a) ) и (b, f(b) ) нүктелері арқылы өтетін тура теңдеу құра
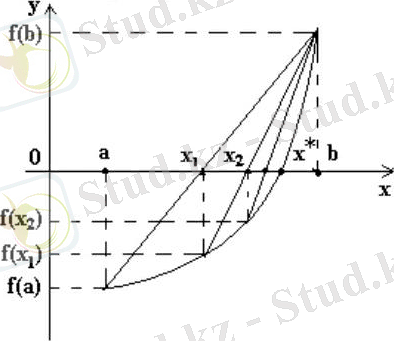
отырып, сызықты функциямен алмастырамыз ( 2. 2-суретін қараңыз) :
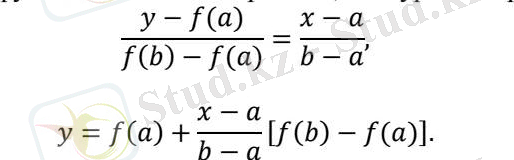
2. 2 сурет - Хордалар әдісі
y = f(x) = 0 екенін ескеріп, x1түбірдің бірінші жуықталған мәнін формула арқылы:
x 1 = a - f(a) ((b - a) /(f(b) - f(a) ) )
Әрі қарай [a, x 1 ], [x 1, b] аралықтарын қарастырамыз және олардың ішінен қайсысының соңында f(x) функциясы қарама-қарсы таңбалы мәндерге ие болады, соны таңдап аламыз. Таңдап алынған аралықта тағы сондай есептеулер жүргізіп, Тапсырылған дәлдікпен (2. 1) теңдеуінен түбір алғанша x 2 түбіріне екінші жуықтауды аламыз.
Егер x*- [a, b] арасындағы оқшауланған f(x) = 0 теңдеуінің нақты түбірі болса, aл ε- түбірдің хордалар әдісімен табылған жуықталған мәні болса, онда бұл жуықталған мәннің қателігі былай бағаланады:
Әдістің алгоритмі былай. Итерациялық үдеріс басталғанға дейін оның көмегімен шешуге ε дәлдігін және түбірі бар [a, b] аралығын береміз Содан кейін:
а) Түбірге жуықтауды есептейміз:
x= a - f(a) ((b - a) /(f(b) - f(a) ) )
б) f(x) <ε теңсіздігінің орындалуын тексереміз, егер бұл теңсіздік орындалатын болса, онда x шешуі деп қарастырамыз, егер орындалмаса, есептеуді жалғастырамыз.
с) f(x) f(a) <0 шартын тексереміз, егер бұл шарт орындалса, x = b деп аламыз, керісінше болған жағдайда x = a және есептеулерді а бөлімінен бастап қайталаймыз.
Мысал 2. 2. 2 sin ²x+3х 3 - 7 = 0 теңдеуін 0, 01 дәлдікпен шығару керек.
Шешуі. Алдыңғы мысалдан көрініп тұрғандай, оң түбір [1; 1. 5] жатыр.
Түбірдің бірінші жуықталған мәнін формула бойынша табамыз:
x 1 = 1 - f(1) ((1, 5 - 1) /(f(1, 5) - f(1) ) ) = 1, 167
f(1, 167) = -0, 5407 <0, болғандықтан [1, 167; 1, 5] аралық бойынша
хордалар әдісін қолданамыз:
x 2 = 1, 167 - f(1, 167) ((1, 5 - 1, 167) /(f(1, 5) - f(1, 167) ) ) = 1, 198 f(1, 198) = -0, 107 <0
Үшінші жуықталған мәнін табамыз:
x 3 = 1, 198 - f(1, 198) ((1, 5 - 1, 198) /(f(1, 5) - f(1, 198) ) ) = 1, 204 f(1, 204) = -0, 021<0
Төртінші жуықталған мәнін табамыз:
x 4 = 1, 204 - f(1, 204) ((1, 5 - 1, 204) /(f(1, 5) - f(1, 204) ) ) = 1, 205 f(1, 205) = -0, 006 <0
Демек, 0, 01-ге дейінгі дәлдікпен ізделініп отырған түбір 1, 205
2. 4 Қию әдісі
Бұл әдіс хордалар әдісімен жүзеге асырылады, тек a мен b ғана түбірден алынады және тіркелмейді. Әдісті геометриялық талдап былай түсіндіреді (2. 3 суретті қараңыз) . Нүктелер арқылы түзу жүргіземіз (қиятындай) ОХ осімен қиылысқанша. x 2 нүктесін аламыз және одан y = f(x) функциясының графигімен қиылысқанша ОХ осіне перпендикуляр түсіреміз. b 2 нүктесін аламыз. a 4 = b 0 мен нүктелері арқылы қима жүргіземіз - x 3 нүктесін аламыз (қиманың ОХ осімен қиылысы) және т. б
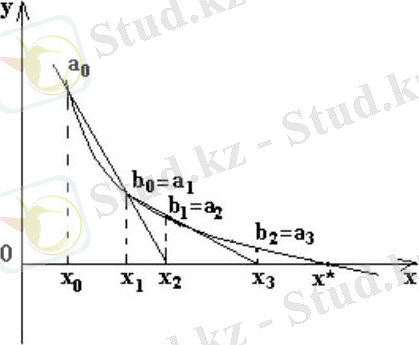
2. 3 сурет - Қию әдісі
Бұл әдіс кесіндіні қаққа бөлу әдісіне қарағанда шешімге тез жинақталады.
Алгоритмі:
- хn, xn+1аралығында f (x) және f (xn+1) функцияларының таңбасы бір біріне қарама-қарсы және түбірі бар болсын.
- Осы екі шеткі нүктеден хорда жүргізіп, хорданың х осімен қиылысқан нүктесін мына формуламен анықтаймыз.
f ( x n+1 ) - f ( x n+1 )
x* = ( x -x n ) + f (x n ) (2. 4)
x n+1 - x n
Егер f(a) >0 шарты орындалса, а нүктесі тұрақты болады да
x * = a- f(a) ((b -a) /( f(b) - f(a) ) )
Егер f(b) >0 шартыорындалса, b
X * = b -f(b) ((a - b) /( f(a) - f(b) ) )
- х*нүктесіндегі функция мәнін F(x*) -ны есептеу. Оның таңбасын екі шеткі нүктедегі функцияның таңбасымен салыстырылады. Егер f (xn) және f(x*) функциясының таңбасы бірдей болса, онда хорданы xn+1және x*нүктесі арқылы жүргізіледі. Оның мәнін (2. 4) формуламен табады. Егер f(xn+1) мен f(x*) функцияның таңбалары бірдей болса, онда хорданы xnжәне x*нүктесі арқылы жүргізіледі.
Шыққан нүктенің мәні (2. 4) формуламен есептелінеді.
- x*нүктедегі мәнін есептеп, мәні нөлге жуық болсаxk+xk- 1<e, онда x*нүктесі (2. 1) теңдеудің түбірі деп аталады. Егер нөлге жуық болмаса, онда процесс жалғасады.
Алдындағы мысал үшін программасы келесідей болады:
2. 5 Ньютон әдісі
Әдіс f(x) ОХ осімен қиылысуы x 1 жуықтауды және т. б. беретін қиманың бастапқы жуықтау нүктесіне алмасуына негізделген. 2. 4-суреттекелтірілген. x* түбіріне бастапқы жуықтауды қандайда бір x 0 алып, x 0 . Оның y = f(x) функциясының графигімен нөл ізделін етін қиылысу нүктесінде қисыққа жанама жүргізеді. ОХ осімен жанаманың қиылысу нүктесі түбірге жаңа x 1 жуықтауды береді. Бұдан кейін үдеріс x 1 нүктесі және т. б. үшін қайталанады.
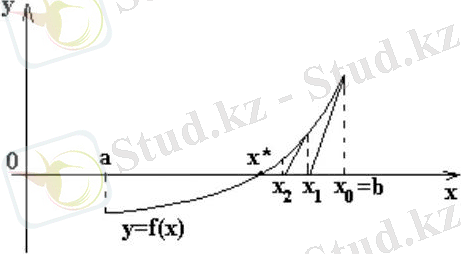
2. 4 сурет - Ньютон
x 0 нүктесіндегі жанама теңдеуі - бұл f’(x 0 ) бұрыштық коэффициенті бар
( x 0 , f(x 0 ) ) берілген нүкте арқылы өтетін түзу теңдеуі:
y - f(x 0 ) = f’(x 0 ) (x - x 0 )
Бұл жанаманың ОХ осімен қиылысу нүктесінде шамасы нөлге тең болады:
-f(x 0 ) = f’(x 0 ) ( x 1 - x 0 ) .
Осыдан x 1 мәнін аламыз:
x 1 = x 0 - (f(x 0 ) /f’(x 0 )
Жалпы жағдайда кезекті жуықтау алдыңғы жуықтау арқылы Ньютон формуласы арқылы жазылады:
x k+1 = x k - (f(x k ) /f’(x k ) (2. 2)
Егер түбірдің бастапқы жуықталған мәні берілген болса, онда (2. 2) формуласы бойынша ізделініп отырған түбірдің кез-келген жуықтауы табылады, демек, x i шексіз сандар қатарын алуға болады, i=1, 2, 3, . . . Егер бұл қатар сай келсе, онда оның шегі ізделініп отырған түбірдің шын мәні болуы керек. Бірақ түбірдің бұл мәніне жету үшін итерацияның шексіз санын орындау керек. Сондықтан осындай есесптеу үдерісін аяқтау үшін теңдеудің берілген дәлдігімен анықталатын шарт болуы керек. Ол мына түрде болады:
x k+1 - x k <ε (2. 3)
Түбірдің бастапқы жуықтауын таңдауда мына ережені ұстану керек: функция таңбасы екінші туындының таңбасымен сәйкес келетін [a, b] кесіндісінің ұшын бастапқы нүкте ретінде таңдау керек. Бірінші жағдайда f(b) f”(x) > 0 және бастапқы нүкте x 0 = b, екінші жағдайда f(a) f”(x) > 0 және бастапқы жуықтауды x 0 = a деп аламыз.
Ньютон әдісімен табылған түбірдің жуықтау мәнінің қателігін бағалау үшін мына теңсіздікті пайдалануға болады
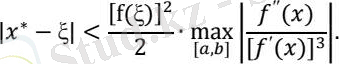
Жанамаларәдісімен (2. 1) :
а) ;
б) мәндерінқабылдайды;
в) (2. 2) ;
г) (2. 3) шартытексеріледі; егеролорындалса, , алегер (2. 3) шартыорындалмаса, .
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz