Фурье интегралдық түрлендірулері

Қазақстан Республикасының Білім және Ғылым министрлігі

Л. Н. Гумилев атындағы Еуразия Ұлттық Университеті

СУЛТАНХОДЖАЕВА МАФТУНА ТОЛКУНБАЕВНА

«Фурье интегралы ұғымын пайдаланып толқындық және жылуөткізгіштік теңдеулеріне қойылатын есептердің шешімін табу».

ДИПЛОМДЫҚ ЖҰМЫС

Мамандық 5B060100 - «Математика»

Нұр-Сұлтан 2019

Қазақстан Республикасы Білім және Ғылым Министрлігі

Л. Н. Гумилев атындағы Еуразия ұлттық университеті

«Қорғауға жіберілді»

Іргелі математика

кафедрасының меңгерушісі

Алдай Мақтагүл

ДИПЛОМДЫҚ ЖҰМЫСЫ

Тақырыбы: «Фурье интегралы ұғымын пайдаланып толқындық және жылуөткізгіштік теңдеулеріне қойылатын есептердің шешімін табу»

5B060100 - «Математика» мамандығы бойынша

Орындаған: Султанходжаева М. Т

Ғылыми жетекшісі

Іргелі математика

кафедра меңгерушісі м. а.,

ф. -м. ғ. к., доцент Алдай Мақтагүл

Нұр-Сұлтан 2019

Л. Н. Гумилев атындағы Еуразия ұлттық университеті

Механика-математика факультеті

5B060100 - «Математика» мамандығы

Іргелі математика кафедрасы

«Бекітемін»

Кафедра меңгерушісі

201 ж. «»

Дипломдық жұмысын орындауға арналған

Т А П С Ы Р М А

Студент Султанходжаева Мафтуна Толкунбаевна

4-курс, М-43 тобы, 5В060100 - «Математика» мамандығы, күндізгі оқу

бөлімі

1. Дипломдық жұмыстың тақырыбы: « Фурье интегралы ұғымын пайдаланып толқындық және жылуөткізгіштік теңдеулеріне қойылатын есептердің шешімін табу » 2019 ж. «21» желтоқсан айында №1587 ректор бұйрықпен бекітілген.

2. Студент аяқталған жұмыстың тапсыру мерзімі «»20ж

3. Жұмыстың бастапқы деректері: Дипломдық жобаның тақырыбына байланысты көптеген әдебиеттерге шолу жасалды.

4. Дипломдық жұмыста қарастырылатын сұрақтардың тізбегі:

Фурье интегралдық түрлендірулері. Фурье интегралы. Фурье интегралдық түрлендіру мүмкіндігін қамтамасыз ететін шарттар. Соңғы шектерде интегралды түрлендіру. Фурье интегралдық түрлендірулерін шектерде қолдану. Шексіз шектері бар интегралды түрлендірулер (жалпы жағдай) . Кейбір жиі қолданылатын түрлендірулер шексіз. Соңғы интегралды түрлендірулерді қолдану мысалдары. Ауыр жіптің тербелістері туралы есеп. Шексіз ішектің тербелістері туралы есеп.

5. Негізгі әдебиеттер тізімі:

- З. Н. Сыздыкова, А. Ибатов Математикалық физика теңдеулері. -А. : Альманах, 2017, -394б.

-Адамар Ж, Задача Коши для линейных уравнений с частным производными гиперболического типа. М. : Наука, 1978

-Н. С. Кошляков, Э. Б. Глинер, М. М. Смирнов Уравнения в частных производных математической физики. М. : Высшая школа, 1970. -712с.

- Лизоркин П. И. Курс дифференциальных и интегральных уравнений. -Москва: Изд. -во «Наука», 1981. - С. 12-56.

6. Жұмыс бойынша берілген кеңестер (тиісті бөлімдері көрсетілген)

7. Дипломдық жұмысты орындау кестесі.

8. Тапсырманың берілген уақыты

Ғылыми жетекшіф. -м. ғ. к. Алдай Мақтагүл

Тапсырманы орындауға алдым Султанходжаева М. Т.

МАЗМҰНЫ

КІРІСПЕ7

1 ФУРЬЕ ИНТЕГРАЛДЫҚ ТҮРЛЕНДІРУЛЕРІ11

1. 1 Фурье интегралы11

1. 2 Фурье түрлендірулері12

1. 3 Фурье интегралдық түрлендіру мүмкіндігін қамтамасыз ететін шарттар13

2 ФУРЬЕ ИНТЕГРАЛДЫҚ ТҮРЛЕНДІРУЛЕРІН ШЕКТЕРДЕ ҚОЛДАНУ20

2. 1 Соңғы шектерде интегралды түрлендіру20

2. 2 Шексіз шектері бар интегралды түрлендірулер (жалпы жағдай) 24

2. 3 Кейбір жиі қолданылатын түрлендірулер шексіз32

2. 4 Фурье интегралдық түрлендіруін қолданып берілген есептің шешімін табу39

3 СОҢҒЫ ИНТЕГРАЛДЫ ТҮРЛЕНДІРУЛЕРДІ ҚОЛДАНУ МЫСАЛДАРЫ47

3. 1 Ауыр жіптің тербелістері47

3. 2 Шексіз ішектің тербелістері туралы есеп50

ҚОРЫТЫНДЫ. 55

ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР58

КІРІСПЕ

Жан Батес Жозеф Фурье - франциялық математик, Париж Ғылым Академиясының мүшесі (1817) . Франциялық ғалым бұл әдісті өзі зерртегені үшін өз есімін береді. Фурьенің алғашқы енбегі алгебра саласына жатады. Бұл еңбегін математик 1796 жылыотырыста баяндады. Баяндамасында алгебралық теңдеуледің нақты түбірлері, шекаралар арасындағы деректер, алгебралық теңдеулердің нақты түбірлері және толық шешімдері туралы баяндады. Фурье бұл баяндаманы 1820 жылы баяндады. 1818 жылы Фурье Ньтонның сандық теңдеулердің шешу әдісінің шарттарынан туындаған сұрақтарды зерттеді.

Фурьенің сандық әдістердің теңдеулерін шешу туралы яғни “Айқындалған теңдеулер нәтижелері” еңбегі қорытынды жұмыстары болып табылады. Бұл жұмыстары 1931 жылы Фурье қайтыс болғаннан кейін басылып шықты.

Фурьенің негізгі саласы математикалық физика болып табылады. 1807 және 1811жылдар да ол Париж Ғылым Академиясында өзінің алғашқы теориясын яғни қатты денелерде жылудың таралуы баяндамасын жариялады. Ал 1822 жылы әйгілі жұмысы яғни “Жылулардың аналитикалық теориясы” еңбегі баспадан шығарылды. Бұл жұмысы кейіннен математика тарихында үлкен рөл атқарды. Бұл еңбегі жылуөткізгіштіктің математикалық теориясы болып табылады. Кейінірек бұл кітап математикалық физиканың барлық заманауи әдістерінің көзі болды. Осы жұмыста Фурье дифференциалдық жылу теңдеуін шығарып, Д. Бернуллидің жалпы құрылымында көрсетілген идеяларды қамтыды. Белгілі бір шекаралас шарттармен жылу теңдеуін шешу үшін айнымалыларды бөлудің әдісін әзірледі (ол Фурье әдісі) . Бұл әдіс негізінен Фурье қатарларының тригонометриялық функцияларымен ұсынылған.

Фурье қатарлары шекаралық есептерді шешудегі ішінара дифференциалдық теңдеулер теориясында жақсы дамыған құрал болды.

Фурье интегралдар теориясы әлі күнге дейін жасалынған. Алайда соңғы шыққан бірнеше маңызды бөлімдері келесілер: Wiener Tauberian теоремалары, мерзімді түрде дерлік қосымшалар функциялары, квази-аналитикалық функциялар және толық функциялар, Фурье-Стильтес интегралдары, жалпы гармоникалық талдау, жалпыланған Bochner интегралдары. Олардың қысқаша сипаттамасы Bochner1 кітабында келтірілген. Фурье қатарының теориясы оқырманға талдауға, оның ішінде элементтерге таныс болуы керек.

Зерттеленген жұмыстармен Фурье әдісін толқындық және жылуөткізгіштік теңдеулеріне қойылатын есептердің шешімін табуда қолданатын боламыз. Ол үшін алдымен теңдеулер туралы түсінік берейік.

Жылуөткізгіштік теңдеуі - бұл белгілі бір кеңістіктегі температура таралуын және уақыттың өзгеруін сипаттайтын екінші ретті жартылай дифференциалдық теңдеу.

Физикадағы толқындық теңдеу - үздіксіз бұқаралық ақпарат құралдарында (акустика, негізінен желілік: газдарда, сұйықтар мен қатты заттарда) және электромагнетизмде (электродинамикада) жұқа мембранадан немесе жолдың шағын көлденең тербелістерін анықтайтын сызықтық гиперболалық жартылай дифференциалдық теңдеу. Ол сондай-ақ теориялық физиканың басқа салаларында қолданылады. Бұл математикалық физикадағы негізгі теңдеулер.

Дипломдық жұмыстың мақсаты Фурье интегралы ұғымын пайдаланып жылуөткізгіштік және толқындық теңдеулерді зерттеу. Сондықтан зерттеу нысаны ретінде Фурье интегралын қолдану болды. Есептің оңай шешілуі үшін барлық жағдай ескерілді. Есептеу тәжірибелерінің нәтижесінде жылуөткізгіштік және толқындық теңдеулерді шешу процестерінің тез орындалуы есепте қателіктің аз болуына мүмкіндіктер береді. Интегралды түрлендірулерді қолданудың ұқсас идеясы және жеке туындысы бар теңдеулер үшін есептерде интегралды түрлендіруді таңдауға ұмтылады: ол дифференциалдық операцияларды айнымалылардың бірі бойынша алгебралық операциялармен алмастыруға мүмкіндік береді. Бұл сәтті болғанда, түрлендірілген тапсырма әдетте бастапқы оңайырақ. Түрлендірілген есептің шешімін тауып, кері түрлендірумен бастапқы шешім де табады. Жеке туындысы бар теңдеулерге интегралдық түрлендірулерді қолданудағы операциялық есептеуден негізгі айырмашылығы интегралдық түрлендірулердің неғұрлым кең жиынтығын пайдалану болып табылады, бұл теңдеулер коэффициенттері айнымалы болған кезде маңызды.

Біз бұл тақырыпты зерттемес бұрын Фурье жайлы барлық анықтамаларды біліп алуымыз керек. Яғни мектеп кезінде және математикалық талдау сабағынан бізге таныс болған Фурье қатарлары туралы білу өте қажет. Айта кететін жәйт, Фурье интегралы тарауында Фурье қатары толық анықтамаға ие екендігіміз айтылады. Сонымен Фурье қатары жайлы айтып өтейік.

Фурье қатары. Фурье қатары математикалық физикада, электротехникада үлкен рөл ойнайды. Олардың жеке жағдайы - тригонометриялық Фурье қатары.

Фурье қатары функционалдық қатарлардың дербес түрі. Функционалдық қатары деп төмендегі теңдеуге айтылады:

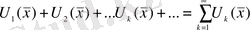
Теңдеудегі 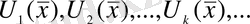, 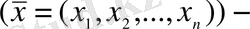тәуелсіз айнымалыларға тәуелді функциялар болады. Функционалдық қатар 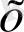тәуелсіз айнымалысының жеке-жеке бекітіп алынған 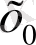мәнінде төмендегі сандық қатарға ауысады.

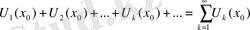
Функционалдық қатардың жинақталу нүктелерінен тұратын құрамды қатардың жинақталу облысы деп атаймыз. Математикалық талдау бабында функционалдық қатардың дербес түрі мынадай:

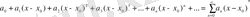
Оның жинақталу облысы бір нүктесінен, немесе центрі 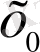нүктесінде орналасқан радиусы 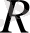- ақырлы санына тең аралықтан, немесе аралығындағы барлық нүктелерден тұрады. Жалпы жағдайда функционалдық қатардың анықталу облысын табу қиын есептердің бірі .

Тригонометриялық қатарлар теориясында ортонормаланған функциялар жүйесін қарайық. 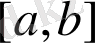сегментінде

(*)

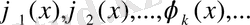функциялар тізбегі берілсін. Егерде әр оң 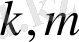үшін 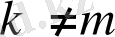болса

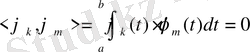
Ал 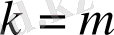болса

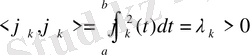
онда (*) тізбегін ортогональды жүйе деп атаймыз.

Егерде (*) тізбегінің әр мүшесінің нормасы бірге тең болса,

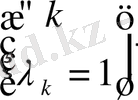
онда (*) теңдігін нормаланған жүйе деп атаймыз.

1 ФУРЬЕ ИНТЕГРАЛДЫҚ ТҮРЛЕНДІРУЛЕРІ Фурье интегралы

Демек біз осы тарауға келгенде Фурье қатары жайлы көп анықтамаға ие болдық. Ендігі мақсат Фурье интегралын зерттеу. Яғни біз Фурье қатарына -периодты интегралданатын функцияларды жіктеуді зерттедік. Онда

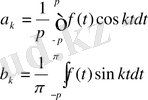
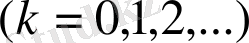(1. 1. 1) -(1. 1. 2)

бұл Фурье коэффициенттері. Солар арқылы

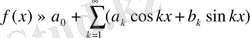
Фурье қатары анықталды.

(1. 1. 1) -(1. 1. 2) анықтамада барлық теріс емес бүтін сандарды бейнелейтін дискретті 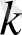индексін барлық теріс емес нақты сандарды бейнелейтін 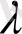үзіліссіз айнымалысына алмастырып,

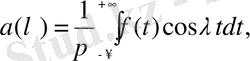
(1. 1. 4) -(1. 1. 5)

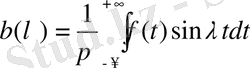
aнықтамаларына, (1. 1. 3) формуласында 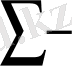таңбасын 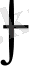таңбасымен 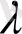интегралдау айнымалысымен ауыстырып,

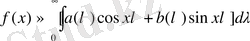
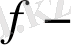функциясының Фурье интегралына келеміз.

(1. 1. 4) -(1. 1. 5) бойынша Фурье интегралы төмендегідей түрленеді.

(1. 1. 6)

Фурье түрлендірулері

нақты мәнді айнымалылары мен 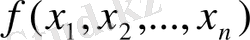функциялары 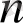нақты айнымалылардың функциясы түрінде салыстырылады,

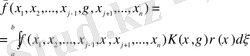(1. 2. 1)

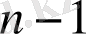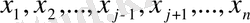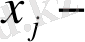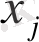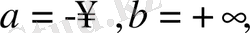
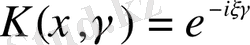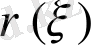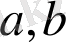
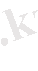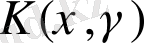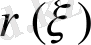нақты айнымалылары, нақты мәнді айнымалысымен гамма өзгерісі, жалпы айтқанда, айнымалы бойынша интегралды түрлендіру деп аталады. Айнымалы - айнымалылар түрлендіруі деп аталады. Интегралды түрлендірулер(1. 2. 1) түрлендіруінің шектерімен, ядросымен және өлшеу функциясымен анықталады. шектері шексіз болуы мүмкін, және функцияларының қасиеттері төменде орнатылады. 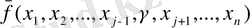функциясын функцияның интералдық түрлендіруі деп аталады, және интералдық трансформациясы немесе 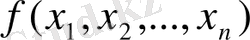функциясының түрі деп ата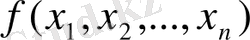лады. жиі түпнұсқа немесе функцияның көрінісі деп аталады. 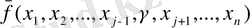функциясы қайта 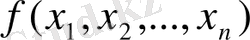функциясына түрлендірілетін түрлендіргіші кері интегралды түрлендіргіші (1. 2. 1) немесе жай кері түрлендіргіші деп аталады. Бұндай жағдайда түрлендіруі (1. 2. 1) тура деп аталады. Фурье интегралдық түрлендіруін қолдану үшін 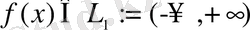болуы жеткілікті. Интегралды түрлендіру (1. 2. 1) оң жағында интеграл болған кезде анықталды. Интегралды түрлендірулерді практикалық қолдану үшін, алайда, кері түрлендірулер де бар болғаны маңызды, олар (1. 2. 1) мен бірге функцияның екі сыныбы арасында өзара бір мәнді сәйкестікті орнатуы мүмкін: 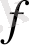функциясының бастапқы класы және 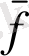функциясының класы, олардың интегралды түрлендірулері болып табылады. Бұл жағдайда екі кластағы функциялар мен бір кластағы функциялар үшін берілген міндеттерді шешу арасындағы сәйкестікті орнатуға болады, басқа кластағы функциялар үшін оңай болатын міндеттерге әкелуі мүмкін. Осы соңғысын шешіп, кері түрлендіру арқылы бастапқы есептің шешімін табады. Интегралды түрлендірулерді қолдану идеясы ұқсас және жеке туындысы бар теңдеулер үшін есептерде: дифференциалды операцияларға мүмкіндік беретін интегралды түрлендіруді таңдауға ұмтылады. Бұл сәтті болғанда, түрлендірілген тапсырма әдетте бастапқы оңайырақ. Жеке туындысы бар теңдеулерге интегралдық түрлендірулерді қолданудағы операциялық есептеуден негізгі айырмашылығы интегралдық түрлендірулердің неғұрлым кең жиынтығын пайдалану болып табылады, бұл теңдеулер коэффициенттері айнымалы болған кезде маңызды.

Сонымен, Фурье интегралдық түрленідіруне ауыстыру формуласы

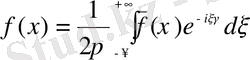
Теңдіктің дұрыстылығының жеткілікті шарты 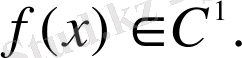Соңғы уақытта Фурье түрлендіруі және ауыстыру формуласын бір біріне симметриялы түрде жазылады, яғни 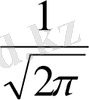интегралдық көбейткішін 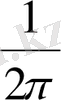орына жазылып жатыр. Бірақ біз, оны жұмысымызда қолданбаймыз. Егер 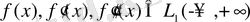онда алдынғы тараулардағы анықтамаларды қолдана отырып мынадай түрде жаза аламыз,

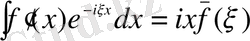
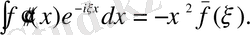
Бұдан шығатын қорытынды, 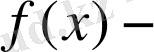функциясының бірінші және екінші туындысы функцияның өзін бейнеленген және осы мағынада Фурье түрлендіру Лаплас түрлендіргішіне ұқсайды. ЖК Фурьеден соңғы айырмашылығы, 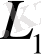тиісті емес функцияларға да қолдануға болатындығы.

1. 3Фурьеинтегралдық түрлендіру мүмкіндігін қамтамасыз ететін шарттар

Екінші ретті дифференциалдық теңдеуін қарастырайық:

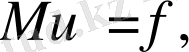(1. 3. 1)

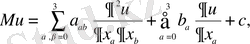(1. 3. 2)

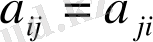- айнымалы коэффициенті екінші ретті дифференциалдық өрнегі,

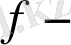берілген функция.

Берілген айнымалылардан біреуін түрлендірулердің айнымалысы ретінде таңдаймыз 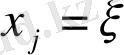, ал қалған айнымалыларды параметр деп қарастырамыз 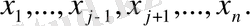Айталық, және 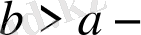өзгеру шегі 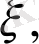және олар шексіз болсын. Жалпы жағдайда, 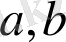шегі 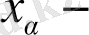параметріне тәуелдіболуыда мүмкін. Бұл интегралды түрлендіруді орындау мүмкіндігін жоққа шығармайды, бірақ түрлендірілген теңдеуді қиындатады, бұл ортақтықтың осы дәрежесіне ұмтылу мағынасы жоқ.

Сондықтан біз төмендегідей қарастырамыз,

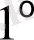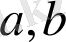. шектері айнымалы түрлендіруді өзгерту 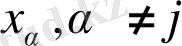параметрлерге байланысты емес. (1. 3. 1) теңдеуді 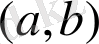интервалында өзгеріске ұшырап, айнымалының өзгеруін (1. 3. 1) түрді интегралды түрлендіруге аламыз :

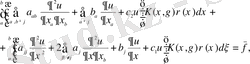(1. 3. 3)

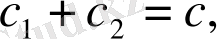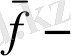ал интегралдық түрлендіру. Біз бұл интегралдық қатынасты интегралдық түрлендіруге қатысты дифференциалдық теңдеуге айналуы мүмкін болған жеткілікті шарттар ды табуға тырысамыз.

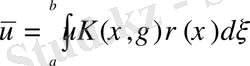
(1. 3. 4)

ізделінді функция. Айнымалы түрлендіру 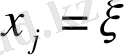бойынша дифференциалды хатты қысқарту үшін келесі есептеулерде штрихпен белгілейтін боламыз.

Айталық,

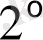. (1. 3. 4) интегралының сол жағы 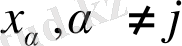параметріне байланыста біркелкі жинақталады, ал интегралдар бұл параметрлердің үздіксіз функциялары болып табылады.

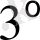. (1. 3. 2) дифференциалдау өрнегі мына түрде болуы мүмкін:

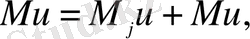(1. 3. 6)

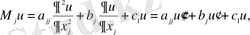(1. 3. 7)

Ал

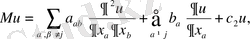
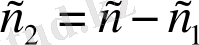дифференциалдық өрнегі, 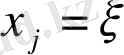айнымалы түрлендіру бойынша туындысы да оған тәуелді коэффициенттер де жоқ.

Бұл мәселеден келесі екі түрлі ой шығады:

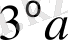. және 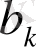коэффициенттері бұл ретте 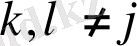болғанда 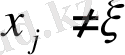ға тәуелді емес.

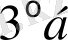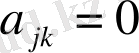. бұл жағдайда .

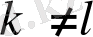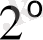қасиетке қарағанда (1. 3. 4) интегралдық түрлендіруінің сол жағын интегралу ретін 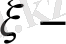бойынша ауыстыруға болады, ал дифференциалау ретін 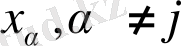бойынша. Онда 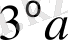бұл қасиет интегралдық түрлендіруді мынадай түрге келтіреді:

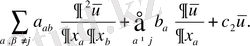
Айта кетейік, бұл түрлендіру (1. 3. 5) формальдыауыстыруына эквивалентті:

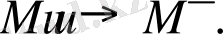
Екінші интегралды (1. 3. 4) сол жақ бөлігін бөліктер бойынша интегралдаймыз.

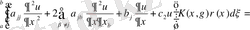
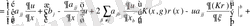
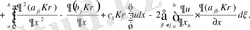(1. 3. 8)

Теңдіктің оң жағы 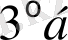қасиетін ескергенде нольге айналады. Түрлендіру теңдеуінде интеграл болмайды,

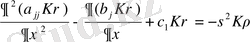(1. 3. 9)

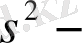арақашықтық 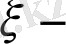ге тәуелсіз. Онда

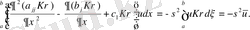
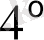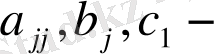. коэффициенттері 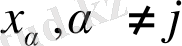ге тәуелсіз.

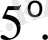
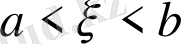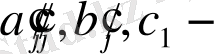
өлшемдері 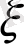бойынша үзіліссіз, ал .

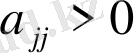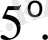шартында (1. 3. 9) теңдігі 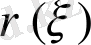- салмақты функциясын таңдағанда өзіндік ұштасқан тірде түрлендіруге болады. Ол үшін теңдеуді мына түрде жазып алайық,

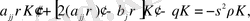(1. 3. 10)

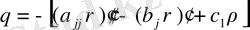(1. 3. 11)

(1. 3. 11) 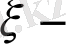түрлендіруі бойынша үзіліссіз функция. Мына шартпен 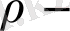функциясын табайық.

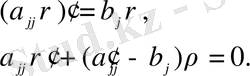(1. 3. 12)

Бұл теңдіктен шығады,

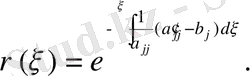
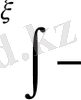интегралының мағынасы: төменгі шегі 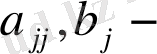коэффициенттерін анықтауды 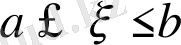интервалының ішіндегі кез-келген нүкте болуы мүмкін. 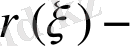салмақты функциясы 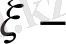дың кез-келген мәнінде 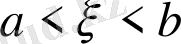интервалында оң мәнді және үзіліссіз екінші ретті туындысы бар. (1. 3. 12) теңдеуі (1. 3. 10) нәтижесінде салмақты функцияны таңдау кезінде көрініс қабылдайды.

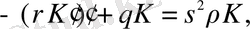(1. 3. 14)

(1. 3. 15)

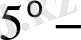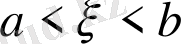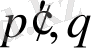қасиетті ескергенде болғанда коэффициент , ал арақашықтық -үзіліссіз.

Айтып өту керек, егер интегралдық түрлендірудің ядросы (1. 3. 9) немесе (1. 3. 14) теңдеуді қанағаттандыра, онда интегралдық түрлендіру қосылғышы 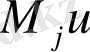(1. 3. 5) теңдеуге формальды түрде эквивалентті болады:

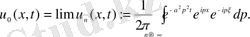
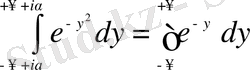
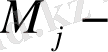дифференциалдық операциясы алгебралық операциясындағы көбейткіш 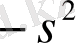қа ауысады.

Оң бөліктен тыс(1. 3. 8) интегралды мүшеге қараймыз. (1. 3. 7) және (1. 3. 12) шарттары бойынша келесі айырмашылыққа тең,

(1. 3. 16)

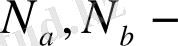өрнектің мәні.

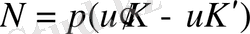(1. 3. 17)

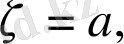
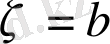болған кезде орынды. 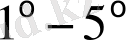қасиеттері бойынша (1. 3. 2) интегралдық түрлендіруі келесідей өзгереді,

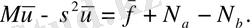
Ядроны дұрыс таңдау кезінде 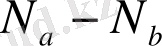айырмасы үшін түрлендіру тек тапсырмада берілген шамалар арқылы ғана көрінуі мүмкін, жеткілікті жорамалдау келесідей.

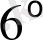. Қосымша берілген есептер екі топқа бөлінеді, олардың біріншісі айнымалы түрлендіру бойынша туындылар және оған тәуелді коэффициенттер жоқ, ал екіншісінде параметрлер мен 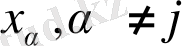бойынша туындылар жоқ және 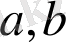шектерде берілген шарттарды білдіреді. Егер бірінші деректер тобында 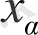бойынша туындылар болса, онда 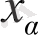бойынша дифференциялау тәртібі және 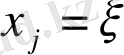бойынша интегралдау өзгеруі мүмкін. Мысалы, шекаралық шарттар

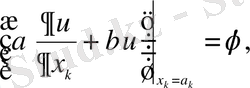
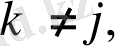
Бірінші топтың түрлендірілген деректері, яғни ауыстыру жүргізілген бірінші топтың деректері

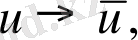
түрлендірілген есептің қосымша деректерінің толық жиынтығын ұсынады. Шын мәнінде, деректердің екінші тобы 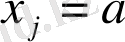және 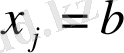шегінде берілген деп болжанады, яғни айнымалы түрлендіру бойынша шарттарды ұсынады. Бірақ айнымалы түрлендіру бойынша деректер түрлендірілген есептің қосымша деректеріне кіре алмайды, өйткені ол шарт бойынша : немесе 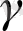бойынша дифференциалды операцияларды қамтымауы тиіс.

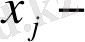ды 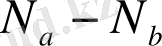ның айырмашылыын есептеуде қолданады. Оны алдағы тарауларда айтамыз. 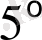-болжам іс жүзінде маңызды жағдайды болдырмайды 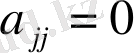, айнымалы уақыт рөлін атқаратын параболалық түрдегі теңдеулерге тән. Бұл жағдайды жеке қарастырайық, сонымен:

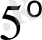. Теңдеу түрі мынадай,

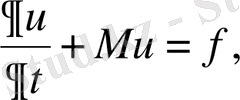(1. 3. 16)

айнымалысы бойынша туындысы жоқ дифференциалдық өрнек.

(1. 3. 16) теңдеуді интегралдық түрлендіру жүргізейік, ядросы 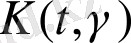шегі 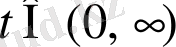болсын. Онда,

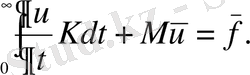(1. 3. 17)

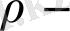өлшемді функциясы бірлікке тең, ал

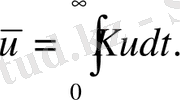
Бөлшектер бойынша интегралдасақ,

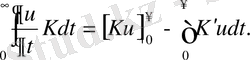
Интегралдық түрлендіруде интеграл белгісі болмайды егерде мынадай алмастыру орындалса,

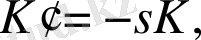(1. 3. 18)

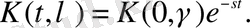(1. 3. 19)

(1. 3. 17) теңдеуді бойынша дифференциалдап келесі теңдікті аламыз,

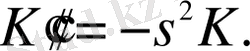(1. 3. 20)

(1. 3. 16) теңдеу (1. 3. 17) теңдеудің шартымен мынандай өзгеріске ұшырайды,

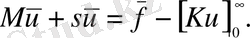(1. 3. 21)

2 ФУРЬЕ ИНТЕГРАЛДЫҚ ТҮРЛЕНДІРУЛЕРІН ШЕКТЕРДЕ ҚОЛДАНУ 2. 1Соңғы шектерде интегралды түрлендіру

Бұл бөлімде интегралдық түрлендіруде 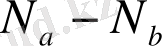айырмашылығын есептеу үшін ядро таңдауды үйренеміз және кері 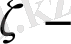айнымалысы бойынша кері интегралдық түрлендіру құрастырамыз.

Айталық, 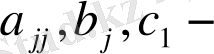коэффициенттері 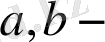нүктелерінде 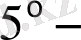қасиеттегі барлық шарттарды қанағаттандырады. Онда 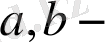нүктесінде шекаралық шарттарда болуы мүмкін,

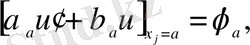(2. 1. 1)

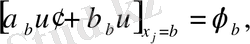
немесе периодтық шарты,

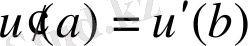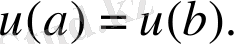; (2. 1. 2)

Штрих белгісі түрлендіруді 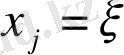айнымалысы бойынша дифференциалдау мағынасын береді.

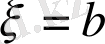болғанда шекаралық шарттарды тексерейік,

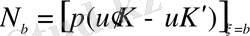(2. 1. 3)

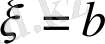жағдайда алдымен 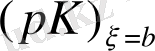үшін (2. 1. 1) теңдеуін шекаралық шарттарға көбейтіп, (2. 1. 3) теңдеуінен 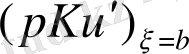алайық. Бұл шыққан теңдеуді 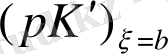көбейтіп, (2. 1. 3) теңдеуінен 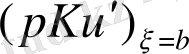алайық. Сонда төмендегідей өрнек аламыз,

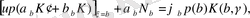
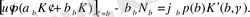
егер 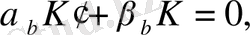онда олар формулалардың бірінің 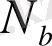мәнін көрсетуге мүмкіндік береді:

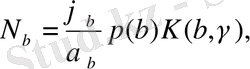
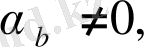(2. 1. 4)

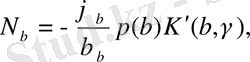
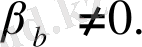(2. 1. 5)

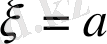төменгі шегі үшін нәтиже ұқсас,

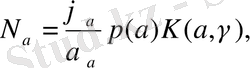
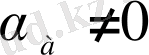(2. 1. 6)

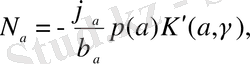
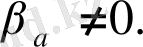(2. 1. 7)

осылайша, алдыңғы параграфтың -шарттары (2. 1. 1) шекаралық шарттары бар есептің интегралдық түрлендірілуі орындалған кезде, егер түрлендіру ядросы (2. 1. 1) сияқты коэффициенттермен біртекті шекаралық жағдайларды қанағаттандырса, онда есептің шығарылуы соңына дейін жеткізілуі мүмкін . (2. 1. 2) шартын ескере отырыптүрленудің ядросы Штурм-Лиувиллдің келесі шекаралық есептерін шешу керек:

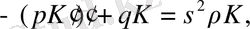(2. 1. 8)

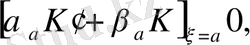
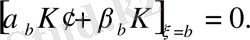(2. 1. 9)

Алдынғы бөлімдерге қарасақ бұл есептің шешуінен шығады,

1. (2. 1. 6) -(2. 1. 9) есеп тек белгілі бір заттай мәндерде ғана бірдей нөлден ерекшеленетін шешімдер барменшікті сандар, олар шексіз өсуші бірізділікті құрайтын, меншікті сандардың спектрі:

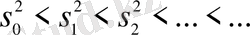(2. 1. 10)

2. Әрбір өз санына бір және бір ғана сызықтық тәуелсіз шешімесептіңсанына тиесілі меншікті функциясы сәйкес келеді. Есептің біртектілігіне байланысты өз функцияларын ерікті түрде нормалауға болады.
3. меншікті функциясыөлшемді функциясымен қос ортогональды, өйткені меншікті функция келесі шарттарды қанағаттандырады,

(2. 1. 11)

4. функциясының интегралы,

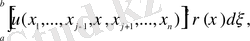(2. 1. 12)

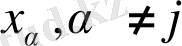параметрлерін қабылдай алатын мәндер жиынтығына қатысты бар және біркелкі шектелген, мүмкін қатар түрінде ұсынылуы мүмкін

(2. 1. 13)

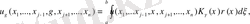(2. 1. 14)

ал теңдік орта есеппен ұқсастық мағынасында түсініледі. (2. 1. 11) және (2. 1. 10) интегралға салынған шарттар, ол үшін алдыңғы тараудың 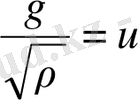, (2. 1. 5) жіктелуінің болу шарттарынан тікелей жүреді.

Егер үшін теңдеу теңдеулердің осындай класына тиесілі болса, онда (2. 1. 11) түрдегі олардың шешімдерінен интеграл жоғарыда тұжырымдалған талаптарды қанағаттандырады, онда (2. 1. 13) формуласы кері түрлендіруді ұсынады. (2. 1. 11) -(2. 1. 13) ыдырау бірлігінен функция мен оның интегралдық түрлендіруі арасындағы өзара мәнді байланыс туындайды . Демек, түрлендірілген тапсырманы шешу арқылы автоматты түрде бастапқы есептің шешімін (2. 1. 11) қатары түрінде аламыз.

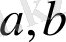шектік нүктелерінде 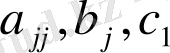коэффициенттерінің ерекшеліктері болуы мүмкін, яғни шексіз алшақтық немесе 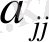коэффициенті нөлге тең. Бұл салдары болуы мүмкін, біріншіден, кері өзгерудің оң бөлігіндегі өрнектің өзгеруі (2. 1. 13) және екіншіден, 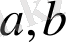шекаралық нүктелерінде шарттардың тұжырымдамасының өзгеруі. Егер 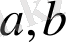нүктелерінде ерекшеліктер әлсіз болса, кері түрлендіру өз көрінісін сақтайды. Нақты тұжырым, бұл әлсіз ерекшеліктер.

Шарттарға қарайық, теңдеудің коэффициенттері ерекшелігі бар 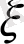шекаралық нүктесінде ядро бағынуға тиіс шарттарға жүгінеміз. Іс жүзінде, әдетте, 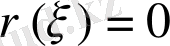іздестірілетін функциясының мәніне және оның туындысына 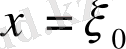кезінде мынадай шарттардың бірі қойылады:

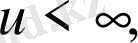(2. 1. 15)

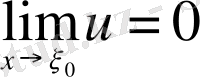немесе 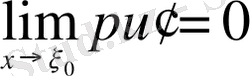(2. 1. 16)

(2. 1. 15) шарты типтік болып табылады, және ол шешімнің біртұтастығын қамтамасыз ету үшін жеткілікті болған жағдайларда, жалпы жағдайда (2. 1. 16) шарттарының біріншісі жалпы жағдайда өте тез, ал екіншісі (2. 1. 15) теңдігінен шығады. (2. 1. 15) -шарт, жалпы айтқанда, ерекшелік жеткіліксіз күшті болған кезде, онда шешімнің біртұтастығын қамтамасыз ету үшін (2. 1. 15) шарттың бірі қажет. Егер ядро іздестірілетін функцияға ұқсас шарттарға бағынса, онда екі жағдайда да,

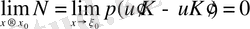(2. 1. 17)

... жалғасы

Функцияны Фурье интегралымен жазып көрсету

Екінші ретті дербес туындылы дифференциалдық теңдеулер

Дербес туындылы дифференциалдық теңдеулер классификациясы

Түрлендірілген Фурье қатарының ең жақсы жуықтауы туралы теорема

Сызықты дифференциалдық теңдеулер

Кездейсоқ кезулердің нақты түрінің математикалық моделі

Математикалық физика теңдеулері

Эллиптикалық тектес теңдеулер

Гиперболалық операторлардың бір класының өз-өзіне түйіндестігін көрсету

Физикадан лекциялар

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс