Макроэкономикалық динамиканың үлгілері

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 20 бет
Таңдаулыға:

Курстық жұмыс

Пәннің аты: Операцияларды зерттеу негіздері

Тақырыбы: Экономикалық динамика және оның үлгiленуi

Мазмұны:

Кіріспе

1. Теориялық бөлім

1.2 Экономикалық динамиканың көрсеткiштерi

1.3 Экономикалық динамиканың теп-теңдiк түсiнiгi. Қарапайым

тепе-теңдiк үлгiсi

1.4 Экономикалық динамика үлгiлерiнiң мысалдары

1.5 Макроэкономикалық динамика үлгiлерi

2 Практикалық бөлім

2.1 Есептің математикалық жолмен шығарылуы жолы

Қорытынды

Пайдаланылған әдебиеттер

Кіріспе

Экономикалық ғылым және тәжiрибемен шешiлетiн мәселелер уақыт факторының
тiркеуiне тәуелдiлiкте статикалық және динамикалық болып бөлiнедi.Статика
нақты мезгiл немесе уақыт аралығына қатысты экономикалық объектiлердiң
қалпын,уақыт мезетiндегi олардың параметрлерiнiң өзгерiсiнiң тiркеуiнсiз
зерттейдi.Динамикалық мәселелерде тек айнымалылардың уақытқа тәуелдiлiгi
ғана емес,сонымен бiрге олардың уақыт мезетiндегi өзара байланысы
бейнеленедi.Мысалы,инвестиция динамикасы негiзгi капитал мөлшерiнiң
динамикасын анықтайды,бұл өз кезегiнде шығарылым көлемiн өзгертудiң маңызды
факторы болып табылады.
Экономикалық динамикада уақыт үзiлiссiз немесе дискреттi түрде
қарастырылуы мүмкiн.Үiлiссiз уақыт үлгiлеу үшiн өте қолайлы,өйткенi ол
дифференциалдық теңсiздiк және дифференциалдық есептеудiң құрылғысын
қолдануға мүмкiндiк бередi.Дискреттi уақыт қосымша үшiн өте қолайлы,өйткенi
статикалық мәлiметтер үшiн дискреттi және нақты уақыт бiрлiгiне
жатады.Дискреттi уақыт үшiн таратылынатын теңсiздiк құрылғысы қолданылуы
мүмкiн.Байқайтынымыз, экономикалық динамиканың көпшiлiк танымал үлгiлерi
үзiлiссiз және дискреттi нұсқаларда болады.Екi нұсқада да олар үшiн
аналогты нәтиже алынуы мүмкiн және үлгiлердiң өздерiнiң қиындық деңгейi
шамамен бiрдей.
Бұл курстық жобада экономикалық динамика көрсеткіштері, экономикадағы
динамикалық тепе-теңдік түсінігі (қарапайым тепе-теңдік үлгісі),
экономикалық динамика үлгілерінің мысалдары, макроэкономикалық динамика
үлгілері тақырыптары қарастырылады.
Жеке тоқталсақ, экономикалық объектінің динамикасын сипаттайтын
көрсеткіштер- бұл абсолютті өсімдер, деңгейлер және өсiмдер қарқыны.Міне,
осы көрсеткіштер туралы қарастырылады.
Экономикалық теорияда тепе-теңдік теориясымаңызды болып табылады,яғни
ішкі әсер жоқ кезде ол сақтайтын объектінің жағдайы. Сондықтан, бұл
тақырыпта тепе-теңдік жағдайындағы қарапайым экономикалық жүйені
қарастырамыз.
Экономикалық динамика үлгілері тақырыбында өрмек тәріздес үлгіні
талдаймыз.
Ал, макроэкономиаклық динамиканың үлгілері ретінде Харрод- Домар және Солоу
үлгілерін қарастырылады.

1.1 Экономикалық динамиканың көрсеткiштерi

Экономикалық объектiнiң динамикасын сипаттайтын көрсеткiштер-бұл
абсолюттi өсiмдер,деңгейлер және өсiмдер қарқыны.Егерде уақытта тәуелдi
А(t) мөлшерi қарастырылса,онда абсолюттi өсiм 0 жағдайынан 1 жағдайға дейiн
мынаған тең: 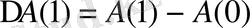, деңгейдің дискреттi қарқыны 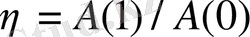,өсiмнiң
дискреттi қарқыны

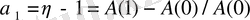
Ағылшын тiлiндегi әдебиеттерде “growth rate” (“деңгей қарқыны”)
терминiн көбiнесе 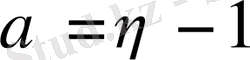көрсеткiшi деп атайды,яғни бiздiң
терминологиямыздағы өсiм қарқыны.
Егер l өсiм қарқыны уақыт мезетiнде өзгертiлмесе,онда
көрсеткiш динамикасы А(t) мына түрде бейнеленуi мүмкiн: ’.
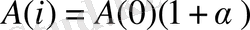Егер А(t) мөлшерi уақыттың үзiлiссiз функциясы болса,онда деңгей
тұрақты қарқынмен мына түрде жазылады: 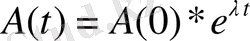, мұндағы e=2,72-ондық
логарифмнiң негiзi, -өсiмнiң үзiлiссiз қарқыны.Ол жалпы жағдайда мына
түрде есептеледi:
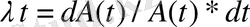немесе

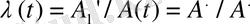
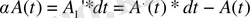дифференциалы, мұндағы 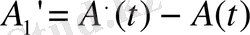функциясының уақыт бойынша туындысы.A(t)
мөлшерінің бойында өсімінің үзіліссіз қарқынымен 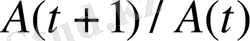деңгейдің
дискретті қарқыны 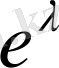- ге
тең,кіші 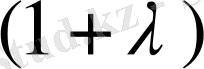-ге жақын яғни, өсімінің дискретті қарқынында
деңгей қарқынына.
Көрсеткіштердің туындысы мен қосындысы үшін өсім қарқынының мөлшерін
қарастырайық.
S(t) көрсеткіші сәйкес және 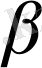тұрақты үзіліссіз қарқынмен
өсетін, 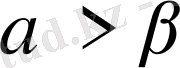A(t) және B(t) қосындысы болсын.Онда

(1)

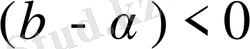болғандықтан, тік жақшадағы мөлшер 1-ге ұмтылады және қосынды
өсімнің қарқыны тез өсетін құраушы қарқынына ұмтылады, яғни -ға. P(t)
мөлшері және 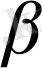өсімінің үзіліссіз қарқынымен бірге A(t) және
B(t) туындысы болсын. Бұл жағдайда

(2)

яғни өсім қарқыны,туындысы көбейткіштер өсімінің қарқындар
қосындысына тең. Егер және 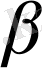- A(t) және B(t) өсімдерінің
дискретті қарқыны болса, онда

(3)

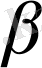Кіші және - да 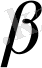мөлшері аз және туынды
өсімінің қарқыны шамамен көбейткіштер өсімінің қарқынының қосындысына тең.
Егер 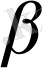туындысы маңызды болса, онда туынды өсімінің қарқыны
шамамен көрсеткіштер өсімі қарқынының қосындысына тең деп
есептелмейді,өйткені оны өсіреді.
Көлемді және қарқынды мөлшердің байланысын туынды функциясының мысалында
оңай көрсетуге болады.
Y(t),K(t),L(t) - өнімінің , капитал және еңбектің көлемді көрсеткіштері
болсын, ал y(t), k(t), l(t) - олардың өсімдерінің үзіліссіз қарқыны болсын.
Көлемді техникалық орташа прогресспен мына түрде болады:

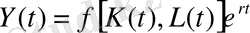(4)
Бұл тәуелділікті логарифмдей отырып,мынаны аламыз:

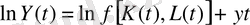(5)

Әрі қарай уақыт бойынша дифференциалдаймыз:

яғни, 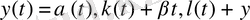(6)

мұндағы 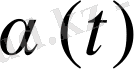және 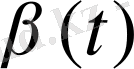- капитал және еңбек бойыншаөнім
созылғыштығы сәйкес.Бұл сызықтық формула өндіріс факторы өсімі қарқынының
кіріс өсімінің ортақ қарқынына үлесін сипаттайды.

1.2 Экономикадағы динамикалық тепе-теңдік түсінігі. Қарапайым тепе-теңдік
үлгісі

Экономикалық теорияда тепе-теңдік теориясымаңызды болып табылады,яғни
ішкі әсер жоқ кезде ол сақтайтын объектінің жағдайы. Экономикалық
динамикалың
мәселесі тепе-теңдік жағдайына шығу процесінің бейнесі ретінде, сондай-ақ
ішкі күштің әсеріндегі осы жағдайлардың өзінің трансформация процесін
қосады. Тепе-теңдік жағдайындағы қарапайым экономикалық жүйені
қарастырайық және үзіліссіз дискретті жағдайлардағы осындай жүйенің
қозғалысын бейнелейік. Бірінші жағдайда жүйе динамикасы дифференциалдық
теңдіктің көмегімен бейнеленеді, ал екінші жағдайда - әртекті теңдік
түрінде.
Дифференциалдық теңдік көрсеткіштер өзгерісін (біздің жүйеміз x(t)
немесе x көрсеткіштерімен бейнеленсін ) 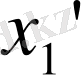немесе x оның қозғалысының
жылдамдығымен байланыстырады.x көрсеткіші өзгерісінің жылдамдығы xe тепе-
теңдік мағынасынан оның ауытқу мөлшеріне пропорционал болсын дейік.
Басқаша сөзбен, егер неғұрлым көрсеткіш тепе-теңдік мағынасынан
ауытқыса, соғұрлым оған оралуға ұмтылады. Егер теңдікте уақыт бойынша тек
бірінші х айнымалысы қатысса, ал байланыс сызықтық болса, онда бұл сызықтық
дифференциалдық теңдік. Ол келесі түрде болсын, мысалы, x=k(x-xe), мұнда k-
коэффициент. Бұл теңдікте kxe- бос мүше,олсыз x=kx теңдігі біртекті деп
аталады және оның ортақ шешімі x=c*ekt. Бастапқы біртексіз теңдеудің x=xe
жеке шешімі бар(егер х мөлшері тепе-теңдік жағдайында
болса), ал оның жалпы шешімі біртексіз теңдеудің жеке және жалпы шешімінің
қосындысы, яғни (сөндіру кезінде) x=xe+c*ekt. t=0 болғанда х мөлшері х(0)
тең екендігін ескерсек,
c=x(0) - xe және x(t)=xe + (x(0)-xe)ekt аламыз.Егер k0, онда
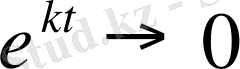және тепе-теңдік тиянақты, яғни x(t) мөлшерінің xe мағынасынан ауытқуы
кезінде, ол тағы осы мағынаны қабылдауға ұмтылады.k0 мөлшер және
сәйкес
x(t) шексіздікке ұмтылады(егер бастапқы жағдай тепе-теңдік қалпымен сәйкес
келмесе).
Жүйе xe қалпына ауысады (1а сур.). Оның k0 жүріс-тұрысын 1б
суретінен көруге болады. Динамикалық жүйенің жүріс-тұрысын мысалы, график
түрінде де бейнелеуге болады(1в - 1г сур.). Дискретті уақыттағы жүріс х
мөлшерін көршілес уақыт моментіне яғни, x1 және xt-1 байланыстыратын
таратылынатын теңдеудің көмегімен бейнеленуі мүмкін.
Мысалы, дискретті жағдайда шешімі
x1=xe+(x(0)-xe)(1+k)t болатын x1=xt-1+k(xt-1-xe) тартылынатын
теңдеу қолданылуы мүмкін.
Бұл шешім xt=(1+k)xt-1 біртекті теңдеу үшін
x1=c(1+k)t-жалпы шешімінің қосындысы түрінде және бастапқы
таратылынатын теңдеу үшін xt=x(0) жеке шешімі түрінде t=0 болғанда xt=x(0)-
ді ескере отырып, табылуы мүмкін.
k0 болғанда xe-ден ауытқу жағдайында жүйе xe бағытында қозғалады, k0
одан әрі қарай қозғалады.-2k0 тепе-теңдік тұрақты және k0 және k-2
тұрақсыз. k-1 х көрсеткіші әрбір уақытта xe тепе-теңдік мағынасына
“секіреді”. k-1 xe-ге жақындау үшін тіптен алыс.

x’(0) x

x1(0) x

xe
xe

x2(0)

x2(0) t
t

1б сур. 1a сур.

x x

xe xe

t
t

1в сур.
1г сур.

1.3 Экономикадағы динамика үлгілерінің мысалдары

Макроэкономикалық динамиканың дискретті және үзіліссіз әдістемені
жүзеге асыратын үлгілердің екі түрін қарастырамыз.Екі жағдайда да үлгілер
ортақ абстракты сипат алады. Сонымен бірге олардың шешімі айқын түрде
табылуы мүмкін және де одан олардың параметрлерінің өзара байланысының
әртүрлі жеке жағдайы үшін маңызды ерекшеліктері шығады. Бұл үлгілерде
дискретті және үзіліссіз динамикалық үлгілеудің қарапайым құрылғысын
көрсетуге, макроэкономикалық динамиканың мәселелері және маңызды
категорияларын суреттеуге қолайлы.

Өрмек тәріздес үлгі
Бұл үлгі нарықтағы уақыт бойынша барлық кешігу кезінде (лаг) сұраныс
пен ұсынстың дәстүрлі қисғымен бейнеленетін тауардың көлемі мен бағасының
тұрақтылығын зерттеуге мүмкіндік береді(2 сур.).
Өндіруші (мысалы тұқым фермасы) қазіргі уақыттағы тауар ұсынысын
алдыңғы уақытта қойылған яғни,Qs(t)=St(Pt-1) бағаның негізінде анықтасын.
Осылайша, ұсыныс функциясына бір уақыт бірлігі ұзақтылығымен уақытша лаг
сыналанып кіреді.
Шындығында да, өнімнің көлемі жөніндегі шешім қазіргі бағаның
тіркеуімен қабылданады, бірақ өндірістік циклдың белгілі- бір ұзақтылығымен
бар және осы шешімге сәйкес ұсыныс нарықтығы берілген цикл аяқталғаннан
кейін пайда болады.

P

S

D

Q

2 сур.

Ұсыныс қисығы тауарға сұрыныс көлемінің қазіргі уақыттағы тауар
бағасына тәуелділігін сипаттайды, яғни Qd (t)=Dt(Pt).
Осылай, баға динамикасын теңдеу жүйесі арқылы бейнелеуге болады:

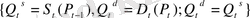
немесе бір теңдеумен Dt(Pt) = St(Pt-1) (7)
Бұл теңдеуден қазіргі ағымдағы уақыт моментіндегі Р бағасының
мағынасын алдыңғы уақыт моментіндегі белгілі Pt-1 мағынасы бойынша табуға
болады.Шешім сызбасы өте қарапайым:

(мұндағы D-1- сұраныстың керісінше функциясы). Жеке жағдай ретінде ұсыныс
пен сұраныс функциясы сызықтық болатын өрмектәріздес үлгіні қарстырайық:
S(p)=A+Bpt-1; D(p)=C-EPt; S(p)=D(p) (8)
Мұнда ұсыныс функциясы өспелі болғандықтан E0; CA0 яғни, D(0)C(0)0
(0-дік бағада сұраныс ұсынысты арттырады деп есептейік).Мұндай жүйенің
динамикасын бейнелейтін теңдеу мына түрде болады:

D(pt) = S(pt-1) немесе C-Ept= A+Bpt-1

Алдымен,р* шамалас бағасын және Q* шамалас өнім көлемін табамыз:

Q*= C-Ep*= A+Bp* , осыдан p*=C-AB+E және Q*
=BC+AEB+E

P P

S S

D
D

Q Q

3а сур.
3б сур.

P

S

D

Q

3в сур.

Әрі қарай өндірістің көлемі мен бағасының жүріс-тұрысын зерттеу
қажет,егер бастапқы нүкте тепе-теңдікпен сәйкес келмесе. Басында бұл
есепті “өрмек” тәріздес суретті ала отырып, графикалық түрде шешуге
болады. Тепе-теңдік нүктесімен сәйкес келмейтін тауардың бастапқы кейбір
көлемі мен бағасын бере
отырып, нүктені көлденең және тік сызықтар арқылы қосып, жүйелі түрде
енгіземіз. Графикалық анализден келесі нәтижелерді алуға болады(3а сур.).
Егер ұсыныс қисығы сұраныс қисығына қарағанда қатты еңкейсе, онда мұндай
нарықтағы тепе-теңдік тұрақты болады(3б сур.). Ақырында, ұсыныс пен сұраныс
қисықтарының тең еңкеюінен нарықта үнемі тұрақты амплитудамен ауытқу (3в
сур.) сыналады. Енді үлгінің формальды анализіне көшеміз. pt-1 арқылы pt-
ны суреттеп, келесі рекурентті қатынасты аламыз: Pt=C-AE=BE . Бұл
қатынасты қадаммен қолдана отырып, мынаны табамыз:

Pt=C-AE-BE*p0 ; P2 =C-AE-BE*(C-AE-BE)*p0 немесе жалпы
түрде:

(9)

Жақша ішіндегі мағына геометриялық прогрессияның қосындысы:
Sn=a1*(1+g+g2+...+gn-1)=a1*1-gn1-g
Егер 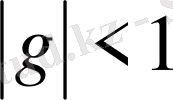, онда lim Sn=a11-g

Өрмектәріздес үлгі үшін g=-BE , a1=C-AE. Бұдан t уақытының
өнім моментіне Pt бағасы үшін мағынаны аламыз:

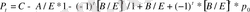(10)

BE1 және Pt=C-AB+E=p* екені анық, яғни ұсыныс қисығының
сұраныс қисығына қарағанда қатты еңкейгенде, тепе-теңдік тұрақты. Егер
BE1, яғни сұраныс қисығы қатты еңкейсе, онда 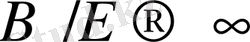және тепе-теңдік
тұрақсыз.
ВЕ=1 яғни, B=E, Pt мағынасы тепе-теңдік мағынасының айналасында
кезектеседі.
Сонымен, жүйенің тұрақтылығы үшін анықталатын момент уақытша
иемденген сол функцияның бағасының өзгерісіне әлсіз, жазушы реакция болып
табылады(мұнда ұсыныс функциясы).
Шындығында да BE1 шексіз өспелі тербеліс болмайды, өйткені тепе-
теңдіктен үлкен ауытқу кезінде сызықтық жақындау мүмкін емес тербелістер
қондырылады, бірақ (соңғы амплитудамен) өндірістің құлдырауы мен өрлеуінің
экономикалық циклының бейнесі болып табылатын соңғы амплитудамен
қондырылады.

1.4 Макроэкономикалық динамиканың үлгілері

Харрод-Домар үлгісі

Үздіксіз уақыт үлгісінің мысалы ретінде
макроэкономикалық Үлгі тұтыну қосындысы мен инвестиция ретінде
қарастырлатын кіріс динамикасын суреттейді. Экономика жабық
деп есептелінеді, сондықтан таза экспорт нөлге тең , ал
үлгідегі мемлекеттік шығындар бөлінбейді. Өсім
үлгісіне негізгі сілтеме - инвестиция мен кіріс өсімі
жылдамдығының арасындағы өзара байланыс формуласы . Кіріс
өсімі жылдамдығы нвестиицияларға пропорционалды деп
жорамалдануда:

I(t)=B*dYdt мұнда B-кіріс өсімнің капиталды сиымдылығы
немесе өсім капитал сиымдылығының коэффициенті (осыған
сәйкес , оған кері 1B мөлшері өсім капитал серпілісі деп
аталады). Осылайша үлгіге келесі сілтемелер қосылады :
• инвестиициялық лаг нөлге тең ; инвестиициялар мезетте
капитал
өсіміне көшеді. Бұл ∆K(t)=I(t) білдіреді , мұнда ∆K(t)-
уақыттағы капитал өсімінің үздіксіз қызметі ;
• капиталдың шығуы жоқ;
• үлгідегі өндірістік қызмет бір сызықта, бұл кіріс өсімнің
капитал өсімінен туындайды ;
d Y ( t ) = 1 B * d ( K ( t )
) d t.
Сызықтық өндірістік қызмет Y(t)=a*L(t)+d*K(t)+C, мұнда
b=1B, бұл қасиетке , егер a = 0, немесе L(t)=Const
болған жағдайда
ие болады. Осылайша келесі сілтеме мынадай болып
келеді .
• уақыттағы еңбек шығыны үнемі , болмаса шығарылым еңбек
шығынына байланысты болмайды, өйткені еңбек жетіспеуші
ресурс болып табылады;
• үлгі техникалық процессті есепке алмайды .
Көрсетілген сілтемелер әрине нақты макроэкономикалық
үрдіс динамикасы суреттеуін қатаңдатады, осы үлгіні қолдануды
қиындатады, мысалы, жиынтық шығарылым немесе кіріс мөлшерін
болжау немесе тікелей есебі үшін . Алайда осы үлгі бұл
үшінде арнамаған, сондай-ақ оның қарапайымдылығы ленвестиция
динамикасы мен шығарылым өсімінің өзара байланысын терең
зертеуге, жасалған сілтемелер кезінде қарастырылатын шөлшемдер
траекториясының дәл формулаларын ашуға мүмкіндік
береді .
Инвестиция көрсеткіші уақытындағы өзара байланыстырушы
тәуелділік , онымен анықталатын негізгі капиталдық көлемі мен
шығарылым деңгейі, макроэкономикалық динамиканың барлық
үлгілерінде базалық болып табылады. Бұдан басқа, бұл үлгілерде
шығарылым ( кіріс ) құрылымының құрылу қағидаларын анықтау , оны
құрастырушылар арасында бөлу қажет,

бастысы - тұтыну мен жинақтау арасында . Бұл қағидалар
оптимизацияланған бағытқа (негізінде бұл белгілі бір түрдегі
тұтынудың жиынтық мөлшерінің максимизациясы), тең салмақты және
өзге де бағыттарға негізделуі мүмкін. Қарастырылатын үлгіде
тұтыну көлемінің динамикасы C(t) экзогенді түрде жорамалданады.
Бұл көрсеткіш уақытта тұрақты болып табылады , берілген тұрақты
жылдамдықпен өсіп немесе қандай да бір өзге динамикаға
ие болуды есептейді (бірінші екі жағдайда үлгі шешімін
жеңіл алуды есептейді).
Егер C ( t ) = 0 деп есептеск , ұлгінің қарапайым нұсқасы
шығады. Бұл жағдай тәжірибелік көзқарас бойынша тіпті шынайы
болмайды , алайда мұнда барлық ресурстар инвестийияға бағыталады ,
осының нәтижесінде өсімнің жылдамдық мүмкіндігінің барынша
техникалылығы анықталуы мүмкін . Бұл жағдайда бізге мынау
шығады:
Y ( t )= C ( t ) + I ( t ) = 0 + B * dY ( t ) d Y ( t )
(11)
Бұл – сызықтың бір текті дифференциялық теңдік , оның
шешімі
Y ( t )= Y ( 0 )* e (1B)t түріне ие (бұл дифференциялаумен
тексеруге жеңіл) . Мұндағы өсімнің үздіксіз жылдамдығы
1B- ге тең . Бұл өсімнің барынша мүмкін техналогиялық
жылдамдығы .
Енді C(t)=C уақыт бойынша тұрақты болсын. Біртексіз
сызықтық дифференциялық Y(t)=BY(t)+C теңдігін аламыз. Оның
жеке шешімі Y(t)=C болып табылады, және оны Y(t)=A*e(1B)t
біртекті теңдіктің жалпы шешімімен қоса , оның t=0 қойып,
A=Y(0)-C=I(0) және Y(t)=(Y(0)-C)*e(1B)t +C ие боламыз. Кіріс
өсімінің үздіксіз жылдамдығы y(t)=Y(t)Y(t), бұл шешімде
y(t)=1B*[1-CY(t)] –тең. Ол уақыттың бастапқы кезенде 1B*[1-
C(0)Y(0)] құрап ( t=0 болған жағдайда ) ,өсе отырып 1B –ге
t→∞ болған жағдайда ұмтылады (бұл түсінікті де, өйткені
керіс өседі , ал тұтынудың тұрақты көлемі оның ең аз
үлесін құрайды) . Жақшадағы a(t)=[1-CY(t)] көлемі t
уақыты кезіндегі жинақтау нормасы , өсімді 1B капитал
серпілісі көрсеткішіне секілді пропорционалды болып келеді .
Сонымен , өзге теңдіктер кезінде жинақтау нормасының
өсімі кіріс өсімі жылдамдығын пропорционалды түрде көбейтеді.
Сондай-ақ бұл

ағымдағы тұтыну деңгейін төмендетеді , өсім жылдамдығы мен
ағымдағы әл-ахуал деңгейін арттыруда бәсекелестік мақсаттарды
келісу мәселесін шешу үшін , ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.