Координаталар өсімшелері

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 11 бет
Таңдаулыға:

Қазақстан Республикасының білім және ғылым министрлігі
Еуразия ұлттық университеті

ПРАКТИКАЛЫҚ ЖҰМЫС

Тақырыбы: Теодолиттік түсіріс.

Орындаған: Ескермесова Л.

ИЖжЖ-13 тобы

Тексерген: Мусайф Г. М.

Нұр-Сұлтан 2020
Мазмұны
І. Теодолиттік түсіріс ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..3

ІІ. Жұмыстың барысы ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ...3

2.1 Тұйық теодолиттік жүрісті есептеу барысы ... ... ... ... ... ... ... . ... ... ... .3-6

2.1.1 Тұйық жүріс ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... .7

2.2 Ашық теодолиттік жүрісті есептеу барысы ... ... ... ... ... ... ... . ... ... ... ... 8

2.2.1 Ашық жүріс ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... 9

2.3 Координаталар өсімдерін есептеу ... ... ... ... ... ... ... ... ... ... ... ... ... 10-12

3.1 Теодолиттік түсірістің планы ... ... ... ... ... ... ... .. ... ... ... ... ... ... ...13-14

ІІІ. Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..15

Теодолиттік түсіріс.
Теодолиттік түсіріс деп теодолит аспабымен орындалатын горизонталь немесе контурлық түсірісті айтады. Теодолитпен горизонталь және көлбеу бұрыштар өлшенеді. Ұзындықтар ленталармен және қашықтық өлшеуіштермен өлшенеді. Осы жұмыстарда бұрыш өлшеуіш аспабы ретінде теодолит қолданылады, ал ара қашықтықты өлшеу үшін ленталар (рулеткалар) және оптикалық қашықтық өлшеуіштер пайдаланылады. Теодолиттік түсіріс геологиялық барлауда, тау кен ісінде, ауыл шаруашылығында, құрылыста т.с.с. пайдаланылатын мәліметтерді алу үшін жүргізіледі. Теодолиттiк жүрiстер тұйықталған, тұйықталмаған және бiр жағы байланыстырылған болуы мүмкін. Тұйықталған теодолиттік жүрiс, әдетте, геодезиялық негiздеудiң пунктiне байланысқан тұйық көпбұрыш түрiнде болады. Тұйықталмаған жүрiстер басы мен аяғында геодезиялық негiздеудiң координаталары белгiлi пункттерiне тiрелуi тиic.

Практикалық жұмыс.

Берілгені: Бастапқы және соңғы дирекциондық бұрыштар, тұйықталмаған теодолиттік жүрістің төбелерін есептеу үшін бастапқы және соңғы координаталар. Теодолиттік жүрісте барлық жақтарының ұзындықтары өлшеніп, жүріс бойынша әрбір нүкте басының оң горизонталь бұрышы өлшенген.
Жұмыстың мақсаты: Бастапқы пункт координатасы және дирекциондық бұрышты өлшеуді үйрену. Координаталық торды квадрат түрінде жақтарын 10см - ден,1:2 000 масштабта сызып, қажетті квадрат санын тұйықталған теодолит жүрісі координаталарының мәнін білу. Тедолиттік жүрісті оның координаталары бойынша тұрғызып, есептелген координаталарды планға түсіру. Теодолиттік жүрістің планын 1: 2 000 масштабта ситуациясымен планға түсіру.
Жұмыстың орындалу реті:
Бұрыштың қиыспаушылығы анықталады. Өлшенген бұрыштардың практикалық қосындысы мен теориялық қосындысының айырмашылығын бұрыштық қиыспаушылық деп атайды.

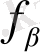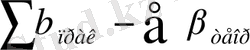= (4)

мұндағы 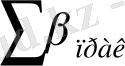- жүріс бойынша өлшенген жазық бұрыштардың қосындысы;
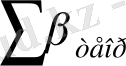- тұйықталмаған жүрістің бұрыштарының теориялық қосындысы;

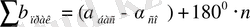(5)

мұндағы n - бұрыштар саны.
Шекті қиыспаушылықты анықтау:
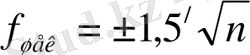(6)
Егер 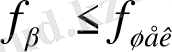болса, онда қиыспаушылық барлық өлшенген бұрыштарға кері таңбамен бөліп таратылып жазылады. Түзетілген бұрыштар ведомостің 3-графасына жазылады.
Теодолиттің жүрістің қабырғаларының дирекциондық бұрыштары (4- графа) мына формула бойынша анықталады:

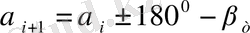(7)

мұндағы 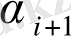және 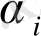- теодолиттік жүрістің ілгері, кейінгі жақтарының дирекциондық бұрыштары.
Есептеудің дұрыстығы 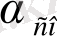бұрышын алу арқылы тексеріледі. Есептелінген дирекциондық бұрыштар 4-графаға толтырылады.
Румбтарды есептеу
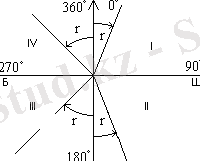
Кестен 3 пайдаланып, координаталар өсімшесінің таңбасы мен бағыттарын көрсету арқылы анықталған дирекциондық бұрыштарды румбтарға ауыстырады (сурет 9).

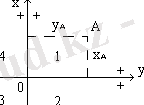
Сурет 9.

Кесте 1. - Дирекциондық бұрыштар мен румбтар арасындағы байланыс
Ширектер
Дирекциондық бұрыштардың өзгеруі
Румбтардың аттары
Байланыс формалары
I
II
III
IV
0°-тан 90°-қа
90°-тан 180°-қа
180°-тан 270°-қа
270°-тан 360°-қа
СШ
ОШ
ОБ
СБ
r1=α1
r2=180°-α2
r3=α3-180°
r4=360°-α4

Румбтардың мәнін бүтін минутқа дейін дөңгелектеп, координаталар ведомосінің 5-графасына жазады.

Сурет 10

Координаталар өсімшелерін есептеу
Координаталар өсімшелері (7, 8 графа) мына формуламен анықталады:

Δх = 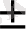d cosr (8)
Δy = d sinr

Дирекциондық бұрыш α-ның әртүрлі ширекте орналасуына сәйкес таңбаларының өзгеруi кесте 2 көрсетiлген.

Кесте 2. Координаталар өсімшелерінің ширектегі таңбалары
Координаталар өсімшелері
Ширектер

І-СШ
ІІ-ОШ
ІІІ-ОБ
ІV-СБ
Δх
+
-
-
+
Δу
+
+
-
-

Координаталар өсiмшелерi (8) формуласымен есептелiп, координаталар ведомосiнiң 7,8 -графаларына жазылады. Тригонометриялық функциялардың мәнiн үтiрден кейiн екі таңбалы санға дейін дөңгелектеп анықтайды.
Қиыспаушылықтар былай анықталады:

(9)

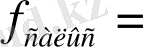
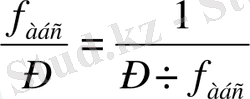(10)

мұндағы Р - теодолиттiк жүрiс қабырғаларының қосындысы.

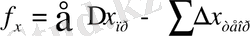
(11)

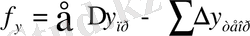
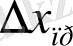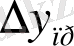;- өсімшелердің қосындысы.
Салыстырмалы қате мына шектен аспауы керек:

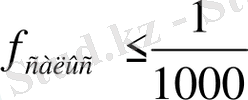
Өсімшелер қателері 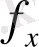пен 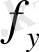шектен аспаса, оларды кері таңбамен жазық ара қашықтықтарға пропорционал етіп бөледі:

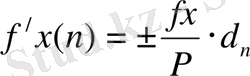
(12)

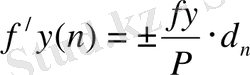
мұндағы 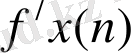, 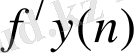- координаталар өсімшелерінің түзетулері.
Түзетілген координаталар өсімшелері координаталар ведомосінің 9, 10-графаларына жазылады.

Теодолиттiк жүрiс төбелерiнiң координаталарын есептеу

Теодолиттiк жүрiстер төбелерiнiң координаталары алдыңғы нүкте координаталарына келесi нүкте координаталарының өсiмшелерiн қосқанға тең болады. Нүктенiң координаталары мына формуламен анықталады:

Өлшен-ген(β)
Түзетіл-ген(β)
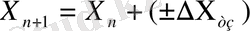
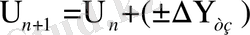
Дирек-ция(α)
41º33,6'
Румб(r)
Арақашық-тық(S)
Cos r
Sin r
Өлшенген
Түзетілген
Координаталар

Δх= s*cos r
Δу = s*sin r
Δх
Δу
Х
У
1
2
3
4
5
6
7
8
9
10
11
12
13
14
1
92º32,0'-3
92º31,7'
129º01,9'
51º1,9'
361,45
0,6267
0,7792
-226,53-0,1
+281,65+0,08
-226,63
+281,73
1000
1000
2
123º01,5'-3
123º01,2'
186º00,7'
6º00,7'
320,68
0,9945
0,1046
-318,91-0,1
-33,55+0,09
-319,01
-33,46
773,37
1281,7
3
129º32,5'-4
129º32,1'
236º28,6'
56º28,6'
235,24
0,555
0,8318
-130,56-0,15
-195,67+0,08
-130,71
-195,59
454,36
1248,2
4
95º03,0'-3
95º02,7'
321º25,9'
39º25,9'
200,00
0,7799
0,6258
+155,99-0,1
-125,16+0,08
+155,89
-125,08
323,65
1052,6
5
180º01,0'-3
180º00,7'
321º25,2'
39º25,2'
294,05
0,7799
0,6258
+229,33-0,1
-184,04+0,09
+229,23
-184,95
479,54
927,6
6
99º52,0'-4
99º51,6'
401º33,6'
41º33,6'
388,01
0,7508
0,6604
+291,33-0,1
+256,27+0,08
+291,23
+256,35
708,77
743,65
Тұйық жүріс:

∑βпрак=720º0,2' ∑+676,65 ∑+537,92 1000 1000
∑βтеор=720º0,0' ∑ - 676 ∑ - 538,42
0,656=0,1 - 0,56=0,08
Тұйықталмаған жүрісте бұрыштық қиылыспаушылығы ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.