Идеал газ моделі

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 13 бет
Таңдаулыға:

6-7. Дәріс тақырыбы

МОЛЕКУЛАЛЫҚ ФИЗИКА ЖӘНЕ ТЕРМОДИНАМИКА
6-7.1.ЗАТ ҚҰРЫЛЫСЫНЫҢ АТОМДЫҚ-МОЛЕКУЛАЛЫҚ ТЕОРИЯСЫ
Атомдық - молекулалық теория бойынша кез келген зат дербес бөлшектерден - атомдардан тұрады деген ұғым ертеден белгілі мәселе. М. Ломоносов атомдар мен молекулалардың үздіксіз жылулық қозғалыста екендігі туралы пікір айтқан. Сонымен, зат құрылысы туралы атомдық теория дүниеге келді. Бұл теория бойынша, материалдық дененің моделі белгілі бір заңмен өзара әсерлесетін және сол заңға сәйкес қозғалыста болатын атомдар мен молекулалардан тұрады. Зат мөлшері сол заттың структуралық элементтерінің санымен сипатталады. Ол мольң деген физикалық түсінікпен түсіндіріледі. Берілген элементтің грамм-атомы деп сол элементің граммен алынған массасы, сан жағынан оның атомдық массасына тең мөлшерін айтамыз. Кез келген элементтің грамм-атомдағы атомдардың (структуралық элементтерінің саны) саны бірдей болады. Бұл сан Авогадро саның деп аталады. Берілген элементтің грамм-молекуласы деп сол элементтің граммен алынған массасы сан жағынан оның молекулалық массасына тең болатын мөлшерін айтады. Кез келген заттың грамм-молекуласындағы молекулалар саны бірдей болады және ол Авогадро санына тең болады. Грамм-молекуланы көбінесе мольң деп атайды. Моль - берілген заттардың әрбірі үшін (әрқайсысы үшін) айрықша мәні бар масса бірлігі. Мысалы, сутегі молекуласы үшін (Н2): 1 моль сутегі 2-ге тең, себебі оның молекуласының массасы 2 атомдық өлшем бірлікке тең, яғни
mH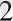=2∙()
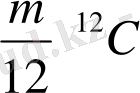тең. Сутегі молекуласының 2 грамм массасында, көміртегі молекуласының 12 грамм массасында, судың (H2O) молекуласының 18 грамм массасында, күкірт қышқылының (H2S O 4) 96 грамм массасында молекулалардың массасының саны бірдей болады, ол Авогадро санына тең болады. NA=Авогадро саны=6.023∙1023 . Авогадро санын білу, бізге микроәлемнің, яғни атом және молекула әлемінің масштабы жөнінде әлде қайда түсінікті ұғым береді. Мысалы, молекула санын біле отырып, біз молекулалардың өлшемділігін, олардың массаларының абсолют (граммен алынған массасын) және берілген массадағы молекулалар санын анықтай алатын боламыз. Айталық, 1 см3 су алайық, оның массасы 1 грамм болады, олай болса, ол су мөлшерінің 1 молін 118 бөлігіне тең болады екен. Массасы 1 грамм суда қанша молекула болады десек, ол былай анықталады:
NA= 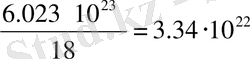молекула бар екен. Есептің берілген шарттарынан білеміз, судың 1 см3 көлемдегі молекула санын есептеп 1 молекула көлемін анықтаймыз, жуық шамамен
V0=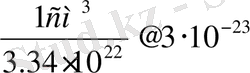см3
болады. Молекулалардың формасы (пішіні) шар тәрізді деп қарастырсақ, оның радиусы
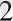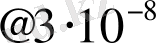rHOсм
Бір молекуланың массасын (m0) мына қатынастан анықтауға болады.
m0= немесе m0=
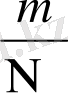
мұндағы μ - зат мөлшері (моль массасы); m - кез келген зат массасы; N - молекула саны
mH=1.675∙10-24г.
Бір молекуланың көлемін біле отырып, заттың 1 өлшем көлемінде қалыпты жағдайдағы (р=1 атм, Т=+273.15, V=1м3 немесе см3) молекулаларының санын есептеуге болады. Мысалы, 1см3 көлемдегі газ молекулаларының жалпы саны ~n2.7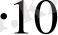19 молекула болады.
Идеал газ моделі
Көп бөлшектерден тұратын жүйелердің ең қарапайым моделі идеал газң деп аталады. Идеал газдың анықтамасы бойынша: нүктелік материялдың бөлшектерден тұратын, массасы нольге тең емес, араларында алыстан әсерлесу күштері жоқ және әсерлесулері тек бірімен бірі кездескенде ғана пайда болатын (әсерлесулері шарлардың соқтығысу заңына бағынатын) жүйе. Табиғатта мұндай газ болмайды, тек біз ойша осындай қасиеттері бар деп есептейміз. Осындай газдар үшін теория жүзінде болатын құбылыстар зерттеледі. Бірақ, тәжірибе кейбір нақты газдардың қасиеттері белгілі бір шарттар орындалғанда идеал газдардыңң қасиеттеріне ұқсас болады. Сол ұшін идеал газң заңдылықтары нақты газдар үшін пайдаланылады. Көп бөлшектерден тұратын жүйелерді зерттеу әдістері: динамикалық, статистикалық, термодинамикалық болып үшке бөлінеді. Макроскопиялық денелердің қасиеттерін зерттейтін физиканың бөлімін статикалық физика деп атайды, яғни бірдей және өте көп бөлшектерден тұратын (өте көп молекулалардан, атомдардан, электрондардан және т.б. бөлшектерден тұратын) жүйелерді зерттейтін бөлім. Зерттеулер осы макроскопиялық денені құраушы бөлшектердің қасиеттеріне және олардың өзара әсерлесуіне негізделіп жүргізіледі. Статикалық физика денелердің макроскопиялық теориясың деп те аталады. Макроскопиялық денелер қатарына қалыпты жағдайдағы (р0=1.013∙105Па, V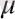=22.41∙10-3м3 Т0=273.15K) идеал газ жатады. Мысалы, температура 0˚С=273.15К деп және қысым 1.013∙105Па да идеал газдың 1 см3 көлемінде 2.7∙1019 молекула болады.
Статикалық физиканың бір бөлімі тепе-теңдіктегі статикалық термодинамикаң. Тепе-теңдіктегі статикалық термодинамика, термодинамикалық тепе-теңдіктегі процестердің заңдарын зерттейді, физикалық жүйенің термодинамикалық сипаттаушыларын есептейді және өзара әсерлесу заңдарына сүйеніп физикалық жүйе күйінің теңдеуін шығарады. Термодинамикалық тепе-теңдік күйдегі макроскопиялық физикалық жүйелердің жалпы түрдегі қасиеттерін және олардың бір күйден екінші күйге өту процестерін зерттейтін ғылым. Термодинамика термодинамика бастамасың деп аталатын көп жылғы бақылау нәтижесінде пайда болған денелер жүйесі туралы тұжырымдарға сүйеніп дүниеге келген. Термодинамиканың қолдану шегін статикалық физика анықтайды. Қатысты белгілеулер Газдардың күйін қысым p, көлем V және температура Т параметрлермен анықтауға болады. Бұл параметрлердің арасында өзара байланыстар бар, оларды жалпы түрде күйлер теңдеуі деп аталатын
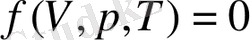. (6-7.1)
функциалды тәуелділікпен көрсетуге болады.
Бойль-Мариотт және Гей-Люссак заңдарын біріктіре отырып, идеал газ күйінің теңдеуін қорытылады.
Айталық газдың берілген массасының алғашқы күйінің параметрлері p1, V1, T1 болсын. Газбен қандай да бір процесс жүріп, оның соңғы күйінің параметрлері p2,V2,T2 болсын. (6-7.1-сурет.) 1 күйден 2-ші күйге газдың көшуі 1) изотермалық (1-1Ө изотермасы) 2) изохаралық (1Ө-2 изохаралық) екі процесс арқылы болсын. Бойль-Мариотт және Гей-Люссак заңдарына сәйкес
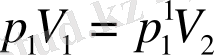, (6-7.2)
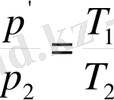. (6-7.3)
деп жазамыз. (6-7.2) өрнегінен р мәнін (6-7.3) - ге қойсақ, онда

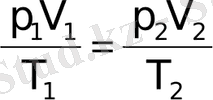
1 және 2 күйлер кез келген болғандықтан, берілген газ массасы үшін pVT тұрақты шама болады, яғни
, (6-7.4)
мұндағы В - әртүрлі газдар үшін әртүрлі тұрақты шама. (6-7.4) өрнегі Клапейрон теңдеуі деп аталады. Д.И. Менделеев Клапейрон теңдеуін Авогадро теңдеуімен біріктіріп, (6-7.4) теңдеуін, (молярлы көлем V ұғымын) пайдаланып бір моль газ үшін жазды. Авогадро заңы бойынша, барлық газдардың бір молінде р және Т бірдей болатындықтан молярлы көлем бірдей, сондықтан В барлық газдар үшін тұрақты шама, оны R мен белгілейміз, ол молярлы газ тұрақтысы деп аталады.
, (6-7.5)
Қалыпты жағдай үшін R-ді есептесек
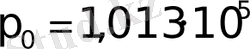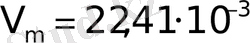Па, м[3], .
Cонда
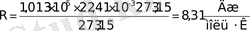. (6-7.6)
болады. Бір моль газ үшін жазылған (6-7.5) теңдеуден кез келген газ (m) массасына арналған теңдеуге көшуге болады. Ол үшін бірдей жағдайларда молі газының көлемі есе артық екендігін ескерсек, онда 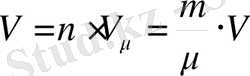. (6-7.5) өрнегіне 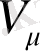орнына 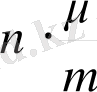-ді қойып мына өрнекті аламыз:
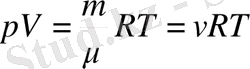(6-7.7)
мұндағы 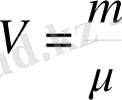-зат мөлшері. (6-7.7) теңдеуі кез келген масса үшін Клапейрон-Менделеев өрнегі деп аталады. Идеал газ күйі теңдеуінің басқаша түрі жиі пайдаланылады. Ол үшін Больцман тұрақтысын енгіземіз:

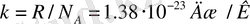
Осыған сәйкес (1.4) күй теңдеуін мына түрде жазамыз

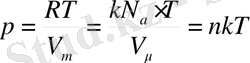
мұндағы NА 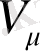=n - молекулалар концентрациясы (көлем бірлігіндегі саны). Сонымен,
(6-7.8)
Теңдеуінен: идеал газдың қысымы, берілген температура кезінде оның молекулалар концентрациясына немесе газ тығыздығына тура пропорционал болатындығы көрінеді. Бірдей температуралар және бірдей қысымдар кезінде барлық газдар бірлік көлем ішіндегі барлық молекулалар саны бірдей болады. Қалыпты жағдайдағы газдың 1м3 көлемінде құралатын молекулалар сандары Лошмидт саны деп аталады:

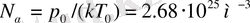
6-7.2.МОЛЕКУЛА-КИНЕТИКАЛЫҚ ТЕОРИЯ
Газдардың кинетикалық теориясы бойынша, бір атомды газдарды материялық нүктелер жүйесі деп қарастыруға болады. Газдың қысымы молекулаларының ыдыс қабырғасына түсіретін соқтығысулары арқылы анықталады. Ыдыс қабырғасына түсірілген (макроскопиялық параметр) Р қысым мен молекуланың (микросипаттамасын) массасы - m0, молекуланың концентрациясы - n, және оның жылдамдықтары - 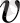араларындағы байланыстарды көрсететін өрнекті молекула-кинетикалық теорияның негізгі теңдеуің деп аталады. Осы газ туралы молекула-кинетикалық теорияның негізгі теңдеуін қорытып шығарамыз. Ол үшін газ молекулаларының тік бұрышты куб формалы ыдыстағы қозғалыстарын қарастырамыз. Қарастыру кезіндегі жүргізілетін түрлі есептерді жеңілдету мақсатымен кейбір қысқартулар жасаймыз. Мысалы, газ молекулаларының ретсіз қозғалысын, өзара перпендикуляр үш бағытта болады деп санаймыз және кез келген уақыт мезетінде кез келген үш бағыттың бір бағытына қарай барлық молекулалардың 13 бөлігі қозғалып барады деп жорамалдаймыз. Молекулалардың екі бүйір қабырғасының арасындағы қозғалысты қарастырсақ, ыдыстағы молекулалардың 16 бөлігі оң қабырғадан сол қабырғаға, енді бір бөлігі (16) сол қабырғадан оң қабырғаға қарай қозғалып барады деп қарастырайық. Куб тәрізді ыдыстың оң жақтағы қабырғасынан ΔS элементар ауданын бөліп алып және сол ауданға Δt уақыт аралығындағы молекулалардың соғылу (z) санын анықтайық. Осы Δt уақыт аралығында ΔS ауданға қабырғадан қашықтықта тұрған молекулалардың барлығы жететін болады. Соғылудың саны Z барлық молекулалардың 16 бөлігі суретте көрсетілген цилиндр ішіндегі молекулалар санымен анықталады.
, (6-7.9)
мұндағы n - молекулалар концентрациясы. Егер, молекула қабырғаға соғылуға дейін 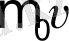импульсына ие болса, онда соғылу кезінде қабырғаға берген молекула импульсі мына өрнекпен анықталады.

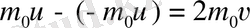
мұндағы m0- молекула массасы, 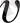- оның жылдамдығы. Бір қабырғаға түсетін толық импульс, молекулалар саны Z арқылы анықталады:
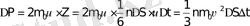. (6-7.10)
Ньютонның екінші заңы бойынша 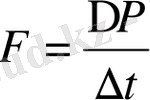. Қысым - ΔS аудан бірлігіне әсер ететін күш ретінде, яғни 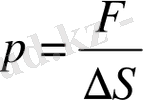. Сонымен (6-7.10) өрнектен қабырғаға түсетін газ молекулаларының қысымы:
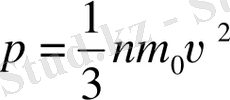. (6-7.11)
Айталық, V көлем ішінде υ1, υ 2,.., υ nжылдамдықтары болатын молекулалар болсын десек.
Бұл жағдайда, , (6-7.12)

орташа квадраттық жылдамдық ұғымы қарастырылады, бұл барлық молекулалардың жиынтығын сипаттайды.
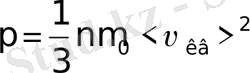(6-7.13)
Бұл өрнек идеал газдардың молекула - кинетикалық теориясының негізгі теңдеуі деп аталады. Егер, 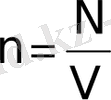деп молекулалар концентрациясы екендігін ескерсек, онда негізгі теңдеу мынадай түрге келеді:
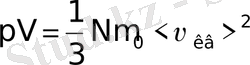немесе 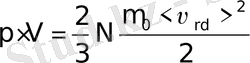(6-7.14)
мұндағы 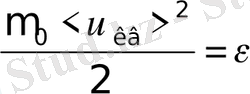- бір молекуланың энергиясы болғандықтан, онда барлық молекулалардың ілгерілемелі қозғалысының толық кинетикалық энергиясы 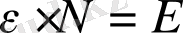болады.
Сонда 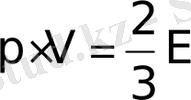. Газ массасы болғандықтан, (6-7.14) өрнегін келесі түрде жазуға болады
(6-7.15)
Бір моль газ үшін m=М (М-молярлы масса), сондықтан
(6-7.16)
мұндағы 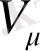- молярлы көлем. Екінші жағынан Клапейрон-Менделеев теңдеуі бойынша. 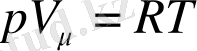. Онымен, 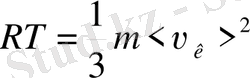. Осыдан 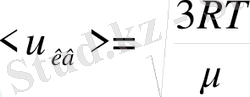,мұндағы 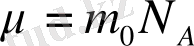болғандықтан
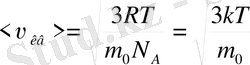, (6-7.17)
мұндағы k=RNA - Больцман тұрақтысы; NA-Авогадро заңы. Идеал газдың бір молекуласының ілгерілемелі қозғалысының кинетикалық энергиясы
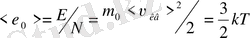(6-7.18)
Молекуланың ілгерлемелі қозғалысының орташа кинетикалық энергиясы тек температураға тәуелді болады. Егер Т=0 болса 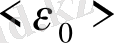=0 болады, яғни абсолют ноль температурада молекуланың ілгерлемелі қозғалысы тоқталады.Бізге (6-7.18) өрнегі температураны молекула-кинетикалық теория бойынша түсіндіру мүмкіндігін береді. Термодинамикалық температура идеал газ молекулаларының ілгерлемелі қозғалысының орташа кинетикалық энергиясының өлшемі.

6-7.3.СТАТИСТИКАЛЫҚ ТАРАЛУ
Сырттан күш әсер етпеген идеал газ молекулалары жылулық қозғалыстарының салдарынан өздері орналасқан көлемде бір келкі бөлініп орналасады. Сондықтан, тепе-теңдік күйде бір өлшем көлемдегі молекула саны n болады. Мұндай тепе-теңдік күйдегі газдың қысымы көлемнің кез келген нүктесінде бірдей болады және мынадай өрнекпен анықталады:
P=n∙k∙T
Егер, қарастырылып отырған газ сыртқы күш өрісіне орналастырылған болса, онда әрбір молекулаға сыртқы күш әсер ететін болады Бұл жағдай газ молекулаларының көлем бойынша орналасуының бірқалыпты болмауына әкеліп соғады. Осы жағдай газ қысымының әр түрлі болуына себеп болады. Қарастырылатын газ Жердің тартылыс өрісінде орналасқан десек, яғни Жердің потенциалдық өрісінде десек, газ молекулаларының жылулық қозғалысы және тартылыс әсерінен болатын қозғалыс газ күйінің әлде бір стационар күйде болуына әкеледі, ол күй бойынша Жер бетінен биіктеген сайын газ қысымының азайуына әкеледі. Қысымның биіктікке байланысты өзгеру заңын қорытып шығару кезінде, мынадай жорамал жасаймыз: Жердің тартылыс күшінің өрісі бірқалыпты, температура тұрақты және барлық молекулалардың массалары бірдей деп газ қысымын анықтаймыз.

Жылдамдықтар бойынша молекулалар таралуының Максвелл заңы
Молекула-кинетикалық ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.