Булев функцияларының жалған және елеулі айнымалыларын анықтау: теориялық негіздер мен Delphi ортасындағы программалық жүзеге асыру


Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 17 бет
Таңдаулыға:
Қазақстан Республикасы Білім және Ғылым министрлігі
Д. СЕРІКБАЕВ атындағы ШЫҒЫС ҚАЗАҚСТАН МЕМЛЕКЕТТІК
ТЕХНИКАЛЫҚ УНИВЕРСИТЕТІ
ФАКУЛЬТЕТІ: ИНФОРМАЦИОНДЫҚ ТЕХНОЛОГИЯ ЖӘНЕ
ЭНЕРГЕТИКА
КАФЕДРА: МАТЕМАТИКАЛЫҚ ЖӘНЕ КОМПЬЮТЕРЛІК
МОДЕРЛЕРЛЕУ
Тақырыбы: Буль математикасы
Орындаған: Ілияс Айсұлтан
Тобы: 11 ГДк-1
Қабылдаған: Нұрсадықова Р. Қ
Өскемен 2012
Мазмұны
Кіріспе . . . 3
Логика
Формулалардың эквиваленттігі. Қосалқылык принципі . . . 5
Буль функцияларын айнымалыларға жіктеу. Кемел дизъюнктивті нормаль қалып 6
Толықтық және тұйықтық . . . 7
Жегалкин теоремасы . . . 8
Маңызды жабық сыныптар. Толықтық туралы теорема . . . 9
Пост нәтижелері . . . 10
Буль функцияларының жалған және елеулі айнымалылары . . . 10
Буль функцияларының жалған және елеулі
айнымалыларын программада жүзеге асыру . . . 14
Қорытынды . . . 19
Қлданылған әдебиеттер тізімі . . . 20
Кіріспе
Жалпы алғанда буль функцияларының жалған және елеулі айнымалыларының дискреттік математикада ойнайтын рөлі өте зор. Бірінші оларды теориялық тұрғыдан қарастырайық. Буль функцияларының жалған және елеулі айнымалылары деп . . . атайды.
Бұл айнымалылардың маңызы өте зор. Мысалы, функция көп айнымалы болса, кейбір айнымалыларын (жалған айнымалыларды) алып тастауға болады. Ол бізге барлық параметрлер бойынша үнемдеуге мүмкіндік береді. Сондықтан осы үнемдеуді жүзеге асыратын программдық пакет құру актуалды мәселе. Бұл жұмыста қойылған мақсат бойынша бірінші теориялық, одан кейін программалық жүзеге асыру жүргізілді.
ЛОГИКА АЛГЕБРАСЫ
1. Логика алгебрасының функциялары
Айталық U-{u
1
, и
2
, . . . , и
m
, . . . }
-
айнымалылардың бастапқы алфавиті болсын. Аргументтері E
2
={О, 1} жиынында анықталған және а
i
∈Е
2
(і = 1, 2, . . . , n)
,
егер а
i
∈Е
2
(і = 1, 2, . . . , п) шартын қанағаттандыратын ƒ(u
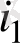 , u
, u
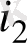 , …, u
, …, u
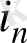 ) функциялары қарастырылады.
) функциялары қарастырылады.
Бұл функциялар логика алгебрасыныц функциялары немесе буль фунщиялары деп аталады. Р 2 арқылы U алфавитінде берілген, сондай-ақ 0 және 1 тұрақтыларын қамтитын барлық логика алгебрасының функциялар жүйесін белгілейміз.
Теорема . х 1 , х 2 , . . . , х n п айнымалыға тәуелді Р 2 жиынындағы барлық
функциялар саны
P
2
(n) -
2
2
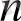 Equation. 3
-
ге тең.
Equation. 3
-
ге тең.
Логика алгебрасы функцияларың мысалдары:
- ƒ1(x) =0 -тұрақты 0
- ƒ2(x) =1-тұрақты 1;
- ƒ3(x) =x -тепе-тең функция;
- ƒ4(x) =- х -ті жоққа шығару;
- ƒ5(x1, x2) = (x1&x2) - x1мен x2-нің конъюнкциясы (логикалық көбейту) ;
- ƒ6(x1, x2) = (x1∨x2) - x1мен x2-нің дизъюнкциясы (логикальщ қосу) ;
- ƒ6(x1, x2) =Бұл функциялардың мәні.
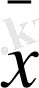
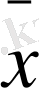
0 0
0 1
0
0
0
1
1
1
0
1
1
1
1
0
1
0
2. Формулалар. Формулаларды функциялармен жузеге асыру
Анықтама. Айталық β- Р 2 жиынындағы функциялар ішжиыны
болсын.
а) Индукция базисі. β ішжиынындағы әрбір ƒ (x 1 , …, x m ) функция β-ғы формула деп аталады.
b) Индуктивті өту. Айталық ƒ (x 1 , …, x m ) - β жиынындағы функция болсын және A 1 , …, A m -β жиынындағы формула немесе U жиынындағы айнымалылар символы болатын өрнек болсын. Онда ƒ (A 1 , . . . , А m ) өрнегі β жиынындагы формула деп аталады.
с) Формуланың индуктивті анықтамасына сүйене отырып, β-дағы әрбір F(х 1 , . . . , x n ) функциясына Р 2 жиынындағы ƒ (х 1 , . . . , x n ) функциясын сәйкес қоямыз.
d) Индукция базисі. Егер. F(х 1 , . . . , x n ) = ƒ (х 1 , . . . , x n ), мүндағы ƒ ∈β, онда F(х 1 , . . . , х n ) формуласына ƒ (х 1 , . . . , x n ) функциясын сәйкес қоямыз.
e) Индуктиві өту. Айталық F(х 1 , . . . , x n ) =ƒ (х 1 , . . . , x n ) мұндағы А i (і = 1, . . . , m) β-дағы формула немесе х j(i) айнымалысыньщ белгісі.
Онда индуктивті болжам бойьнша А i -ге Р г жиынындағы ƒ i
функциясы немесе ƒ =х j(i) тепе-тең функция сәйкес қойылған.
F(х 1 , . . . , x n ) формуласына ƒ (х 1 , . . . , x n ) = ƒ 0 (ƒ 1 , . . . , ƒ m ) функциясын сәйкес қоямыз.
Егер ƒ функциясы F формуласына сәйкес келсе, онда F формуласы ƒ функциясын жүзеге асырады дейді.
F формуласына сәйкес келетін ƒ функциясы β-дағы функциялардың суперпозициясы деп, ал ƒ функциясын β -дан алу үрдісі суперпозиция операциясы деп аталады.
3. Формулалардың эквиваленттігі. Қосалқылык принципі
Анықтама. F және G формулалары β жиынында эквивалентті деп аталады, егер оларға сәйкес функциялар тең болса: ƒ F = ƒ G .
(х 1 ◦х 2 ) арқылы (x 1 &x 2 ), (x 1 ∨x 2 ), (х 1 +х 2 ) функцияларының кез-келгенін белгілейік.
Логика алгебрасы фунщияларыныц цасиеттері
1) (x 1 ◦х 2 ) функциясы ассоциативтілік қасиетке ие:
((x 1 ◦x 2 ) ◦ x 3 ) = (x 1 ◦(x 2 ◦x 3 ) ) .
2) (х 1 ◦х 2 ) функциясы коммутативтілік қасиетке ие :
(x 1 ◦x 2 ) =(x 2 ◦x 1 )
3) Конъюнкция және дизъюнкция үшін дистрибутивтілік заң орындалады :
((x 1 ∨x 2 ) & x 3 ) = ((x 1 &x 3 ) ∨(x 2 &x 3 ) )
((x 1 &x 2 ) ∨ x 3 ) =((x 1 ∨x 2 ) &(x 2 ∨x 3 )
4)
 =
x,
=
x,
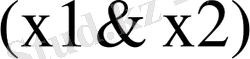 Equation. 3 =(
Equation. 3 =(
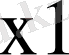 Equation. 3 ∨
Equation. 3 ∨
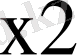 Equation. 3 ),
Equation. 3 ),
 Equation. 3 =(
Equation. 3 =(
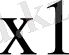 Equation. 3 &
Equation. 3 &
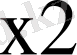 Equation. 3 )
Equation. 3 )
5) (x&
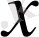 Equation. 3 ) =0, (x∨
Equation. 3 ) =0, (x∨
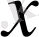 Equation. 3 ) =1,
Equation. 3 ) =1,
(x&0) =0, (x∨0) =x,
(x&1) =0, (x∨1) =x.
Анықтама.
[ƒ (х
1
, . . . , x
n
) ] *=
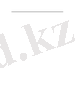 (
(
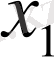 , …,
, …,
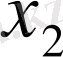 ) функциясы ƒ (х
1
, . . . , x
n
)
) функциясы ƒ (х
1
, . . . , x
n
)
функциясына қосалқы функция деп аталады.
- 0 функциясы 1 функцияға қосалқы,
- 1 функциясы 0 функциясына қосалқы,
- x функциясы х функциясына қосалқы,
- функциясыфункциясына қосалқы,
- х&х2функциясы х1vх2функциясына қосалқы,
x 1 v х 2 функциясы х 1 &х 2 функциясына қосалқы.
Қосалқылықтың анықтамасынан ƒ ** =( ƒ * ) * = ƒ екендігі шығады, яғни функция ƒ * функциясына қосалқы.
Қосалқылық принципі. Егер F=С[ƒ 1 , . . . , ƒ s ] формуласы ƒ (х 1 , . . . , x n )
функциясын жүзеге асырса, онда F формуласынан ƒ 1 , . . . , ƒ s функциясын
ƒ 1 * , . . . , ƒ s * функциясына ауыстыру аркылы алынған С[ƒ 1 * , . . . , ƒ s * ] формуласы, ƒ * (х,, . . . , х n ) функциясын жүзеге асырады.
Бұл формуланы F формуласына
қосалқы формула
деп атайды және F
*
арқылы белгілейді. Егер Ғ = С[0, 1,
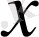 , х
1
&х
2
, (x
1
∨x
2
), онда F
*
=С[0, 1,
, х
1
&х
2
, (x
1
∨x
2
), онда F
*
=С[0, 1,
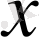 Equation. 3, (x
1
∨x
2
), x
1
&х
2
] .
Equation. 3, (x
1
∨x
2
), x
1
&х
2
] .
4. Буль функцияларын айнымалыларға жіктеу. Кемел дизъюнктивті нормаль қалып
х
 =хσ∨хσ белгілеуін енгізейік, мұндағы σ - нөлге немесе бірге тең параметр.
=хσ∨хσ белгілеуін енгізейік, мұндағы σ - нөлге немесе бірге тең параметр.
x
σ
=
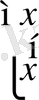
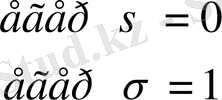
х σ = 1 тек сол жағдайда, егер х = σ болса екендігіне оңай көз жеткізуге болады.
Теорема
(Буль функцияларын айнымалыларға жіктеу туралы) . Әрбір ƒ(х
1
, . . . , x
n
) логика алгебрасының функциясын кез-келген
т(1
 т
т
 п)
үшін келесі түрде беруге болады :
п)
үшін келесі түрде беруге болады :
ƒ (х
1
, . . . , x
m
, x
m+1
, …, x
n
) =
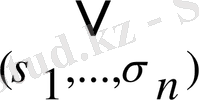 x
1
σ
1
&…& x
m
σ
m
ƒ(σ
1
, …, σ
m
, x
m+1
, …, x
n
),
x
1
σ
1
&…& x
m
σ
m
ƒ(σ
1
, …, σ
m
, x
m+1
, …, x
n
),
(*)
мұнда дизъюнкция х 1 , . . . , х m айньмалыларының барлық мүмкін болатын мәндері бойынша алынады.
Бұл көрініс функцияның х 1 , . . . , х m айнымалылары бойынша жіктелінуі деп аталады.
Салдар ретінде жіктеудің арнайы екі түрін аламыз.
Айнымалы бойынша жіктелу:
ƒ (х
1
, . . . , х
n-1
, х
n
) = х
n
& ƒ (x
1
, …, x
n-1
, 1)
v
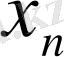 & ƒ(x
1
, …, x
n-1
, 0) .
& ƒ(x
1
, …, x
n-1
, 0) .
ƒ (х 1 , . ., х n-1 , 0) және ƒ(х 1 , . . . , x n-1 , 1) функциялары жіктеудің құрамдас бөліктері деп аталады.
- Барлық айньмалылар бойынша жіктеу:
ƒ (х 1 , . . . , x n ) =
x 1 σ 1 &…& x n σ n ƒ(σ 1 , …, σ n ) .
ƒ (х 1 , . . . , x n ) ≡0 орындалғанда жіктеу келесі түрге айналады
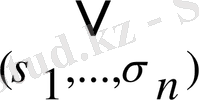 x
1
σ
1
&…& x
n
σ
n
ƒ(σ
1
, …, σ
n
) =
x
1
σ
1
&…& x
n
σ
n
ƒ(σ
1
, …, σ
n
) =
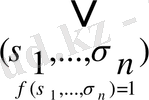 x
1
σ
1
&…& x
n
σ
n
x
1
σ
1
&…& x
n
σ
n
Нәтижесінде
ƒ (х
1
, . . . , x
n
) =
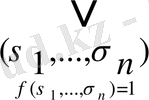 x
1
σ
1
&…& x
n
σ
n
x
1
σ
1
&…& x
n
σ
n
(**)
екендігін аламыз.
Мұндай жіктелу кемел дизъюнктивті нормалъ қалып деп аталады (кемел д. н. ф. ) .
Теорема . Логика алгебрасының әрбір функциясы жоққа шығару, конъюнщия және дизъюнкция арқылы формула түрінде өрнектеле алады. Мысал. x 1 v х 2 функциясының кемел д. н. ф. -ін табу керек болсын.
Функцияның мәні бірге тең болатын үш жинақ бар: (0, 1), (1, 0), (1, 1) . Сондықтан
x
1
v
x
2
= x
1
0
& x
2
1
v
x
1
1
& x
2
0
v
x
1
1
& x
2
1
=
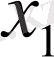 & x
1
v
x
1
&
& x
1
v
x
1
&
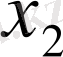 v
x
1
& x
2
.
v
x
1
& x
2
.
Конъюнктивті нормаль қалып деп аталатын жіктеуді аламыз (кемел к. н. ф. ) :
ƒ (х
1
, . . . , x
n
) =
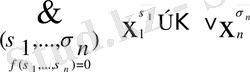
конъюнктивті нормаль калып деп аталатын жіктеуді аламыз (кемел к. н. ф. )
5. Толықтық және тұйықтық
Анықтама. Егер кез-келген Буль функциясы осы жүйенің функциялары арқылы формула түрінде жазылатын болса, онда Р 2 жиынындағы { f 1 , f 2 , …, f s , … }функциялар жүйесі толық деп аталады.
Толық жүйелердің мысалдары:
1. Р 2 жүйесі- барлық Буль функцияларынын жиыны -толық жүйе болып табылады.
2.
G
= {
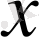 , x
1
& х
2
, x
1
vx
2
} жүйесі толық жүйе.
, x
1
& х
2
, x
1
vx
2
} жүйесі толық жүйе.
Кез-келген жүйе толық бола бермейді, мысалы G = {0, 1} жүйесі толық емес. Келесі теорема бір жүйенің толықтығын негізге ала отырып екінші жүйенің толықтығын анықтауға мүмкіндік береді.
Теорема. Айталық Р 2 жиынында екі функциялар жүйесі берілсін:
G={ f 1 , f 2 , … }, (I)
D={ g 1 , g 2 , … }, (II)
олар туралы мына жағдай белгілі: (I) жүйе толық және оның әрбір функциясы (II) жүйенің функциялары арқылы формула түрінде өрнектелген. Онда (II) жүйе толық.
Мысал:
D ={
, x 1 &x 2 } жүйесінің толық екендігін дәлелдеңіз.
Дәлелдеу: (I) жүйе ретінде 2 мысалдағы жүйені аламыз:
{
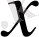 , x
1
& х
2
, x
1
vx
2
}, ал (II) жүйе ретінде - D жүйесін аламыз.
, x
1
& х
2
, x
1
vx
2
}, ал (II) жүйе ретінде - D жүйесін аламыз.
x
1
vx
2
=
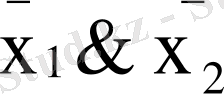 тепе-теңдігін пайдаланамыз (элементар функциялардың касиетінен) .
тепе-теңдігін пайдаланамыз (элементар функциялардың касиетінен) .
Сонымен, (I) жүйенің әрбір функциясы (II) жүйенің функциялары арқылы формула түрінде өрнектеледі. Яғни, (II) жүйе: {
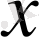 , х
1
&х
2
} толық жүйе болып табылады.
, х
1
&х
2
} толық жүйе болып табылады.
6. Жегалкин теоремасы.
Р
2
жиынындағы әрбір функция mod 2 бойынша көпмүшенің көмегімен өрнектеле алады (Жегалкин көпмүшесі бойынша) :
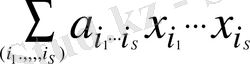
Мысал: (х 1 v х 2 ) функциясын Жегалкин көпмүшесі түрінде өрнектеңіз.
(x 1 vx 2 ) =ax 1 x 2 +bx 1 +cx 2 +d.
(0, 0) жинағында: x 1 =x 2 =0⇒0=a•0+b•0+c•0+d⇒d=0.
(0, 1) : x 1 =0, x 1 =1⇒1=a•0+b•0+c•1+d⇒c=1.
(1, 0) : x 1 =1, x 2 =0⇒1=a•0+b•1+c•0+d⇒b=1.
(1, 1) : x 1 =1, x 2 =1⇒1=a•1+b•1+c•1+d⇒a=1.
(x 1 vx 2 ) =x 1 x 2 +x 1 +x 2
Толықтық ұғымымен тұйықтау және тұйык сыныптар ұғымдары тығыз байланысты.
Анықтама. Айталық М- Р 2 жиынындағы функциялар ішжиыны болсын. М-нің тұйықтауы деп М жиынының функциялары арқылы формула түрінде беріле алатын барлық буль функцияларының жиыны аталады, [М] арқылы белгіленеді.
Мысал.
1) М = Р 2 . Бұл жағдайда [М] = Р 2 .
2) М = {1, х 1 +х 2 } . [М] - L барлық сызықты функциялар сыныбы:
f (х 1 , . . . , х в ) = с 0 +с 1 х 1 + . . . +с n x n , мұндағы с= 0, 1(i =0, . ., n), маңызды айнымалылар коэффициенті бірге тең де, жалған айнымалылар коэффициенті нөлге тең.
Тұйъқтаудыц қасиеттері
1) M⊆[M] .
2) [[M] ] =[M] .
3) егер М 1 ⊆М 2 , онда [М 1 ] ⊆[М 2 ] .
4) [M 1 ∪М 2 ] ⊇[М 1 ] ∪[М 2 ] .
Анықтама. М сыныбы (жиыны) тұйық деп аталады, егер [М] = М.
Мысал.
1) М = Р 2 сыныбы түйық сынып.
2) М = {1, x 1 + х 2 } сыныбы тұйық емес.
Толықтық анықтамасы бастапқыға эквивалентті : М - толық жүйе, егер [M] = Р 2 .
7. Маңызды жабық сыныптар. Толықтық туралы теорема.
Р 2 жиыньшдағы маңызды түйық сыныптарды қарастырайық.
1. T 0 арқылы барлық f (x 1 , …, x n ) буль функцияларының тұрақты нөлді сақтайтын сыныбын белгілейік, яғни f (0, . . . , 0) = 0 орындалатын функцияларды.
0, х, x 1 &х 2 , х 1 v х 2 , x 1 ⊕x 2 ∈T 0 ,
1,
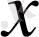 ∉T
0
.
∉T
0
.
Т 0 - тұйық сынып.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz